Aufgabe 3: Stochastik
3.1
Unter den Kunden eines Krankenversicherungsunternehmens haben  Datenschutzbedenken. Von den Kunden mit Datenschutzbedenken nutzen
Datenschutzbedenken. Von den Kunden mit Datenschutzbedenken nutzen  ein Fitnessarmband.
ein Fitnessarmband.  aller Kunden haben keine Datenschutzbedenken und nutzen ein Fitnessarmband.
aller Kunden haben keine Datenschutzbedenken und nutzen ein Fitnessarmband.
a)
Stelle den Sachverhalt in einem beschrifteten Baumdiagramm dar.
(3 BE)
b)
Eine unter allen Kunden zufällig ausgewählte Person nutzt ein Fitnessarmband.
Bestimme die Wahrscheinlichkeit dafür, dass sie Datenschutzbedenken hat.
Bestimme die Wahrscheinlichkeit dafür, dass sie Datenschutzbedenken hat.
(3 BE)
c)
Es gilt 
Begründe damit, dass die Ereignisse „Eine unter allen Kunden zufällig ausgewählte Person hat Datenschutzbedenken." und „Eine unter allen Kunden zufällig ausgewählte Person nutzt ein Fitnessarmband." stochastisch abhängig sind.
100 Kunden des Unternehmens werden zufällig ausgewählt.
Begründe damit, dass die Ereignisse „Eine unter allen Kunden zufällig ausgewählte Person hat Datenschutzbedenken." und „Eine unter allen Kunden zufällig ausgewählte Person nutzt ein Fitnessarmband." stochastisch abhängig sind.
(3 BE)
d)
Berechne die Wahrscheinlichkeit dafür, dass mehr als  der ausgewählten Kunden Datenschutzbedenken haben.
der ausgewählten Kunden Datenschutzbedenken haben.
(2 BE)
e)
Ersetzt man die Platzhalter  und
und  in geeigneter Weise, so kann mit dem Term
in geeigneter Weise, so kann mit dem Term  die Wahrscheinlichkeit eines Ereignisses im Sachzusammenhang berechnet werden.
die Wahrscheinlichkeit eines Ereignisses im Sachzusammenhang berechnet werden.
Gib an, wodurch die Platzhalter zu ersetzen sind, und beschreibe das zugehörige Ereignis.
Gib an, wodurch die Platzhalter zu ersetzen sind, und beschreibe das zugehörige Ereignis.
(3 BE)
f)
Berechne den Mindestumfang einer Stichprobe von Kunden, so dass in dieser mit einer Wahrscheinlichkeit von mindestens  mindestens eine Person Datenschutzbedenken hat.
mindestens eine Person Datenschutzbedenken hat.
(3 BE)
g)
Untersuche, ob es einen Wert von  mit
mit  gibt, für den die folgende Aussage richtig ist:
gibt, für den die folgende Aussage richtig ist:
-
Werden
(3 BE)
3.2
Ein Hersteller von Fitnessarmbändern möchte für die Angabe einer Qualitätsgarantie den Anteil fehlerhafter Fitnessarmbänder überprüfen. Der laufenden Produktion wird eine Stichprobe vom Umfang 240 entnommen.
Die Auswertung des Stichprobenergebnisses erfolgt mithilfe des abgebildeten Graphen, indem eine der Grenzen eines Prognoseintervalls für den unbekannten Anteil fehlerhafter Fitnessarmbänder in der Stichprobe zu einer Sicherheitswahrscheinlichkeit  ermittelt wird.
ermittelt wird.
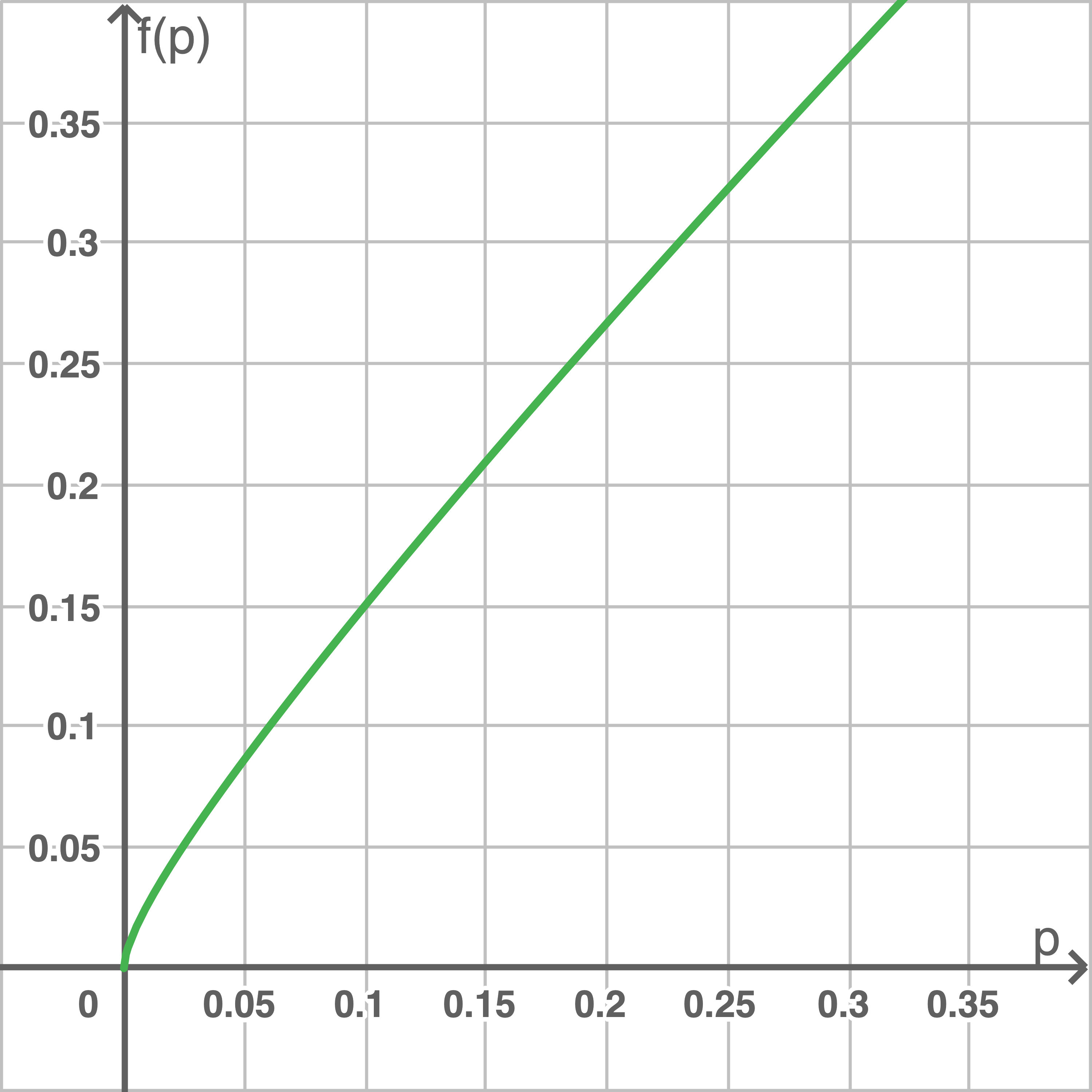
Für einen Wert  ist der Graph der Funktion
ist der Graph der Funktion  mit
mit
 und
und ![\(p\in [0;1]\)](https://mathjax.schullv.de/8e374375d1d438c760a2c38184939f72fa220d9c623797fcc44369db2643ff31?color=5a5a5a) dargestellt.
dargestellt.

a)
Ermittle mithilfe der Abbildung den Wert  und gib eine mögliche Sicherheitswahrscheinlichkeit
und gib eine mögliche Sicherheitswahrscheinlichkeit  an.
an.
(3 BE)
b)
Erläutere die Bedeutung der bei der Auswertung des Stichprobenergebnisses betrachteten Grenze des Prognoseintervalls.
(2 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
3.1
a)
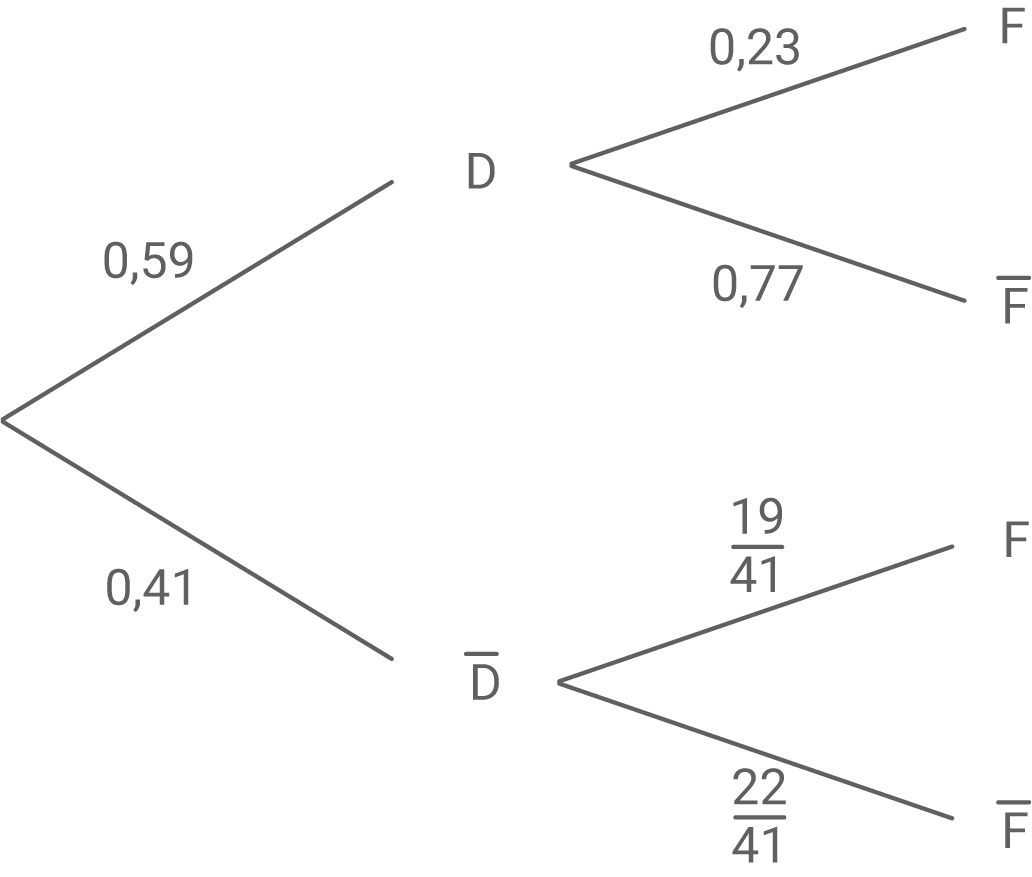
b)
Mit dem Satz von Bayes folgt:


c)
Da unter den Versicherten mit Datenschutzbedenken  ein Fitnessarmband nutzen, folgt
ein Fitnessarmband nutzen, folgt 
Der Term beschreibt den Anteil der Versicherten, die ein Fitnessarmband nutzen, unter allen Versicherten; also folgt
beschreibt den Anteil der Versicherten, die ein Fitnessarmband nutzen, unter allen Versicherten; also folgt 
Daher ist Somit sind die Ereignisse
Somit sind die Ereignisse  und
und  stochastisch abhängig.
stochastisch abhängig.
Der Term
Daher ist
d)
e)
Ein Vergleich mit der Formel für die Wahrscheinlichkeiten der Binomialverteilung ergibt:
Für  und
und  ist das zugehörige Ereignis „Höchstens die Hälfte der ausgewählten Versicherten hat Datenschutzbedenken."
ist das zugehörige Ereignis „Höchstens die Hälfte der ausgewählten Versicherten hat Datenschutzbedenken."
f)
Gegeben ist eine Binomialverteilung mit unbekanntem  und mit
und mit  . Ebenfalls ist das Ereignis
. Ebenfalls ist das Ereignis  gegeben.
Es gilt:
gegeben.
Es gilt:
 Es folgt:
Es folgt:
![\(\begin{array}[t]{rll}
1-P_{n;0,59}(X=0)&\geq& 0,98 &\quad \scriptsize \mid\; -1 \\[5pt]
-P_{n;0,59}(X=0) &\geq & -0,02 &\quad \scriptsize \mid\; \cdot (-1) \\[5pt]
P_{n;0,59}(X=0)&\leq& 0,02
\end{array}\)](https://mathjax.schullv.de/6b16ff186f21a8047da058c5b834e8dd73dd2e4630831ea9717aace90ee1b8d4?color=5a5a5a) Für
Für  ergibt sich
ergibt sich  und für
und für 
 Somit muss der Mindestumfang einer Stichprobe von Kunden bei
Somit muss der Mindestumfang einer Stichprobe von Kunden bei  liegen.
liegen.
g)
Es wird die folgende Situation beschrieben:
Da  gilt, hat die Gleichung keine Lösung, womit es keinen Wert von
gilt, hat die Gleichung keine Lösung, womit es keinen Wert von  gibt, mit welchem die Aussage richtig ist.
gibt, mit welchem die Aussage richtig ist.
3.2
a)
Aus der Abbildung kann  abgelesen werden. Somit folgt:
Mit Hilfe der Sigma Regeln erhält man die Sicherheitswahrscheinlichkeit zu
abgelesen werden. Somit folgt:
Mit Hilfe der Sigma Regeln erhält man die Sicherheitswahrscheinlichkeit zu 
b)
Die dargestellte Grenze entspricht der oberen Grenzen des Prognoseintervalls für den unbekannten Anteil fehlerhafter Fitnessarmbänder.
Ist der Anteil der fehlerhaften Armbändert in der Stichprobe größer als die betrachtete Grenze, so muss davon ausgegangen werden, dass die ursprünglich angenommene Wahrscheinlichkeit  eigentlich größer ist.
eigentlich größer ist.