Wahlpflichtaufgabe 1 - Analysis
4.1
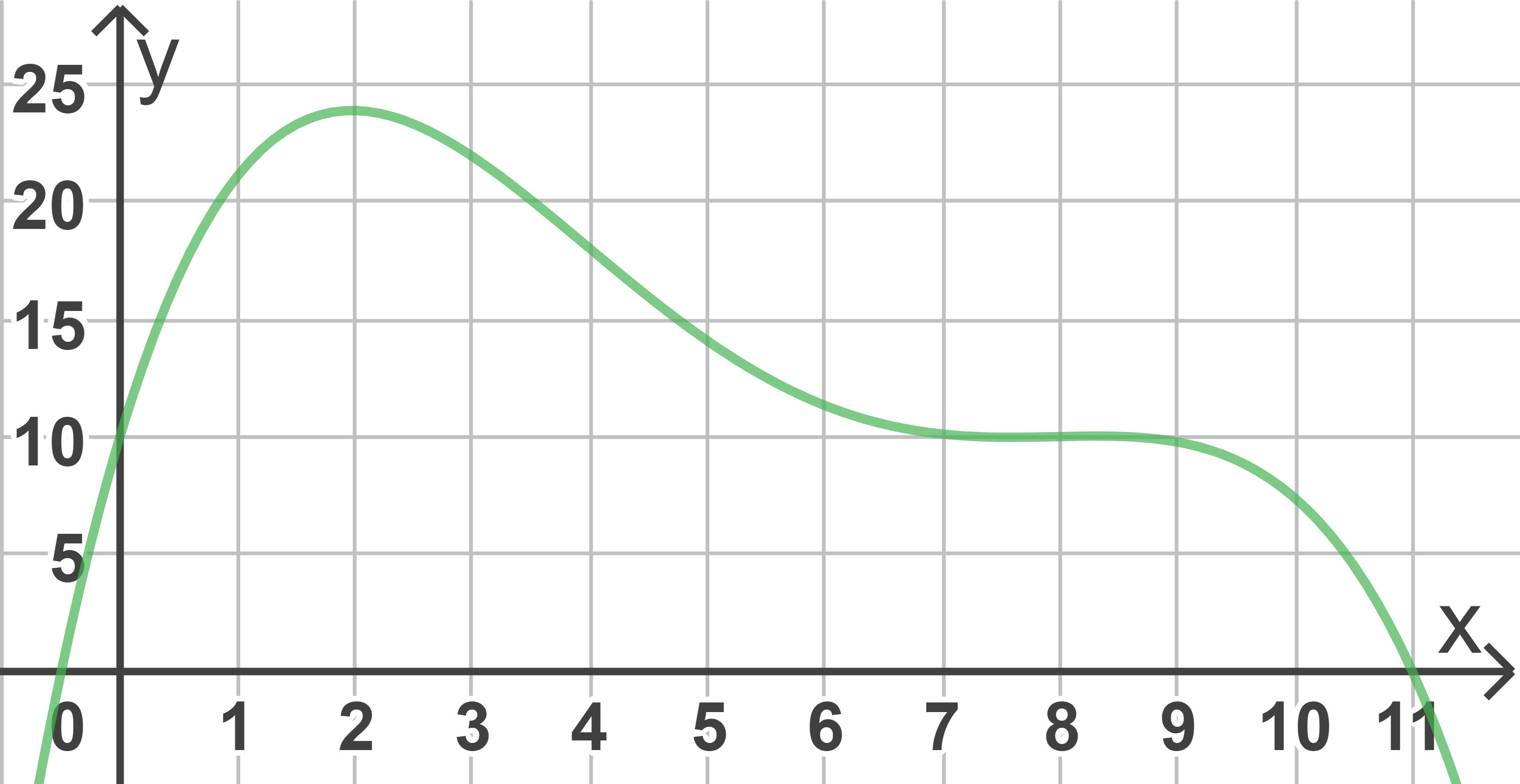
Die Abbildung zeigt den Graphen einer in 
definierten ganzrationalen Funktion 
vierten Grades. Die Tangente im Wendepunkt 
des Graphen hat die Steigung 
a)
Zeichne die beschriebene Tangente in die Abbildung ein und berechne die Größe des Winkels, unter dem diese Tangente die 
-Achse schneidet.
(3 BE)
b)
Begründe, dass der Graph von außerhalb des abgebildeten Bereichs keine Wendepunkte besitzt.
(2 BE)
c)
Gib die beiden Nullstellen der ersten Ableitungsfunktion 
von an.
(2 BE)
d)
Der Graph von hat einen Tiefpunkt. Gib die Koordinaten dieses Tiefpunkts an und begründe deine Angabe.
(3 BE)
e)
Deute den Wert des Terms 
geometrisch.
(2 BE)
f)
Beurteile die folgende Aussage:
Für jede Stammfunktion 
von gilt 
für jeden Wert von ![\(x\in[0;5].\)](https://mathjax.schullv.de/26a5be3c0e536f83dc20a89ef986c015a5d3ac58d0c085363f74f220eb732bf4?color=5a5a5a)
(3 BE)
4.1
a)
b)
Aus der Aufgabenstellung geht hervor, dass die Funktion den Grad 4 hat. Die zweite Ableitung 
der Funktion vierten Grades ist eine Funktion zweiten Grades. Eine Funktion zweiten Grades kann höchstens zwei Nullstellen annehmen. Dies sind dann die Wendestellen der Funktion .
Die zweite Ableitung nimmt den Wert Null, mit 
, an den Stellen 
und 
an. An der Stelle 
liegt ein Sattelpunkt.
Somit hat die zweite Ableitungsfunktion keine weitere Nullstelle und deshalb hat die Funktion keine weitere Wendestelle.
Somit hat die zweite Ableitungsfunktion
c)
Die Nullstellen der Ableitungsfunktion sind die Extremstellen der Funktion bzw. die Stellen, an der die Funktion keine Steigung hat. Diese liegen bei 
und .
d)
Eine Extremstelle der ersten Ableitung ist eine Nullstelle der zweiten Ableitung. Mit den Nullstellen der zweiten Ableitung berechnest du die Wendestellen der Funktion.
Die Koordinaten des Wendepunktes des Graphen von lauten 
. Die Wendestelle des Graphen von entspicht der Extremstelle des Graphen von . Es handelt sich um einen Tiefpunkt, da die Funktion im Bereich der Wendestelle monoton fällt.
Die Koordinaten des Wendepunktes des Graphen von
e)
Der Wert von 
stellt die Hälfte des Flächeninhalts dar, den der Graph von und die x-Achse im Intervall ![\([0 ; 2]\)](https://mathjax.schullv.de/b397e6702378a78dc30b1aa169a908bbe1f3c1e578fd08018963998620212206?color=5a5a5a)
einschließen.
ist eine Stammfunktion von 
Der Flächeninhalt den der Graph von mit der x-Achse einschließt entspricht der Summe der Funktionswerte von im Intervall ![\([0;2].\)](https://mathjax.schullv.de/9f001e7a68d1db871d8f573e1477bd4c3a21c6b1fecf3e2c5b0f4e947417ade8?color=5a5a5a)
Der Term gibt also den durchschnittlichen Funktionswert von im Intervall ![\([0;2]\)](https://mathjax.schullv.de/843d839ab55e0f672f243636b5611ab923c075cc63ed4cbee0bdb8f535440b7a?color=5a5a5a)
an.
Der Term
f)
Der Wert von 
stellt den Flächeninhalt dar, den der Graph von und die x-Achse im Intervall ![\([x; x+2]\)](https://mathjax.schullv.de/d200776b9f38d5e895ed01d4b5372466bc377ac82e418d19284988fb3325ee9e?color=5a5a5a)
einschließen.
Jede Fläche, die der Graph von mit der x-Achse im Intervall ![\([x; \; x+2]\)](https://mathjax.schullv.de/e6428c7b5c145925ae9232f463ddfee9b13279ada1e22a55b3a71f9d9338621d?color=5a5a5a)
einschließt, beinhaltet also mindestens ein Rechteck der Seitenlänge 2.
Die Höhe eines solchen Rechtecks, beträgt mindestens 10, denn für 
nimmt den kleinsten Funktionswert 
im Intervall ![\([x;x+2]\)](https://mathjax.schullv.de/f6b70ae8a63628b7b36bda74b355c3930b0d938342401a503b81bf80de67c28d?color=5a5a5a)
an.
Dieses Rechteck hat dann den Flächeninhalt 
.
Jedoch ist die Fläche, den der Graph von und die x-Achse im Intervall an 
einschließen etwas größer.
Es wird nämlich nicht nur ein Rechteck betrachtet, sondern die Fläche, die an den Verlauf des Graphens angrenzt. Somit ist die Aussage richtig. Um es dir noch besser zu verdeutlichen, kannst du dir diese Abbildungen ansehen.
Es wird nämlich nicht nur ein Rechteck betrachtet, sondern die Fläche, die an den Verlauf des Graphens angrenzt. Somit ist die Aussage richtig. Um es dir noch besser zu verdeutlichen, kannst du dir diese Abbildungen ansehen.