Mathematik Abi 2023: Aufgaben und Lösungen zu Funktionen und Wahrscheinlichkeiten

Die Abbildung zeigt den Graphen der in $\mathbb{R}$ definierten Funktion $f,$ dessen einzige Extrempunkte $(-1 \mid 1)$ und $(0 \mid 0)$ sind, sowie den Punkt $P.$

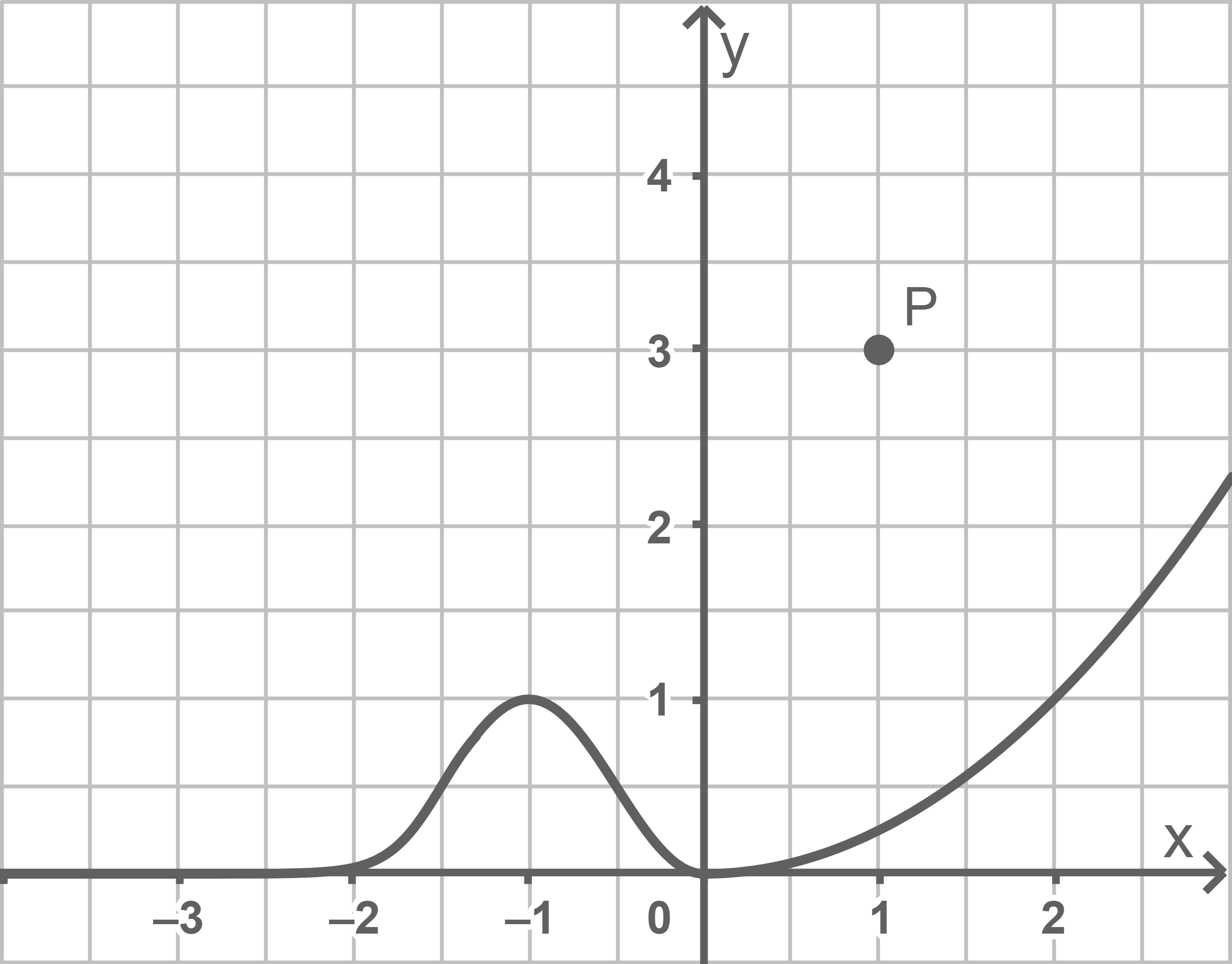
a)

Gib die Koordinaten des Tiefpunkts des Graphen der in $\mathbb{R}$ definierten Funktion $g$ mit $g(x)=-f(x-3)$ an.

(2 BE)

b)

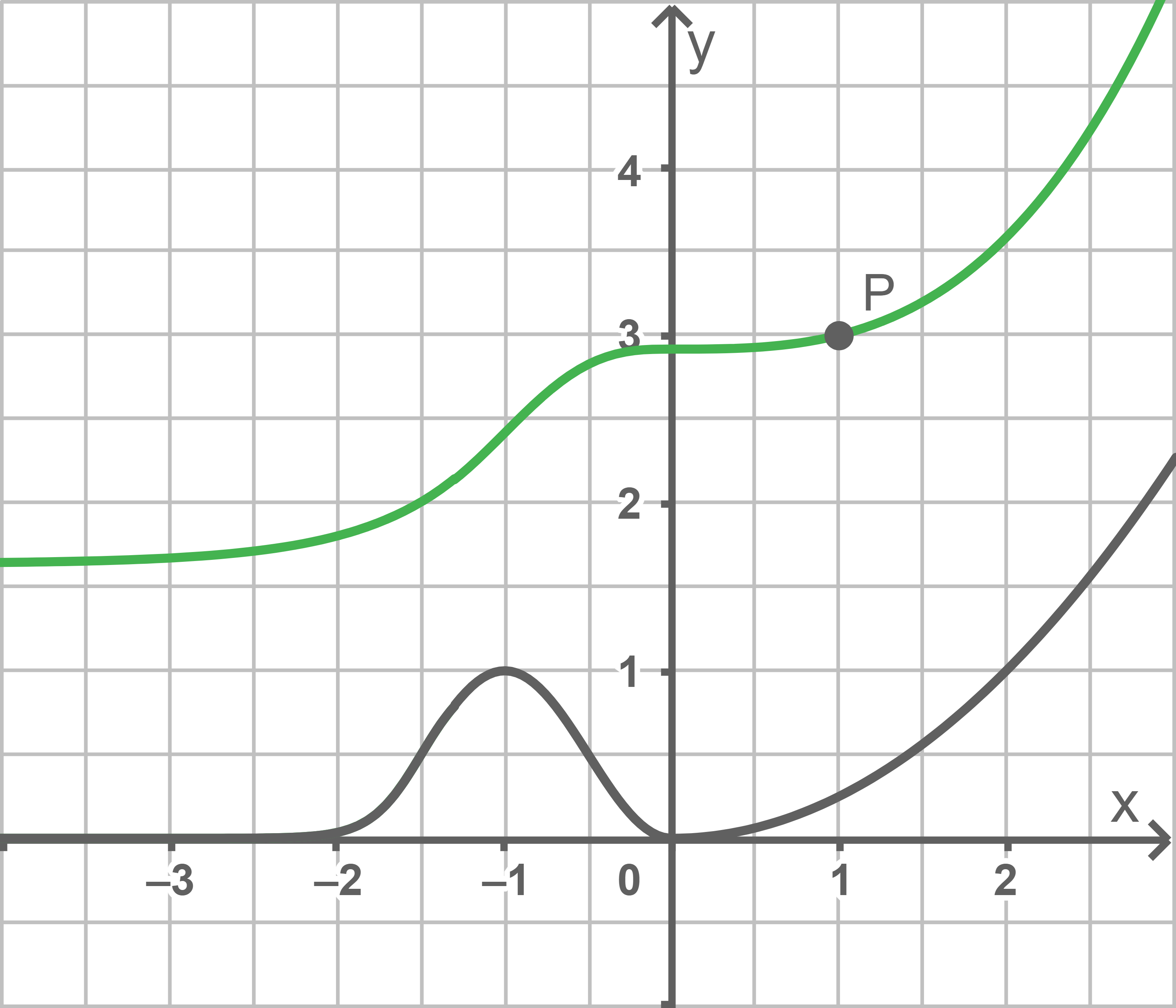
Der Graph einer Stammfunktion von $f$ verläuft durch $P.$

Skizziere diesen Graphen in der Abbildung.

(3 BE)

Gegeben sind die Geraden $g: \overrightarrow{x}=\pmatrix{1\\1\\1}+r\cdot \pmatrix{1\\2\\0}$ und $h: \overrightarrow{x}=\pmatrix{1\\1\\1}+s\cdot \pmatrix{2\\1\\0}$ mit $r, s \in \mathbb{R}.$

a)

Begründe, dass $g$ und $h$ nicht identisch sind.

(1 BE)

b)

Die Gerade $g$ soll durch Spiegelung an einer Ebene auf die Gerade $h$ abgebildet werden.

Bestimme eine Gleichung einer geeigneten Ebene und erläutere dein Vorgehen.

(4 BE)

In einen leeren Behälter werden drei Kugeln gelegt. Dabei wird die Farbe jeder Kugel durch Werfen eines Würfels festgelegt, dessen Seiten mit den Zahlen 1 bis 6 durchnummeriert sind:

Wird die „1" oder die „2" erzielt, wird eine gelbe Kugel gewählt, sonst eine schwarze.

a)

Weise rechnerisch nach, dass die Wahrscheinlichkeit dafür, dass sich nun mindestens zwei schwarze Kugeln im Behälter befinden, $\dfrac{20}{27}$ beträgt.

(2 BE)

b)

Aus dem Behälter werden zwei der drei Kugeln zufällig entnommen.

Ermittle die Wahrscheinlichkeit dafür, dass beide entnommenen Kugeln schwarz sind.

(3 BE)