Aufgabe 1: Analysis
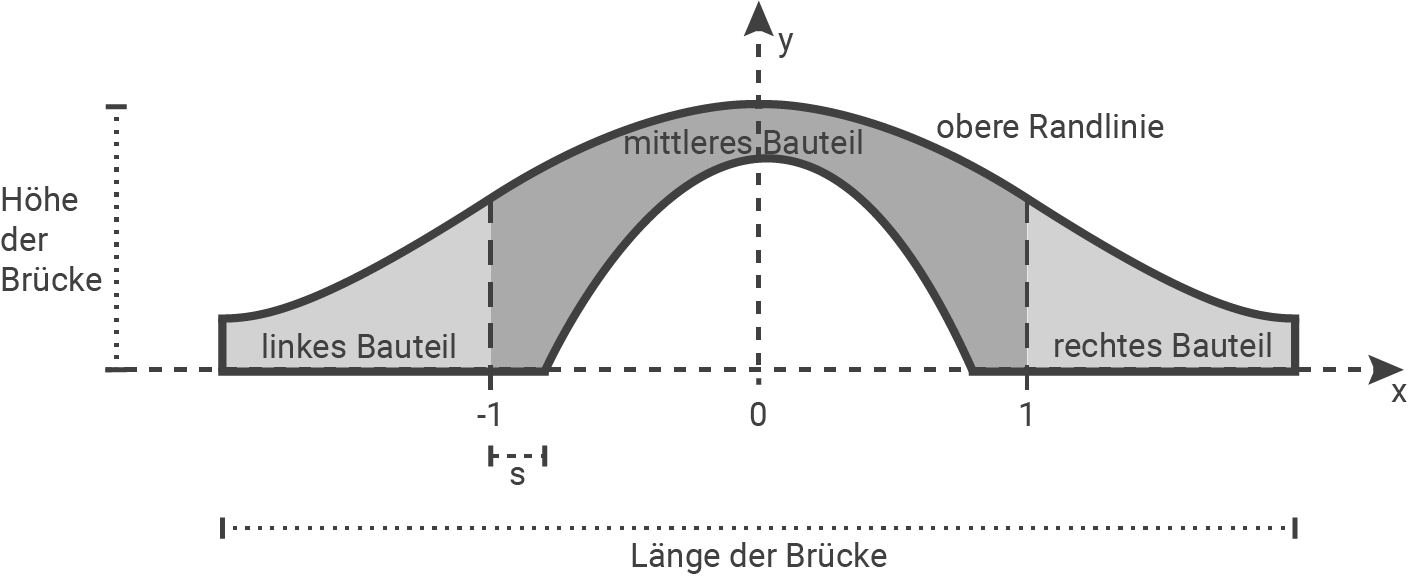
Die Abbildung 1 zeigt modellhaft den Längsschnitt einer dreiteiligen Brücke aus Holz für eine Spielzeugeisenbahn. Die Züge können sowohl über die Brücke fahren als auch darunter hindurch.
Die obere Randlinie des Längsschnitts der Brücke kann mithilfe des Graphen der in 
definierten Funktion 
mit 
beschrieben werden. Dabei werden die Endpunkte dieser Randlinie durch die beiden Tiefpunkte des Graphen von dargestellt. Im verwendeten Koordinatensystem beschreibt die x-Achse die Horizontale; eine Längeneinheit entspricht einem Dezimeter in der Realität.
definierten Funktion 
mit 
und 
, 
, beschrieben werden.
1.1
a)
Zeige rechnerisch, dass die obere Randlinie achsensymmetrisch ist.
(2 BE)
b)
Bestimme rechnerisch die Höhe und die Länge der Brücke.
[zur Kontrolle: Ein Tiefpunkt des Graphen von hat die x-Koordinate 2]
[zur Kontrolle: Ein Tiefpunkt des Graphen von
(5 BE)
c)
Betrachtet wird derjenige Punkt der oberen Randlinie, der sich am Übergang vom mittleren zum rechten Bauteil befindet. Prüfe, ob dieser Punkt auf halber Höhe zwischen dem höchsten Punkt der oberen Randlinie und deren rechtem Endpunkt liegt.
(3 BE)
d)
Gib die Bedeutung des Terms 
im Sachzusammenhang an und berechne seinen Wert.
(3 BE)
e)
Berechne die Größe des größten Steigungswinkels der Brücke, der beim Überfahren zu überwinden ist.
Der parabelförmige Teil der unteren Randlinie des Längsschnitts der Brücke kann mithilfe des Graphen einer in
(5 BE)
f)
In der Abbildung 1 ist die Länge einer der beiden Bodenflächen des mittleren Bauteils mit 
bezeichnet. Bestimme alle Werte von 
, die für diese Länge mindestens 0,1 dm liefern.
(4 BE)
g)
Begründe im Sachzusammenhang, dass für die Beschreibung der unteren Randlinie beliebig große Werte von nicht infrage kommen.
(3 BE)
h)
Für die Brücke gilt 
. Die drei Bauteile der Brücke werden aus massivem Holz hergestellt; 1 dm
des Holzes hat eine Masse von 800 Gramm. Die Brücke ist 0,4 dm breit.
Ermittle die Masse des mittleren Bauteils.
Ermittle die Masse des mittleren Bauteils.
(7 BE)
1.2
Während der Planung der Brückenform kamen zur Beschreibung der oberen Randlinie für das linke Bauteil eine Funktion 
und für das rechte Bauteil eine Funktion 
infrage. Auch bei Verwendung dieser Funktionen wäre die obere Randlinie achsensymmetrisch gewesen. Beurteile jede der folgenden Aussagen:
für 
für 
I
II
(4 BE)
1.3
Die Form und die Größe der Brücke werden verändert, indem im bisher verwendeten Modell die obere Randlinie des Längsschnitts mithilfe der in definierten Funktion 
mit
beschrieben wird.
Die Bauteile der veränderten Brücke lassen sich nach dem in Abbildung 2 dargestellten Prinzip aus einem quaderförmigen Holzblock sägen. Der beim Sägen auftretende Materialverlust soll im Folgenden vernachlässigt werden.
Der Graph von ist symmetrisch bezüglich jedes seiner Wendepunkte.
Ermittle mithilfe des Funktionsterms von den Flächeninhalt der gesamten in der Abbildung 2 gezeigten rechteckigen Vorderseite des Holzblocks.
(4 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
Der höchste Punkt der oberen Randlinie liegt in 
Höhe. Für den rechten Endpunkt gilt:
Die halbe Höhe zwischen dem höchsten Punkt der oberen Randlinie und dem rechten Endpunkt beträgt:
Der Punkt der oberen Randlinie, der sich am Übergang vom mittleren zum rechten Bauteil befindet, liegt also nicht auf halber Höhe zwischen dem höchsten Punkt der oberen Randlinie und deren rechtem Endpunkt.
Es gilt:
Notwendige Bedingung für Wendestellen anwenden:
![\(\begin{array}[t]{rll}
k](https://mathjax.schullv.de/2f04461007eb8472acead2891eb965a25e70ed4d9a11e03cea352b34a04235ab?color=5a5a5a)
Eine Wendestelle des Graphen von liegt bei 
Auf die hinreichende Bedingung kann aufgrund der Aufgabenstellung verzichtet werden.
Insgesamt können sechs Wendestellen aus der Abbildung abgelesen werden.
Die Länge des Holzblocks folgt mit 
Damit ergibt sich für den Flächeninhalt in Quadratdezimetern ![\(1,5 \cdot 6 \cdot 2 \cdot k(1,5) = 14,4\,[\text{dm}^2].\)](https://mathjax.schullv.de/8d333914efce5b9e6734a9c86cec36fdb8d0360581bf4ed495b504b28fbd0f2f?color=5a5a5a)
a)
Die obere Randlinie wird durch die Funktion beschrieben.
Der Graph von ist also achsensymmetrisch und somit auch die obere Randlinie.
b)
Höhe der Brücke
Der höchste Punkt der Brücke liegt in der Mitte.
Die Brücke ist also hoch.
Länge der Brücke
Die Länge der Brücke ist durch die Lage der Tiefpunkte des Graphen von definiert.
Notwendiges Kriterium für Extremstellen anwenden, um die
-Koordinaten der Tiefpunkte zu bestimmen:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/93a15fe2da2fd3482c204533a9930f4f3459e510a7db5ffcc9000c78b08b9a3a?color=5a5a5a)
Wegen des Satzes vom Nullprodukt ist diese Gleichung erfüllt, wenn 
oder 
ist.
![\(\begin{array}[t]{rll}
\frac{1}{5}x^2-\frac{4}{5} &=& 0 &\quad \scriptsize \mid\; + \frac{4}{5} \\[5pt]
\frac{1}{5}x^2 &=& \frac{4}{5} &\quad \scriptsize \mid\; \cdot 5\\[5pt]
x^2 &=& 4 \\[5pt]
x_{2/3} &=& \pm 2
\end{array}\)](https://mathjax.schullv.de/94c3f99a9a13ed438fc640d8f6140bcd08c6957da326ea15ab22e91eeb7a2401?color=5a5a5a)
Daraus ergibt sich in Verbindung mit der Abbildung des Aufgabenblattes, dass die Tiefpunkte des Graphen von die -Koordinaten 
und 
haben. Die Brücke ist also 
lang.
Notwendiges Kriterium für Extremstellen anwenden, um die
c)
d)
Der Term gibt die mittlere Steigung der oberen Randlinie des rechten Bauteils an.
e)
Die größte Steigung befindet sich in einem Wendepunkt.
Anwenden des notwendigen Kriteriums für Wendestellen:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/33268cd2220241556260ef95ac5fef6820272d23fc1f1f422bd98136002ecee4?color=5a5a5a)
Da die Steigung an der Stelle 
positiv und an der Stelle 
negativ ist, wird betrachtet. Für den Steigungswinkel an dieser Stelle folgt:
![\(\begin{array}[t]{rll}
\tan \alpha &=& f](https://mathjax.schullv.de/186a5f04b243027a9d2c34703166612b42ec39d5032e39dd6bd7d8f5ef2c8199?color=5a5a5a)
Der größte Steigungswinkel, der beim Überfahren der Brücke zu überwinden ist, ist ca. 
groß.
Anwenden des notwendigen Kriteriums für Wendestellen:
f)
Das linke Bauteil ist lang, die gesamte Brücke ist lang. ist mindestens 
wenn die Beträge der Nullstellen von höchstens 
betragen.
Für die Nullstellen von gilt:
Es muss also gelten:
![\(\begin{array}[t]{rll}
\sqrt{\frac{0,8}{a}} &\leq & 0,9 &\quad \scriptsize \mid\;()^2 \\[5pt]
\frac{0,8}{a} &\leq& 0,81 &\quad \scriptsize \mid\; \cdot a \gt 0 \\[5pt]
0,8 &\leq & 0,81a &\quad \scriptsize \mid\; : 0,81 \\[5pt]
\frac{80}{81} &\leq& a
\end{array}\)](https://mathjax.schullv.de/c1ee174c73c9cece64652b2e0d3dfd15363ec5cfc2c2a0beabd44538eaa9a0bf?color=5a5a5a)
Für 
beträgt die Länge mindestens 
Für die Nullstellen von
g)
Je größer der Wert von ist, desto schmaler ist der Graph von und damit die Durchfahrt der Brücke. Wird der Wert von zu groß, kann kein Zug mehr hindurchfahren.
h)
1. Begrenzung der unteren Randlinie des Längsschnitts des mittleren Bauteils bestimmen
Die untere Randlinie verläuft also innerhalb des Intervalls ![\([-0,8; 0,8].\)](https://mathjax.schullv.de/b39fc3ac32fe864c563b1712f052382c14ad81dd3b6daaaf3d1c242195da52ce?color=5a5a5a)
2. Flächeninhalt des Längsschnitts des mittleren Bauteils bestimmen
3. Volumen
4. Masse
Das mittlere Bauteil hat eine Masse von 288 Gramm.
1.2
I)
Diejenigen Teile der Graphen von und 
die im Längsschnitt die oberen Randlinien des linken bzw. rechten Bauteils darstellen, liegen nicht symmetrisch bezüglich des Koordinatenursprungs. Damit ist die Aussage falsch.
II)
Diejenigen Teile der Graphen von und die im Längsschnitt die oberen Randlinien des linken bzw. rechten Bauteils darstellen, liegen symmetrisch bezüglich der 
-Achse. Also gilt 
für 
und damit 
für 
Folglich ist die Aussage richtig.
1.3
Es gilt: