Aufgabe 1: Analysis
1.1
Auf einer Autobahn entsteht morgens an einer Baustelle häufig ein Stau, der sich dann wieder vollständig auflöst.
 Für die erste Ableitungsfunktion von
Für die erste Ableitungsfunktion von  gilt
gilt 
 die in
die in  definierte Funktion
definierte Funktion  mit
von Bedeutung.
mit
von Bedeutung.
 Um 07:30 Uhr hat der Stau eine bestimmte Länge. Es gibt einen anderen Zeitpunkt, zu dem der Stau die gleiche Länge hat.
Markiere diesen Zeitpunkt in der Abbildung 2, begründe deine Markierung und veranschauliche deine Begründung in der Abbildung 2.
Um 07:30 Uhr hat der Stau eine bestimmte Länge. Es gibt einen anderen Zeitpunkt, zu dem der Stau die gleiche Länge hat.
Markiere diesen Zeitpunkt in der Abbildung 2, begründe deine Markierung und veranschauliche deine Begründung in der Abbildung 2.
An einem bestimmten Tag entsteht der Stau um 6:00 Uhr und löst sich um 10:00 Uhr vollständig auf. Für diesen Tag kann die momentane Änderungsrate der Staulänge mit Hilfe der in  definierten Funktion
definierten Funktion  mit
beschrieben werden.
Dabei gibt
mit
beschrieben werden.
Dabei gibt  die nach 06:00 Uhr vergangene Zeit in Stunden und
die nach 06:00 Uhr vergangene Zeit in Stunden und  die momentane Änderungsrate der Staulänge in Kilometer pro Stunde an.
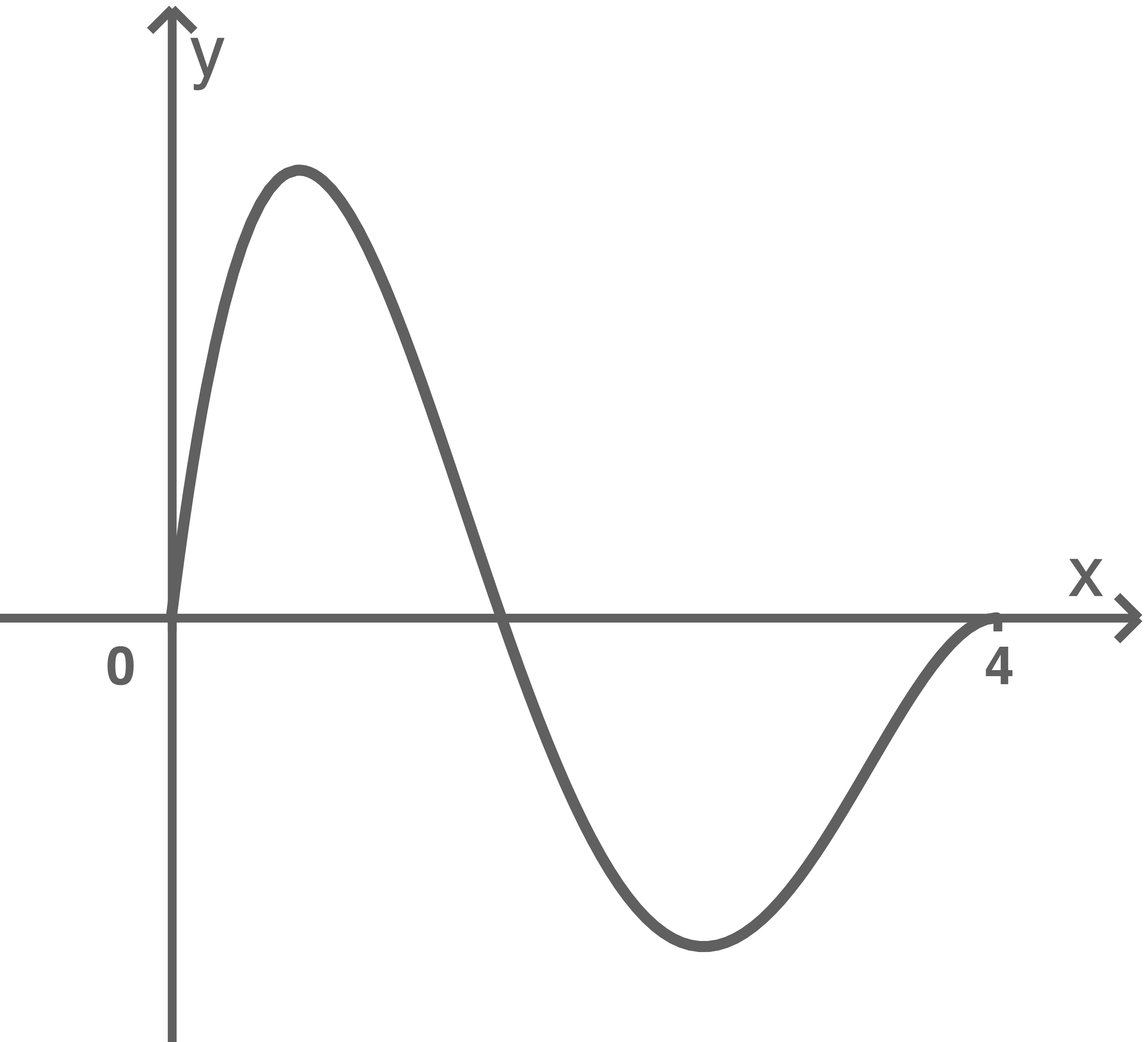
Die Abbildung 1 zeigt den Graphen von
die momentane Änderungsrate der Staulänge in Kilometer pro Stunde an.
Die Abbildung 1 zeigt den Graphen von  für
für  .
.

Abbildung 1
a)
Nenne die Zeitpunkte, zu denen die momentane Änderungsrate der Staulänge den Wert null hat, und begründe anhand der Struktur des Funktionsterms von  dass es keine weiteren solchen Zeitpunkte gibt.
dass es keine weiteren solchen Zeitpunkte gibt.
(3 BE)
b)
Es gilt  Gib die Bedeutung dieser Tatsache im Sachzusammenhang an.
Gib die Bedeutung dieser Tatsache im Sachzusammenhang an.
(1 BE)
c)
Bestimme rechnerisch den Zeitpunkt, zu dem die Staulänge am stärksten zunimmt.
(5 BE)
d)
Gib den Zeitpunkt an, zu dem der Stau am längsten ist.
Begründe deine Angabe.
Im Sachzusammenhang ist neben der Funktion
(2 BE)
e)
Begründe, dass die folgende Aussage richtig ist:
Die Staulänge kann für jeden Zeitpunkt von 06:00 Uhr bis 10:00 Uhr durch die Funktion  angegeben werden.
Bestätige rechnerisch, dass sich der Stau um 10:00 Uhr vollständig aufgelöst hat.
angegeben werden.
Bestätige rechnerisch, dass sich der Stau um 10:00 Uhr vollständig aufgelöst hat.
(4 BE)
f)
Berechne die Zunahme der Staulänge von 06:30 Uhr bis 08:00 Uhr und bestimme für diesen Zeitraum die durchschnittliche Änderungsrate der Staulänge.
(3 BE)
g)
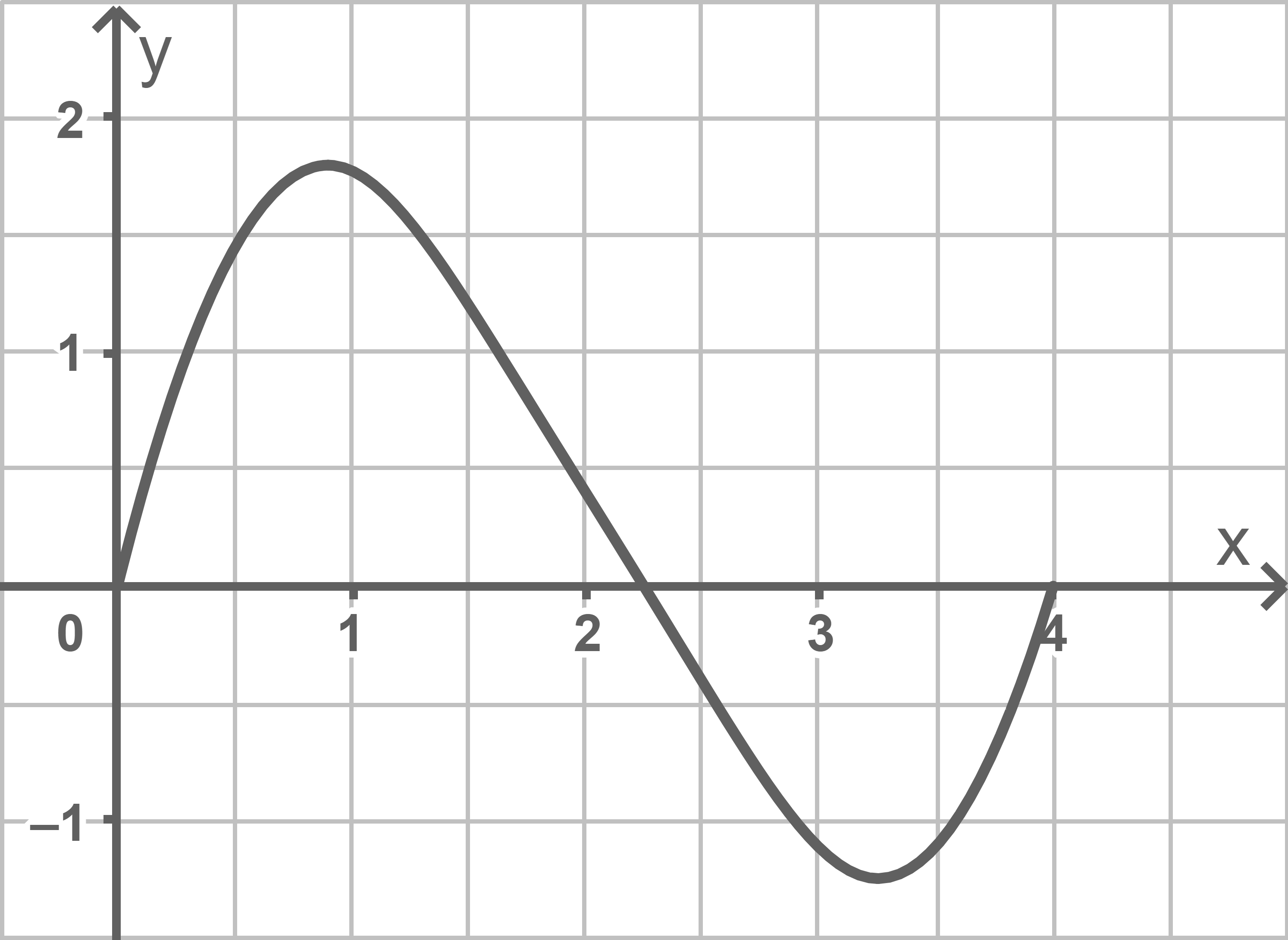
Für einen anderen Tag wird die momentane Änderungsrate der Staulänge für den Zeitraum von 06:00 Uhr bis 10:00 Uhr durch den in der Abbildung 2 gezeigten Graphen dargestellt.
Dabei ist  die nach 06:00 Uhr vergangene Zeit in Stunden und
die nach 06:00 Uhr vergangene Zeit in Stunden und  die momentane Änderungsrate der Staulänge in Kilometer pro Stunde.
die momentane Änderungsrate der Staulänge in Kilometer pro Stunde.

Abbildung 2
1.2
Betrachtet wird die Schar der in  definierten Funktionen
definierten Funktionen  mit
mit  und
und 
a)
Gib in Abhängigkeit von  das Verhalten von
das Verhalten von  für
für  an und begründe deine Angabe.
an und begründe deine Angabe.
(3 BE)
b)
Ermittle die Koordinaten der beiden Punkte, die alle Graphen der Schar gemeinsam haben.
(3 BE)
c)
Die erste Ableitungsfunktion von  wird mit
wird mit  bezeichnet.
Beurteile die folgende Aussage:
bezeichnet.
Beurteile die folgende Aussage:
Es gibt genau einen Wert von  für den der Graph von
für den der Graph von  Tangente an den Graphen von
Tangente an den Graphen von  ist.
ist.
(6 BE)
d)
Die Graphen von  und
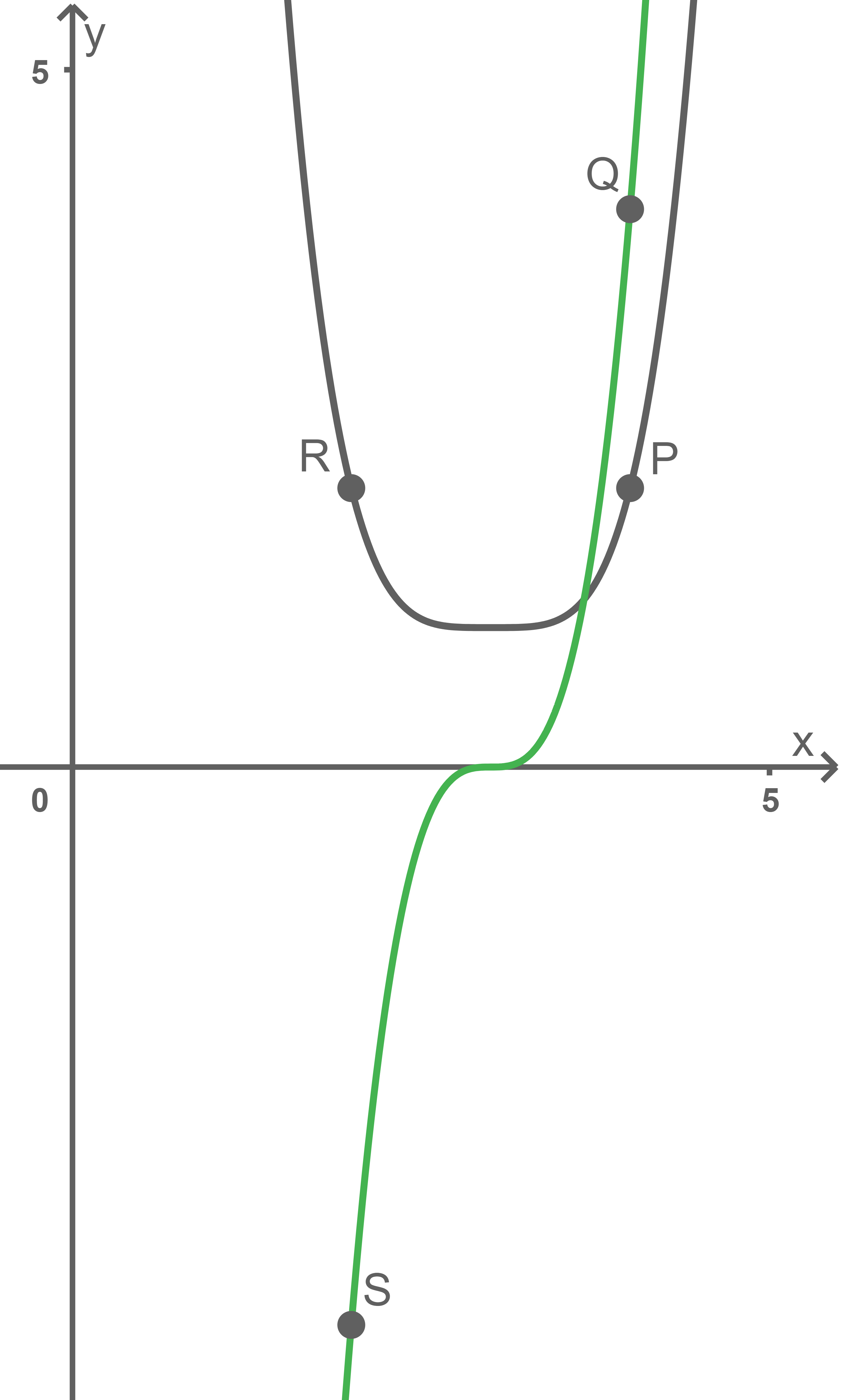
und  werden in der Abbildung 3 für
werden in der Abbildung 3 für  beispielhaft für gerade Werte von
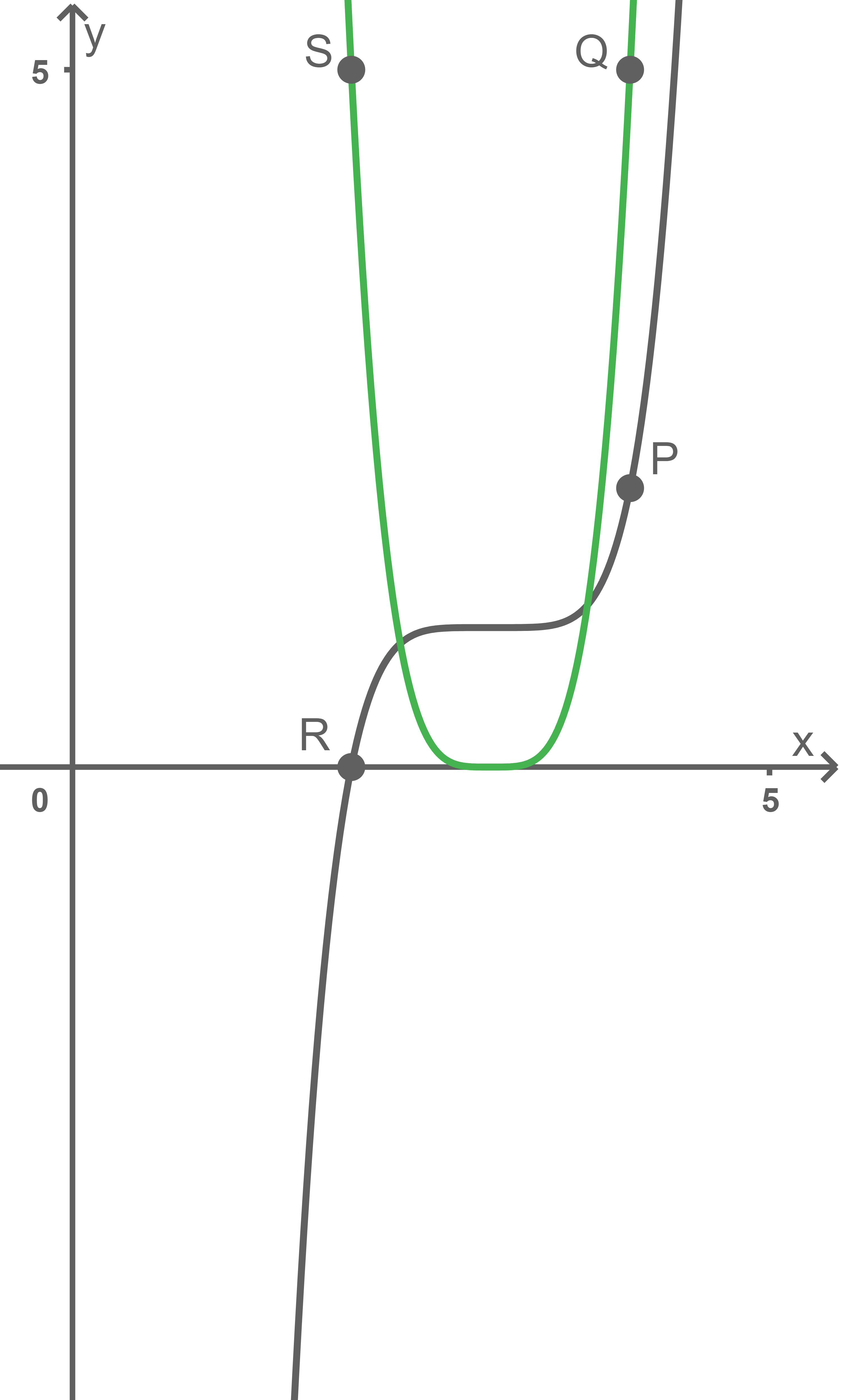
beispielhaft für gerade Werte von  gezeigt, in der Abbildung 4 für
gezeigt, in der Abbildung 4 für  beispielhaft für ungerade Werte von
beispielhaft für ungerade Werte von 
 Für
Für  werden die Punkte
werden die Punkte 

 und
und  betrachtet.
Diese Punkte sind jeweils Eckpunkte eines Vierecks.
Begründe, dass jedes dieser Vierecke ein Trapez ist, und zeige, dass die folgende Aussage richtig ist:
betrachtet.
Diese Punkte sind jeweils Eckpunkte eines Vierecks.
Begründe, dass jedes dieser Vierecke ein Trapez ist, und zeige, dass die folgende Aussage richtig ist:

Abbildung 3

Abbildung 4
Für jeden geraden Wert von  mit
mit  stimmen der Flächeninhalt des Trapezes für
stimmen der Flächeninhalt des Trapezes für  und der Flächeninhalt des Trapezes für
und der Flächeninhalt des Trapezes für  überein.
überein.
(7 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
a)
Zeitpunkte nennen
Es soll gelten:
![\(\begin{array}[t]{rll}
f(x)&=& 0&\\[5pt]
x \cdot(8-5 x) \cdot\left(1-\dfrac{x}{4}\right)\cdot \left(1-\dfrac{x}{4}\right) &=& 0
\end{array}\)](https://mathjax.schullv.de/9cfaac726503066242bdb9b8eef604d822753ccf929a84d28458f66b843fc7b1?color=5a5a5a) Mit dem Satz vom Nullprodukt folgt für die vier Linearfaktoren des Funktionsterms:
Mit dem Satz vom Nullprodukt folgt für die vier Linearfaktoren des Funktionsterms:

 und
und  Dies entspricht den Zeitpunkten 06:00 Uhr, 07:36 Uhr und 10:00 Uhr.
Der Funktionsterm von
Dies entspricht den Zeitpunkten 06:00 Uhr, 07:36 Uhr und 10:00 Uhr.
Der Funktionsterm von  besteht aus vier Linearfaktoren, von denen zwei übereinstimmen. Damit kann
besteht aus vier Linearfaktoren, von denen zwei übereinstimmen. Damit kann  maximal drei Nullstellen besitzen und es gibt daher nur die oben genannten drei Zeitpunkte, zu denen die momentane Änderungsrate der Staulänge den Wert null hat.
maximal drei Nullstellen besitzen und es gibt daher nur die oben genannten drei Zeitpunkte, zu denen die momentane Änderungsrate der Staulänge den Wert null hat.
b)
Um 08:00 Uhr nimmt die Staulänge ab.
c)
Notwendige Bedingung für Extremstellen anwenden:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/5478fb2450d2a2336a081f8ad46a75c817cbe9cb3f7a0a3e25494e32edbdd6dd?color=5a5a5a) Mit dem Satz vom Nullprodukt folgt:
Mit dem Satz vom Nullprodukt folgt:
![\(\begin{array}[t]{rll}
1-\dfrac{x_0}{4}&=& 0 &\quad \scriptsize \mid\; +\dfrac{x}{4} \quad \scriptsize \mid\;\cdot4 \\[5pt]
4&=& x_0
\end{array}\)](https://mathjax.schullv.de/200b501258f610bd0b4350e242c19b142524f28cb0f816320c51f7837fecf4be?color=5a5a5a) Außerdem gilt:
Außerdem gilt:
![\(\begin{array}[t]{rll}
5 x^2-16 x+8&=&0 &\quad \scriptsize \mid\;:5 \\[5pt]
x^2-\dfrac{16}{5} x+\dfrac{8}{5}&=&0 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/103174cab372bc943ff891d48ee24b44c739a1be4ad06b44a9f6570ff150cbef?color=5a5a5a) Die
Die  -Formel liefert nun:
-Formel liefert nun:
![\(\begin{array}[t]{rll}
x_{1;2}&=&\dfrac{8}{5}\pm\sqrt{\left(-\dfrac{8}{5}\right)^2-\dfrac{8}{5}} \\[5pt]
x_{1;2}&=&\dfrac{8}{5}\pm\sqrt{\dfrac{24}{25}} \\[5pt]
x_{1}&\approx& 0,62 \\[5pt]
x_{2}&\approx& 2,58
\end{array}\)](https://mathjax.schullv.de/7aaa68fd4dda82055d3556a563dabb4268f507089881c6b6293689365f6efabe?color=5a5a5a) Aus dem Verlauf der Abbildung ergibt sich, dass die Zunahme der Staulänge zum Zeitpunkt
Aus dem Verlauf der Abbildung ergibt sich, dass die Zunahme der Staulänge zum Zeitpunkt  am stärksten ist.
Für diesen Zeitpunkt gilt:
am stärksten ist.
Für diesen Zeitpunkt gilt:
![\(x_{1}\cdot 60 = 0,62\cdot 60 = 37,2\;[\text{min}]\)](https://mathjax.schullv.de/6fff5470e8817b557994f7fa72b0ea6668129b1cc49e529e60ee42a8d0087355?color=5a5a5a) Die Staulänge nimmt somit um ca.
Die Staulänge nimmt somit um ca.  am stärksten zu.
am stärksten zu.
d)
Die Länge des Staus nimmt genau dann zu, wenn  gilt.
Damit ist der Stau um 07:36 Uhr am längsten.
gilt.
Damit ist der Stau um 07:36 Uhr am längsten.
e)
Aussage begründen
Es gilt  und
und  Zeitpunkt der Auflösung bestätigen
Um 10:00 Uhr beträgt die Staulänge somit
Zeitpunkt der Auflösung bestätigen
Um 10:00 Uhr beträgt die Staulänge somit  Der Stau ist folglich aufgelöst.
Der Stau ist folglich aufgelöst.
f)
Zunahme berechnen
Die Zunahme der Staulänge beträgt somit  Durchschnittliche Änderungsrate bestimmen
Die Änderungsrate ergibt sich mit:
Durchschnittliche Änderungsrate bestimmen
Die Änderungsrate ergibt sich mit:

g)
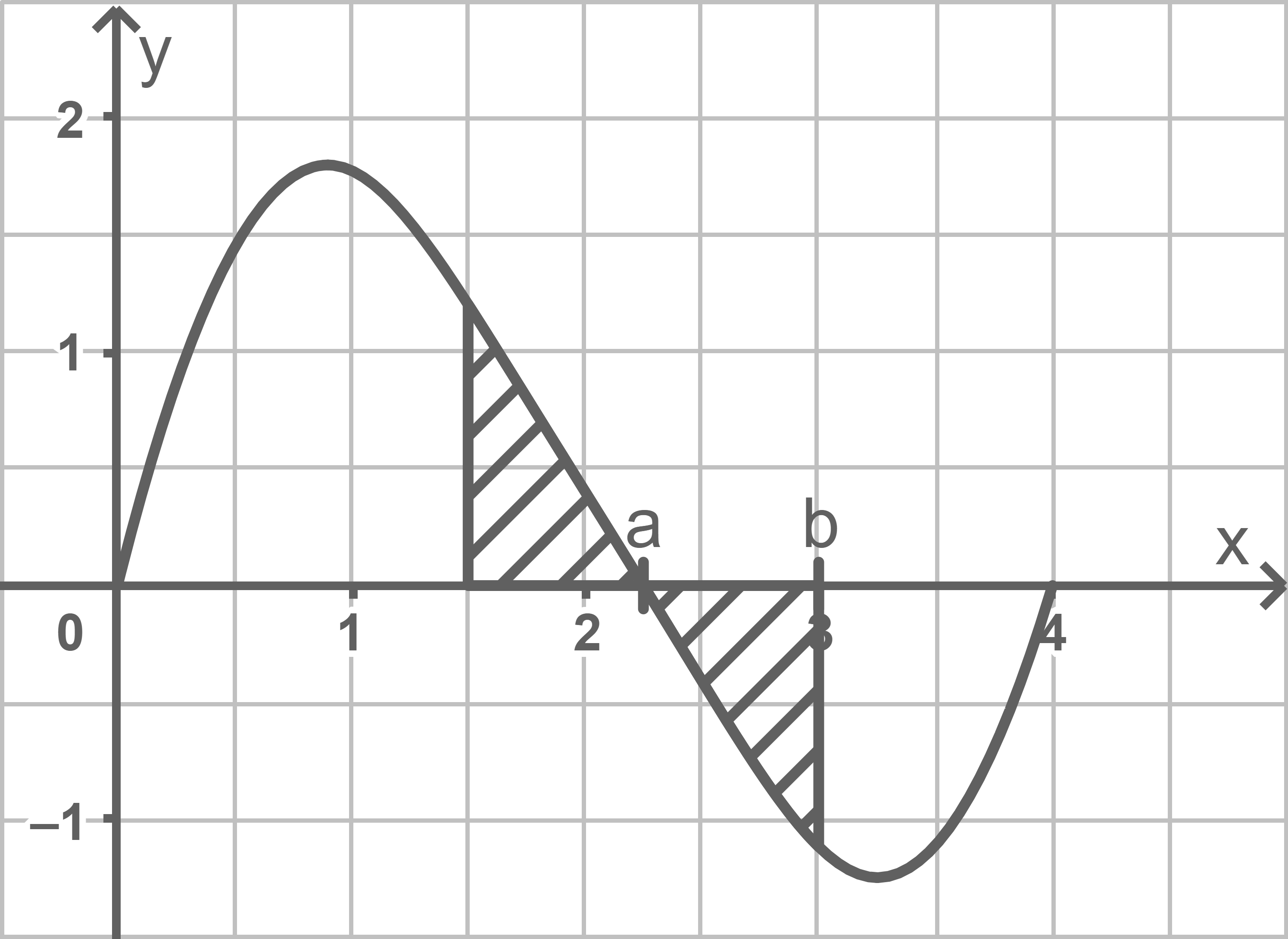
Der gesuchte Zeitpunkt wird mit  bezeichnet. Die Inhalte der Flächen, die der Graph mit der
bezeichnet. Die Inhalte der Flächen, die der Graph mit der  -Achse für
-Achse für  und
und  einschließt, müssen übereinstimmen.
einschließt, müssen übereinstimmen.
1.2
a)
Für alle Werte von  ist der Term von
ist der Term von  jeweils ein Polynom, wobei
jeweils ein Polynom, wobei  der Summand mit dem größten Exponenten ist.
Damit gilt
der Summand mit dem größten Exponenten ist.
Damit gilt  für ungerade Werte von
für ungerade Werte von  und
und  für gerade.
für gerade.
b)
Für  und
und  hat
hat  jeweils für alle Werte von
jeweils für alle Werte von  den gleichen Wert.
Es ergibt sich also für
den gleichen Wert.
Es ergibt sich also für  und
und 

 Somit haben alle Graphen der Schar die Punkte
Somit haben alle Graphen der Schar die Punkte  und
und  gemeinsam.
gemeinsam.
c)
d)
Trapezform begründen
Die Punkte  und
und  sowie die Punkte
sowie die Punkte  und
und  haben jeweils übereinstimmende
haben jeweils übereinstimmende  -Koordinaten.
Damit sind die Seiten
-Koordinaten.
Damit sind die Seiten  und
und  parallel.
Aussage nachweisen
Für gerade Werte von
parallel.
Aussage nachweisen
Für gerade Werte von  mit
mit  folgt also:
folgt also:
![\(\begin{array}[t]{rll}
A_k&=& \left| 1+1-k \right|+\left| 1+1+k \right| & \\[5pt]
&=&(k-2)+(2+k) & \\[5pt]
&=& 2k \left[\text{FE}\right]& \\[5pt]
\end{array}\)](https://mathjax.schullv.de/5512e07cdc2c1787ed60127145a121dd98eb87a644e03381a7b7db8e416d8f55?color=5a5a5a) Somit stimmen für jeden geraden Wert von
Somit stimmen für jeden geraden Wert von  mit
mit  der Flächeninhalt des Trapez für
der Flächeninhalt des Trapez für  und der Flächeninhalt des Trapez für
und der Flächeninhalt des Trapez für  überein.
überein.