Aufgabe 3.2: Stochastik
Ein Unternehmen produziert Stahlkugeln für Kugellager. Erfahrungsgemäß sind 4 % aller Kugeln fehlerhaft.
800 Kugeln werden zufällig ausgewählt. Die Anzahl der fehlerhaften Kugeln unter den ausgewählten kann durch eine binomialverteilte Zufallsgröße beschrieben werden.
800 Kugeln werden zufällig ausgewählt. Die Anzahl der fehlerhaften Kugeln unter den ausgewählten kann durch eine binomialverteilte Zufallsgröße beschrieben werden.
a)
Bestimme die Wahrscheinlichkeit dafür, dass unter den ausgewählten Kugeln weniger als 30 fehlerhaft sind.
(2 BE)
b)
Bestimme die Wahrscheinlichkeit dafür, dass die Anzahl der fehlerhaften Kugeln unter den ausgewählten höchstens um eine halbe Standardabweichung vom Erwartungswert dieser Anzahl abweicht.
Eine fehlerhafte Kugel hat entweder einen Formfehler oder einen Größenfehler. Die Wahrscheinlichkeit dafür, dass eine Kugel einen Formfehler hat, beträgt 3 %. Alle Kugeln werden vor dem Verpacken geprüft. Dabei werden 95 % der Kugeln mit Formfehler, 98 % der Kugeln mit Größenfehler, aber auch 0,5 % der Kugeln ohne Fehler aussortiert.
(5 BE)
c)
Stelle den Sachzusammenhang in einem beschrifteten Baumdiagramm dar.
(4 BE)
d)
Berechne die Wahrscheinlichkeit dafür, dass eine aussortierte Kugel keinen Formfehler hat.
Aufgrund zunehmender Reklamationen wird vermutet, dass der Anteil der fehlerhaften Kugeln auf über 4 % angestiegen ist. Bei einer Überprüfung in einer Stichprobe von 500 Kugeln werden 5 % fehlerhafte Kugeln festgestellt.
(3 BE)
e)
Zeige mithilfe eines Vertrauensintervalls für den unbekannten Anteil fehlerhafter Kugeln, dass die Vermutung dennoch nicht mit einer Vertrauenswahrscheinlichkeit von 95 % gestützt werden kann.
(4 BE)
f)
Ermittle den erforderlichen Umfang einer Stichprobe, in der dieselbe Fehlerquote von 5 % mit der Vertrauenswahrscheinlichkeit von 95 % dazu berechtigen würde, die Vermutung als erwiesen anzusehen.
(3 BE)
g)
Die Kugeln werden in Packungen verkauft. Ein Teil der verkauften Packungen wird zurückgegeben. Die Wahrscheinlichkeit dafür, dass eine verkaufte Packung zurückgegeben wird, beträgt 3 %. Dem Unternehmen entsteht pro Packung, die zurückgegeben wird, ein Verlust von 5,80 Euro; pro Packung, die nicht zurückgegeben wird, erzielt das Unternehmen einen Gewinn von 8,30 Euro. Bestimme die Wahrscheinlichkeit, mit der das Unternehmen bei einem Verkauf von 200 Packungen einen Gesamtgewinn von mindestens 1500 Euro erzielt.
(4 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Betrachtet wird die Zufallsgröße 
die die zufällige Anzahl der fehlerhaften Stahlkugeln beschreibt. 
kann laut Aufgabenstellung als binomialverteilt mit 
und 
angenommen werden: 
Mit einer passenden Tabelle zur kumulierten Binomialverteilung oder dem Taschenrechner ergibt sich:
Mit einer Wahrscheinlichkeit von ca. 33 % sind weniger als 30 der 800 Stahlkugeln fehlerhaft.
b)
Aufgrund der Binomialverteilung von ergibt sich für den Erwartungswert und die Standardabweichung:
Für die Wahrscheinlichkeit ergibt sich also:
Mit einer Wahrscheinlichkeit von ca. 35 % weicht die Anzahl der fehlerhaften Kugeln um höchstens eine halbe Standardabweichung vom Erwartungswert ab.
c)
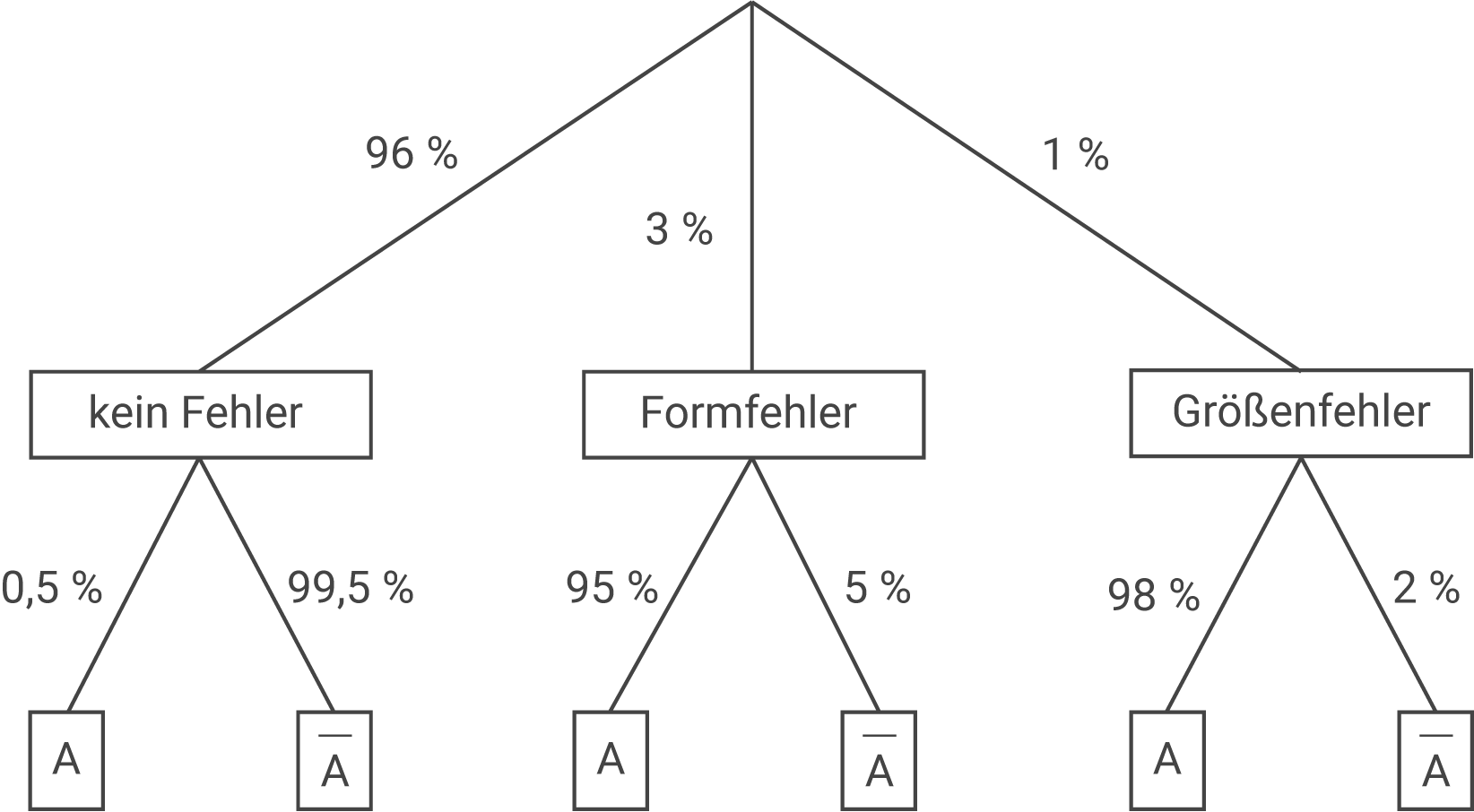
d)
Mit den Pfadregeln folgt:
Mit einer Wahrscheinlichkeit von ca. 34 % hat eine aussortierte Kugel keinen Formfehler.
e)
Die Sigma-Regeln können nur angewendet werden, wenn die Standardabweichung größer als 
ist:
Mit den Sigma-Regeln und der Formel für Vertrauensintervalle ergeben sich folgende Intervallgrenzen:
![\(0,04 \in [0,0309; 0,0691]\)](https://mathjax.schullv.de/8fccbd4bd31e0eaa6a8bd87381e2e4ca987e667846595eafbd55e7ab09495afe?color=5a5a5a)
Da die bisherige Wahrscheinlichkeit 
im Vertrauensintervall liegt, kann die Vermutung nicht mit einer Vertrauenswahrscheinlichkeit von 95 % gestützt werden.
f)
Damit nicht mehr im Vertrauensintervall liegt, müsste Folgendes gelten:
Die Stichprobe müsste aus mindestens 1825 Kugeln bestehen, um die Vermutung bei einer Vertrauenswahrscheinlichkeit von 95 % als erwiesen anzusehen.
g)
Die Zufallsgröße 
beschreibt die zufällige Anzahl 
der zurückgegebenen Packungen.
kann als binomialverteilt mit 
und 
angenommen werden: 
Damit das Unternehmen bei 
verkauften Packungen einen Gesamtgewinn von mindestens 
Euro erzielt, muss folgendes gelten:
Es dürfen also höchstens 
Packungen zurückgegeben werden. Die Wahrscheinlichkeit dafür beträgt:
Mit einer Wahrscheinlichkeit von ca. 
erwirtschaftet das Unternehmen mit Packungen einen Gewinn von mindestens Euro.