Pflichtaufgabe 1 - Analysis

1.1

Für jeden Wert von $k\in\mathbb{R}$ , $k\gt0,$ wird die in $\mathbb{R}$ definierte Funktion $h_k$ mit
$h_k(x)=10\cdot(1- \mathrm{e}^{-kx})\cdot \mathrm{e}^{-x}$ betrachtet.
Der Graph von $h_k$ wird mit $G_k$ bezeichnet.
Die Abbildung zeigt $G_1$ .

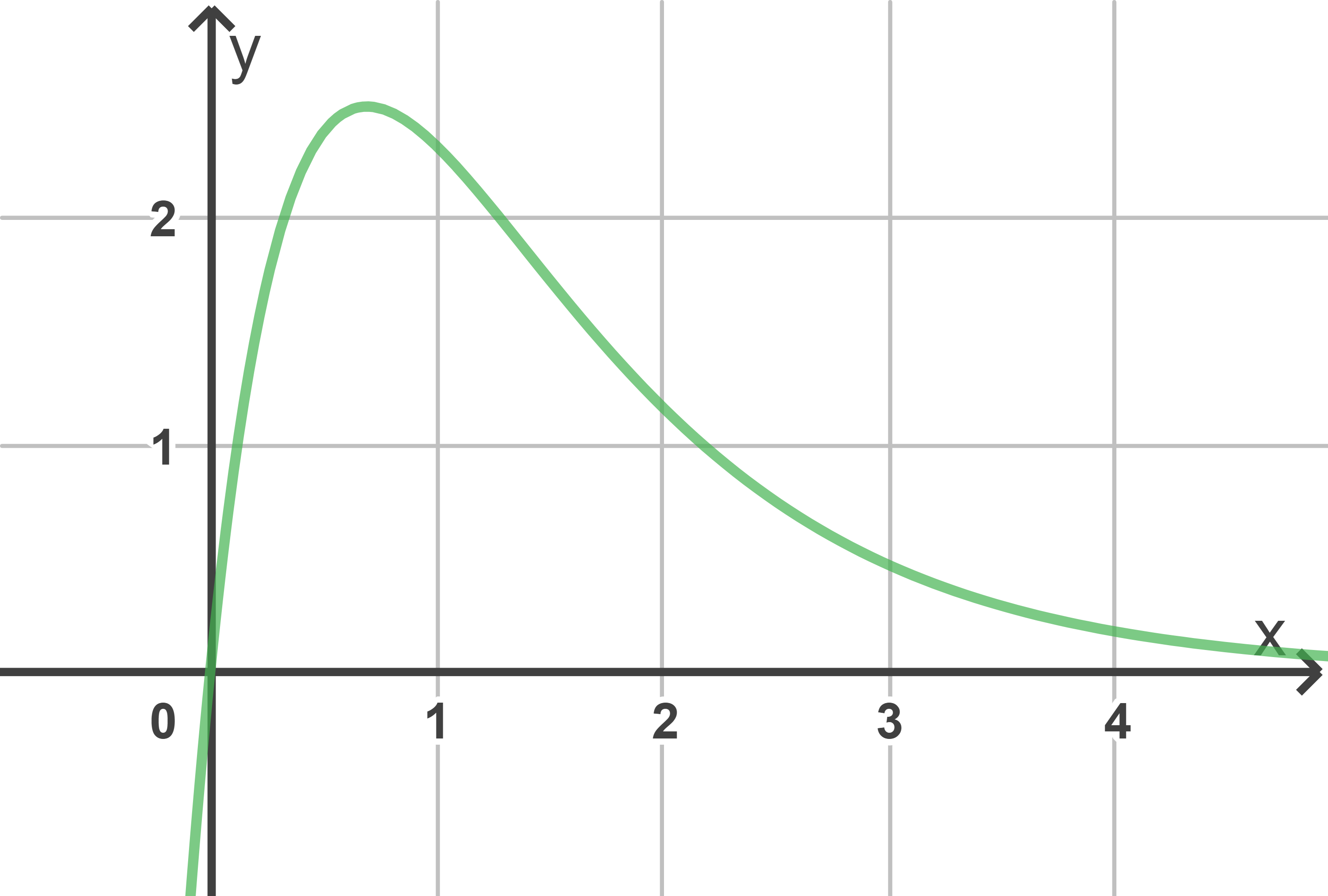
Graph einer mathematischen Funktion mit einer Kurve im Bereich von 0 bis 4 auf den Achsen x und y.

Begründe, dass $h_k$ nur die Nullstelle $x=0$ hat.
Gib den Grenzwert von $h_k$ für $x\rightarrow +\infty$ an.

(3 BE)

Ermittle die erste Ableitungsfunktion $\(h$ von $h_k.$

[zur Kontrolle: $\(h$ ]

(2 BE)

Bestimme die $x$ -Koordinate des Hochpunkts von $G_k.$

(3 BE)

Betrachet werden die Tangente an $G_k$ im Koordinatenursprung und die Gerade, die zu dieser Tangente im Koordinatensystem senkrecht steht.
Diese beiden Geraden schneiden die Gerade mit der Gleichung $y=1.$
Zeige rechnerisch, dass der Abstand der beiden Schnittpunkte $10k+\dfrac{1}{10k}$ ist.

(5 BE)

Betrachtet man den Abstand aus Teilaufgabe 1.1d für alle Werte von $k$ , so ist dieser für einen Wert von $k$ am kleinsten.
Bestimme diesen Wert und gib den zugehörigen Abstand an.

(3 BE)

Begründe ohne Rechnung, dass gilt $\displaystyle\int_{1}^{3}(h_1(x)-1)\;\mathrm dx\gt0.$

(2 BE)

1.1

Um mögliche Nullstellen zu berechnen, setzt du $h_k(x)=0$ und löst nach $x$ auf. Um nach $x$ auflösen zu können, kürzt du zuerst $\mathrm{e^{-x}}$ . Übrig bleibt folglich ein Produkt mit dem Faktor $\mathrm{e^{-kx}}$ .
Eine Funktion der Form $\mathrm{e^{-kx}}$ löst du mit dem Logarithmus nach $x$ auf.
Das Ergebnis ist ein einzelner Wert. Deshalb existiert nur eine Nullstelle.

Der Grenzwert für $x\rightarrow + \infty$ lautet $\lim\limits_{x\to +\infty} h_k =0$ .

$h_k(x)=10 \mathrm{e}^{-x} - 10\mathrm{e}^{kx} \cdot \mathrm{e}^{-x}$

Vollständige Lösung anzeigen

Leite diese Funktion nun mit der Produktregel ab:

$\( h_k$

Vollständige Lösung anzeigen

Um die x-Koordinate des Hochpunktes zu bestimmen, wende das notwendige Kriterium für Extremstellen an.

$0,68 \approx x$

Vollständige Lösung anzeigen

Der Hochpunkt von $G_k$ liegt an der Stelle $x= \dfrac{\ln(k+1)}{k}$ .

Die allgemeine Tangentengleichung lautet $y_t=m \cdot x +b$ und die allgemeine Normalengleichung lautet $y_n=- \dfrac{1}{m} \cdot x +b$ .

Die Normale steht senkrecht auf der Tangente.
$m$ entspricht der Steigung des Graphen $G_k$ im Ursprung.

$\(\begin{array}[t]{rll} m&=& h_k$

Da die Normale und die Tangente durch den Ursprung verlaufen, schneiden sie die y-Achse nur im Ursprung. Daher gilt $b=0$ .
Die Gleichungen lauten somit $y_n=-\dfrac{1}{10k} x$ und $y_t=10k \cdot x$ .

Setze nun $y=1$ ein und löse nach $x$ auf.

$\begin{array}[t]{rll} 1&=&10k \cdot x &\quad \scriptsize \; \\[5pt] x_1&=&\dfrac{1}{10k} \end{array}$

$\begin{array}[t]{rll} 1&=& -\dfrac{1}{10k} \cdot x&\quad \scriptsize \; \\[5pt] x_2&=&-10k \end{array}$

Du berechnest den Abstand zwischen der Tangente und der Normalen mit der Differenz der beiden x-Koordinaten.

Der Abstand beträgt somit $\dfrac{1}{10k} -(-10k) = \dfrac{1}{10k} +10k$ .

Der Abstand wird durch die Funktion $d(k)=10k+ \dfrac{1}{10k}$ beschrieben.

Um das Minimum zu berechnen, bestimme zuerst die beiden Ableitungen von $d(k)$ .

$\(d$

Wende das notwendige Kriterium für Extremstellen an und löse $\(d$ nach $x$ auf.

$\(\begin{array}[t]{rll} 0&=& d$

Mit der hinreichenden Bedingung handelt es sich wegen $\(d$ um ein Minimum.

Setze nun $k=0,1$ in die Funktionsgleichung von $d$ ein.
Das Minimum liegt bei $(0,1 \mid 2)$ . Der kleinste Abstand entsteht also für $k=0,1$ und beträgt $2$ LE.

Das Integral $\displaystyle\int_{1}^{3}(h_1(x)-1)\;\mathrm dx$ stellt den Flächeninhalt im Intervall $[1;3]$ zwischen $G_1$ und $y=1$ dar.

$G_1$ und $y=1$ schließen im Intervall $[1;3]$ eine Fläche ein, deren Flächeninhalt du mit der Abbildung von $G_1$ abschätzen kannst. Du kannst genau sagen, dass dieser Flächeninhalt $\gt 0$ ist.
Das liegt daran, dass der Graph von $h_1$ oberhalb der Geraden $y=1$ verläuft. Aus diesem Grund ist $h_1 > 1$ für alle $x$ im Intervall $[1;3]$ .
Und somit ist der Wert des Integrals $\displaystyle\int_{1}^{3}(h_1(x)-1)\;\mathrm dx\gt 0$ .