Pflichtaufgabe 2 - Analytische Geometrie
2.1
Gegeben sind der Punkt  und die Gerade
und die Gerade  ,
, 
 und
und  liegen in der Ebene
liegen in der Ebene 
Ermittle eine Gleichung von in Koordinatenform.
(zur Kontrolle:
in Koordinatenform.
(zur Kontrolle:  )
)
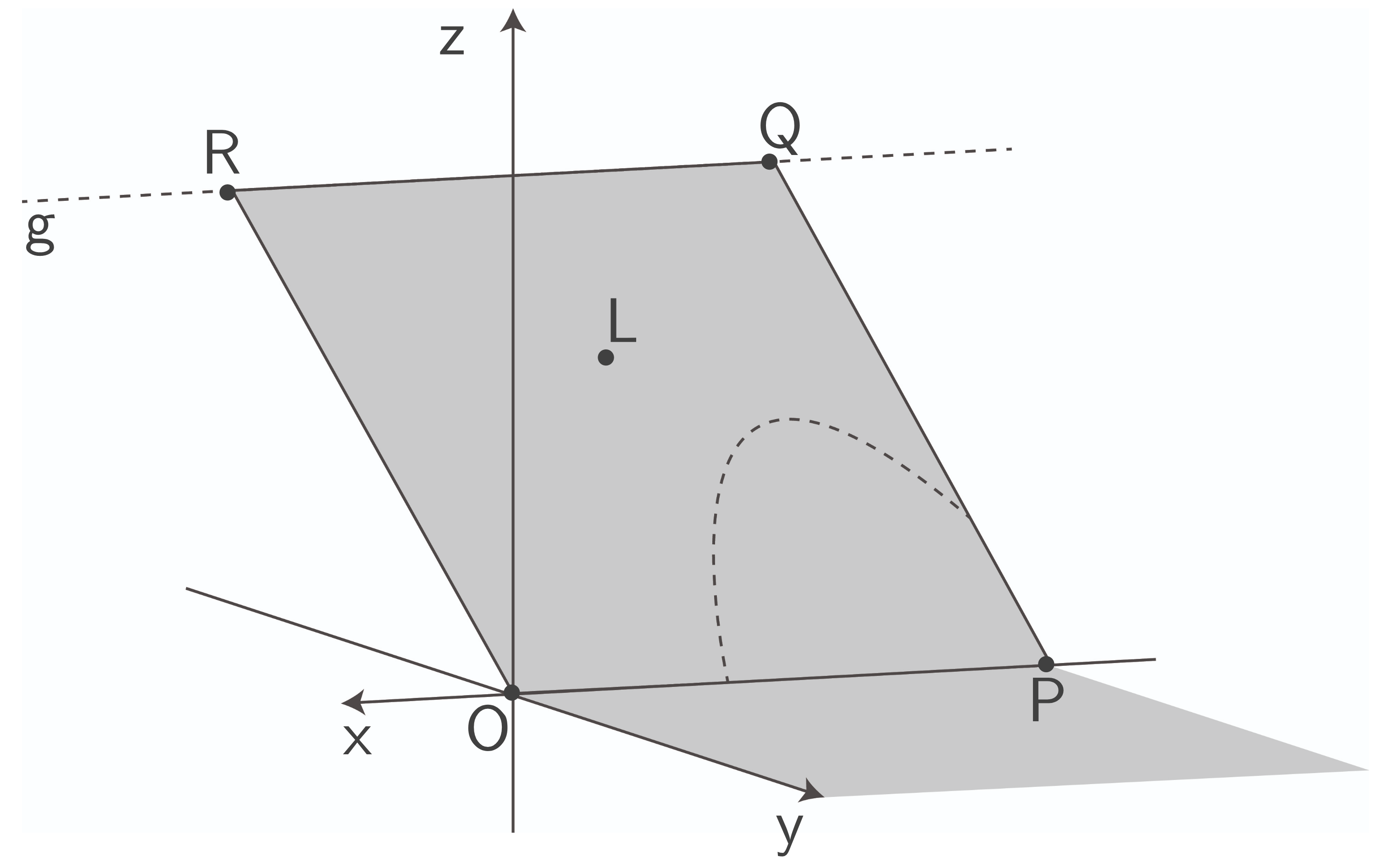
 stellt modellhaft den geneigten Teil einer Minigolfbahn dar, der Punkt
stellt modellhaft den geneigten Teil einer Minigolfbahn dar, der Punkt  das Loch dieser Bahn. Im verwendeten Koordinatensystem beschreibt die
das Loch dieser Bahn. Im verwendeten Koordinatensystem beschreibt die  -Ebene den horizontalen Untergrund; eine Längeneinheit entspricht
-Ebene den horizontalen Untergrund; eine Längeneinheit entspricht  in der Realität.
in der Realität.
 mit geeigneten Werten von
mit geeigneten Werten von  beschrieben werden.
beschrieben werden.
a)
Begründe, dass  parallel zur
parallel zur  -Achse und dabei nicht durch
-Achse und dabei nicht durch  verläuft.
verläuft.
(2 BE)
b)
Ermittle eine Gleichung von
(4 BE)
In der Abbildung ist neben  und
und  das Viereck
das Viereck  dargestellt, dessen Eckpunkte
dargestellt, dessen Eckpunkte  ,
,  ,
,  und
und  in
in  liegen.
liegen.  und
und  liegen außerdem auf
liegen außerdem auf  .
.

c)
Begründe, dass  ein Rechteck ist.
ein Rechteck ist.
(2 BE)
d)
Beschreibe ein Verfahren, mit dem man die Koordinaten des Punkts  ermitteln könnte, für den das Viereck
ermitteln könnte, für den das Viereck  ein ebenes Drachenviereck ist.
ein ebenes Drachenviereck ist.
Das Viereck
(3 BE)
e)
Berechne den Flächeninhalt des geneigten Teils der Bahn.
(2 BE)
f)
Berechne die Größe des Winkels, den der geneigte Teil der Bahn mit dem Untergrund einschließt.
Im Folgenden wird der in der Abbildung gestrichelt dargestellte Teil des Weges eines Minigolfballs betrachtet. Der Ball soll im Folgenden als punktförmig angenommen werden. Seine Positionen auf dem dargestellten Teil des Wegs können durch Punkte
g)
Weise nach, dass der Ball auf dem betrachteten Teil seines Wegs durchgehend Kontakt zur Minigolfbahn hat.
(2 BE)
h)
Berechne im Modell die Koordinaten des Punkts, in dem der Ball auf die seitliche Begrenzung der Minigolfbahn trifft.
(4 BE)
i)
Ermittle die maximale Höhe über dem Untergrund, die der Ball erreicht.
(3 BE)
2.1
a)
Ein Richtungsvektor der x-Achse ist  . Der Richtungsvektor der Geraden ist ebenfalls
. Der Richtungsvektor der Geraden ist ebenfalls  . Diese beiden Vektoren sind identisch, weshalb die Gerade parallel zur
. Diese beiden Vektoren sind identisch, weshalb die Gerade parallel zur  -Achse verläuft.
Die Geradendarstellung kannst du vereinfachen, nämlich zu
-Achse verläuft.
Die Geradendarstellung kannst du vereinfachen, nämlich zu  .
.
Alle Punkte auf der Geraden haben also die
haben also die  -Koordinate
-Koordinate  was auf
was auf  nicht zutrifft.
nicht zutrifft.
Die Gerade verläuft also nicht durch
verläuft also nicht durch 
Alle Punkte auf der Geraden
Die Gerade
b)
Um eine Ebenengleichung in Koordinatenform aufzustellen, brauchst du einen Normalenvektor, den du aus dem Kreuzprodukt zweier Spannvektoren berechnest.
Einen Spannvektor hast du bereits mit  .
Der Ortsvektor des Aufpunktes der Geraden
.
Der Ortsvektor des Aufpunktes der Geraden  ist
ist 
Zusammen mit dem Punkt ergibt sich ein zweiter Spannvektor zu:
ergibt sich ein zweiter Spannvektor zu:
 .
Für einen Normalenvektor folgt:
Du kannst die Ebenengleichung in Koordinatenform aufstellen mit
.
Für einen Normalenvektor folgt:
Du kannst die Ebenengleichung in Koordinatenform aufstellen mit  .
Setze die Koordinaten des Aufpunkts der Geraden ein, um
.
Setze die Koordinaten des Aufpunkts der Geraden ein, um  zu berechnen.
zu berechnen.
![\(\begin{array}[t]{rll}
c&=&3 \cdot (-12) +4\cdot 9 \\[5pt]
c&=&a -36+36 \\[5pt]
c&=&0
\end{array}\)](https://mathjax.schullv.de/0a6d6ceb60d4c739ee2ab273a8213db1cdb6f2b6c648fc995dfa664a7e72754b?color=5a5a5a) Mit
Mit  kommst du auf
kommst du auf 
Zusammen mit dem Punkt
c)
d)
Da  und
und  nicht gleich lang sind, verläuft die Symmetrieachse des Drachenvierecks zwischen
nicht gleich lang sind, verläuft die Symmetrieachse des Drachenvierecks zwischen  und
und 
Die zweite Diagonale verläuft von nach
nach  senkrecht zur Symmetrieachse und wird von dieser in der Mitte geteilt.
Um den fehlenden Punkt
senkrecht zur Symmetrieachse und wird von dieser in der Mitte geteilt.
Um den fehlenden Punkt  zu bestimmen, stelle also eine Gerade
zu bestimmen, stelle also eine Gerade  mit den Punkten
mit den Punkten  und
und  auf. Stelle dann eine Lotgerade vom Punkt
auf. Stelle dann eine Lotgerade vom Punkt  zu
zu  auf und bestimme den Schnittpunkt
auf und bestimme den Schnittpunkt  dieser beiden Geraden.
Den Punkt
dieser beiden Geraden.
Den Punkt  berechnest du dann mit
berechnest du dann mit  .
.
Die zweite Diagonale verläuft von
e)
Bestimme die Längen der Strecken mit dem Betrag der Vektoren.
Da 1 LE  in der Realität entspricht, berechnet sich der Flächeninhalt zu:
in der Realität entspricht, berechnet sich der Flächeninhalt zu:
f)
Ein Normalenvektor der xy-Ebene ist  . Ein Normalenvektor des geneigten Teils der Bahn lässt sich aus der Ebenengleichung ablesen und ist demnach
. Ein Normalenvektor des geneigten Teils der Bahn lässt sich aus der Ebenengleichung ablesen und ist demnach  .
Die Größe des Winkels zwischen zwei Ebenen lässt sich wie folgt berechnen:
.
Die Größe des Winkels zwischen zwei Ebenen lässt sich wie folgt berechnen:



g)
Liegt  in der Ebene
in der Ebene  so hat der Ball die ganze Zeit Kontakt zur Minigolfbahn.
so hat der Ball die ganze Zeit Kontakt zur Minigolfbahn.
Setze dazu in die Ebenengleichung ein:
in die Ebenengleichung ein:
![\(\begin{array}[t]{rll}
3 \cdot (-8k + \frac{8}{3}k^2) +4 \cdot (6k-2k^2)&=&0 &\quad \scriptsize \; \\[5pt]
-24k+8k^2+24k-8k^2&=&0 &\quad \scriptsize \; \\[5pt]
0&=&0
\end{array}\)](https://mathjax.schullv.de/9c412b20c43de93f476371de272704b6f2b1329e2b27c62491ed012f8380b513?color=5a5a5a) Folglich liegt
Folglich liegt  in der Ebene
in der Ebene  in der die Minigolfbahn liegt und der Ball hat Bodenkontakt.
in der die Minigolfbahn liegt und der Ball hat Bodenkontakt.
Setze dazu
h)
Zu berechnen sind die Koordinaten des Punktes, in dem  auf die Begrenzung
auf die Begrenzung  trifft.
trifft.  liegt auf der Geraden
liegt auf der Geraden  Setze
Setze  und
und  gleich.
gleich.
 Es ergeben sich die folgenden drei Gleichungen:
Es ergeben sich die folgenden drei Gleichungen:
 Aus der ersten Gleichung ergibt sich:
Aus der ersten Gleichung ergibt sich:
 Dies kannst du in die dritte Gleichung einsetzen und erhältst:
Dies kannst du in die dritte Gleichung einsetzen und erhältst:
 Setze nun
Setze nun  und
und  in die zweite Gleichung ein und überprüfe das Ergebnis.
in die zweite Gleichung ein und überprüfe das Ergebnis.
 Somit schneiden sich
Somit schneiden sich  und die Gerade
und die Gerade  für
für  und
und  .
.
Setze nun in
in  ein.
ein.

 Der Ball trifft im Punkt
Der Ball trifft im Punkt  auf den Rand der Bahn.
auf den Rand der Bahn.
Setze nun
i)
Die maximale Höhe entspricht dem Maximum der z-Koordinate.
Betrachte die z-Koordinate als Funktion in Abhängigkeit von
als Funktion in Abhängigkeit von  Du musst also
Du musst also  ableiten und das notwendige Kriterium für Extremstellen anwenden.
ableiten und das notwendige Kriterium für Extremstellen anwenden.


![\(\begin{array}[t]{rll}
z](https://mathjax.schullv.de/8d68901f69b16f2edecaebef1f827c47cbd833deb0d1599cdf373df5752df71a?color=5a5a5a) Setze nun
Setze nun  in
in  ein, um die Höhe zu berechnen:
ein, um die Höhe zu berechnen:
![\(\begin{array}[t]{rll}
z(1,5)&=& 6\cdot(1,5)-2\cdot(1,5)^2 \\[5pt]
z(1,5)&=&4,5
\end{array}\)](https://mathjax.schullv.de/08fddef6d12442e636981236868f6357a34400a6fa3997e22312a47aaa4ea45b?color=5a5a5a) Die maximale Höhe über dem Untergrund beträgt
Die maximale Höhe über dem Untergrund beträgt  .
.
Betrachte die z-Koordinate