Pflichtaufgabe 3 - Stochastik
3.1
Ein Unternehmen stellt in großer Stückzahl technische Geräte her. Ein Viertel der hergestellten Geräte ist fehlerhaft. Die Anzahl fehlerhafter Geräte in einer Stichprobe soll modellhaft als binomialverteilt angenommen werden.
a)
B: „Mehr als fünf Geräte sind fehlerhaft.“
C: „Mindestens drei, aber weniger als acht Geräte sind fehlerhaft.“
(5 BE)
b)
Beschreibe im Sachzusammenhang ein Zufallsexperiment, bei dem die Wahrscheinlichkeit eines Ereignisses mit dem Term  berechnet werden kann. Gib dieses Ereignis an.
berechnet werden kann. Gib dieses Ereignis an.
(3 BE)
c)
Von den fehlerhaften Geräten werden  so nachbearbeitet, dass sie ebenfalls fehlerfrei sind. Alle fehlerfreien Geräte werden ausgeliefert. Berechne die Wahrscheinlichkeit dafür, dass ein zufällig ausgewähltes ausgeliefertes Gerät nachbearbeitet wurde.
so nachbearbeitet, dass sie ebenfalls fehlerfrei sind. Alle fehlerfreien Geräte werden ausgeliefert. Berechne die Wahrscheinlichkeit dafür, dass ein zufällig ausgewähltes ausgeliefertes Gerät nachbearbeitet wurde.
(4 BE)
Kurz nach einer Änderung im Herstellungsverfahren stellt das Unternehmen den Anteil fehlerhafter Geräte von  infrage. Um bei einer Vertrauenswahrscheinlichkeit von
infrage. Um bei einer Vertrauenswahrscheinlichkeit von  einen Schätzwert für den Anteil fehlerhafter Geräte zu ermitteln, wird eine Stichprobe von
einen Schätzwert für den Anteil fehlerhafter Geräte zu ermitteln, wird eine Stichprobe von  Geräten betrachtet.
Geräten betrachtet.
Abbildung 1 zeigt die Graphen der folgenden für![\(p\in [0;1]\)](https://mathjax.schullv.de/8e374375d1d438c760a2c38184939f72fa220d9c623797fcc44369db2643ff31?color=5a5a5a) definierten Funktionen:
definierten Funktionen:


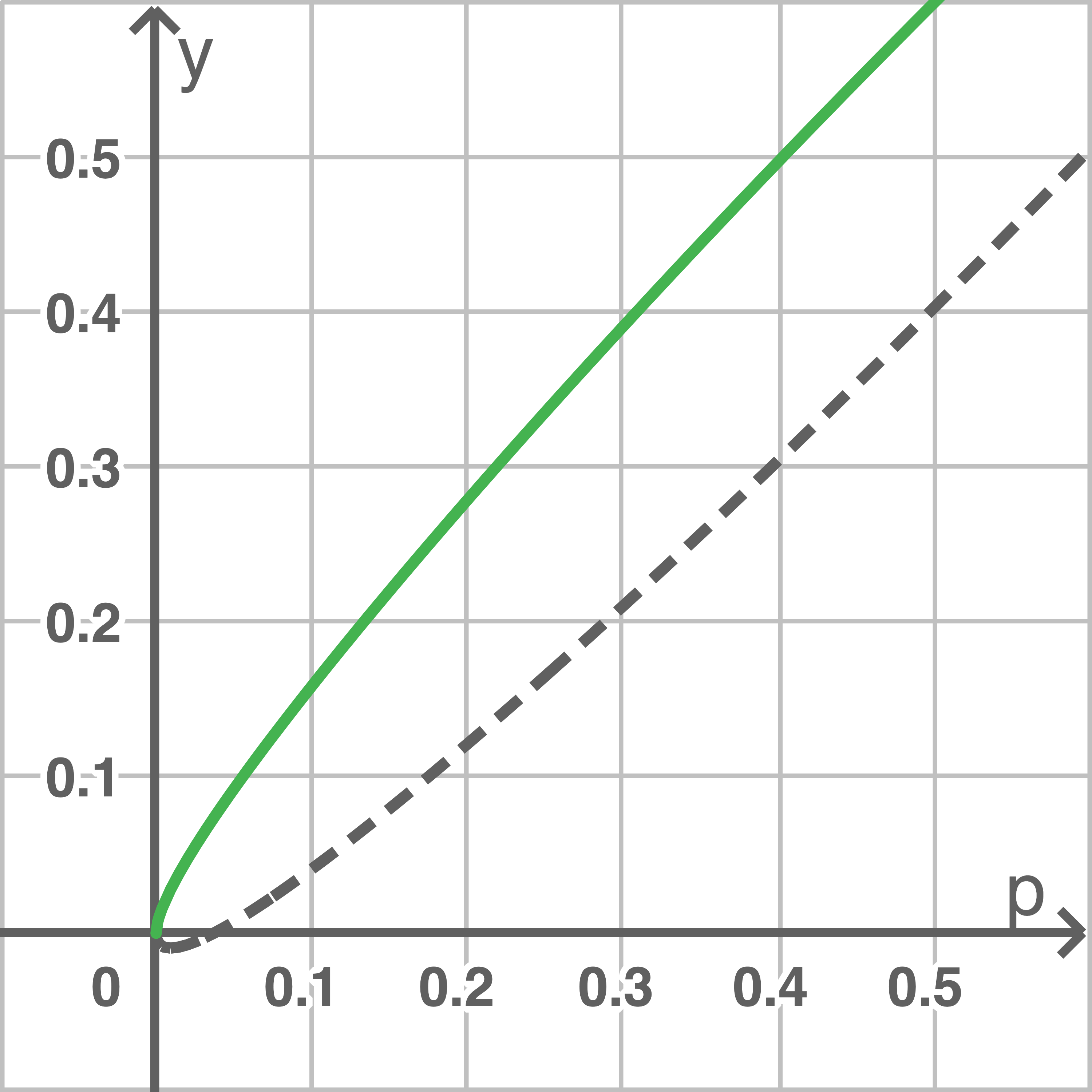
Abbildung 1 zeigt die Graphen der folgenden für

Abbildung 1
d)
Bestimme grafisch alle möglichen Anzahlen fehlerhafter Geräte in der Stichprobe, für die bei einer Sicherheitswahrscheinlichkeit von  jeweils Anlass dazu bestehen würde, die Korrektheit des gegebenen Anteils fehlerhafter Geräte infrage zu stellen.
jeweils Anlass dazu bestehen würde, die Korrektheit des gegebenen Anteils fehlerhafter Geräte infrage zu stellen.
(3 BE)
e)
Die betrachtete Stichprobe enthält  fehlerhafte Geräte. Bestimme grafisch das zu dieser Anzahl gehörende Vertrauensintervall zur Sicherheitswahrscheinlichkeit
fehlerhafte Geräte. Bestimme grafisch das zu dieser Anzahl gehörende Vertrauensintervall zur Sicherheitswahrscheinlichkeit 
(3 BE)
3.2
Eine binomialverteilte Zufallsgröße  gibt für eine Trefferwahrscheinlichkeit
gibt für eine Trefferwahrscheinlichkeit  mit
mit  die Anzahl der Treffer bei
die Anzahl der Treffer bei  Versuchen an.
Versuchen an.
a)
Abbildung 2 zeigt die symmetrische Wahrscheinlichkeitsverteilung einer Zufallsgröße mit der Wertemenge 
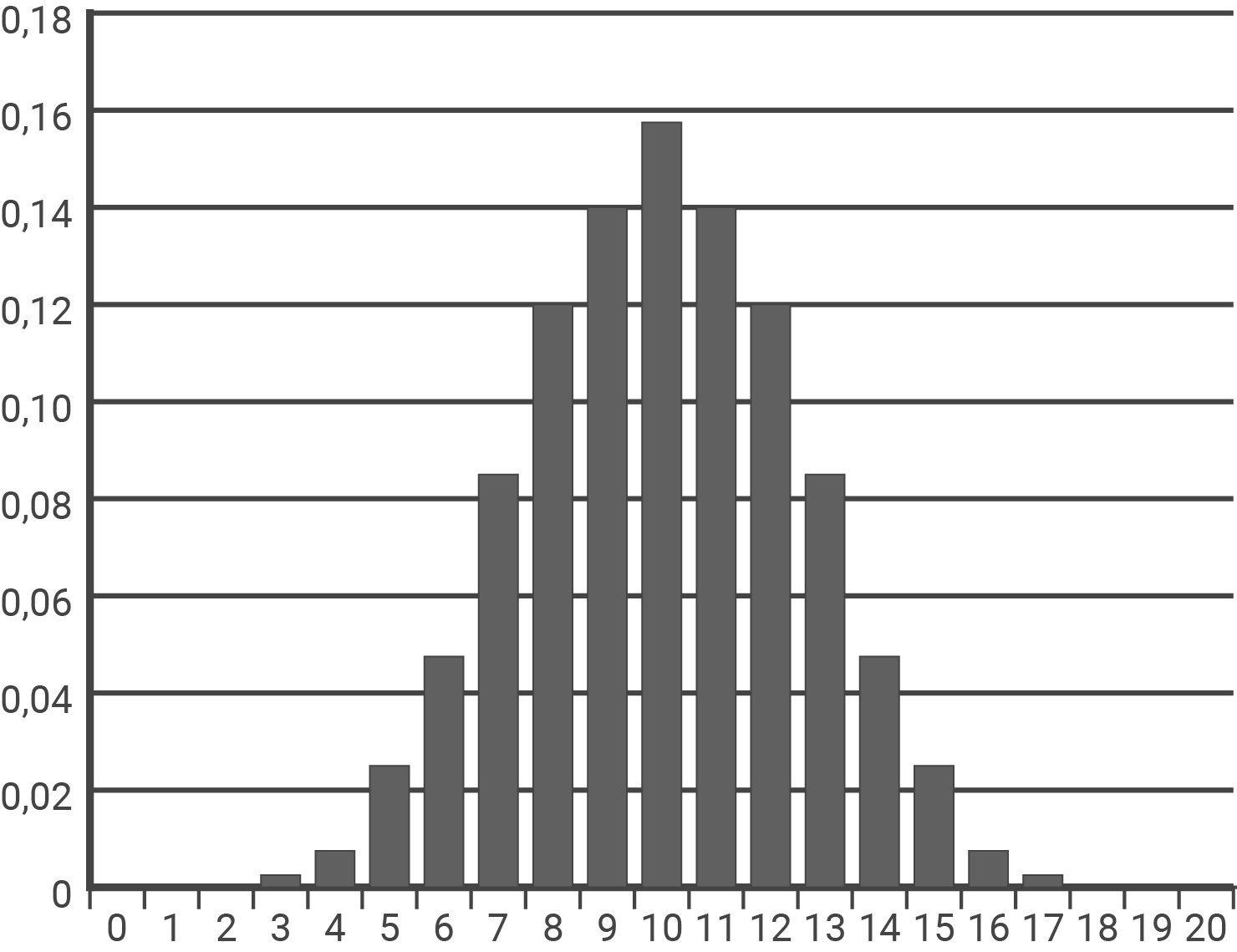 Begründe, dass es sich nicht um die Wahrscheinlichkeitsverteilung von
Begründe, dass es sich nicht um die Wahrscheinlichkeitsverteilung von  handeln kann.
handeln kann.

Abbildung 2
(3 BE)
b)
Bestimme diejenigen Werte von  die für die Wahrscheinlichkeit dafür, dass
die für die Wahrscheinlichkeit dafür, dass  den Wert
den Wert  annimmt,
annimmt,  ist.
ist.
(4 BE)
3.1
a)
Betrachtet wird die Zufallsgröße  die die zufällige Anzahl der fehlerhaften Geräte unter
die die zufällige Anzahl der fehlerhaften Geräte unter  zufällig ausgewählten Geräten beschreibt. Diese wird laut Aufgabenstellung als binomialverteilt angenommen mit
zufällig ausgewählten Geräten beschreibt. Diese wird laut Aufgabenstellung als binomialverteilt angenommen mit  und
und  angenommen.
angenommen.
b)
c)
Der Anteil der ausgelieferten Gerät unter allen hergestellten Geräten ergibt sich mit den Pfadregeln zu:
 Der Anteil der Geräte, die durch eine Nachbearbeitung fehlerfrei ausgeliefert werden können beträgt:
Der Anteil der Geräte, die durch eine Nachbearbeitung fehlerfrei ausgeliefert werden können beträgt:
 Insgesamt folgt dann:
Insgesamt folgt dann:
 Mit einer Wahrscheinlichkeit von ca.
Mit einer Wahrscheinlichkeit von ca.  ist ein zufällig ausgewähltes ausgeliefertes Gerät nachbearbeitet worden.
ist ein zufällig ausgewähltes ausgeliefertes Gerät nachbearbeitet worden.
d)
Für  lässt sich aus der Abbildung ablesen:
lässt sich aus der Abbildung ablesen:
 und
und  Liegt also der Anteil fehlerhafter Geräte in der Stichprobe unter
Liegt also der Anteil fehlerhafter Geräte in der Stichprobe unter  oder über
oder über  so bestünde unter einer Sicherheitswahrscheinlichkeit von
so bestünde unter einer Sicherheitswahrscheinlichkeit von  Anlass dazu den Anteil fehlerhafter Geräte infrage zu stellen.
Anlass dazu den Anteil fehlerhafter Geräte infrage zu stellen.
Für die Anzahl der fehlerhaften Geräte in der Stichprobe von Geräten bedeutet das:
Geräten bedeutet das:
 und
und  Befinden sich unter den
Befinden sich unter den  überprüften Geräten weniger als
überprüften Geräten weniger als  oder mehr als
oder mehr als  so bestünde unter einer Sicherheitswahrscheinlichkeit von
so bestünde unter einer Sicherheitswahrscheinlichkeit von  Anlass dazu den Anteil fehlerhafter Geräte infrage zu stellen.
Anlass dazu den Anteil fehlerhafter Geräte infrage zu stellen.
Für die Anzahl der fehlerhaften Geräte in der Stichprobe von
e)
Für  ergibt sich aus der Abbildung:
ergibt sich aus der Abbildung:
 und
und  Zu der Stichprobe mit
Zu der Stichprobe mit  fehlerhaften von insgesamt
fehlerhaften von insgesamt  Geräten gehört mit einer Vertrauenswahrscheinlichkeit von
Geräten gehört mit einer Vertrauenswahrscheinlichkeit von  das Vertrauensintervall
das Vertrauensintervall ![\([0,11;0,27].\)](https://mathjax.schullv.de/ba6d6234d67e5fc4556a6f5931436875c8f3cbf0e7e767164563a15eb9b2afcd?color=5a5a5a)
3.2
a)
In der Abbildung ist der Wert mit der größten Wahrscheinlichkeit  Dies müsste also der Erwartungswert der binomialverteilten Zufallsgröße sein. Mit der entsprechenden Formel für den Erwartungswert
Dies müsste also der Erwartungswert der binomialverteilten Zufallsgröße sein. Mit der entsprechenden Formel für den Erwartungswert  einer binomialverteilte Zufallsgröße und mit
einer binomialverteilte Zufallsgröße und mit  folgt:
Für eine binomialverteilte Zufallsgröße mit
folgt:
Für eine binomialverteilte Zufallsgröße mit  und
und  gilt wiederum:
In der Abbildung ist allerdings
gilt wiederum:
In der Abbildung ist allerdings 
Die dargestellte Wahrscheinlichkeitsverteilung kann also nicht zu einer binomialverteilten Zufallsgröße gehören, also insbesondere nicht zu der von
Die dargestellte Wahrscheinlichkeitsverteilung kann also nicht zu einer binomialverteilten Zufallsgröße gehören, also insbesondere nicht zu der von
b)
Für  und
und  beträgt die Wahrscheinlichkeit dafür, dass
beträgt die Wahrscheinlichkeit dafür, dass  den Wert
den Wert  annimmt, ca.
annimmt, ca. 