Aufgabe 3: Stochastik
Ein Unternehmen stellt Olivenöl her und füllt es in Flaschen ab. Laut Aufdruck beträgt die Füllmenge jeder Flasche 
3.1
Die Flaschen werden in Kartons verpackt; jeder Karton enthält zwölf Flaschen. Ein Karton gilt als fehlerhaft, wenn mehr als eine Flasche weniger als  Öl enthält. Für jede Flasche beträgt die Wahrscheinlichkeit dafür, dass sie weniger als
Öl enthält. Für jede Flasche beträgt die Wahrscheinlichkeit dafür, dass sie weniger als  Öl enthält,
Öl enthält, 
a)
Die Rechnung  stellt im Sachzusammenhang die Lösung einer Aufgabe dar.
Formuliere eine passende Aufgabenstellung und erläutere den Ansatz der Rechnung.
stellt im Sachzusammenhang die Lösung einer Aufgabe dar.
Formuliere eine passende Aufgabenstellung und erläutere den Ansatz der Rechnung.
(3 BE)
b)
An einen Supermarkt wird regelmäßig die gleiche Anzahl von Flaschen geliefert. Dabei enthalten im Mittel mehr als 780 Flaschen mindestens  Öl.
Ermittle, wie viele Flaschen mindestens geliefert werden.
Öl.
Ermittle, wie viele Flaschen mindestens geliefert werden.
(3 BE)
c)
Ein Supermarkt erhält eine Lieferung von 150 Kartons.
Bestimme die Wahrscheinlichkeit dafür, dass mehr als  der Kartons fehlerhaft sind.
der Kartons fehlerhaft sind.
(4 BE)
Das Unternehmen gibt den Anteil fehlerhaft etikettierter Kartons mit  an. Ein Abnehmer bezweifelt diese Angabe.
Zur Überprüfung der Angabe registriert der Abnehmer in einer Stichprobe vom Umfang
an. Ein Abnehmer bezweifelt diese Angabe.
Zur Überprüfung der Angabe registriert der Abnehmer in einer Stichprobe vom Umfang  einen Anteil
einen Anteil  fehlerhaft etikettierter Kartons.
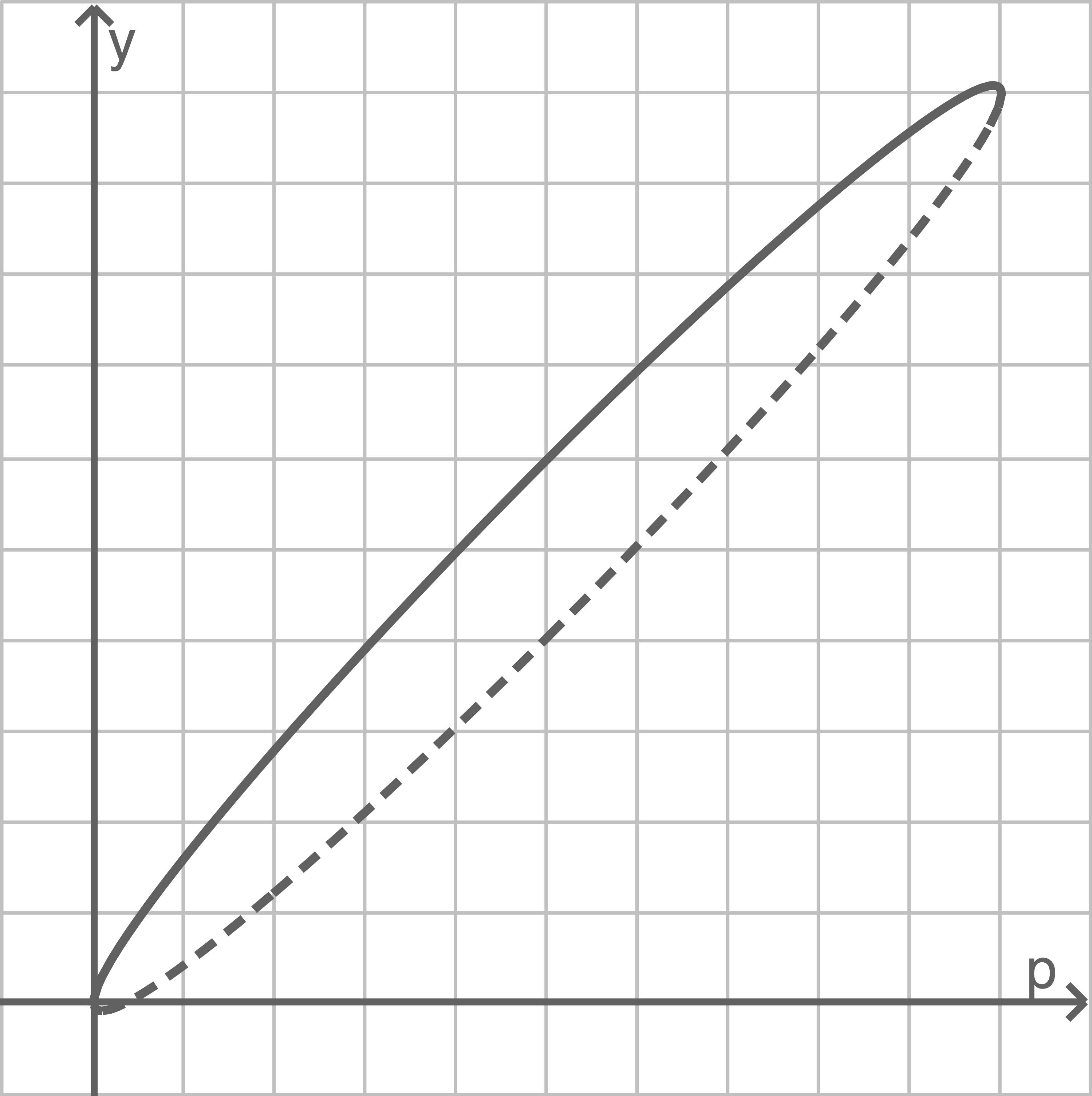
Die Abbildung zeigt für diese Stichprobe die Graphen der für
fehlerhaft etikettierter Kartons.
Die Abbildung zeigt für diese Stichprobe die Graphen der für ![\(p \in[0 ; 1]\)](https://mathjax.schullv.de/fb3e63f29a0c4152de7285dc6c77a2bec9288b289c10be67a40fbffeda9f8705?color=5a5a5a) definierten Funktionen:
definierten Funktionen:



d)
Veranschauliche die folgende wahre Aussage in der Abbildung und erläutere deine Veranschaulichung.
Die Überprüfung der Verträglichkeit des Stichprobenergebnisses  mit der Wahrscheinlichkeit
mit der Wahrscheinlichkeit  führt sowohl ausgehend von
führt sowohl ausgehend von  als auch von
als auch von  zum gleichen Resultat.
zum gleichen Resultat.
(3 BE)
3.2
Die Füllmenge der Flaschen soll als normalverteilt mit einem Erwartungswert von  und einer Standardabweichung von
und einer Standardabweichung von  angenommen werden.
angenommen werden.
a)
Eine Flasche wird zufällig ausgewählt. Ermittle für die folgenden Ereignisse jeweils die Wahrscheinlichkeit:
 "Die Flasche enthält mehr als
"Die Flasche enthält mehr als  Öl."
Öl."
 "Die Füllmenge der Flasche weicht höchstens um
"Die Füllmenge der Flasche weicht höchstens um  vom Erwartungswert ab."
vom Erwartungswert ab."
(3 BE)
b)
Die Füllmenge einer Flasche ist nie negativ. Die Normalverteilung, die zur Beschreibung der Füllmenge der Flaschen verwendet wird, ist jedoch auch für negative reelle Zahlen definiert und nimmt dabei ausschließlich positive Werte an.
Begründe, dass die Verwendung der Normalverteilung dennoch sinnvoll ist.
(2 BE)
3.3
Im Folgenden werden Ereignisse  und
und  eines Zufallsversuchs betrachtet.
In der Vierfeldertafel sind zugehörige Wahrscheinlichkeiten angegeben.
eines Zufallsversuchs betrachtet.
In der Vierfeldertafel sind zugehörige Wahrscheinlichkeiten angegeben.
a)
Bei einem Nachweis wurden folgende Argumentationsschritte in der angegebenen Reihenfolge durchgeführt:


 Erläutere für jeden Argumentationsschritt den zugrundeliegenden Gedankengang und zeige, dass damit
Erläutere für jeden Argumentationsschritt den zugrundeliegenden Gedankengang und zeige, dass damit  nachgewiesen wird.
nachgewiesen wird.
(4 BE)
b)
Die Wahrscheinlichkeit, dass von den Ereignissen  und
und  genau eines eintritt, beträgt
genau eines eintritt, beträgt  Vervollständige die Vierfeldertafel.
Vervollständige die Vierfeldertafel.
(3 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
3.1
a)
Aufgabenstellung formulieren
„Es wird ein Karton zufällig ausgewählt. Berechne die Wahrscheinlichkeit dafür, dass jede Flasche aus dem Karton mindestens  Öl enthält."
Ansatz erläutern
Wahrscheinlichkeit dafür, dass eine Flasche mindestens
Öl enthält."
Ansatz erläutern
Wahrscheinlichkeit dafür, dass eine Flasche mindestens  enthält:
enthält:
 Wahrscheinlichkeit dafür, dass alle 12 Flaschen aus einem Karton mindestens
Wahrscheinlichkeit dafür, dass alle 12 Flaschen aus einem Karton mindestens  enthalten:
enthalten:

b)
Das Mittel von mehr als 780 Flaschen entspricht dem Erwartungswert. Hierbei beschreibt  die Anzahl der gelieferten Flaschen.
Es soll gelten:
die Anzahl der gelieferten Flaschen.
Es soll gelten:
![\(\begin{array}[t]{rll}
\mu&\gt& 780& \\[5pt]
n\cdot 0,985&\gt& 780&\quad \scriptsize \mid\; :0,985 \\[5pt]
n&\gt& 791,9& \\[5pt]
\end{array}\)](https://mathjax.schullv.de/2248e52758dd584db77eb251373b7654b6c9a1d6cb90f324fb6fe462053a8c36?color=5a5a5a) Da die Anzahl der Flaschen eine natürliche Zahl sein muss, gilt
Da die Anzahl der Flaschen eine natürliche Zahl sein muss, gilt  Es werden also mindestens 792 Flaschen geliefert.
Es werden also mindestens 792 Flaschen geliefert.
c)
d)
In der Abbildung sind  und
und  für die Vertrauenswahrscheinlichkeit
für die Vertrauenswahrscheinlichkeit  dargestellt. Die
dargestellt. Die  -Achse stellt den Anteil
-Achse stellt den Anteil  fehlerhaft etikettierter Kartons dar.
Die Verträglichkeit des Stichprobenergebnisses
fehlerhaft etikettierter Kartons dar.
Die Verträglichkeit des Stichprobenergebnisses  mit der Wahrscheinlichkeit
mit der Wahrscheinlichkeit  kann mit zwei Vorgehensweisen überprüft werden:
kann mit zwei Vorgehensweisen überprüft werden:
 außerhalb des berechneten Prognoseintervalls bzw. liegt
außerhalb des berechneten Prognoseintervalls bzw. liegt  außerhalb des berechneten Vertrauensintervalls, bestünde unter einer Sicherheitswahrscheinlichkeit von
außerhalb des berechneten Vertrauensintervalls, bestünde unter einer Sicherheitswahrscheinlichkeit von  Anlass dazu den vom Unternehmen angegebenen Anteil fehlerhaft etikettierter Kartons infrage zu stellen.
Mit beiden Vorgehensweisen folgt das gleiche Ergebnis und deswegen auch die wahre Aussage für die Verträglichkeit des Stichprobenergebnisses
Anlass dazu den vom Unternehmen angegebenen Anteil fehlerhaft etikettierter Kartons infrage zu stellen.
Mit beiden Vorgehensweisen folgt das gleiche Ergebnis und deswegen auch die wahre Aussage für die Verträglichkeit des Stichprobenergebnisses  mit der Wahrscheinlichkeit
mit der Wahrscheinlichkeit  Das gleiche Resultat kommt daher zustande, dass die Graphen der Funktionen
Das gleiche Resultat kommt daher zustande, dass die Graphen der Funktionen  und
und  für die Intervallränder symmetrisch zueinander bezüglich der Winkelhalbierenden im ersten Quadranten sind.
Die Umkehrfunktion von
für die Intervallränder symmetrisch zueinander bezüglich der Winkelhalbierenden im ersten Quadranten sind.
Die Umkehrfunktion von  ist
ist  und es ist ebenso
und es ist ebenso  Mit gegebenem
Mit gegebenem  kann über die Umkehrfunktionenen von
kann über die Umkehrfunktionenen von  und
und  das Vertrauensintervall rechnerisch ermittelt werden. Wegen der Symmetrie von
das Vertrauensintervall rechnerisch ermittelt werden. Wegen der Symmetrie von  und
und  ergeben sich damit die gleichen Werte wie wenn anhand von
ergeben sich damit die gleichen Werte wie wenn anhand von  das Prognoseintervall bestimmt werden würde.
das Prognoseintervall bestimmt werden würde.
Prognoseintervall bestimmen
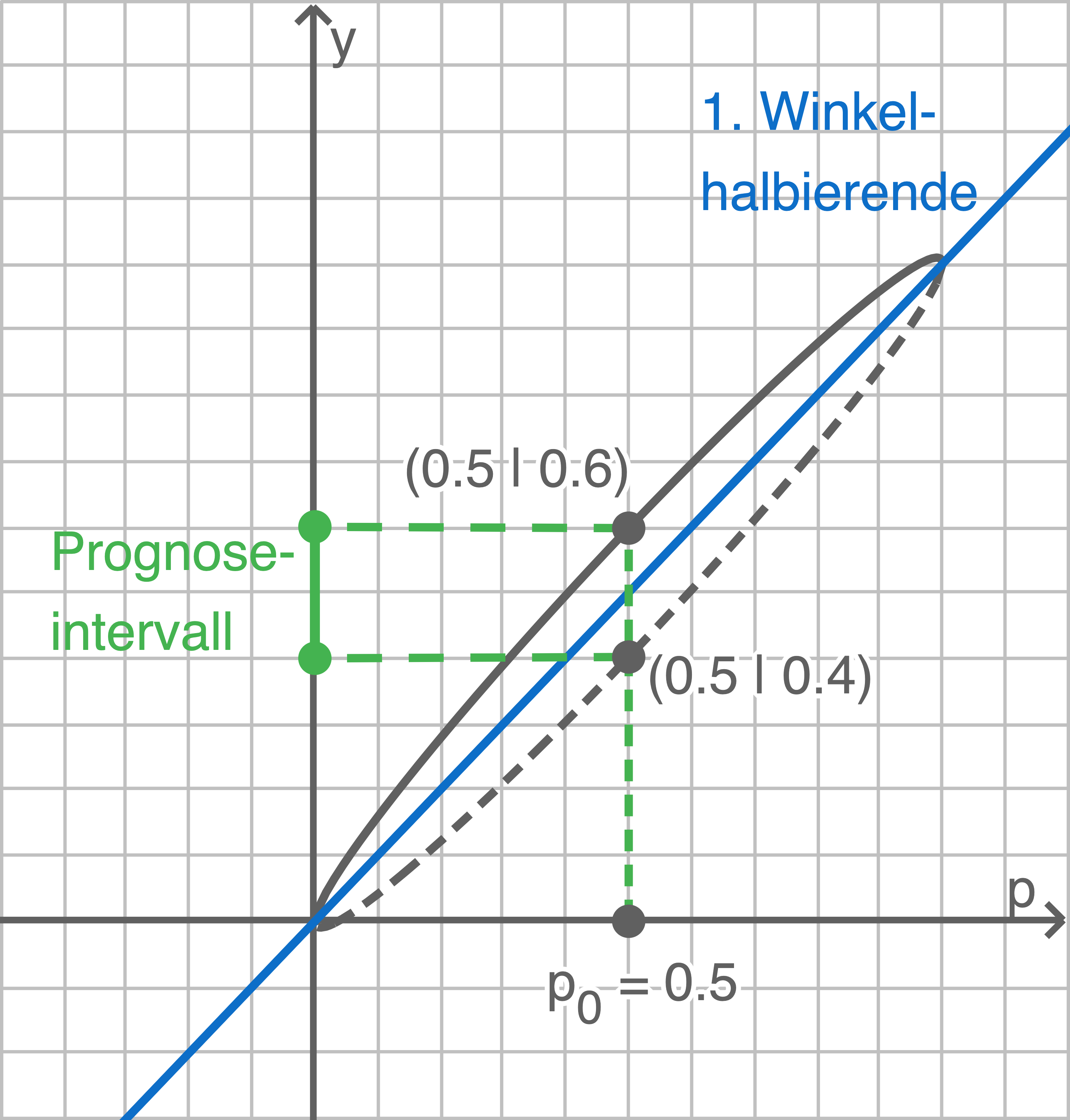 Beispielwerte: Für
Beispielwerte: Für  wird das Prognoseintervall
wird das Prognoseintervall ![\([0,4;0,6]\)](https://mathjax.schullv.de/fa9e5ab1978ee97ae513c08db7bdfa917ed1d502065bbfff6f18502ab01b716f?color=5a5a5a) abgelesen.
abgelesen.

Mögliche Veranschaulichung Prognoseintervall
Vertrauensintervall bestimmen
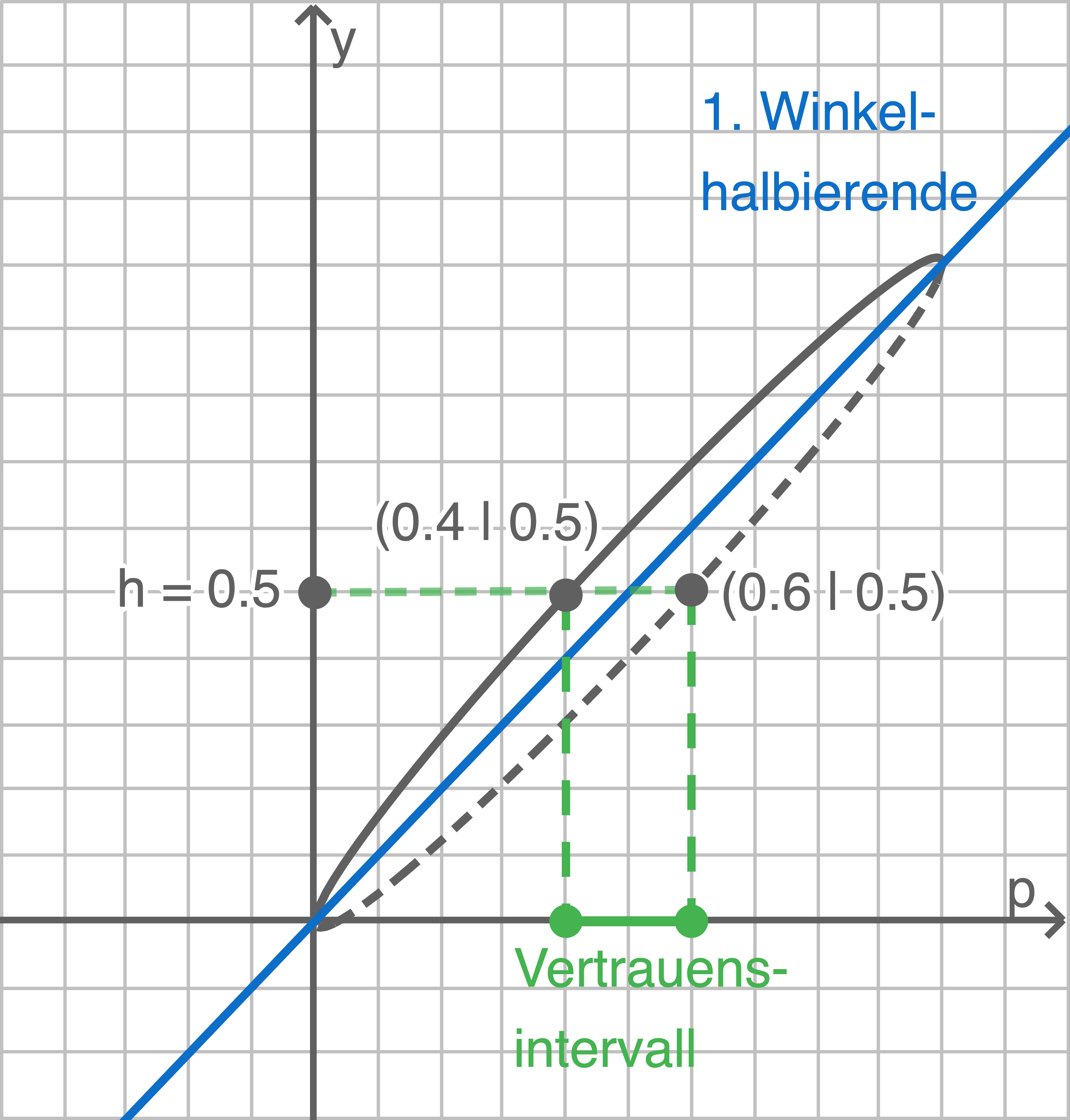 Beispielwerte: Für
Beispielwerte: Für  wird das Vertrauensintervall
wird das Vertrauensintervall ![\([0,4;0,6]\)](https://mathjax.schullv.de/fa9e5ab1978ee97ae513c08db7bdfa917ed1d502065bbfff6f18502ab01b716f?color=5a5a5a) abgelesen.
abgelesen.
Gesamtresultat
Liegt 
Mögliche Veranschaulichung Vertrauensintervall
3.2
a)
b)
Die verwendete Normalverteilung liefert für die negativen Füllmengen so geringe Wahrscheinlichkeiten, dass diese vernachlässigt werden können.
3.3
a)
b)
Für das beschriebene Ereignis  gilt:
Eintragen in die Vierfeldertafel ergibt:
gilt:
Eintragen in die Vierfeldertafel ergibt:
Nun folgt:
![\(\begin{array}[t]{rll}
P(\overline{D})&=& P(C\cap \overline{D})+P(\overline{C} \cap \overline{D})&\\[5pt]
&=& 0,3+0,45&\\[5pt]
&=& 0,75
\end{array}\)](https://mathjax.schullv.de/6e2cdbea75391c877f725592c5bed424b6683e64bfdc94d31008da6ccd567877?color=5a5a5a)
![\(\begin{array}[t]{rll}
P(D)&=& 1-P(\overline{D})& \\[5pt]
&=& 1-0,75& \\[5pt]
&=& 0,25
\end{array}\)](https://mathjax.schullv.de/2ff14fd02aa91f7bd43ce124bb74489fbf10cf74aa463bf4c369a4a23f618e6d?color=5a5a5a)
![\(\begin{array}[t]{rll}
P(C)&=& 1- P(\overline{C}) &\\[5pt]
&=& 1-0,70&\\[5pt]
&=& 0,30
\end{array}\)](https://mathjax.schullv.de/bcd928b8a832698b0a912408127ad008de19e8f2694e71922650562e8451d962?color=5a5a5a)
![\(\begin{array}[t]{rll}
P(C \cap D)&=& P(C)-P(C \cap \overline{D})&\\[5pt]
&=& 0,30-0,30&\\[5pt]
&=& 0
\end{array}\)](https://mathjax.schullv.de/2bfbfb5a22c2eb9bdc328aeff2fd1c91c311674dd66846a3062f691e6dd86cd7?color=5a5a5a) Somit ergibt sich die vollständige Vierfeldertafel mit:
Somit ergibt sich die vollständige Vierfeldertafel mit: