Teil B1 - Analysis

Für jede von Null verschiedene reelle Zahl $k$ ist eine Funktion $f_k$ gegeben.

$f_k(x)=(k \cdot x-1) \cdot \mathrm e^{k \cdot x+1} \;(x \in \mathbb{R})$

Begründe anhand des Funktionsterms, dass jeder Graph von $f_k$ als einzigen Schnittpunkt mit der $x$ -Achse den Punkt $S_k\left(\left.\frac{1}{k} \right\rvert\, 0\right)$ hat.

(2 BE)

Untersuche die Graphen der Funktionen $f_k$ auf lokale Extrempunkte und Wendepunkte.
Beschreibe den Einfluss von $k$ auf die Lage dieser Punkte.

(8 BE)

Die Graphen der Funktionen $f_k$ und $f_{-k}$ begrenzen mit der $x$ -Achse eine Fläche vollständig.
Bestimme einen Wert für $k,$ so dass diese Fläche einen Inhalt von $2\;\mathrm{FE}$ besitzt.

(3 BE)

Für jede positive reelle Zahl $k$ bilden der Koordinatenursprung $O,$ der Schnittpunkt $S_{k}$ des Graphen von $f_k$ mit der $x$ -Achse und die Punkte $P(0 \mid-\mathrm e)$ sowie $R_{k}\left(\left.-\frac{1}{k} \right\rvert\,-2\right)$ ein Viereck.
Zeige, dass die $y$ -Achse die Vierecke je in zwei flächengleiche Dreiecke teilt.
Für eines der Vierecke hat der Winkel $\sphericalangle\; OS_kP$ eine Größe von $45^{\circ}.$
Berechne den Flächeninhalt dieses Vierecks.

(6 BE)

Der Graph einer quadratischen und zur $y$ -Achse symmetrischen Funktion $q_k$ verläuft durch die Punkte $S_k$ und $P(0 \mid-\mathrm e).$
Berechne für positive Werte von $k$ die Stelle $x$ mit $0\lt x\lt\frac{1}{k},$ an der die Differenz der Funktionswerte von $q_k$ und $f_k$ am größten ist.
Zeige, dass diese Differenz einen konstanten Wert besitzt.

(8 BE)

Die Höhe einer Pflanzenart wurde über einen bestimmten Beobachtungszeitraum dokumentiert und kann aufgrund der Messergebnisse mit der Funktion $h$ beschrieben werden.

$h(t)=\left(-\frac{1}{2} \cdot t-1\right) \cdot \mathrm e^{-\frac{1}{2} \cdot t+1}+\mathrm e$ $\quad (t \in \mathbb{R}, 0 \leq t \leq 12)$

Dabei wird die Zeit $t$ in Wochen und die Höhe $h$ in Meter angegeben.

Stelle den Graphen der Funktion $h$ in einem Koordinatensystem dar. Gib die Beobachtungszeit an, nach der die Pflanze eine Höhe von $1\;\text{m}$ erreicht hatte.

(4 BE)

Interpretiere die folgenden Aussagen jeweils im Sachzusammenhang.

$(\text{I})$

$\(h$

$(\text{II})$

$\dfrac{\mathrm{h}(4)-\mathrm{h}(0)}{4} \approx 0,4$

(4 BE)

Durch die Zugabe von Dünger kann das natürliche Pflanzenwachstum beeinflusst werden. Wird die Pflanze zum Zeitpunkt der maximalen Höhenzunahme gedüngt, bleibt die erreichte Wachstumsgeschwindigkeit erfahrungsgemäß drei Wochen lang gleich.
Ermittle den Höhenunterschied in Zentimeter, der sich nach diesen drei Wochen für die gedüngte gegenüber der nicht gedüngten Pflanze ergeben würde.

(5 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Da die $\mathrm e$ -Funktion keine Nullstellen besitzt, folgt mit dem Satz des Nullprodukts, dass $k\cdot x-1=0$ die einzigen Nullstellen von $f_k$ liefert. Es folgt:

$\begin{array}[t]{rll} k\cdot x-1&=&0 &\quad \scriptsize \mid\;+1 \\[5pt] k\cdot x&=&1 &\quad \scriptsize \mid\;:k \\[5pt] x&=&\dfrac{1}{k} \end{array}$

Somit besitzt jeder Graph von $f_k$ als einzigen Schnittpunkt mit der $x$ -Achse den Punkt $S_k\left(\left.\frac{1}{k} \right\rvert\, 0\right).$

Graphen auf lokale Extrempunkte und Wendepunkte untersuchen

Für die ersten drei Ableitungen von $f_k$ folgt mit dem CAS:

$\(f_k$

1. Schritt: Notwendige Bedingung für lokale Extremstellen anwenden

$\(f_k$

Auflösen nach $x$ mit dem solve-Befehl des CAS liefert:

$x=0$

2. Schritt: Hinreichende Bedingung für lokale Extremstellen überprüfen

$\(\begin{array}[t]{rll} f_k$

Somit besitzt jeder Graph von $f_k$ an der Stelle $x=0$ einen Tiefpunkt.

3. Schritt: Koordinaten bestimmen

$\begin{array}[t]{rll} f_k(0)&=&(k\cdot0 - 1)\cdot\mathrm e^{k\cdot0 + 1} \\[5pt] &=&-\mathrm e \end{array}$

Jeder Graph von $f_k$ besitzt somit den Tiefpunkt $T(0\mid-\mathrm e).$

4. Schritt: Notwendige Bedingung für Wendestellen anwenden

$\(f_k$

Auslösen nach $x$ mit dem solve-Befehl des CAS liefert:

$x=-\dfrac{1}{k}$

5. Schritt: Hinreichende Bedingung für Wendestellen überprüfen

Rechenweg anzeigen

$\( f_k$

Somit besitzt jeder Graph von $f_k$ an der Stelle $x=-\frac{1}{k}$ einen Wendepunkt.

6. Schritt: Koordinaten bestimmen

Rechenweg anzeigen

$f_k\left(-\dfrac{1}{k}\right) = -2$

Jeder Graph von $f_k$ besitzt somit den Wendepunkt $W_k\left(-\frac{1}{k}\mid-2\right).$

Einfluss von $\boldsymbol{k}$ beschreiben

Auf die Lage der Tiefpunkte besitzt $k$ keinen Einfluss. Je größer der Betrag von $k$ ist, desto kleiner ist der Abstand der Wendepunkte $W_k$ zur $y$ -Achse und umgekehrt.

Es gilt:

$\begin{array}[t]{rll} f_{-k}(x)&=&((-k)x - 1)\cdot\mathrm e^{(-k)x + 1} \\[5pt] &=&(k\cdot(-x) - 1)\cdot\mathrm e^{k\cdot(-x) + 1} \\[5pt] &=&f_k(-x) \end{array}$

Durch Spiegeln des Graphen von $f_k$ an der $y$ -Achse entsteht somit der Graph von $f_{-k}.$ Da nach Aufgabenteil 1a) die einzige Nullstelle von $f_k$ bei $x=\frac{1}{k}$ liegt, folgt somit:

$\begin{array}[t]{rll} A&=&2\;\text{FE} \\[5pt] -2\cdot\displaystyle\int_{0}^{\frac{1}{k}}f_k(x)\;\mathrm dx&=&2\;\text{FE} \end{array}$

Auslösen nach $k$ mit dem solve-Befehl des CAS liefert für einen gesuchten Wert von $k:$

$\begin{array}[t]{rll} k_1&=&\mathrm e^2-2\mathrm e \\[5pt] k_2&=&2\mathrm e-\mathrm e^2 \end{array}$

Teilung in zwei flächengleiche Dreiecke zeigen

Mit der graphischen Darstellung des CAS folgt, dass das Dreieck $PS_kO$ ein rechtwinkliges Dreieck mit rechtem Winkel im Koordinatenursprung ist. Für die Länge der Seiten $\overline{OS_k}$ und $\overline{PO}$ folgt somit:

$\begin{array}[t]{rll} \left\vert\overline{OS_k}\right\vert&=&\dfrac{1}{k} \\[5pt] \left\vert\overline{PO}\right\vert&=&\mathrm e \end{array}$

Für den Flächeninhalt $A_1$ des Dreiecks $PS_kO$ gilt damit:

$A_1=\dfrac{1}{2}\cdot\dfrac{1}{k}\cdot\mathrm e=\dfrac{\mathrm e}{2k}$

Für die Höhe $h$ zur Grundseite $\overline{PO}$ des Dreiecks $R_kPO$ gilt $h=0-\left(-\frac{1}{k}\right)=\frac{1}{k}.$ Somit folgt für den Flächeninhalt $A_2$ des Dreiecks $R_kPO:$

$\begin{array}[t]{rll} A_2&=&\dfrac{1}{2}\cdot h\cdot\left\vert\overline{PO}\right\vert \\[5pt] &=&\dfrac{1}{2}\cdot\dfrac{1}{k}\cdot\mathrm e \\[5pt] &=&\dfrac{\mathrm e}{2k} \end{array}$

Somit gilt $A_1=A_2,$ das heißt die $y$ -Achse teilt die betrachteten Vierecke für jeden Wert von $k$ in zwei flächengleiche Dreiecke.

Flächeninhalt des Vierecks berechnen

Da die Summe der Innenwinkel eines Dreiecks $180^\circ$ ergibt, gilt in diesem Fall, dass sowohl der Winkel in $S_k$ als auch der Winkel $\sphericalangle OPS_k$ jeweils $45^\circ$ betragen. Damit sind die beiden Seiten $\overline{OS_k}$ und $\overline{PO}$ gleichlang, das heißt für $k$ gilt:

$\begin{array}[t]{rll} \left\vert\overline{PO}\right\vert&=&\left\vert\overline{OS_k}\right\vert \\[5pt] \mathrm e&=&\dfrac{1}{k} &\quad \scriptsize \mid\;\cdot k\\[5pt] \mathrm e \cdot k&=&1 &\quad \scriptsize \mid\;:\mathrm e\\[5pt] k&=&\dfrac{1}{\mathrm e} \end{array}$

Damit folgt für den Flächeninhalt $A$ des gesuchten Vierecks:

$A=2\cdot\dfrac{1}{2}\cdot \mathrm e\cdot\dfrac{\mathrm e}{1}=\mathrm e^2$

$q_k(x)=ax^2+bx+c$

Da die Funktion achsensymmetrisch zur $y$ -Achse ist, das heißt $q_k(x)=q_k(-x)$ gilt, können in $q_k(x)$ nur gerade Exponenten von $x$ vorkommen. Somit folgt $b=0.$ Einsetzen der Koordinaten von $P$ liefert weiter:

$\begin{array}[t]{rll} q_k(0)&=&-\mathrm e \\[5pt] a\cdot0^2+c&=&-\mathrm e \\[5pt] c&=&-\mathrm e \end{array}$

Einsetzen der Koordinaten von $S_k$ in $q_k(x)=ax^2-\mathrm e$ ergibt nun für $a:$

$\begin{array}[t]{rll} q_k\left(\dfrac{1}{k}\right)&=&0 \\[5pt] a\cdot\left(\dfrac{1}{k}\right)^2-\mathrm e&=&0 &\quad \scriptsize \mid\;+\mathrm e \\[5pt] a\cdot\left(\dfrac{1}{k}\right)^2&=&\mathrm e &\quad \scriptsize \mid\;\cdot k^2 \\[5pt] a&=&k^2\mathrm e \end{array}$

Die Funktionsgleichung von $q_k$ ergibt sich somit als $q_k(x)=k^2\mathrm ex^2-\mathrm e.$

Stelle mit maximaler Differenz der Funktionswerte berechnen

Für die Differenzenfunktion $d_k$ der beiden betrachteten Funktionen folgt:

$\begin{array}[t]{rll} d_k(x)&=&q_k(x)-f_k(x) \\[5pt] &=&k^2\mathrm ex^2-\mathrm e-(kx-1) \cdot \mathrm e^{kx+1} \end{array}$

Für die ersten beiden Ableitungen von $d_k$ folgt mit dem CAS:

$\(d_k$

1. Schritt: Notwendige Bedingung für lokale Extremstellen anwenden

$\(d_k$

Auslösen nach $x$ mit dem solve-Befehl des CAS liefert:

$\begin{array}[t]{rll} x_1&=&0 \\[5pt] x_2&=&\dfrac{\ln(2)}{k} \end{array}$

2. Schritt: Hinreichende Bedingung für lokale Extremstellen überprüfen

Da $x_1=0$ nicht im betrachteten Intervall liegt, muss nur $x_2$ betrachtet werden. Es folgt:

Rechenweg anzeigen

$\( d_k$

Die Differenz der Funktionswerte von $q_k$ und $f_k$ ist somit im betrachteten Intervall an der Stelle $x_2=\frac{\ln(2)}{k}$ am größten.

Konstante Differenz zeigen

Rechenweg anzeigen

$d_k\left(\dfrac{\ln(2)}{k}\right) \approx 0,256\;\text{LE}$

Graphen darstellen

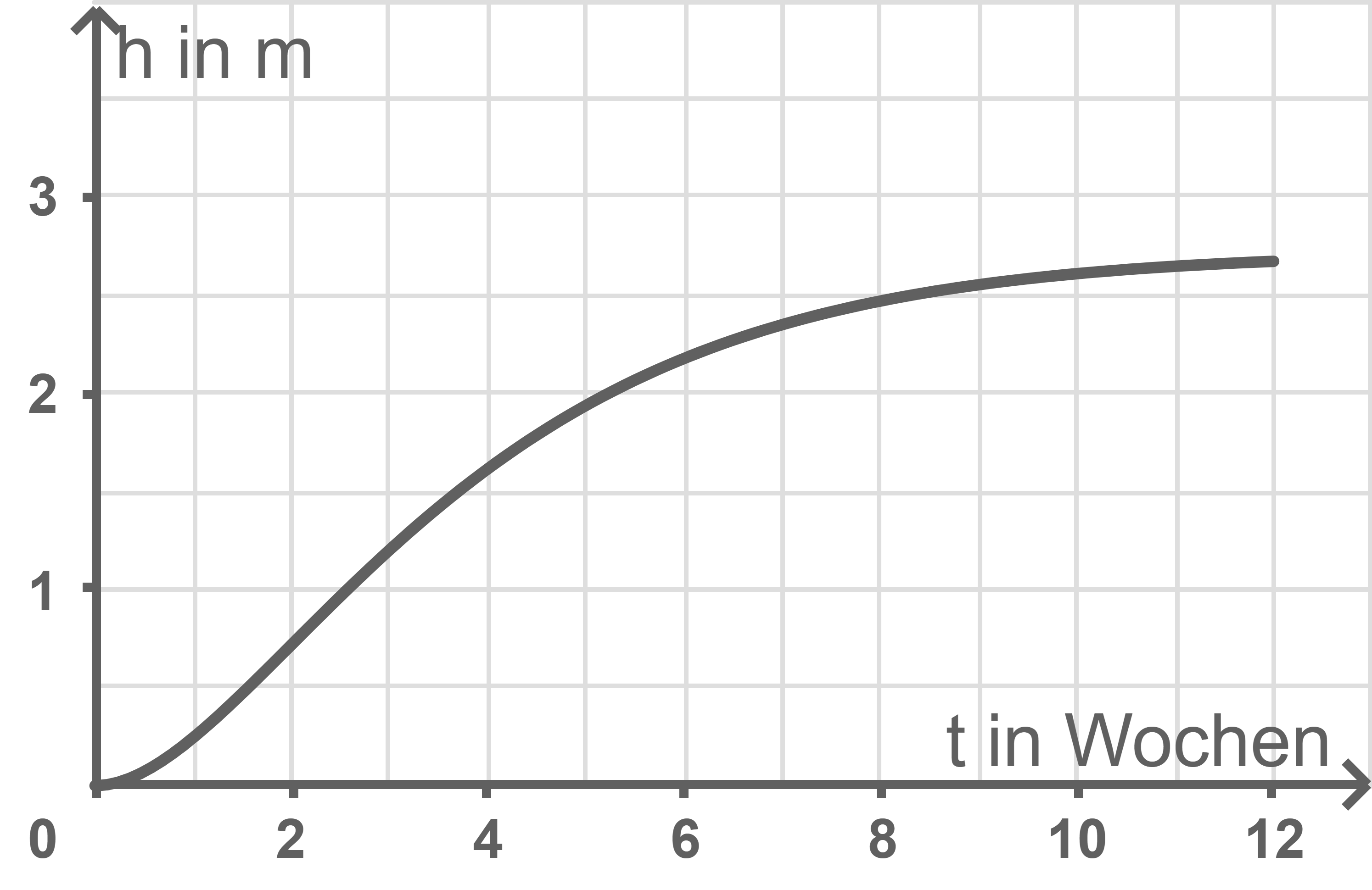Beobachtungszeit angeben

Die Gleichung $h(t)=1$ liefert mit dem solve-Befehl des CAS die gesuchte Lösung $t\approx2,57.$ Die Beobachtungszeit, nach der die Pflanze eine Höhe von $1\;\text{m}$ erreicht hatte, beträgt somit ca. $2,57$ Wochen.

$(\text{I}):$

Die Wachstumsgeschwindigkeit ist kleiner als $0,6\;\text{m}$ pro Woche.

$(\text{II}):$

In den ersten vier Wochen beträgt die mittlere Wachstumsgeschwindigkeit etwa $0,4\;\text{m}$ pro Woche.

Der Zeitpunkt der maximalen Höhenzunahme ist die Stelle, an der der Graph der Funktion $h$ einen Wendepunkt von einer Links- in eine Rechtskrümmung besitzt. Bestimmen der Koordinaten dieses Punktes mit der graphischen Darstellung des CAS liefert $W(2\mid \mathrm e-2).$ Mit Hilfe des CAS folgt für die erste Ableitung von $h:$

$\(h$

Für die Wachstumsgeschwindigkeit an der Stelle $x=2$ gilt somit:

$\(\begin{array}[t]{rll} h$

Da diese Wachstumsgeschwindigkeit bei der gedüngten Pflanze für drei Wochen gleich bleibt, wird die Höhe dieser nach diesem Zeitraum durch den Term $h(2)+3\cdot\frac{1}{2}$ beschrieben. Somit folgt für die gesuchte Höhendifferenz $d$ der gedüngten Pflanze zur ungedüngten Pflanze nach dem Ende der gleichbleibenden Wachstumsgeschwindigkeit:

Rechenweg anzeigen

$d \approx 0,28\;[\text{m}]$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?