Teil C2

Im März 2018 wurde eine Online-Umfrage zum Thema Plastikmüll durchgeführt.

Nach: https:\\de.statista.com (29.06.2021)

Es beantworteten 1016 Personen, die eine Plastiktüte beim Einkauf erhielten, die Frage „Wie oft verwenden Sie eine Plastiktüte üblicherweise?“.

Einige Ergebnisse der Befragung sind in folgender Tabelle dargestellt.

Häufigkeit der Nutzung	Anteil der befragten Personen
einmal	$16 \;\%$
zwei- bis viermal	$37 \;\%$
fünf- bis siebenmal	$15 \;\%$
acht- bis zehnmal	$7 \;\%$
mehr als zehnmal

Berechne die Anzahl der Personen, die eine Plastiktüte üblicherweise sogar mehr als zehnmal nutzen.

Stelle die Anteile in einem Säulendiagramm dar.

(3 BE)

Die Anzahl der Personen, die eine Plastiktüte mehr als einmal benutzen, soll modellhaft als binomialverteilt angenommen werden.

In einem Modegeschäft lassen sich 50 Personen die Ware in Plastiktüten einpacken.

Bestimme die Wahrscheinlichkeit folgender Ereignisse:

A: = „Genau 15 dieser Personen werden ihre Plastiktüte bereits nach diesem Einkauf wegwerfen.“

B:= „Höchstens $10\;\%$ der Käufer werden diese Plastiktüten nicht noch einmal verwenden.“

(4 BE)

Für $n=100$ ist folgende Grafik gegeben:

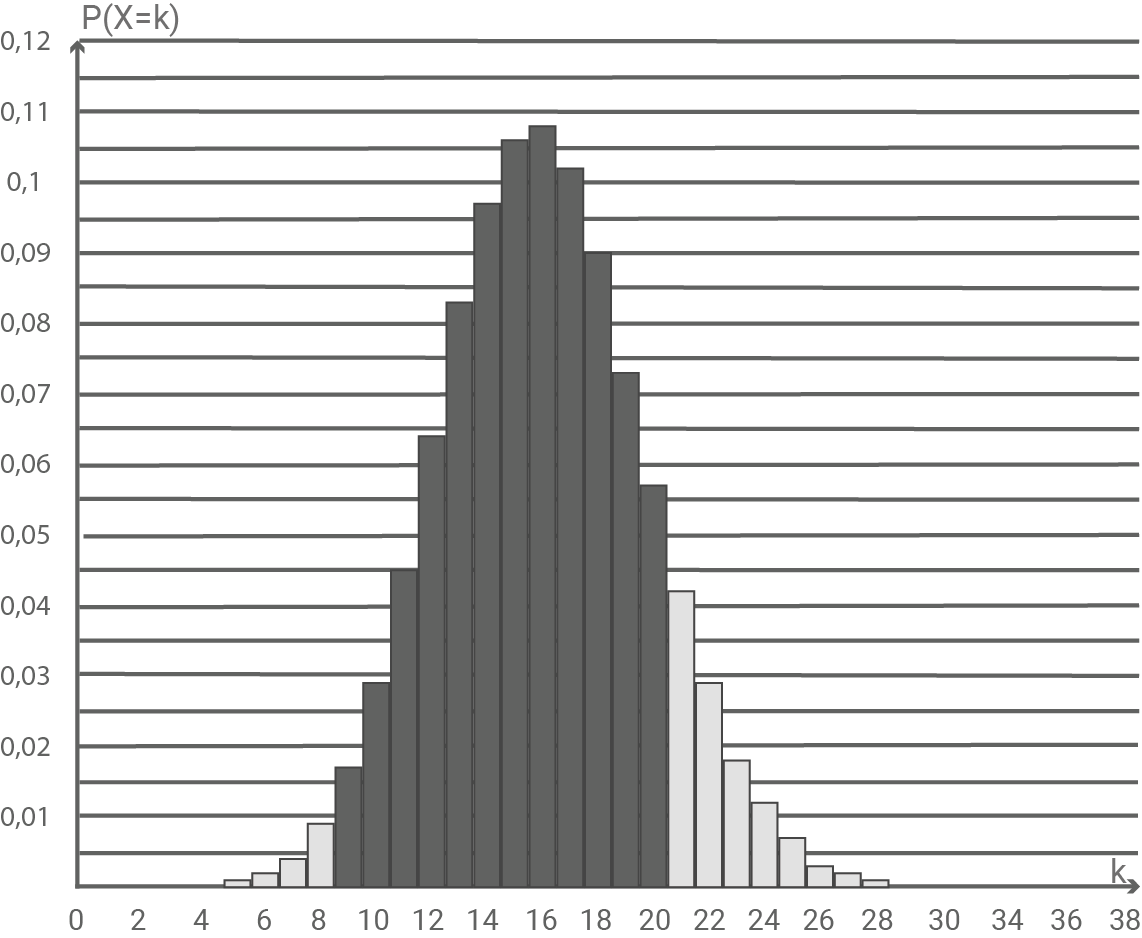
Beschreibe im Sachzusammenhang ein Ereignis C für die in der Grafik grau markierten Fläche.

Gib einen Term zur Berechnung der Wahrscheinlichkeit dieses Ereignisses mit Hilfe des Summenzeichens an.

(4 BE)

Die angegebene Binomialverteilung soll durch eine Normalverteilung mit $\mu=16$ und $\sigma=3,67$ approximiert werden.
Das Ereignis D gibt an, dass mindestens 14 Personen ihre Plastiktüte nur einmal verwenden.

Berechne die Differenz der Wahrscheinlichkeiten des Ereignisses D nach dem Modell der Binomialverteilung und dem Modell der Normalverteilung.

(4 BE)

Eine Schülergruppe plant unter den 120 Lernenden der Oberstufe ihrer Schule den Anteil derer, die Plastiktüten mehrfach nutzen, zu bestimmen.

Berechne je ein $95 \;\%$ -Prognoseintervall für die Anzahl derer, die Plastiktüten mehrfach nutzen, wenn von

$\text{(I)}$	$84\;\%$ Mehrfachnutzern nach der Onlineumfrage
$\text{(II)}$	$90\;\%$ erwarteten Mehrfachnutzern in der eigenen Schule

ausgegangen wird.

Beschreibe die Bedeutung dieser Prognoseintervalle im Sachzusammenhang.

Bei einem Stichprobenumfang von 120 Personen ergab eine Befragung 105 Mehrfachnutzer.

Begründe, dass dieses Ergebnis nicht eindeutig einem der Anteile $0,84$ oder $0,9$ zugeordnet werden kann.

(7 BE)

Die $95\;\%$ -Prognoseintervalle für die relativen Häufigkeiten der Mehrfachnutzer für $84\;\%$ und $90\;\%$ sollen sich nicht überschneiden.

Berechne den Stichprobenumfang, der dafür mindestens notwendig ist.

(3 BE)

Gegeben ist die Ebene $\epsilon_1$ durch $2x+5z=10$

Berechne die Koordinaten der Durchstoßpunkte der $x$ -Achse und der $z$ -Achse durch $\epsilon_1$ .

Beschreibe die besondere Lage der Ebene $\epsilon_1$ .

Der Punkt $P(-5 \mid 2 \mid z)$ liegt in der Ebene $\epsilon_1$ .

Gib den Wert für $z$ an.

(4 BE)

Die Ebene $\mu$ entsteht durch Spiegelung von $\epsilon_1$ an der $xy$ -Ebene.
Die Ebene $\eta$ entsteht durch Verschiebung von $\epsilon_1$ um eine Einheit entlang der positiven $z$ -Achse.

Bestimme je eine Gleichung für $\mu$ und $\eta$ .

(4 BE)

Gegeben ist die Schar von Ebenen $\epsilon_a$ durch $2x+(a-1)y+5z=10 \;\; (a \in \mathbb{R}).$

Berechne den Abstand des Koordinatenursprungs von $\epsilon_1$ .

Begründe, dass der Koordinatenursprung von keiner anderen Ebene $\epsilon_a$ einen größeren Abstand besitzt.

(4 BE)

Zu $\epsilon_2$ gibt es eine senkrechte Ebene der Schar $\epsilon_a$ .

Bestimme für diese Ebene den Wert von $a$ .

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Der Anteil der befragten Personen, die eine Plastiktüte häufiger als zehnmal nutzen, beträgt $25\%.$ Somit ergibt sich die gesuchte Anzahl der Personen zu $0,25\cdot 1016= 254$

$P ( A )= B _{50 ; 0,16}( X =15) \approx 0,0058$

$P ( B )= B _{50 ; 0,16}( X \leq 5) \approx 0,1677$

Von 100 Personen nutzen 10 bis 20 Personen die Plastiktüte nur ein einziges Mal. $P(C)=\sum_{k=10}^{20}\left(\begin{array}{c} 100 \\ k \end{array}\right) 0,16^k \cdot 0,84^{100-k}$

Die Zufallsvariable $X$ ist binomialverteilt mit $n=100$ und $p=0,16.$

$P(D)=B_{100 ; 0,16}(X \geq 14) \approx 0,7469$

Die Zufallsvariable $Y$ ist normalverteilt mit $\mu=16$ und $\sigma=3,67.$

$P(D)=N_{16 ; 3,67}(Y \geq 14) \approx 0,7071$

Die Differenz beträgt $0,7469-0,7071=0,0398.$

Prognoseintervall für $84\,\%:[93 ; 108]$

Prognoseintervall für $90\,\%$ : $[102 ; 114]$

Geht man von $84\,\%$ Mehrfachnutzern aus, werden mit einer Wahrscheinlichkeit von $95\,\%$ 93 bis 108 von 120 Lernenden angeben, Plastiktüten mehrfach zu nutzen.
Geht man von $90\,\%$ Mehrfachnutzern aus, werden mit einer Wahrscheinlichkeit von $95\,\%$ 102 bis 114 von 120 Lernenden angeben, Plastiktüten mehrfach zu nutzen.

105 liegt in den Prognoseintervallen beider Anteile.

$0,84+2 \cdot \sqrt{\frac{0,84 \cdot 0,16}{n}}$ $\lt 0,9-2 \cdot \sqrt{\frac{0,9 \cdot 0,1}{n}}$

Daraus ergibt sich $n>493,$ also ist mindestens ein Stichprobenumfang von 494 notwendig.

Die Koordianten der Durchstoßpunkte ergeben sich als $S_x(5 \mid 0 \mid 0)$ und $S_z(0\mid 0 \mid 2)$

$\varepsilon_1$ liegt parallel zur $y$ -Achse.

$z=4$

$\mu: 2 x-5 z=10$

Die Ebene $\eta$ muss den Punkt $\(P$ enthalten. Es folgt:

$\begin{array}[t]{rll} 2x +5z&=& c \\[5pt] 2\cdot (-5) +5\cdot 5&=& 15 \end{array}$

$\eta: 2 x+5 z=15$

$d_1= \left| \dfrac{0-10}{\sqrt{2^2+5^2}} \right|=10 \cdot \frac{\sqrt{29}}{29} \;\text{[LE]}$

Der Abstand von $\varepsilon_a$ zum Ursprung ergibt sich zu $d_a=\frac{10}{\sqrt{29+(a-1)^2}}.$

$29+(a-1)^2$ ist eine quadratische Funktion, die ihr Minimum in $a=1$ annimmt. Da die quadratische Funktion im Nenner steht und die Wurzelfunktion monoton ist, entspricht der Abstand, der sich für $a=1$ ergibt, dem maximalen Abstand.

Für $a=2$ ergibt sich ein Normalenvektor zu $\overrightarrow{n_2}=\pmatrix{2 \\ 1 \\ 5}.$

$\overrightarrow{n_a}=\pmatrix{2 \\ a-1 \\ 5}$

Dass die Ebenen orthongonal zueinander sind, muss das Sklarprodukt der Normalenvektoren Null ergeben. Daraus ergibt sich:

$\overrightarrow{n_2} \circ \overrightarrow{n_a}=\pmatrix{2 \\ 1 \\ 5} \circ \pmatrix{2 \\ a-1 \\ 5} =0$

$\begin{array}[t]{rll} 2\cdot 2+a-1+5\cdot 5&=& 0 \\[5pt] 28+a &=& 0&\quad \scriptsize \mid\;-28 \\[5pt] a&=& -28 \end{array}$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?