Teil B2
Auf den Dächern findet man häufig Gauben, in die Fenster eingebaut werden. Eine besondere Form ist die Fledermausgaube. Bei dieser Gaubenart sollte das Verhältnis der Höhe der Gaube zur Gaubenbreite zwischen 1:5 und 1:6 liegen.
Die Randlinie einer solchen Gaube kann modellhaft durch eine Funktion mit
mit 
 beschrieben werden.
beschrieben werden.
Dabei sind und
und  die Nullstellen von
die Nullstellen von 
Die Werte von und
und  sind Längen in Meter.
sind Längen in Meter.
Die Randlinie einer solchen Gaube kann modellhaft durch eine Funktion
Dabei sind
Die Werte von

a)
Zeige, dass der Graph der Funktion  symmetrisch zur
symmetrisch zur  -Achse verläuft.
-Achse verläuft.
(1 BE)
b)
Untersuche, ob das angegebene Verhältnis der Höhe der Gaube zur Gaubenbreite durch diese Gleichung eingehalten wird.
(2 BE)
c)
An beiden Enden der Gaube sollte das Gefälle nicht größer als  sein.
sein.
Untersuche, ob diese Bedingung erfüllt ist.
Berechne die Stellen, in denen das Gefälle der Randlinie am größten ist.
In die Gaube soll ein parabelförmiges Fenster mit der Höhe Untersuche, ob diese Bedingung erfüllt ist.
Berechne die Stellen, in denen das Gefälle der Randlinie am größten ist.
(4 BE)
d)
Ein Fenster soll eine Breite von  haben.
haben.
Berechne die Größe dieser Fensterfläche.
Berechne die Größe dieser Fensterfläche.
(3 BE)
e)
In die Gaube kann auch ein anderes parabelförmiges Fenster der Höhe  eingebaut werden.
eingebaut werden.
Aus bautechnischen Gründen muss der obere Rand dieses Fensters im Modell unterhalb des Graphen der Funktion mit
mit  liegen. Dieses Fenster soll maximale Breite haben.
liegen. Dieses Fenster soll maximale Breite haben.
Skizziere diesen Sachverhalt.
Berechne die maximale Breite.
Aus bautechnischen Gründen muss der obere Rand dieses Fensters im Modell unterhalb des Graphen der Funktion
Skizziere diesen Sachverhalt.
Berechne die maximale Breite.
(4 BE)
f)
Für jede positive reelle Zahl  ist eine Funktion
ist eine Funktion  gegeben durch
gegeben durch 
 .
Bestimme die Werte für den Parameter
.
Bestimme die Werte für den Parameter  , für das Verhältnis der Höhe der Gaube zur Gaubenbreite zwischen 1:5 und 1:6 eingehalten wird.
, für das Verhältnis der Höhe der Gaube zur Gaubenbreite zwischen 1:5 und 1:6 eingehalten wird.
(3 BE)
g)
In asiatischen Ländern findet man oft Gauben in Pagodenform. In der Abbildung ist zusätzlich zur Randlinie der Fledermausgaube die Randlinie einer solchen Pagodenform dargestellt. Zur Beschreibung der Randlinie der Pagode werden die Graphen zweier Funktionen  und
und  verwendet.
verwendet.
 Erläutere einen Ansatz zum Ermitteln der Funktionsgleichungen.
Erläutere einen Ansatz zum Ermitteln der Funktionsgleichungen.
Gib eine Gleichung für oder
oder  an.
an.

Gib eine Gleichung für
(3 BE)
a)
b)
Die Breite der Gaube wird durch den Abstand der beiden Nullstellen von  gegeben. Für die Nullstellen folgt aus
gegeben. Für die Nullstellen folgt aus  mit dem solve-Befehl des CAS:
mit dem solve-Befehl des CAS:
![\(\begin{array}[t]{rll}
x_1&=&-2 \\[5pt]
x_2&=&2
\end{array}\)](https://mathjax.schullv.de/8e4ccfc6500062e6dc2760706316ea9dfa1bac3de91032b825db063a2af7c1e7?color=5a5a5a) Die Breite der Gaube beträgt somit
Die Breite der Gaube beträgt somit ![\(b=x_2-x_1=4\;[\text{m}].\)](https://mathjax.schullv.de/b71005bd392cb5a7ecc1d270c222cbb327beadc64d282ac7dc3ca11b15573c4b?color=5a5a5a)
Mit der graphischen Darstellung von im CAS ergibt sich das Maximum von
im CAS ergibt sich das Maximum von 
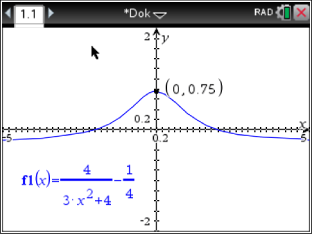 Der
Der  -Wert des Maximums, und damit der Wert, welcher die Höhe der Gaube angibt, beträgt somit
-Wert des Maximums, und damit der Wert, welcher die Höhe der Gaube angibt, beträgt somit  Für das Verhältnis der Höhe zur Breite folgt:
Für das Verhältnis der Höhe zur Breite folgt:
![\(\begin{array}[t]{rll}
\dfrac{h}{b}&=& \dfrac{0,75}{4} \\[5pt]
&=& 0,1875
\end{array}\)](https://mathjax.schullv.de/8a40c6e61c8b9e8183e656de1dda813670780659021a8fea5b980c1b08e5fc01?color=5a5a5a) Mit
Mit  und
und  folgt, dass das Verhältnis der Höhe zu Breite im geforderten Bereich liegt.
folgt, dass das Verhältnis der Höhe zu Breite im geforderten Bereich liegt.
Mit der graphischen Darstellung von

c)
Gefälle der Gaube an den Enden untersuchen
Für die erste Ableitung von  folgt mit dem CAS:
folgt mit dem CAS:
 Da
Da  symmetrisch zur
symmetrisch zur  -Achse ist und die Nullstellen gleichen Abstand zur
-Achse ist und die Nullstellen gleichen Abstand zur  -Achse besitzen, reicht es das Gefälle nur bei beispielsweise
-Achse besitzen, reicht es das Gefälle nur bei beispielsweise  zu bestimmen. Mit dem CAS folgt:
zu bestimmen. Mit dem CAS folgt:
 Für den Steigungswinkel liefert der CAS:
Für den Steigungswinkel liefert der CAS:
![\(\begin{array}[t]{rll}
\tan (\alpha)&=&0,1875 \\[5pt]
\alpha&=& \tan^{-1}(0,1875)\\[5pt]
&\approx& 10,62^\circ \lt 12^\circ
\end{array}\)](https://mathjax.schullv.de/0ce806af5d9219b6ce7dd9e7792f7058391ced9ae21cfc67ee42c7466fb6999d?color=5a5a5a) Die Bedingung ist somit erfüllt.
Stellen mit dem größten Gefälle berechnen
Die Stellen mit dem größten Gefälle entsprechen den Wendestellen des Graphen von
Die Bedingung ist somit erfüllt.
Stellen mit dem größten Gefälle berechnen
Die Stellen mit dem größten Gefälle entsprechen den Wendestellen des Graphen von  Für die zweite und dritte Ableitung von
Für die zweite und dritte Ableitung von  folgt mit dem CAS:
folgt mit dem CAS:

 1. Schritt: Notwendige Bedingung für Extremstellen anwenden
1. Schritt: Notwendige Bedingung für Extremstellen anwenden
 Der solve-Befehl des CAS liefert:
Der solve-Befehl des CAS liefert:
![\(\begin{array}[t]{rll}
x_3&=&-\dfrac{2}{3} \\[5pt]
x_4&=&\dfrac{2}{3}
\end{array}\)](https://mathjax.schullv.de/2310918365d84b4f919e100ae17ce9753b9272ebcf52c7ef97f8b82f315e868d?color=5a5a5a) 2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
Einsetzen von
2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
Einsetzen von  und
und  in
in  liefert mit dem CAS:
liefert mit dem CAS:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/8c149b25437969bf6efeda9167ff25be058bde5f9f8f7ee853689fabf9b0bf99?color=5a5a5a) Die Stellen mit dem größten Gefälle befinden sich somit bei
Die Stellen mit dem größten Gefälle befinden sich somit bei  und
und 
d)
Schritt 1: Parabelgleichung bestimmen
Da  gilt, ist die Parabel symmetrisch zur
gilt, ist die Parabel symmetrisch zur  -Achse. Das gesamte Fenster ist
-Achse. Das gesamte Fenster ist  breit, somit liegen die Nullsten von
breit, somit liegen die Nullsten von  bei
bei  und
und  Einsetzen von z.B.
Einsetzen von z.B.  in
in  liefert:
liefert:
![\(\begin{array}[t]{rll}
p(1)&=&0 \\[5pt]
c\cdot 1^2+0,5&=& 0\scriptsize &\quad \mid\; -0,5 \\[5pt]
c&=& -0,5
\end{array}\)](https://mathjax.schullv.de/f522ba5c5b43e45f8e3756ec341c3b1fe1a46ea5e0fd548a7f85258729e8e65d?color=5a5a5a) Die Gleichung der Parabel ist somit gegeben durch
Die Gleichung der Parabel ist somit gegeben durch  Schritt 2: Flächeninhalt berechnen
Für die Größe
Schritt 2: Flächeninhalt berechnen
Für die Größe  der Fensterfläche folgt mit dem CAS:
der Fensterfläche folgt mit dem CAS:
![\(\begin{array}[t]{rll}
A&=&\displaystyle\int_{x_1}^{x_2}p(x)\;\mathrm dx \\[5pt]
&=&\displaystyle\int_{-1}^{1}(-0,5x^2 + 0,5)\;\mathrm dx \\[5pt]
&\approx&0,67\;[\text{m}^2]
\end{array}\)](https://mathjax.schullv.de/837917f6b8770d620a5ea1bbe2bb0ce4a5245ef7bf4419a515e1aeb1d8aed1a6?color=5a5a5a)
e)
Sachverhalt skizzieren
Für ein Fenster mit maximaler Breite muss der Graph von  den Graphen von
den Graphen von  berühren. Es folgt:
berühren. Es folgt:
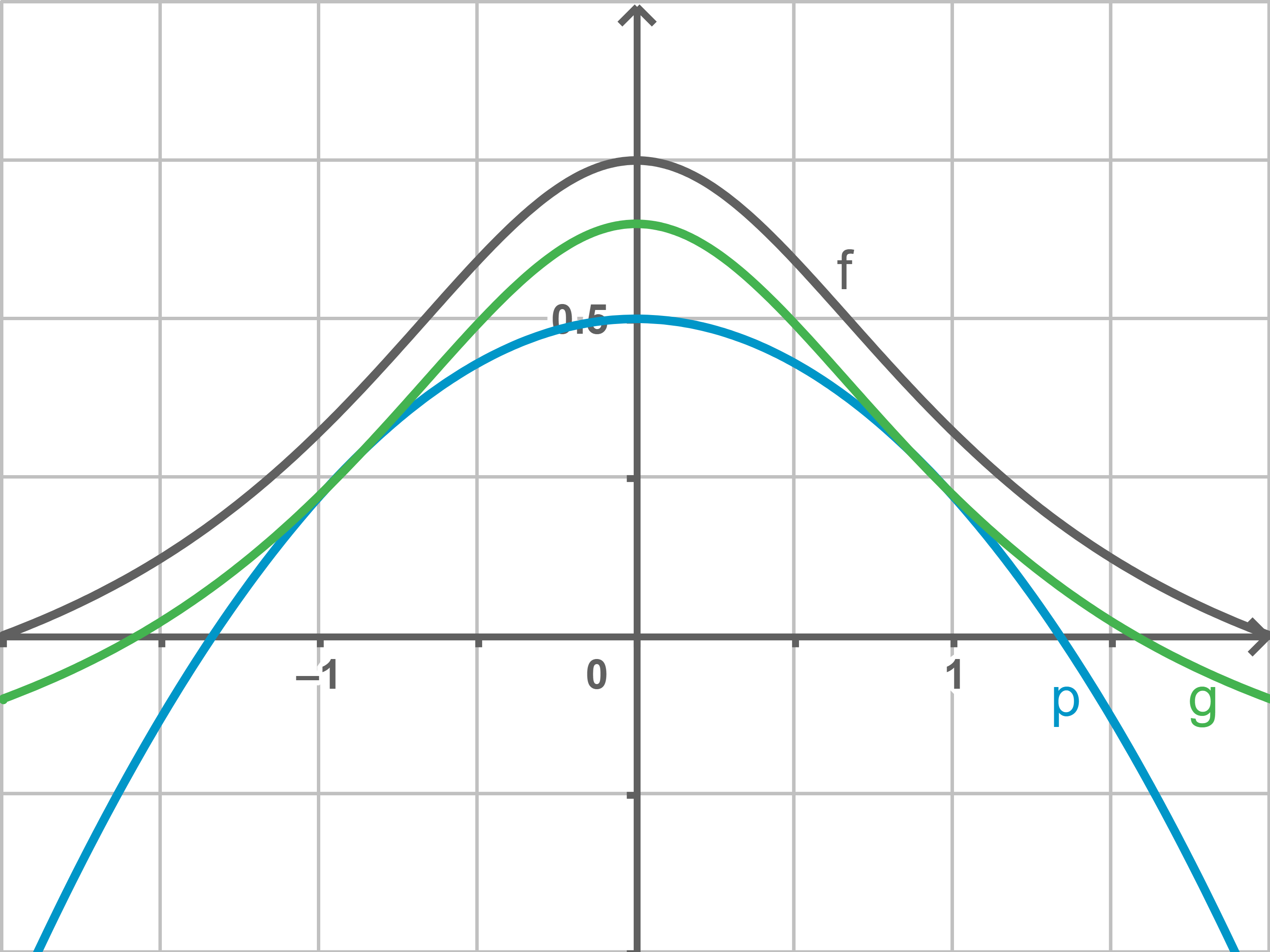 Maximale Breite berechnen
Die Graphen von
Maximale Breite berechnen
Die Graphen von  und
und  berühren sich in zwei Punkten, an denen somit
berühren sich in zwei Punkten, an denen somit  und
und  gilt. Es ergibt sich folgendes Gleichungssystem:
gilt. Es ergibt sich folgendes Gleichungssystem:
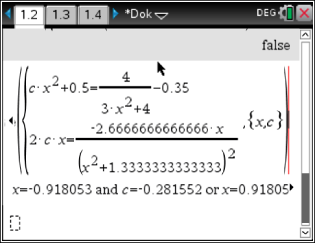 Die neue Parabel
Die neue Parabel  ist somit gegeben durch
ist somit gegeben durch  Mit Hilfe des solve-Befehls des CAS folgt für die Nullstellen:
Mit Hilfe des solve-Befehls des CAS folgt für die Nullstellen:
![\(\begin{array}[t]{rll}
x_1&\approx&-1,33 \\[5pt]
x_2&\approx&1,33
\end{array}\)](https://mathjax.schullv.de/11040324298e6a6cef8805344109595b9f3d81786f4e3d573b1b086834d6ac6c?color=5a5a5a) Die maximale Fensterbreite ergibt sich somit durch den Abstand der Nullstellen als ca.
Die maximale Fensterbreite ergibt sich somit durch den Abstand der Nullstellen als ca. 


Lösen des Gleichungssystems mit dem CAS liefert:
![\(\begin{array}[t]{rll}
c&\approx&0,28 \\[5pt]
x_{L_1}&\approx&-0,918 \\[5pt]
x_{L_2}&\approx&0,918
\end{array}\)](https://mathjax.schullv.de/e3c55ca33d79bad925da40e20dea873eaa0e4f05a9d35a56f1b4a75cb71bc850?color=5a5a5a)

f)
Schritt 1: Verhältnis berechnen
Die Höhe und Breite ergibt sich analog zu Aufgabenteil b). Die Funktionen  sind wieder symmetrisch zur
sind wieder symmetrisch zur  -Achse und besitzen ihren Hochpunkt bei
-Achse und besitzen ihren Hochpunkt bei  Für die Höhe folgt somit:
Für die Höhe folgt somit:

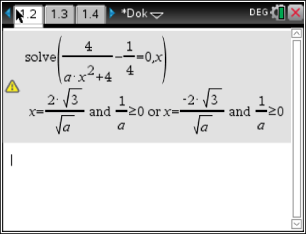 Damit ergibt sich für das Verhältnis zwischen Höhe und Breite:
Damit ergibt sich für das Verhältnis zwischen Höhe und Breite:
![\(\begin{array}[t]{rll}
\dfrac{h}{b}&=&\dfrac{3}{4}\cdot \dfrac{\sqrt{a}}{4\cdot \sqrt{3}} \\[5pt]
&=&\dfrac{\sqrt{3} \sqrt{a}}{16}
\end{array}\)](https://mathjax.schullv.de/a38229948d80f755eef861222ca463ff40b86b0e7954b9482544eaff251bd447?color=5a5a5a) Schritt 2: Werte für
Schritt 2: Werte für  bestimmen
Damit das Verhältnis eingehalten wird, muss folgende Ungleichung erfüllt sein:
bestimmen
Damit das Verhältnis eingehalten wird, muss folgende Ungleichung erfüllt sein:
 Mit dem solve-Befehl des CAS folgt:
Mit dem solve-Befehl des CAS folgt:
 Das Verhältnis zwischen Höhe und Breite ist damit für alle Werte
Das Verhältnis zwischen Höhe und Breite ist damit für alle Werte ![\(a \in \left[\frac{64}{27};\frac{256}{75}\right]\)](https://mathjax.schullv.de/e0c6d5025f72acc20f20c1885d4b00d2bcf7aa40c748a44b8ac1867af1e6acf1?color=5a5a5a) erfüllt.
erfüllt.
Die Breite folgt wieder mit Hilfe der Nullstellen der Funktion. Für  liefert der solve-Befehl des CAS:
liefert der solve-Befehl des CAS:
![\(\begin{array}[t]{rll}
x_1&=&\dfrac{2\cdot \sqrt{3}}{\sqrt{a}} \\[5pt]
x_2&=&-\dfrac{2\cdot \sqrt{3}}{\sqrt{a}}
\end{array}\)](https://mathjax.schullv.de/fa9a553f79b9345e315da5d3828b00d97090442bbffbed77954f9e54d5615c46?color=5a5a5a) Für die Breite folgt somit:
Für die Breite folgt somit:


g)
Der Abbildung kann entnommen werden, dass die Graphen der Funktionen  und
und  zusammen drei Punkte mit dem der Funktion
zusammen drei Punkte mit dem der Funktion  gemeinsam haben, nämlich die Nullstellen und den Hochpunkt des Graphen von
gemeinsam haben, nämlich die Nullstellen und den Hochpunkt des Graphen von  :
:


 Die Verläufe der Graphen von
Die Verläufe der Graphen von  und
und  erinnern jeweils an die Form einer Parabel und
erinnern jeweils an die Form einer Parabel und  kann als eine Spiegelung von
kann als eine Spiegelung von  an der
an der  -Achse aufgefasst werden.
Hinweis: Da in der Aufgabenstellung dazu keine weiteren Angaben gemacht werden, ist es auch möglich, dass die zugrungeliegenden Funktionen keine Parabelfunktionen sind. Ein Ansatz über Exponentialfunktionen ist ebenfalls möglich. Im Folgenden wird die Lösung zum Parabelansatz behandelt.
Die allgemeine Funktionsgleichung einer Parabelfunktion in der Scheitelpunktform lautet:
-Achse aufgefasst werden.
Hinweis: Da in der Aufgabenstellung dazu keine weiteren Angaben gemacht werden, ist es auch möglich, dass die zugrungeliegenden Funktionen keine Parabelfunktionen sind. Ein Ansatz über Exponentialfunktionen ist ebenfalls möglich. Im Folgenden wird die Lösung zum Parabelansatz behandelt.
Die allgemeine Funktionsgleichung einer Parabelfunktion in der Scheitelpunktform lautet:
 Es kann davon ausgegangen werden, dass sich der Scheitelpunkt im Punkt
Es kann davon ausgegangen werden, dass sich der Scheitelpunkt im Punkt  befindet. Einsetzen der Koordinaten in
befindet. Einsetzen der Koordinaten in  liefert:
liefert:
 Einsetzen der Koordinaten von
Einsetzen der Koordinaten von  liefert mit dem solve-Befehl des CAS weiter:
liefert mit dem solve-Befehl des CAS weiter:
 Mögliche Gleichungen für
Mögliche Gleichungen für  und
und  sind somit gegeben durch:
sind somit gegeben durch:


a)
b)
Die Breite der Gaube wird durch den Abstand der beiden Nullstellen von  gegeben. Für die Nullstellen folgt aus
gegeben. Für die Nullstellen folgt aus  mit dem solve-Befehl des CAS:
mit dem solve-Befehl des CAS:
![\(\begin{array}[t]{rll}
x_1&=&-2 \\[5pt]
x_2&=&2
\end{array}\)](https://mathjax.schullv.de/8e4ccfc6500062e6dc2760706316ea9dfa1bac3de91032b825db063a2af7c1e7?color=5a5a5a) Die Breite der Gaube beträgt somit
Die Breite der Gaube beträgt somit ![\(b=x_2-x_1=4\;[\text{m}].\)](https://mathjax.schullv.de/b71005bd392cb5a7ecc1d270c222cbb327beadc64d282ac7dc3ca11b15573c4b?color=5a5a5a)
Mit der graphischen Darstellung von im CAS ergibt sich das Maximum von
im CAS ergibt sich das Maximum von 
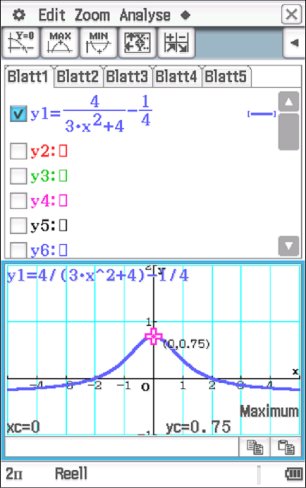 Der
Der  -Wert des Maximums, und damit der Wert, welcher die Höhe der Gaube angibt, beträgt somit
-Wert des Maximums, und damit der Wert, welcher die Höhe der Gaube angibt, beträgt somit  Für das Verhältnis der Höhe zur Breite folgt:
Für das Verhältnis der Höhe zur Breite folgt:
![\(\begin{array}[t]{rll}
\dfrac{h}{b}&=& \dfrac{0,75}{4} \\[5pt]
&=& 0,1875
\end{array}\)](https://mathjax.schullv.de/8a40c6e61c8b9e8183e656de1dda813670780659021a8fea5b980c1b08e5fc01?color=5a5a5a) Mit
Mit  und
und  folgt, dass das Verhältnis der Höhe zu Breite im geforderten Bereich liegt.
folgt, dass das Verhältnis der Höhe zu Breite im geforderten Bereich liegt.
Mit der graphischen Darstellung von

c)
Gefälle der Gaube an den Enden untersuchen
Für die erste Ableitung von  folgt mit dem CAS:
folgt mit dem CAS:
 Da
Da  symmetrisch zur
symmetrisch zur  -Achse ist und die Nullstellen gleichen Abstand zur
-Achse ist und die Nullstellen gleichen Abstand zur  -Achse besitzen, reicht es das Gefälle nur bei beispielsweise
-Achse besitzen, reicht es das Gefälle nur bei beispielsweise  zu bestimmen. Mit dem CAS folgt:
zu bestimmen. Mit dem CAS folgt:
 Für den Steigungswinkel liefert der CAS:
Für den Steigungswinkel liefert der CAS:
![\(\begin{array}[t]{rll}
\tan (\alpha)&=&0,1875 \\[5pt]
\alpha&=& \tan^{-1}(0,1875)\\[5pt]
&\approx& 10,62^\circ \lt 12^\circ
\end{array}\)](https://mathjax.schullv.de/0ce806af5d9219b6ce7dd9e7792f7058391ced9ae21cfc67ee42c7466fb6999d?color=5a5a5a) Die Bedingung ist somit erfüllt.
Stellen mit dem größten Gefälle berechnen
Die Stellen mit dem größten Gefälle entsprechen den Wendestellen des Graphen von
Die Bedingung ist somit erfüllt.
Stellen mit dem größten Gefälle berechnen
Die Stellen mit dem größten Gefälle entsprechen den Wendestellen des Graphen von  Für die zweite und dritte Ableitung von
Für die zweite und dritte Ableitung von  folgt mit dem CAS:
folgt mit dem CAS:

 1. Schritt: Notwendige Bedingung für Extremstellen anwenden
1. Schritt: Notwendige Bedingung für Extremstellen anwenden
 Der solve-Befehl des CAS liefert:
Der solve-Befehl des CAS liefert:
![\(\begin{array}[t]{rll}
x_3&=&-\dfrac{2}{3} \\[5pt]
x_4&=&\dfrac{2}{3}
\end{array}\)](https://mathjax.schullv.de/2310918365d84b4f919e100ae17ce9753b9272ebcf52c7ef97f8b82f315e868d?color=5a5a5a) 2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
Einsetzen von
2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
Einsetzen von  und
und  in
in  liefert mit dem CAS:
liefert mit dem CAS:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/8c149b25437969bf6efeda9167ff25be058bde5f9f8f7ee853689fabf9b0bf99?color=5a5a5a) Die Stellen mit dem größten Gefälle befinden sich somit bei
Die Stellen mit dem größten Gefälle befinden sich somit bei  und
und 
d)
Schritt 1: Parabelgleichung bestimmen
Da  gilt, ist die Parabel symmetrisch zur
gilt, ist die Parabel symmetrisch zur  -Achse. Das gesamte Fenster ist
-Achse. Das gesamte Fenster ist  breit, somit liegen die Nullsten von
breit, somit liegen die Nullsten von  bei
bei  und
und  Einsetzen von z.B.
Einsetzen von z.B.  in
in  liefert:
liefert:
![\(\begin{array}[t]{rll}
p(1)&=&0 \\[5pt]
c\cdot 1^2+0,5&=& 0\scriptsize &\quad \mid\; -0,5 \\[5pt]
c&=& -0,5
\end{array}\)](https://mathjax.schullv.de/f522ba5c5b43e45f8e3756ec341c3b1fe1a46ea5e0fd548a7f85258729e8e65d?color=5a5a5a) Die Gleichung der Parabel ist somit gegeben durch
Die Gleichung der Parabel ist somit gegeben durch  Schritt 2: Flächeninhalt berechnen
Für die Größe
Schritt 2: Flächeninhalt berechnen
Für die Größe  der Fensterfläche folgt mit dem CAS:
der Fensterfläche folgt mit dem CAS:
![\(\begin{array}[t]{rll}
A&=&\displaystyle\int_{x_1}^{x_2}p(x)\;\mathrm dx \\[5pt]
&=&\displaystyle\int_{-1}^{1}(-0,5x^2 + 0,5)\;\mathrm dx \\[5pt]
&\approx&0,67\;[\text{m}^2]
\end{array}\)](https://mathjax.schullv.de/837917f6b8770d620a5ea1bbe2bb0ce4a5245ef7bf4419a515e1aeb1d8aed1a6?color=5a5a5a)
e)
Sachverhalt skizzieren
Für ein Fenster mit maximaler Breite muss der Graph von  den Graphen von
den Graphen von  berühren. Es folgt:
berühren. Es folgt:
 Maximale Breite berechnen
Maximale Breite berechnen
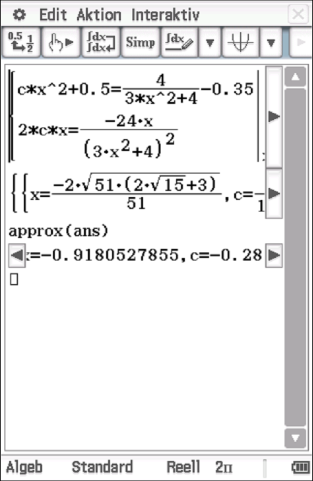 Die neue Parabel
Die neue Parabel  ist somit gegeben durch
ist somit gegeben durch  Mit Hilfe des solve-Befehls des CAS folgt für die Nullstellen:
Mit Hilfe des solve-Befehls des CAS folgt für die Nullstellen:
![\(\begin{array}[t]{rll}
x_1&\approx&-1,33 \\[5pt]
x_2&\approx&1,33
\end{array}\)](https://mathjax.schullv.de/11040324298e6a6cef8805344109595b9f3d81786f4e3d573b1b086834d6ac6c?color=5a5a5a) Die maximale Fensterbreite ergibt sich somit durch den Abstand der Nullstellen als ca.
Die maximale Fensterbreite ergibt sich somit durch den Abstand der Nullstellen als ca. 


Die Graphen von  und
und  berühren sich in zwei Punkten, an denen somit
berühren sich in zwei Punkten, an denen somit  und
und  gilt. Es ergibt sich folgendes Gleichungssystem:
Lösen des Gleichungssystems mit dem CAS liefert:
gilt. Es ergibt sich folgendes Gleichungssystem:
Lösen des Gleichungssystems mit dem CAS liefert:
![\(\begin{array}[t]{rll}
c&\approx&0,28 \\[5pt]
x_{L_1}&\approx&-0,918 \\[5pt]
x_{L_2}&\approx&0,918
\end{array}\)](https://mathjax.schullv.de/e3c55ca33d79bad925da40e20dea873eaa0e4f05a9d35a56f1b4a75cb71bc850?color=5a5a5a)

f)
Schritt 1: Verhältnis berechnen
 Damit ergibt sich für das Verhältnis zwischen Höhe und Breite:
Damit ergibt sich für das Verhältnis zwischen Höhe und Breite:
![\(\begin{array}[t]{rll}
\dfrac{h}{b}&=&\dfrac{3}{4}\cdot \dfrac{\sqrt{a}}{4\cdot \sqrt{3}} \\[5pt]
&=&\dfrac{\sqrt{3} \sqrt{a}}{16}
\end{array}\)](https://mathjax.schullv.de/a38229948d80f755eef861222ca463ff40b86b0e7954b9482544eaff251bd447?color=5a5a5a) Schritt 2: Werte für
Schritt 2: Werte für  bestimmen
Damit das Verhältnis eingehalten wird, muss folgende Ungleichung erfüllt sein:
bestimmen
Damit das Verhältnis eingehalten wird, muss folgende Ungleichung erfüllt sein:
 Mit dem solve-Befehl des CAS folgt:
Mit dem solve-Befehl des CAS folgt:
 Das Verhältnis zwischen Höhe und Breite ist damit für alle Werte
Das Verhältnis zwischen Höhe und Breite ist damit für alle Werte ![\(a \in \left[\frac{64}{27};\frac{256}{75}\right]\)](https://mathjax.schullv.de/e0c6d5025f72acc20f20c1885d4b00d2bcf7aa40c748a44b8ac1867af1e6acf1?color=5a5a5a) erfüllt.
erfüllt.
Die Höhe und Breite ergibt sich analog zu Aufgabenteil b). Die Funktionen  sind wieder symmetrisch zur
sind wieder symmetrisch zur  -Achse und besitzen ihren Hochpunkt bei
-Achse und besitzen ihren Hochpunkt bei  Für die Höhe folgt somit:
Für die Höhe folgt somit:
 Die Breite folgt wieder mit Hilfe der Nullstellen der Funktion. Für
Die Breite folgt wieder mit Hilfe der Nullstellen der Funktion. Für  liefert der solve-Befehl des CAS:
liefert der solve-Befehl des CAS:
![\(\begin{array}[t]{rll}
x_1&=&\dfrac{2\cdot \sqrt{3}}{\sqrt{a}} \\[5pt]
x_2&=&-\dfrac{2\cdot \sqrt{3}}{\sqrt{a}}
\end{array}\)](https://mathjax.schullv.de/fa9a553f79b9345e315da5d3828b00d97090442bbffbed77954f9e54d5615c46?color=5a5a5a) Für die Breite folgt somit:
Für die Breite folgt somit:


g)
Der Abbildung kann entnommen werden, dass die Graphen der Funktionen  und
und  zusammen drei Punkte mit dem der Funktion
zusammen drei Punkte mit dem der Funktion  gemeinsam haben, nämlich die Nullstellen und den Hochpunkt des Graphen von
gemeinsam haben, nämlich die Nullstellen und den Hochpunkt des Graphen von  :
:


 Die Verläufe der Graphen von
Die Verläufe der Graphen von  und
und  erinnern jeweils an die Form einer Parabel und
erinnern jeweils an die Form einer Parabel und  kann als eine Spiegelung von
kann als eine Spiegelung von  an der
an der  -Achse aufgefasst werden.
Hinweis: Da in der Aufgabenstellung dazu keine weiteren Angaben gemacht werden, ist es auch möglich, dass die zugrungeliegenden Funktionen keine Parabelfunktionen sind. Ein Ansatz über Exponentialfunktionen ist ebenfalls möglich. Im Folgenden wird die Lösung zum Parabelansatz behandelt.
Die allgemeine Funktionsgleichung einer Parabelfunktion in der Scheitelpunktform lautet:
-Achse aufgefasst werden.
Hinweis: Da in der Aufgabenstellung dazu keine weiteren Angaben gemacht werden, ist es auch möglich, dass die zugrungeliegenden Funktionen keine Parabelfunktionen sind. Ein Ansatz über Exponentialfunktionen ist ebenfalls möglich. Im Folgenden wird die Lösung zum Parabelansatz behandelt.
Die allgemeine Funktionsgleichung einer Parabelfunktion in der Scheitelpunktform lautet:
 Es kann davon ausgegangen werden, dass sich der Scheitelpunkt im Punkt
Es kann davon ausgegangen werden, dass sich der Scheitelpunkt im Punkt  befindet. Einsetzen der Koordinaten in
befindet. Einsetzen der Koordinaten in  liefert:
liefert:
 Einsetzen der Koordinaten von
Einsetzen der Koordinaten von  liefert mit dem solve-Befehl des CAS weiter:
liefert mit dem solve-Befehl des CAS weiter:
 Mögliche Gleichungen für
Mögliche Gleichungen für  und
und  sind somit gegeben durch:
sind somit gegeben durch:

