Teil A
1
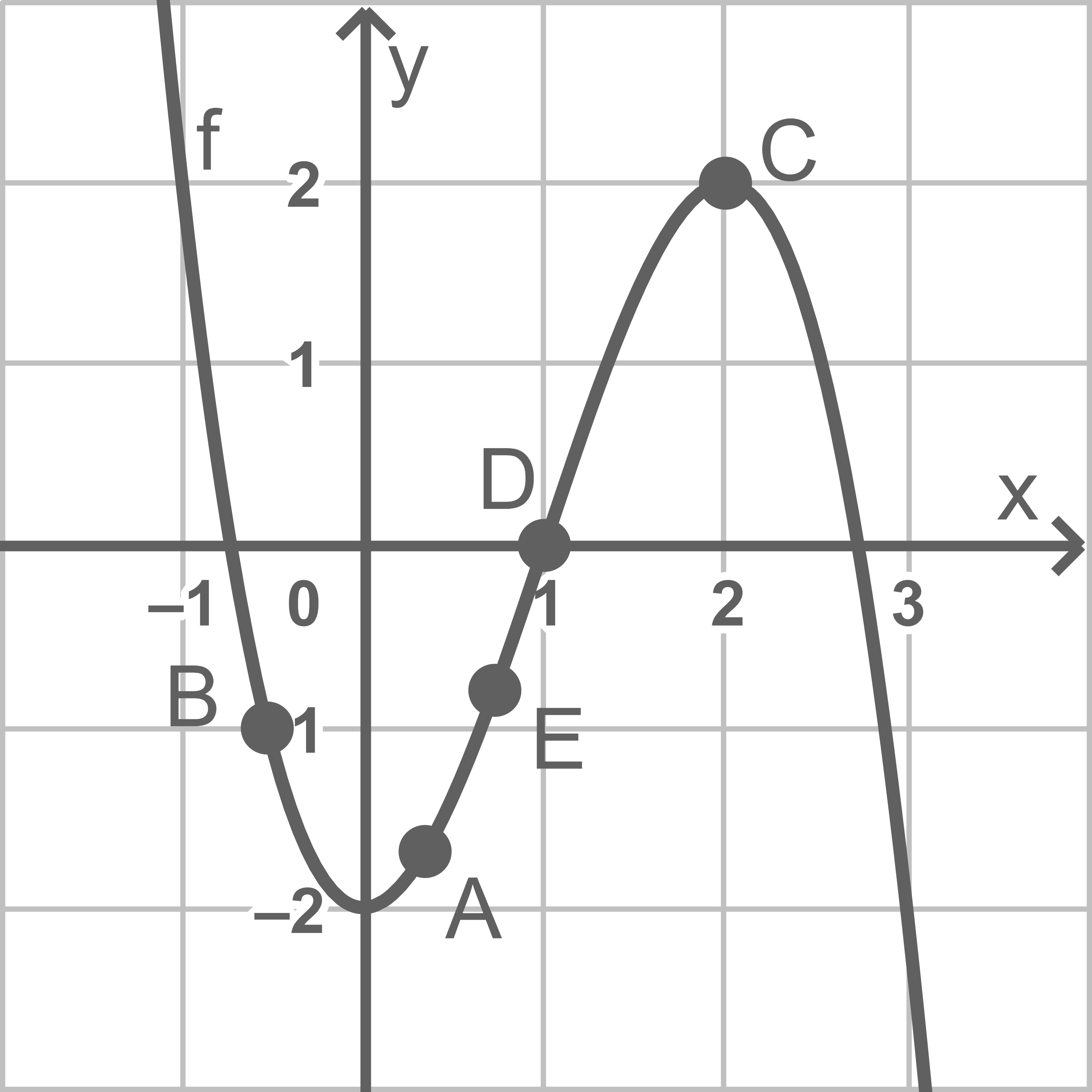
Dargestellt ist der Graph einer Funktion 
Zeichne je einen Punkt mit der folgenden Eigenschaft in die Darstellung ein:
Zeichne je einen Punkt mit der folgenden Eigenschaft in die Darstellung ein:
- Im Punkt
ist der Funktionswert von
negativ.
- Im Punkt
ist die erste Ableitung von
negativ.
- Im Punkt
ist die erste Ableitung von
null.
- Im Punkt
ist die erste Ableitung von
am größten.
- Im Punkt
ist die zweite Ableitung von
positiv.
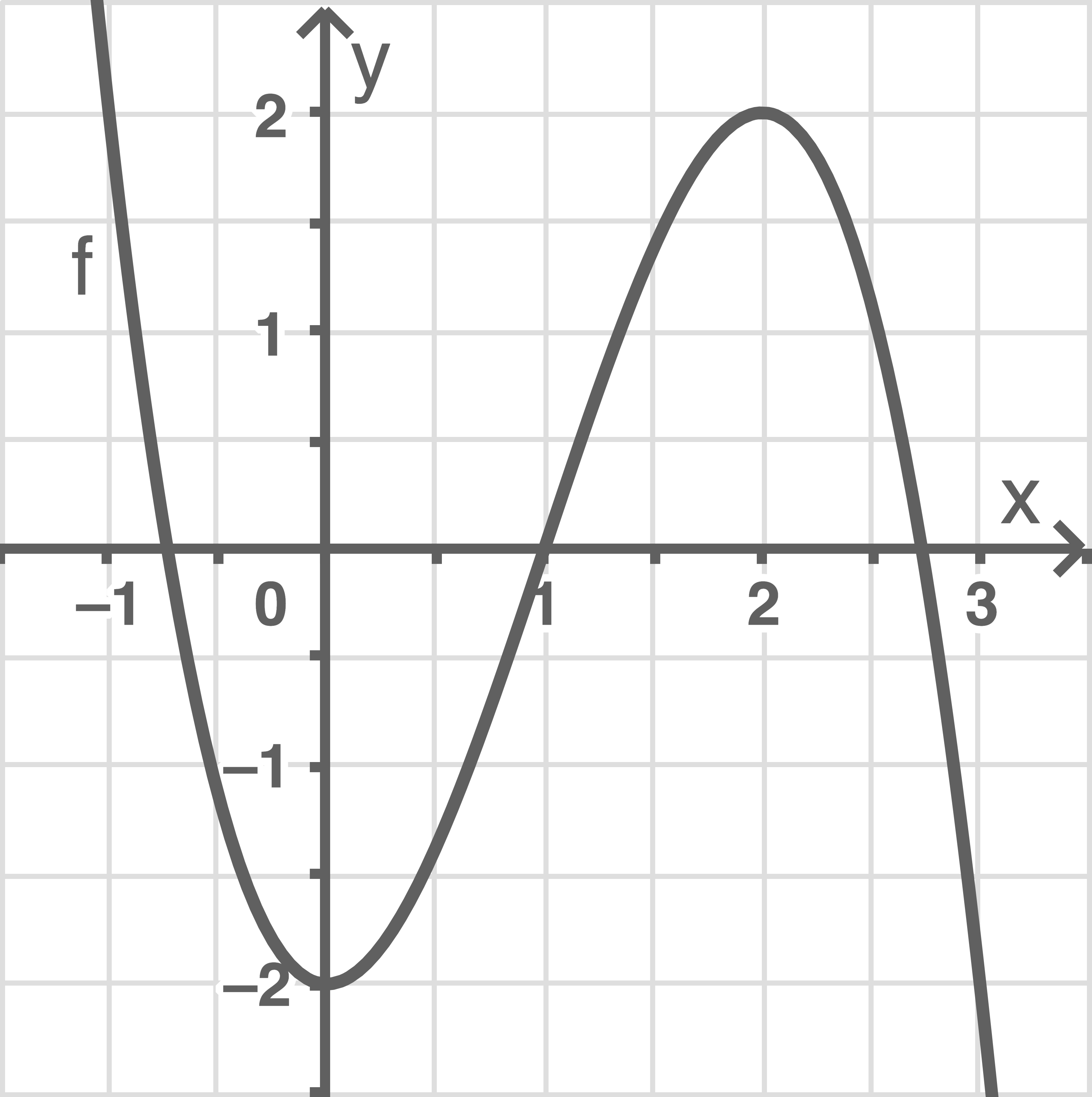
(5 BE)
2
Gegeben ist die Funktion  mit
mit 

Die Abbildung zeigt ihren Graphen , der bei
, der bei  den Wendepunkt
den Wendepunkt  hat.
hat.
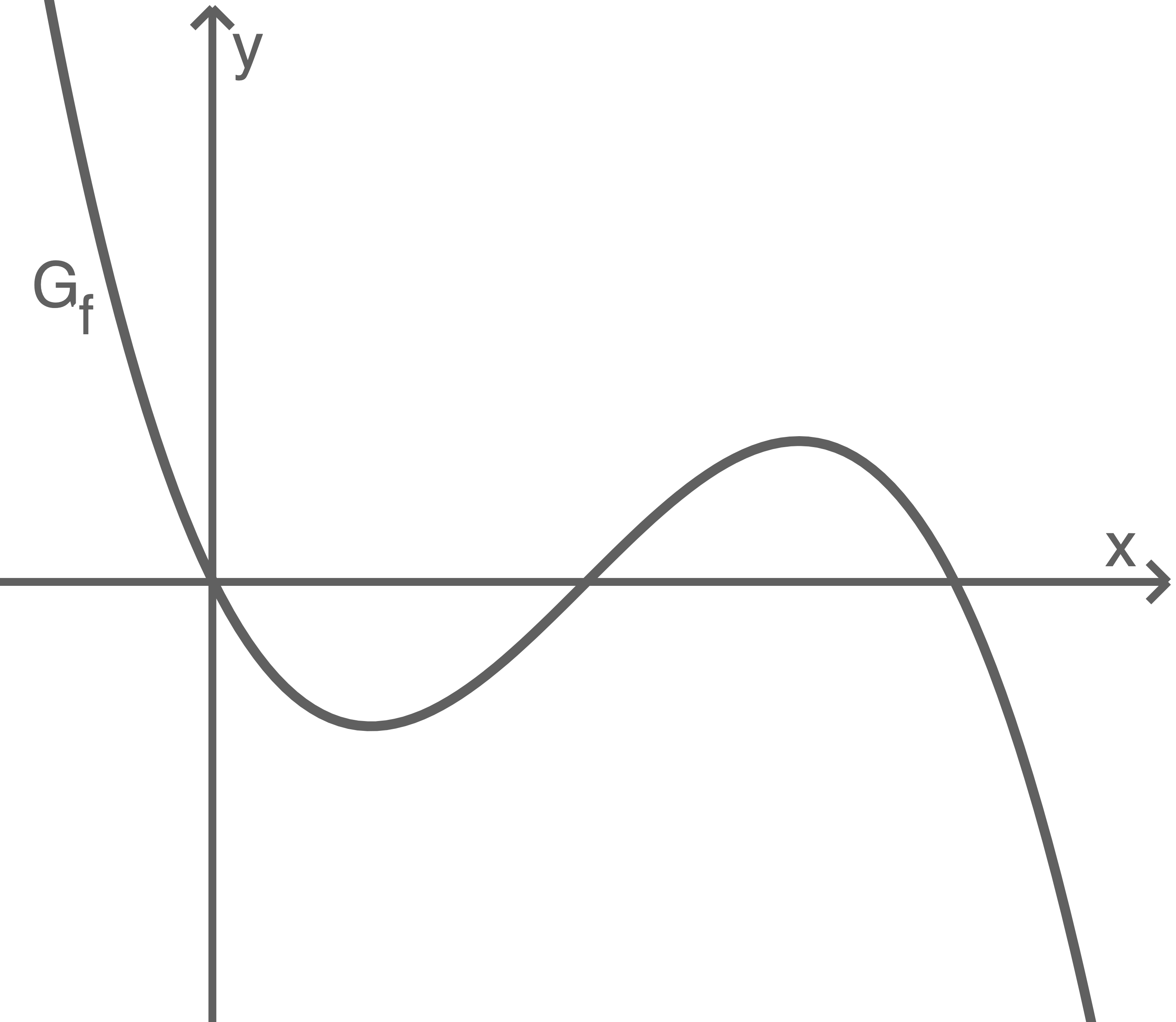
Die Abbildung zeigt ihren Graphen
a)
Zeige, dass die Tangente an  im Punkt
im Punkt  die Steigung 1 hat.
die Steigung 1 hat.
(2 BE)
b)
Betrachtet werden die Geraden mit positiver Steigung  , die durch
, die durch  verlaufen.
verlaufen.
Gib die Anzahl der Schnittpunkte dieser Geraden mit in Abhängigkeit von
in Abhängigkeit von  an.
an.
Gib die Anzahl der Schnittpunkte dieser Geraden mit
(3 BE)

3
Aus einem Tank fließt Wasser langsam ab. Die Abflussrate kann für eine bestimmte Zeit durch die Funktion  mit
mit  beschrieben werden.
(
beschrieben werden.
( : Zeit in Stunden,
: Zeit in Stunden,  : Abflussrate in
: Abflussrate in  )
)
a)
Gib eine Stammfunktion der Funktion  an und erläutere deren Bedeutung für den gegebenen Sachverhalt.
an und erläutere deren Bedeutung für den gegebenen Sachverhalt.
(2 BE)
b)
Der Mittelwert  einer ganzrationalen Funktion im Intervall
einer ganzrationalen Funktion im Intervall  kann mit
kann mit
 berechnet werden.
berechnet werden.
Berechne die mittlere Abflussrate an diesem Tag in den ersten zehn Stunden.
Berechne die mittlere Abflussrate an diesem Tag in den ersten zehn Stunden.
(3 BE)
4
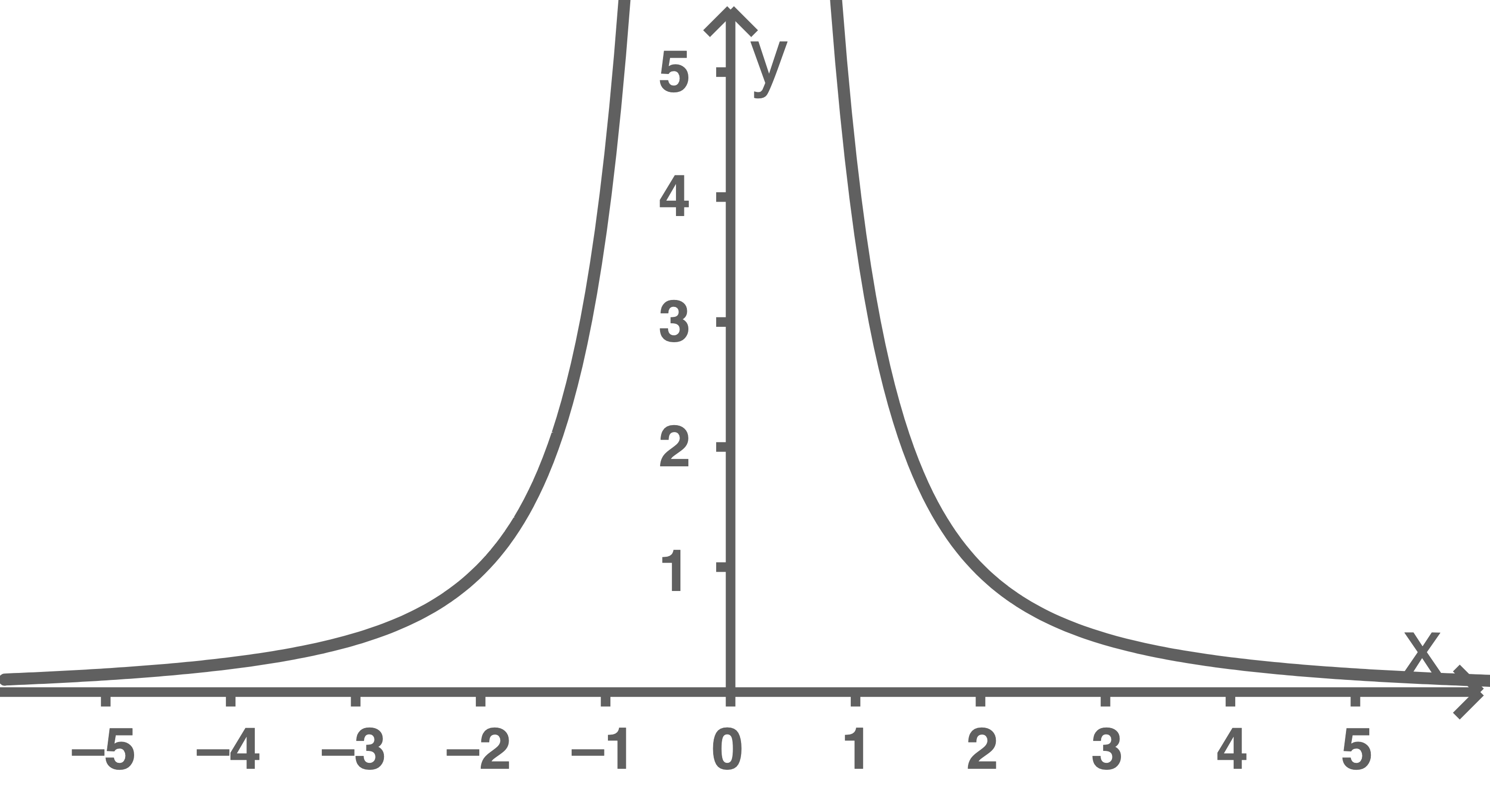
Die Abbildung zeigt den Graphen  der Funktion
der Funktion  mit
mit 
 ,
,  .
.
 ist symmetrisch bezüglich der
ist symmetrisch bezüglich der  -Achse.
-Achse.
a)
Die Gerade, die parallel zur  -Achse durch den Punkt
-Achse durch den Punkt  verläuft, schneidet
verläuft, schneidet  in zwei Punkten. Der Abstand dieser beiden Punkte ist
in zwei Punkten. Der Abstand dieser beiden Punkte ist 
Berechne den Wert von .
.
Berechne den Wert von
(2 BE)
b)
Die Koordinatenachsen schließen mit der Tangente an  in einem Punkt
in einem Punkt  mit
mit  ein gleichschenkliges Dreieck ein.
ein gleichschenkliges Dreieck ein.
Berechne die Koordinaten von .
.
Berechne die Koordinaten von
(3 BE)
5
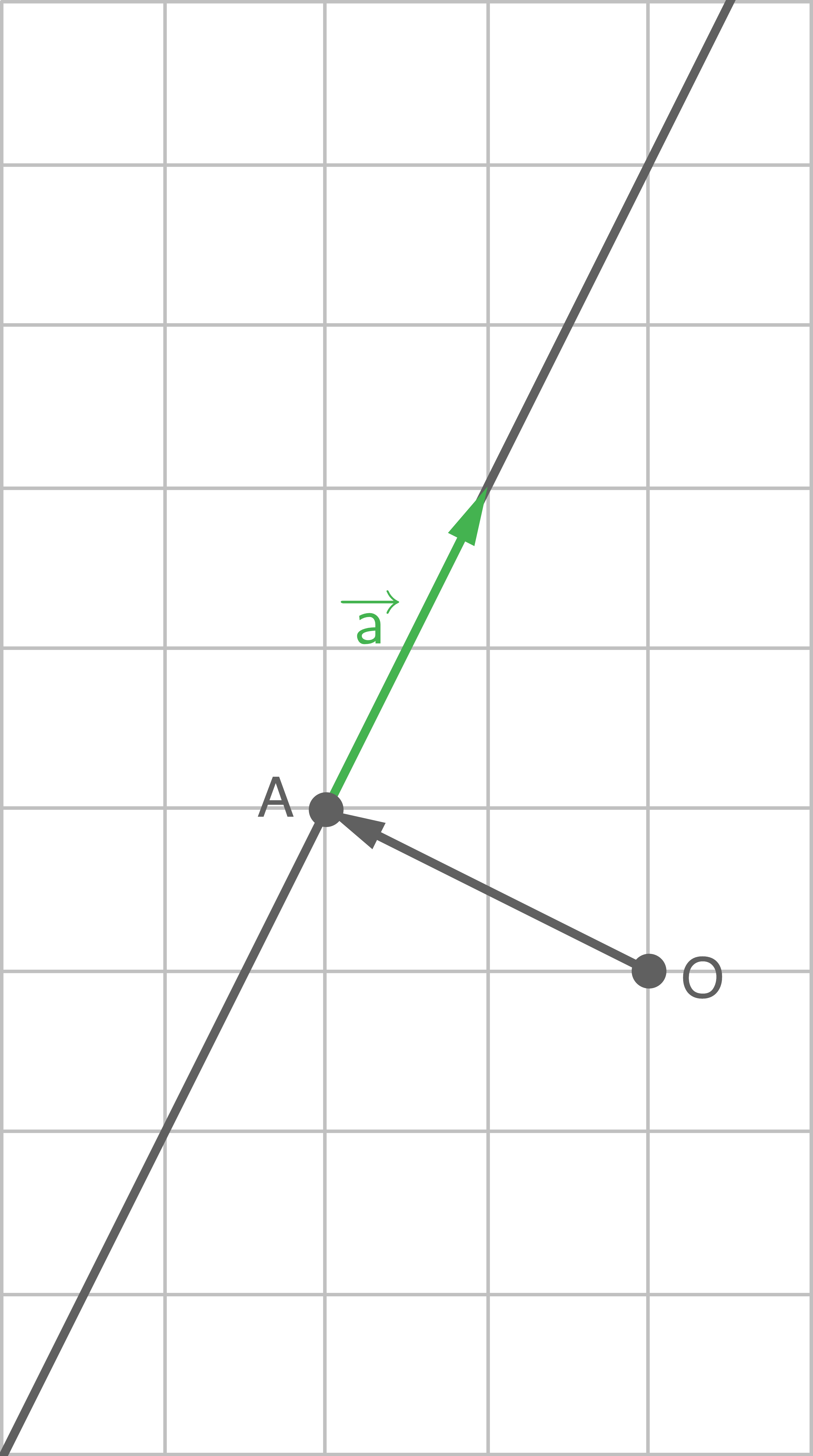
In den Abbildungen ist die Gerade  mit
mit  (
( ).
).
 erhält man den Ortsvektor des Punktes
erhält man den Ortsvektor des Punktes 
 ist das Bild von
ist das Bild von  bei Spiegelung an
bei Spiegelung an  .
.
Gib den zu gehörenden Wert des Parameters
gehörenden Wert des Parameters  an.
an.
a)
Veranschauliche die folgenden Punkte in den Abbildungen:





Für 


(3 BE)
b)
Ein Punkt  teilt die Strecke
teilt die Strecke  im Verhältnis 1:3.
im Verhältnis 1:3.
Gib den zu gehörenden Wert des Parameters
gehörenden Wert des Parameters  an.
an.
Gib den zu
(1 BE)
c)
Gib den zu
(1 BE)
6
Der Punkt  ist Eckpunkt eines Quadrats. Orthogonal zu der Ebene, in der dieses Quadrat liegt, verläuft die Gerade
ist Eckpunkt eines Quadrats. Orthogonal zu der Ebene, in der dieses Quadrat liegt, verläuft die Gerade  mit
mit  .
.
a)
Begründe, dass das Quadrat in der  -Ebene liegt.
-Ebene liegt.
(2 BE)
b)
Der Schnittpunkt der beiden Diagonalen des Quadrats liegt auf der Gerade  , der Punkt
, der Punkt  in der
in der  -Ebene.
-Ebene.
Zeige, dass einer der beiden Eckpunkte des Quadrats ist, die dem Eckpunkt
einer der beiden Eckpunkte des Quadrats ist, die dem Eckpunkt  benachbart sind.
benachbart sind.
Zeige, dass
(3 BE)
7
a)
Die Zufallsgröße  ist binomialverteilt mit
ist binomialverteilt mit  und
und  . Eine der folgenden Abbildungen stellt die Wahrscheinlichkeitsverteilung von
. Eine der folgenden Abbildungen stellt die Wahrscheinlichkeitsverteilung von  dar.
dar.
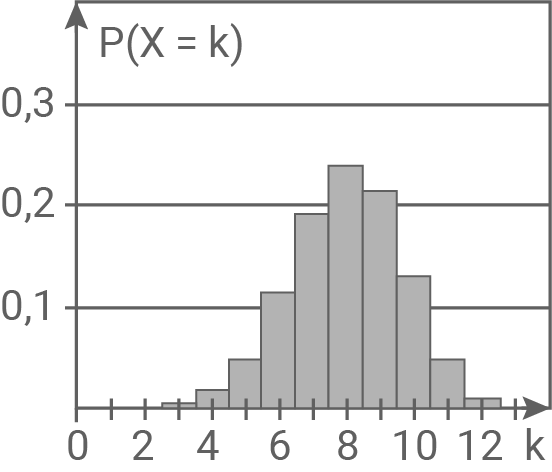
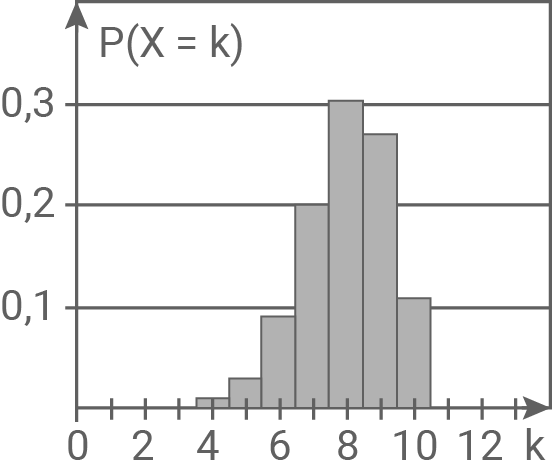
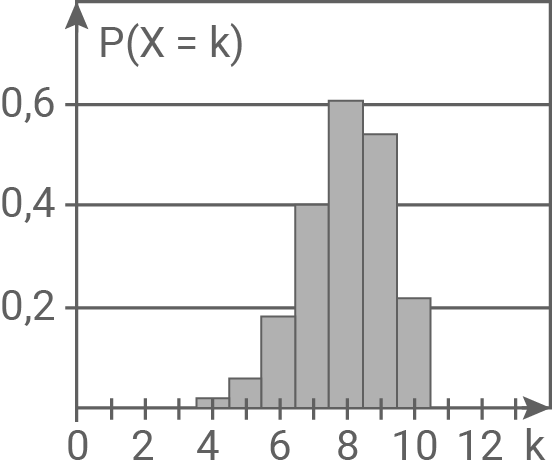 Gib die beiden Abbildungen an, die die Wahrscheinlichkeitsverteilung von
Gib die beiden Abbildungen an, die die Wahrscheinlichkeitsverteilung von  nicht darstellen. Begründe deine Entscheidung.
nicht darstellen. Begründe deine Entscheidung.

Abb. 1

Abb. 2

Abb. 3
(3 BE)
b)
Betrachtet wird die binomialverteilte Zufallsgröße  mit den Parametern
mit den Parametern  und
und  .
Es gilt:
.
Es gilt:
 .
.
- Der Erwartungswert von
ist
- Die Wahrscheinlichkeitsverteilung von
ist symmetrisch.
(2 BE)
8
Es sei  eine normalverteilte Zufallsgröße mit
eine normalverteilte Zufallsgröße mit  mit der dargestellten Dichtefunktion:
mit der dargestellten Dichtefunktion:
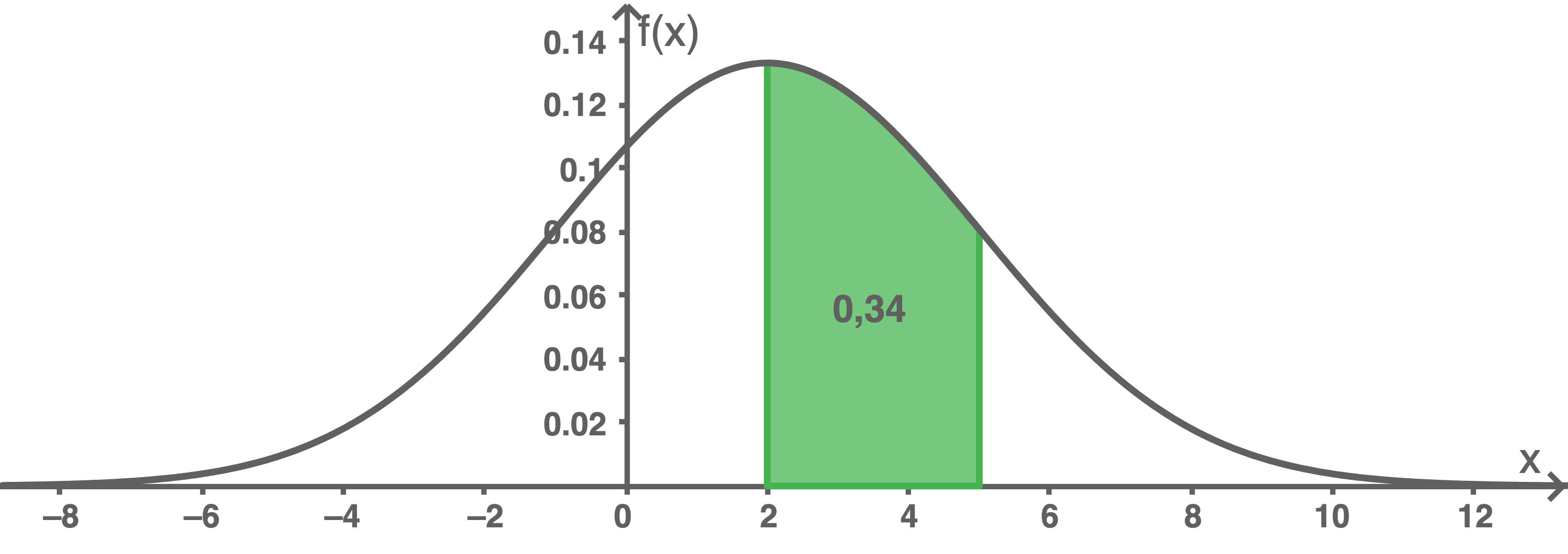

a)
Gib den Erwartungswert der Zufallsgröße  an.
an.
(1 BE)
b)
Bestimme mit Hilfe der graphischen Darstellung die folgenden Wahrscheinlichkeiten:
(4 BE)
1
2
a)
Die Tangente  berührt den Graphen
berührt den Graphen  an der Stelle
an der Stelle  ihre Steigung
ihre Steigung  beträgt somit
beträgt somit  Ableiten von
Ableiten von  liefert:
liefert:
 Für die Steigung der Tangente ergibt sich somit:
Für die Steigung der Tangente ergibt sich somit:
![\(\begin{array}[t]{rll}
m_t&=&f](https://mathjax.schullv.de/f09a6d8f4fb48ad9bce34590be4e3944bee6b41dd505348a5809aa111faddf24?color=5a5a5a)
b)
Die Tangente im Punkt  besitzt Steigung
besitzt Steigung  und berührt den Graphen
und berührt den Graphen  in diesem.
in diesem.
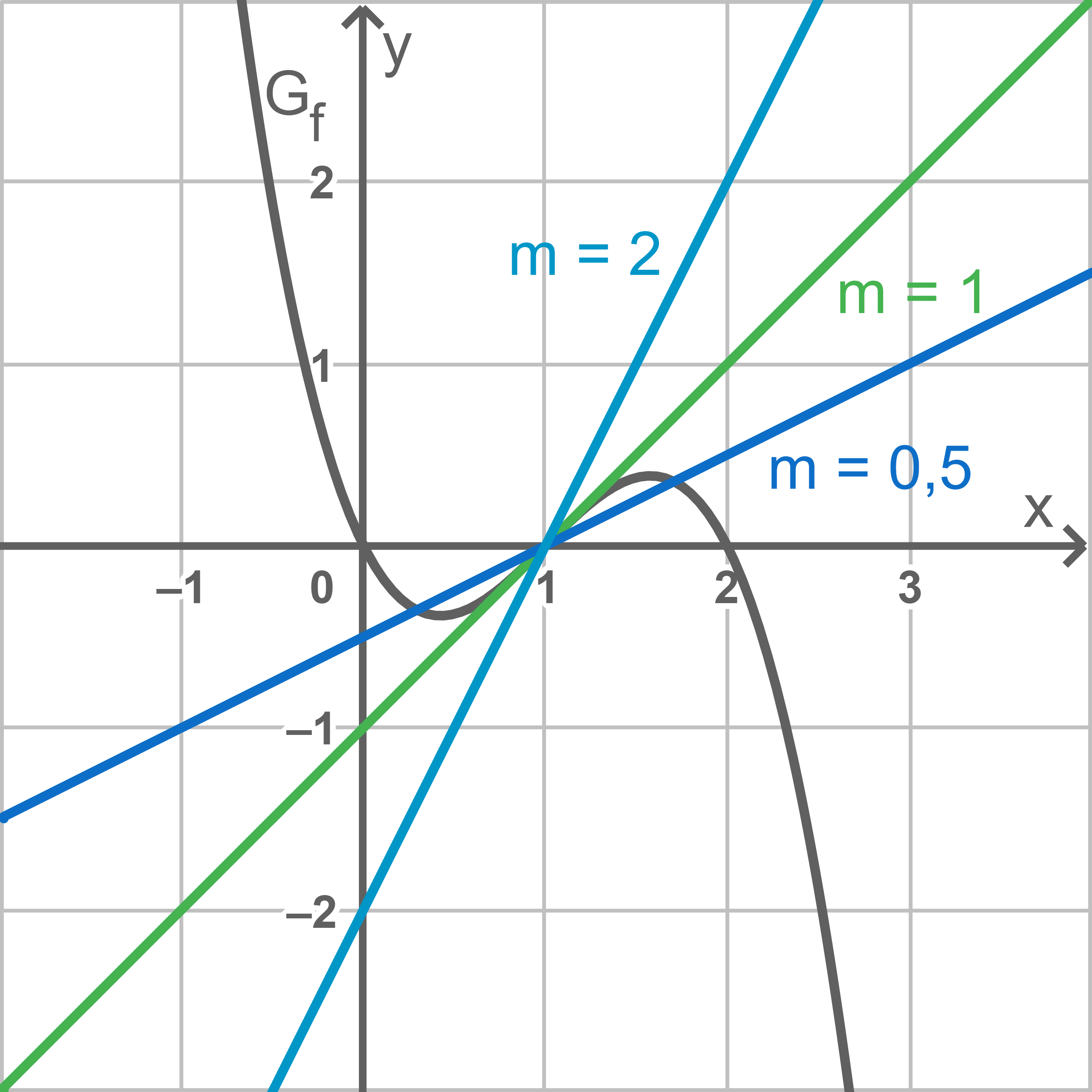 Die Skizze verdeutlicht, dass jede Gerade, die steiler verläuft, also eine Steigung
Die Skizze verdeutlicht, dass jede Gerade, die steiler verläuft, also eine Steigung  besitzt, den Graphen
besitzt, den Graphen  ebenfalls nur in einem Punkt schneidet, während jede Gerade die eine Steigung von
ebenfalls nur in einem Punkt schneidet, während jede Gerade die eine Steigung von  besitzt, den Graphen
besitzt, den Graphen  in drei Punkten schneidet.
in drei Punkten schneidet.

3
a)
b)
Einsetzen der Grenzen  und
und  ergibt:
Im Schnitt fließen in den ersten 10 Stunden somit 16,67 Liter Wasser pro Stunde aus dem Tank.
ergibt:
Im Schnitt fließen in den ersten 10 Stunden somit 16,67 Liter Wasser pro Stunde aus dem Tank.
4
a)
Der Graph  ist achsensymmetrisch, das heißt die Gerade
ist achsensymmetrisch, das heißt die Gerade  die parallel zur
die parallel zur  -Achse durch den Punkt
-Achse durch den Punkt  verläuft, schneidet den Graphen
verläuft, schneidet den Graphen  in den Punkten
in den Punkten  und
und  .
.
Damit der Abstand der beiden Punkte beträgt, muss
beträgt, muss  gelten, das heißt
gelten, das heißt  und somit
und somit  Für den Wert von
Für den Wert von  folgt nun:
folgt nun:

Damit der Abstand der beiden Punkte
b)
Das Dreieck ist gleichschenklig, wenn die Nullstelle der Tangente den gleichen Wert wie ihr  -Achsenabschnitt besitzt:
-Achsenabschnitt besitzt:
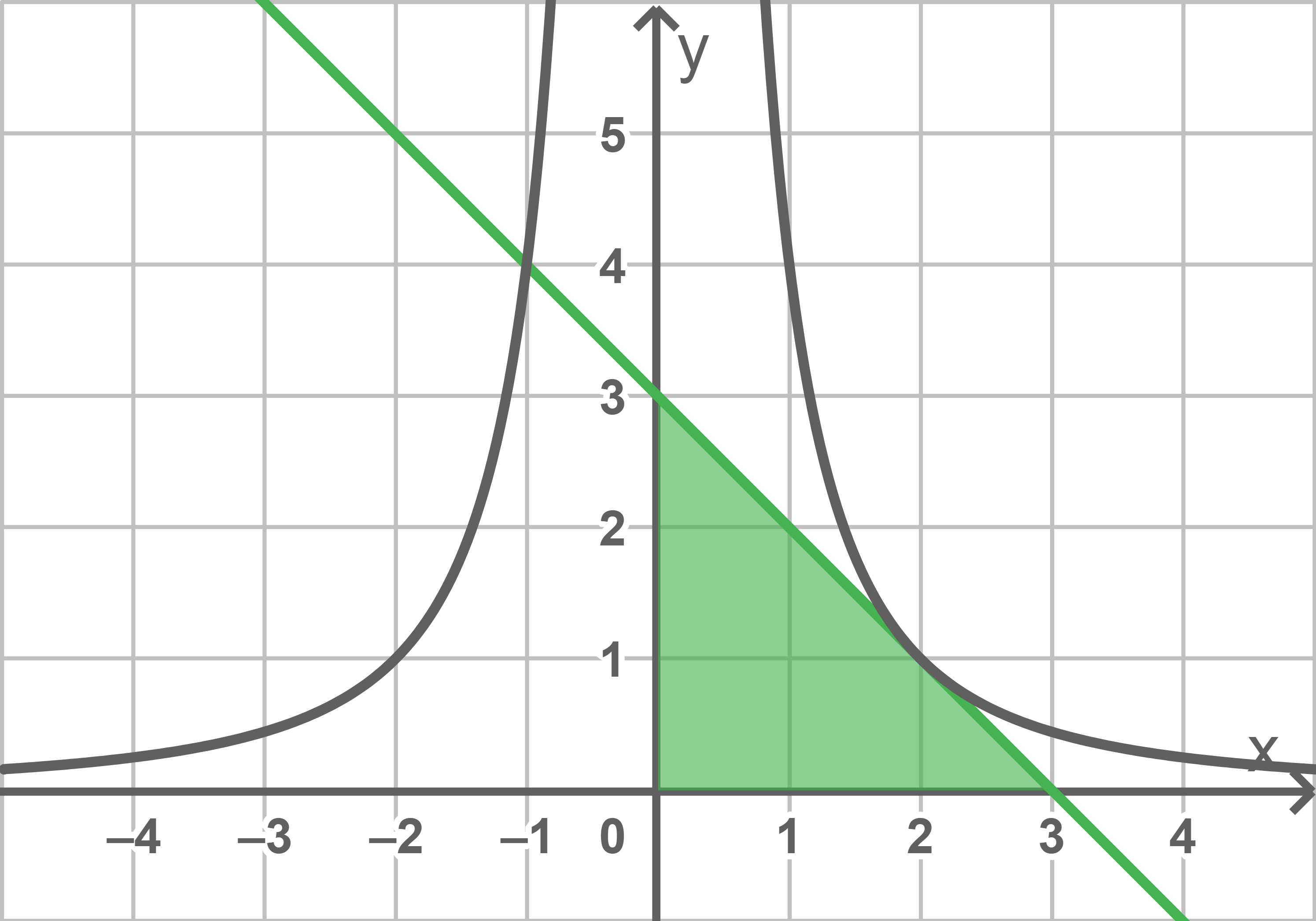 Eine solche Gerade hat die Steigung
Eine solche Gerade hat die Steigung  das heißt der Graph
das heißt der Graph  besitzt im Berührpunkt
besitzt im Berührpunkt  auch die Steigung
auch die Steigung  . Ableiten von
. Ableiten von 

 liefert:
liefert:
 Damit folgt für
Damit folgt für 
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/5a21e064e32acda220d9fc5140a89a93d0b486804503b5bf75583aabef358679?color=5a5a5a) Mit
Mit  ergeben sich die Koordinaten von
ergeben sich die Koordinaten von  somit als
somit als  .
.

5
a)
Die gesuchten Punkte sind jeweils in blauer Farbe verdeutlicht:

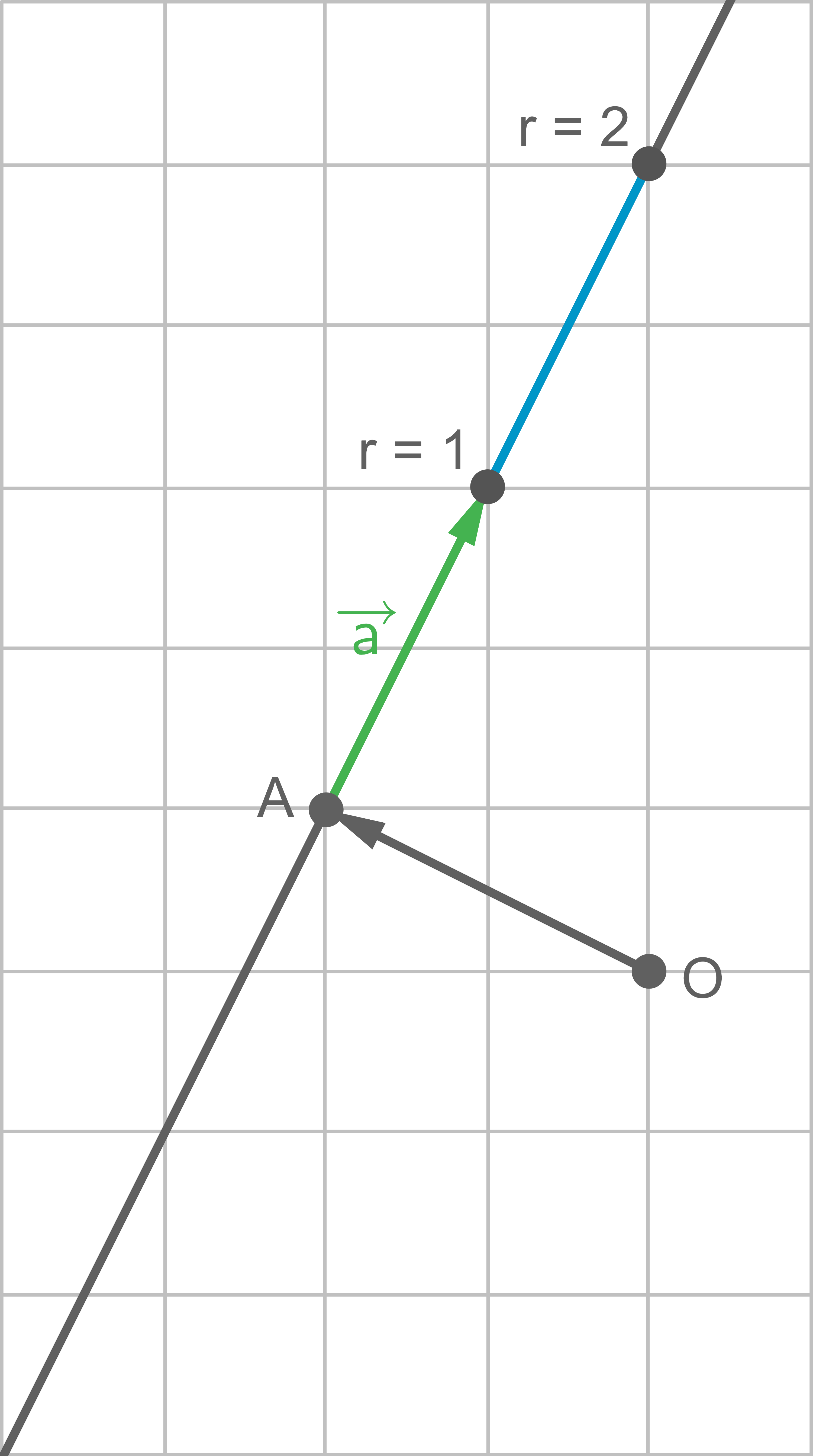

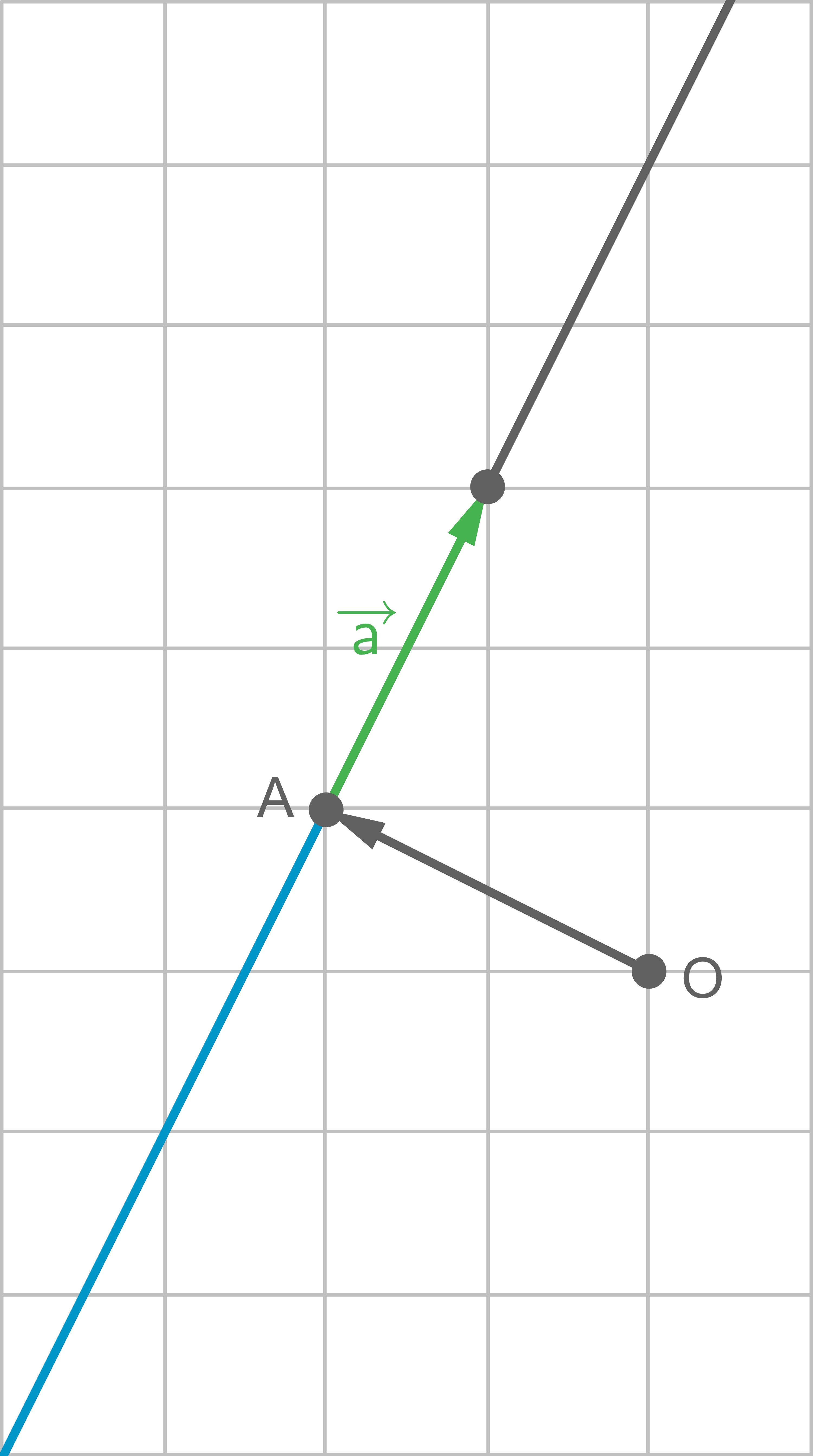

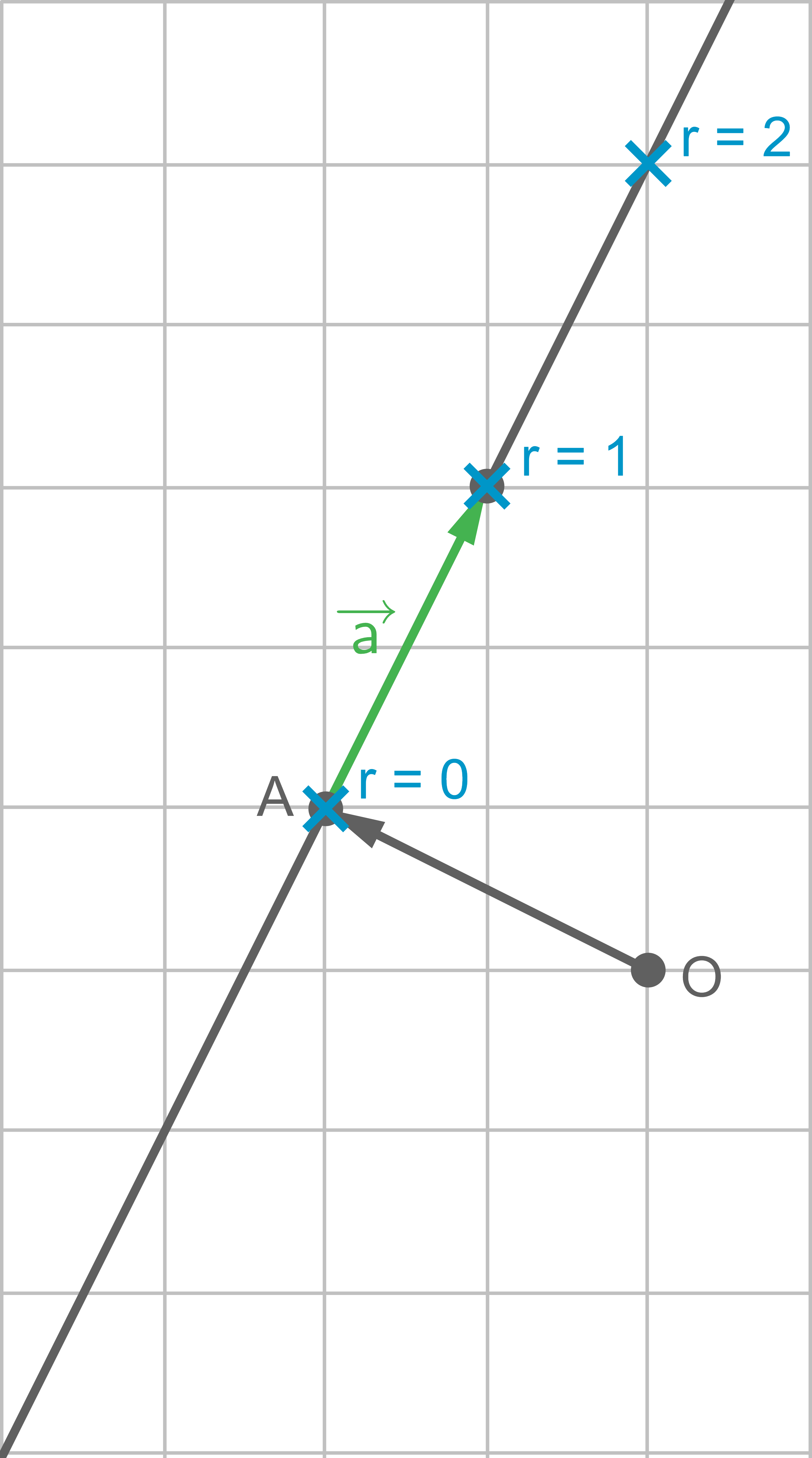



b)
Der Wert  liefert den Punkt
liefert den Punkt  Damit
Damit  die Strecke
die Strecke  im Verhältnis 1:3 teilt, muss der zugehörige Wert von
im Verhältnis 1:3 teilt, muss der zugehörige Wert von  also
also 


 betragen.
betragen.
c)
Da zu  der Wert
der Wert  gehört, ergibt sich für
gehört, ergibt sich für  der Wert von
der Wert von  als der negative Wert des Parameterwertes von
als der negative Wert des Parameterwertes von  Somit folgt, dass der zu
Somit folgt, dass der zu  gehörende Wert des Parameters
gehörende Wert des Parameters  beträgt.
beträgt.
6
a)
Der Richtungsvektor der Geraden  ist ein Richtungsvektor der
ist ein Richtungsvektor der  -Achse, d.h. die Gerade
-Achse, d.h. die Gerade  verläuft parallel zur
verläuft parallel zur  -Achse und damit orthogonal zur
-Achse und damit orthogonal zur  -Ebene. Somit liegt das Quadrat in der
-Ebene. Somit liegt das Quadrat in der  -Ebene.
-Ebene.
b)
Die Diagonalen des Quadrats schneiden sich im rechten Winkel in einem Punkt  Der Punkt
Der Punkt  ist dann ein dem Punkt
ist dann ein dem Punkt  benachbarter Eckpunkt des Quadrats, wenn die Punkte
benachbarter Eckpunkt des Quadrats, wenn die Punkte  und
und  ein gleichschenkliges und rechtwinkliges Dreieck bilden.
1. Schritt: Koordinaten von
ein gleichschenkliges und rechtwinkliges Dreieck bilden.
1. Schritt: Koordinaten von  berechnen
Da das Quadrat nach Aufgabenteil a) in der
berechnen
Da das Quadrat nach Aufgabenteil a) in der  -Ebene liegt, ist
-Ebene liegt, ist  der Punkt, in dem die Gerade
der Punkt, in dem die Gerade  die
die  -Ebene durchstößt. Gleichsetzen der
-Ebene durchstößt. Gleichsetzen der  -Koordinate eines allgemeinen Punktes auf
-Koordinate eines allgemeinen Punktes auf  mit Null liefert:
mit Null liefert:
![\(\begin{array}[t]{rll}
5+t\cdot 1&=&0& \quad \scriptsize \mid\; -5 \\[5pt]
t&=&-5
\end{array}\)](https://mathjax.schullv.de/72db794e84b739641d718c153435b2331a23c5e7f55bd99bcb6efec2aa8beab7?color=5a5a5a) Einsetzen von
Einsetzen von  in in die Geradengleichung von
in in die Geradengleichung von  ergibt für die Koordinaten des Schnittpunkts
ergibt für die Koordinaten des Schnittpunkts  der Diagonalen
der Diagonalen  2. Schritt: Eigenschaften von
2. Schritt: Eigenschaften von  nachweisen
Da
nachweisen
Da  gilt, ist das Dreieck
gilt, ist das Dreieck  gleichschenklig. Zudem folgt:
Somit stehen die beiden Schenkel des Dreiecks
gleichschenklig. Zudem folgt:
Somit stehen die beiden Schenkel des Dreiecks  orthogonal aufeinander, das heißt sie schließen einen rechten Winkel ein. Damit ist das Dreieck gleichschenklig und rechtwinklig, der Punkt
orthogonal aufeinander, das heißt sie schließen einen rechten Winkel ein. Damit ist das Dreieck gleichschenklig und rechtwinklig, der Punkt  ist also einer der Eckpunkte des Quadrats, die dem Punkt
ist also einer der Eckpunkte des Quadrats, die dem Punkt  benachbart sind.
benachbart sind.
7
a)
Das Diagramm in Abbildung 8 kann die Wahrscheinlichkeitsverteilung von  nicht darstellen, da die Zufallsvariable keine Werte
nicht darstellen, da die Zufallsvariable keine Werte  annimmt, und somit auch deren Wahrscheinlichkeit nicht größer als Null sein kann.
annimmt, und somit auch deren Wahrscheinlichkeit nicht größer als Null sein kann.
Das Diagramm in Abbildung 10 stellt die Wahrscheinlichkeitsverteilung von ebenfalls nicht dar, da die Summe aller Wahrscheinlichkeiten genau
ebenfalls nicht dar, da die Summe aller Wahrscheinlichkeiten genau  ergeben muss, die Werte für
ergeben muss, die Werte für  und
und  allerdings addiert schon größer als
allerdings addiert schon größer als  sind.
sind.
Das Diagramm in Abbildung 10 stellt die Wahrscheinlichkeitsverteilung von
b)
Die mit den Parametern  und
und  binomialverteilte Zufallsgröße
binomialverteilte Zufallsgröße  ist symmetrisch, woraus direkt
ist symmetrisch, woraus direkt  folgt. Einsetzen in die Formel
folgt. Einsetzen in die Formel  des Erwartungswerts liefert:
des Erwartungswerts liefert:
![\(\begin{array}[t]{rll}
8&=&n\cdot 0,5&\quad \scriptsize \mid\; \cdot2\\[5pt]
16&=&n
\end{array}\)](https://mathjax.schullv.de/aa9f2438b6a0f3a06f77a14f054edd773dbfa8653b89036b95f3cd0bd8562db6?color=5a5a5a)
8
a)
Der Erwartungswert einer normalverteilten Zufallsgröße ist die Extremstelle seiner Dichtefunktion. Aus der Abbildung folgt somit 
b)