Teil C1
1
Ein Logistikunternehmen testet auf einer Strecke zwischen Festland und einer Insel die Paketzustellung mithilfe eines Flugkörpers, einer sogenannten Drohne. In einem kartesischen Koordinatensystem wird das horizontale Gelände, über dem sich die Drohne bewegt, modellhaft durch die  -Ebene dargestellt, die Lage des Startplatzes durch den Punkt
-Ebene dargestellt, die Lage des Startplatzes durch den Punkt  und die Lage des regulären Landeplatzes durch den Punkt
und die Lage des regulären Landeplatzes durch den Punkt  .
.
Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Realität.
Die Drohne soll über dem Startplatz zunächst vertikal aufsteigen, bis sie eine Höhe von erreicht hat, und anschließend geradlinig in konstanter Höhe und mit konstanter Geschwindigkeit in die Richtung des Landeplatzes fliegen.
erreicht hat, und anschließend geradlinig in konstanter Höhe und mit konstanter Geschwindigkeit in die Richtung des Landeplatzes fliegen.
Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Realität.
Die Drohne soll über dem Startplatz zunächst vertikal aufsteigen, bis sie eine Höhe von
a)
Begründe, dass die vorgesehene horizontale Flugbahn der Drohne im Modell entlang der Gerade

 mit
mit  verläuft.
verläuft.
(2 BE)
b)
Zeige, dass sich die Drohne auf der vorgesehenen Flugbahn befindet. Bestimme die Koordinaten des Punkts, der die Position der Drohne nach weiteren  Sekunden Flugzeit auf der vorgesehenen Flugbahn darstellt.
Sekunden Flugzeit auf der vorgesehenen Flugbahn darstellt.
(3 BE)
c)
Bestimme die Geschwindigkeit der Drohne während des horizontalen Flugs.
(2 BE)
Die Drohne soll ihren Weg zum Landeplatz selbständig zurücklegen können. Während der Testphase wird ihr Flug von einer Bodenstation aus überwacht und die Flugbahn bei Bedarf korrigiert. Die Position der Bodenstation wird durch den Punkt  dargestellt, ihre Reichweite beträgt
dargestellt, ihre Reichweite beträgt 
d)
Weise nach, dass sich die Drohne auf dem horizontalen Teil der vorgesehenen Flugbahn über eine Strecke von mehr als  innerhalb der Reichweite der Bodenstation befindet.
innerhalb der Reichweite der Bodenstation befindet.
(5 BE)
Einer Korrektur der Bodenstation folgend, weicht die Drohne im Modell im Punkt  von der vorgesehenen Flugbahn ab und bewegt sich mit einer Geschwindigkeit von
von der vorgesehenen Flugbahn ab und bewegt sich mit einer Geschwindigkeit von  geradlinig auf einen Ausweichlandplatz zu, der durch den Punkt
geradlinig auf einen Ausweichlandplatz zu, der durch den Punkt  dargestellt wird.
dargestellt wird.
e)
Bestimme die Größe des Neigungswinkels der Flugbahn gegenüber dem Gelände beim Anflug auf den Ausweichlandeplatz.
(3 BE)
f)
Berechne, um wie viele Meter sich die Flughöhe pro Sekunde verringert.
(3 BE)
Nach der Landung auf dem Ausweichplatz steuert die Drohne eine Position an, die sich in einer Höhe von  befindet und vom Startplatz, vom regulären Landeplatz und der Bodenstation gleich weit entfernt ist. Diese Position wird durch den Punkt
befindet und vom Startplatz, vom regulären Landeplatz und der Bodenstation gleich weit entfernt ist. Diese Position wird durch den Punkt  beschrieben.
beschrieben.
g)
Die Ebene  enthält alle Punkt, die von
enthält alle Punkt, die von  und
und  den gleichen Abstand haben.
den gleichen Abstand haben.
Bestimme eine Gleichung von in Koordinatenform.
in Koordinatenform.
Bestimme eine Gleichung von
(3 BE)
h)
Übernimm die Darstellung und stelle die Ebene  dar.
dar.
Beschreibe ein Verfahren, mit dem unter Verwendung der Abbildung die Koordinaten von ermittelt werden könnten.
ermittelt werden könnten.
Veranschauliche das Verfahren in deiner Darstellung.
Beschreibe ein Verfahren, mit dem unter Verwendung der Abbildung die Koordinaten von
Veranschauliche das Verfahren in deiner Darstellung.
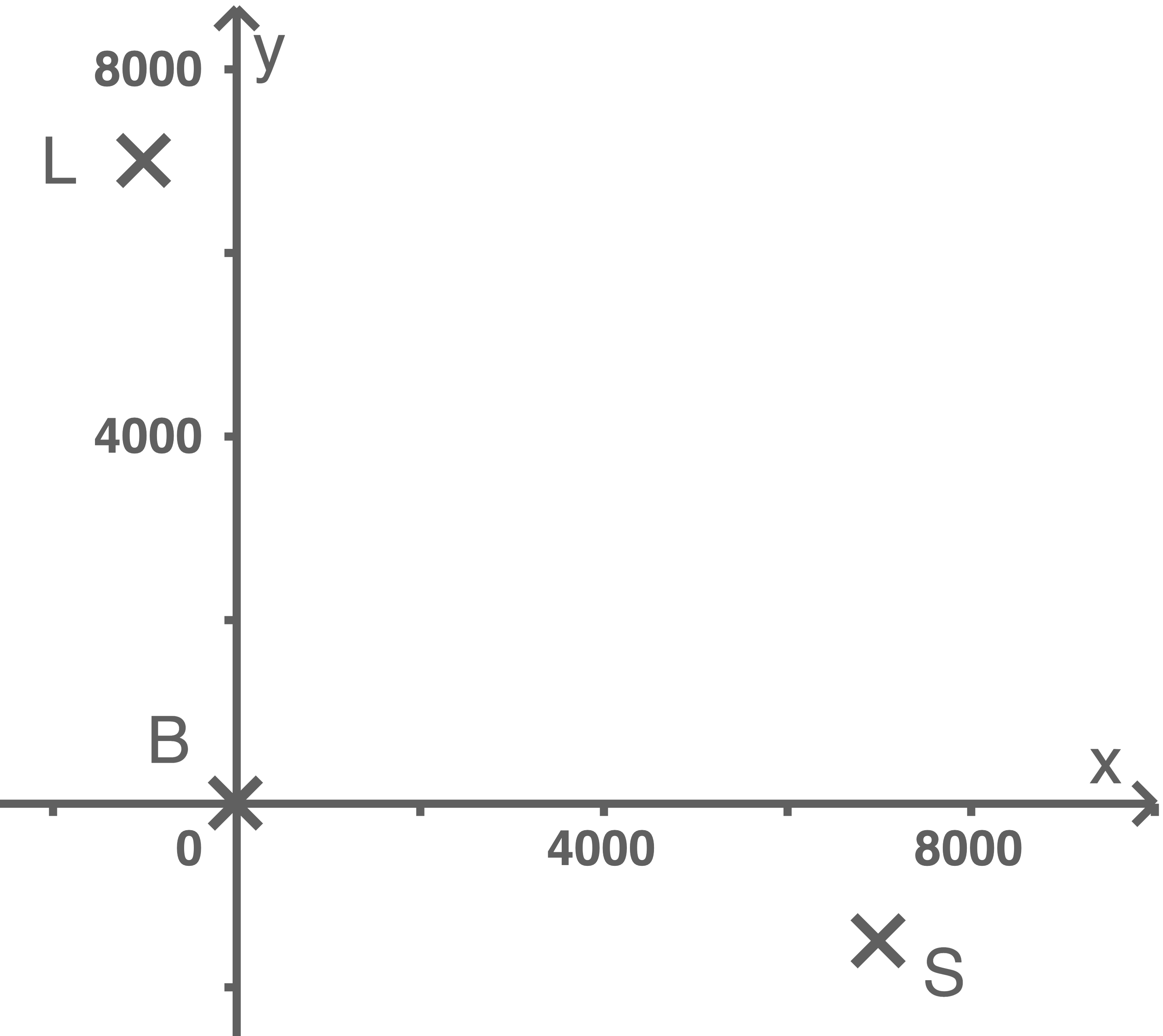
(4 BE)
2
An einem Kiosk kann man Rubbellose kaufen. Ein Los besteht aus insgesamt  Feldern. Auf jedem Feld steht genau eine Zahl. Auf acht Feldern steht
Feldern. Auf jedem Feld steht genau eine Zahl. Auf acht Feldern steht  , auf vier Feldern
, auf vier Feldern  und auf den restlichen vier Feldern steht die Zahl
und auf den restlichen vier Feldern steht die Zahl  . Die Zahlen sind zufällig auf die Felder verteilt und werden erst nach dem Freirubbeln sichtbar. Der Käufer eines Loses darf genau zwei Felder freirubbeln (siehe Abbildung). Der Auszahlungsbetrag in Euro ergibt sich aus dem Produkt der beiden sichtbaren Zahlen.
. Die Zahlen sind zufällig auf die Felder verteilt und werden erst nach dem Freirubbeln sichtbar. Der Käufer eines Loses darf genau zwei Felder freirubbeln (siehe Abbildung). Der Auszahlungsbetrag in Euro ergibt sich aus dem Produkt der beiden sichtbaren Zahlen.
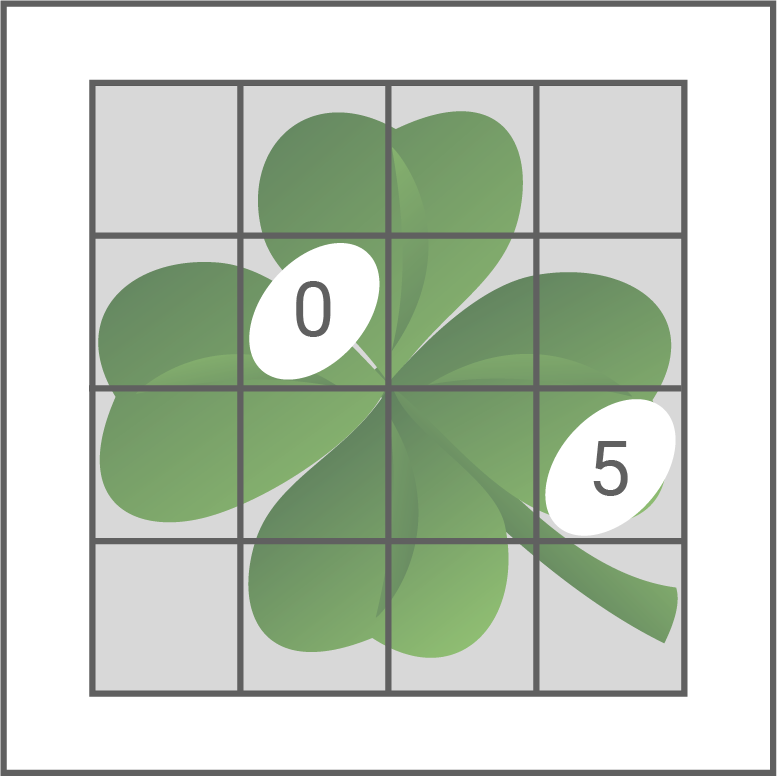
a)
Eine Frau kauft ein Rubellos und rubbelt genau zwei Felder frei.
Ermittle die Wahrscheinlichkeiten folgender Ereignisse:
 = „Die Frau rubbelt zuerst ein Feld frei, das keine
= „Die Frau rubbelt zuerst ein Feld frei, das keine  anzeigt.“
anzeigt.“
 = „Der Frau werden
= „Der Frau werden  ausgezahlt.“
ausgezahlt.“
Ermittle die Wahrscheinlichkeiten folgender Ereignisse:
(2 BE)
b)
Ein Mann kauft  Lose.
Lose.
Berechne die Wahrscheinlichkeiten folgender Ereignisse:
 = „Der Mann erhält genau einmal
= „Der Mann erhält genau einmal  .“
.“
 = „Der Mann erhält mindestens fünfmal
= „Der Mann erhält mindestens fünfmal  .“
.“
Berechne die Wahrscheinlichkeiten folgender Ereignisse:
(4 BE)
c)
Weise nach, dass die Wahrscheinlichkeit, mit der ein Kunde beim Kauf eines Rubbelloses mindestens einen Betrag von  ausgezahlt bekommt,
ausgezahlt bekommt,  beträgt.
beträgt.
Bestimme die Anzahl der Lose, die er mindestens kaufen muss, um mit einer Wahrscheinlichkeit von mindestens mindestens einmal einen Betrag von mindestens
mindestens einmal einen Betrag von mindestens  ausgezahlt zu bekommen.
ausgezahlt zu bekommen.
Bestimme die Anzahl der Lose, die er mindestens kaufen muss, um mit einer Wahrscheinlichkeit von mindestens
(5 BE)
d)
Der Kioskbesitzer behauptet, dass  seiner Kunden Loskäufer sind. Ein Schüler, der als Aushilfe im Kiosk arbeitet, bezweifelt die Aussage des Kioskbesitzers. Mithilfe eines zweiseitigen Signifikanztest vom Umfang
seiner Kunden Loskäufer sind. Ein Schüler, der als Aushilfe im Kiosk arbeitet, bezweifelt die Aussage des Kioskbesitzers. Mithilfe eines zweiseitigen Signifikanztest vom Umfang  und einem Signifikanzniveau von
und einem Signifikanzniveau von  will er die Hypothese
will er die Hypothese  testen.
testen.
Ermittle den Verwerfungsbereich des Tests.
Unter den nächsten Kunden zählt er
Kunden zählt er  Losverkäufer.
Losverkäufer.
Beurteile anhand deines Ergebnisses die Zweifel des Schülers.
Ermittle den Verwerfungsbereich des Tests.
Unter den nächsten
Beurteile anhand deines Ergebnisses die Zweifel des Schülers.
(4 BE)
1
a)
Da die Drohne zunächst  vertikal aufsteigt bevor sie losfliegt, muss die
vertikal aufsteigt bevor sie losfliegt, muss die  -Koordinate des Stützvektors der Flugbahn um
-Koordinate des Stützvektors der Flugbahn um  größer als die des Startpunkts
größer als die des Startpunkts  sein. Da die Drohne in konstanter Höhe fliegt, muss zudem die
sein. Da die Drohne in konstanter Höhe fliegt, muss zudem die  -Koordinate des Richtungsvektors Null sein. Für die Flugrichtung der Drohne ergibt sich somit der Vektor
-Koordinate des Richtungsvektors Null sein. Für die Flugrichtung der Drohne ergibt sich somit der Vektor  mit
mit  -Koordinate
-Koordinate 
 Zusammen mit den oben begründeten Koordinaten
Zusammen mit den oben begründeten Koordinaten  des Stützvektors folgt für die Gleichung der Geraden, die die Flugbahn beschreibt:
des Stützvektors folgt für die Gleichung der Geraden, die die Flugbahn beschreibt:


b)
Position der Drohne auf der Flugbahn zeigen
Daraus ergibt sich folgendes Gleichungssystem:
 Lösen des Gleichungssystems mit dem CAS liefert:
Lösen des Gleichungssystems mit dem CAS liefert:
 Der Punkt
Der Punkt  liegt somit auf der Geraden
liegt somit auf der Geraden  das heißt die Drohne befindet sich auf der vorgesehenen Flugbahn.
Koordinaten der neuen Position bestimmen
Da die Drohe mit konstanter Geschwindigkeit fliegt und sich
das heißt die Drohne befindet sich auf der vorgesehenen Flugbahn.
Koordinaten der neuen Position bestimmen
Da die Drohe mit konstanter Geschwindigkeit fliegt und sich  Sekunden nachdem Start auf der Position
Sekunden nachdem Start auf der Position  die durch einsetzen von
die durch einsetzen von  in die Gerade
in die Gerade  erhalten wird, befindet, liefert Einsetzen von
erhalten wird, befindet, liefert Einsetzen von  für die Position der Drohne nach weiteren
für die Position der Drohne nach weiteren  Sekunden:
Sekunden:


 Nach weiteren
Nach weiteren  Sekunden Flugzeit wird die Position der Drohne somit durch den Punkt mit den Koordinaten
Sekunden Flugzeit wird die Position der Drohne somit durch den Punkt mit den Koordinaten  beschrieben.
beschrieben.
c)
Die Strecke, die die Drohne in  Sekunden zurücklegt, wird zum Beispiel durch die Länge des Vektors
Sekunden zurücklegt, wird zum Beispiel durch die Länge des Vektors  beschrieben. Mit dem norm-Befehl des CAS folgt:
beschrieben. Mit dem norm-Befehl des CAS folgt:
![\(\left\vert\overrightarrow{S_1P} \right\vert \approx 1206,00\;[\text{m}]\)](https://mathjax.schullv.de/9b74d36347b2a7fad59f71a3dca87c30bbea7302eba5914568b0fb301fa7918a?color=5a5a5a) Somit bewegt sich die Drohe während des horizontalen Flugs mit einer Geschwindigkeit von ca.
Somit bewegt sich die Drohe während des horizontalen Flugs mit einer Geschwindigkeit von ca. 
![\( = 12\;\left[\frac{\text{m}}{\text{s}}\right].\)](https://mathjax.schullv.de/008dc2e9a0046a98706100ac59e0d01f086ff852a65e7e361d49f5f411d4c41f?color=5a5a5a)
d)
Während des horizontalen Fluges wird die Position der Drohne durch die Punkte der Geraden  beschrieben. Diese Punkte haben die folgende allgemeine Form:
beschrieben. Diese Punkte haben die folgende allgemeine Form:
 Gesucht ist nun der Bereich, in dem sich
Gesucht ist nun der Bereich, in dem sich  befinden kann, sodass der Punkt von
befinden kann, sodass der Punkt von  einen Abstand von höchstens
einen Abstand von höchstens  besitzt, das heißt
besitzt, das heißt  gilt. Mit Hilfe des solve-Befehls des CAS folgt für
gilt. Mit Hilfe des solve-Befehls des CAS folgt für 
 Einsetzen der Grenzwerte
Einsetzen der Grenzwerte  und
und  liefert die Positionen mit den Koordinaten
liefert die Positionen mit den Koordinaten  und
und  Für die Länge der Strecke zwischen diesen beiden Positionen folgt mit dem CAS:
Für die Länge der Strecke zwischen diesen beiden Positionen folgt mit dem CAS:
![\(\begin{array}[t]{rll}
\left\vert\overrightarrow{P_2P_3} \right\vert&=& \left\vert\pmatrix{-6038,046 \\ 6350,484 \\ 0} \right\vert \\[5pt]
&\approx& 8763 \; [\text{m}]
\end{array}\)](https://mathjax.schullv.de/34ee052debdada33bfe3930bf3e32ee06f8247f55df74419df7fc944feb9b08e?color=5a5a5a) Auf einer Strecke von ca.
Auf einer Strecke von ca.  das heißt mehr als
das heißt mehr als  befindet sich die Drohne in Reichweite der Bodenstation.
befindet sich die Drohne in Reichweite der Bodenstation.
e)
Die abgeänderte Flugbahn wird durch die Gerade mit der folgenden Gleichung beschrieben:
![\(\begin{array}[t]{rll}
h:\overrightarrow{x} &=& \overrightarrow{OQ} + r\cdot \overrightarrow{QA} \\[5pt]
&=& \pmatrix{3996\\ 1746 \\ 50} + s\cdot \pmatrix{54 \\ 64 \\ -50}
\end{array}\)](https://mathjax.schullv.de/071dc8941e9a553c21c03ed9f2c395be76a7de7f1f2020e73a646bbf5da597bb?color=5a5a5a) Der Neigungswinkel der abgeänderten Flugbahn gegenüber dem Gelände entspricht dem Schnittwinkel der Geraden
Der Neigungswinkel der abgeänderten Flugbahn gegenüber dem Gelände entspricht dem Schnittwinkel der Geraden  mit der
mit der  -Ebene.
-Ebene.
Ein Normalenvektor dieser Ebene ist
Somit folgt: Der Neigungswinkel der abgeänderten Flugbahn gegenüber dem Gelände beträgt ca.
Ein Normalenvektor dieser Ebene ist
Somit folgt: Der Neigungswinkel der abgeänderten Flugbahn gegenüber dem Gelände beträgt ca.
f)
Vom Punkt  zum Punkt
zum Punkt  verringert die Drohne ihre Höhe um
verringert die Drohne ihre Höhe um  Dabei legt die Drohne folgende Strecke zurück:
Dabei legt die Drohne folgende Strecke zurück:
![\(\begin{array}[t]{rll}
\left|\overrightarrow{QA} \right|&=& \left| \pmatrix{54\\64 \\-50} \right| \\[5pt]
&=& \sqrt{9512}
\end{array}\)](https://mathjax.schullv.de/b73d32e7a0b0798a3414138f2ec03fd59845163fa256a78112f6c24bad458d83?color=5a5a5a) Mit Hilfe der Geschwindigkeit der Drohne von
Mit Hilfe der Geschwindigkeit der Drohne von  folgt für die Zeit die sie dafür benötigt:
folgt für die Zeit die sie dafür benötigt:
 Die Verringerung der Höhe pro Sekunde ergibt sich somit wie folgt:
Die Verringerung der Höhe pro Sekunde ergibt sich somit wie folgt:
![\(\dfrac{50}{\frac{\sqrt{9512}}{5}} \approx 2,56\;\left[\dfrac{\text{m}}{\text{s}}\right] \)](https://mathjax.schullv.de/9890f5e55bc5cf2ee3483b89ce36c84f11676d67a605b5aca1afff55cfd523a5?color=5a5a5a) Pro Sekunde verringert sich die Flughöhe der Drohne somit um ca.
Pro Sekunde verringert sich die Flughöhe der Drohne somit um ca. 
g)
Die Ebene  muss senkrecht zur Strecke
muss senkrecht zur Strecke  verlaufen und deren Mittelpunkt enthalten, damit alle Punkte mit gleichem Abstand zu
verlaufen und deren Mittelpunkt enthalten, damit alle Punkte mit gleichem Abstand zu  und
und  enthalten sind. Ein möglicher Normalenvektor von
enthalten sind. Ein möglicher Normalenvektor von  ist somit:
ist somit:
 Für die Koordinaten des Mittelpunkts der Strecke
Für die Koordinaten des Mittelpunkts der Strecke  folgt:
Einsetzen der Koordinaten von
folgt:
Einsetzen der Koordinaten von  in
in  liefert für
liefert für 

 Eine Gleichung von
Eine Gleichung von  in Koordinatenform lautet somit:
in Koordinatenform lautet somit:


h)
Ebene darstellen
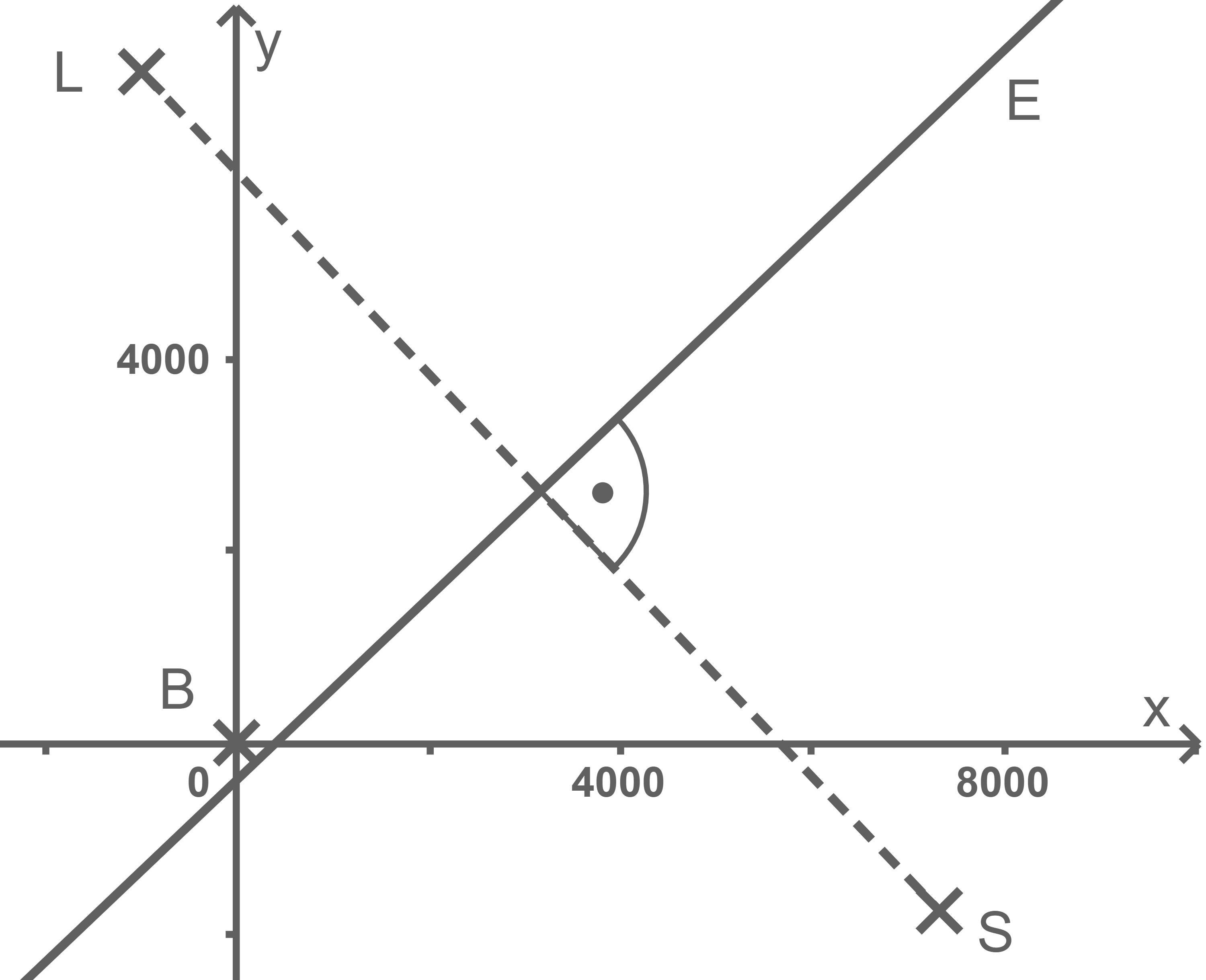 Verfahren beschreiben
Analog zur Ebene
Verfahren beschreiben
Analog zur Ebene  gibt es eine Ebene
gibt es eine Ebene  in der alle Punkte liegen, die von
in der alle Punkte liegen, die von  und
und  gleichweit entfernt sind. Diese Ebene kann in der Abbildung ebenfalls durch eine Gerade dargestellt werden, die analog zum Vorgehen bei
gleichweit entfernt sind. Diese Ebene kann in der Abbildung ebenfalls durch eine Gerade dargestellt werden, die analog zum Vorgehen bei  die Mittelsenkrechte der Strecke
die Mittelsenkrechte der Strecke  ist.
ist.
Die beiden Ebenen schneiden sich in einer Gerade, auf der dann alle Punkte liegen, welche gleichweit von und
und  entfernt sind. Da diese senkrecht zur
entfernt sind. Da diese senkrecht zur  -Ebene steht, wird sie in der Abbildung durch einen Punkt
-Ebene steht, wird sie in der Abbildung durch einen Punkt  dargestellt.
dargestellt.
Der Punkt liegt auf dieser Geraden, besitzt also die gleichen
liegt auf dieser Geraden, besitzt also die gleichen  - und
- und  -Koordinaten wie
-Koordinaten wie  und seine
und seine  -Koordinate beträgt
-Koordinate beträgt  Verfahren veranschaulichen
Verfahren veranschaulichen
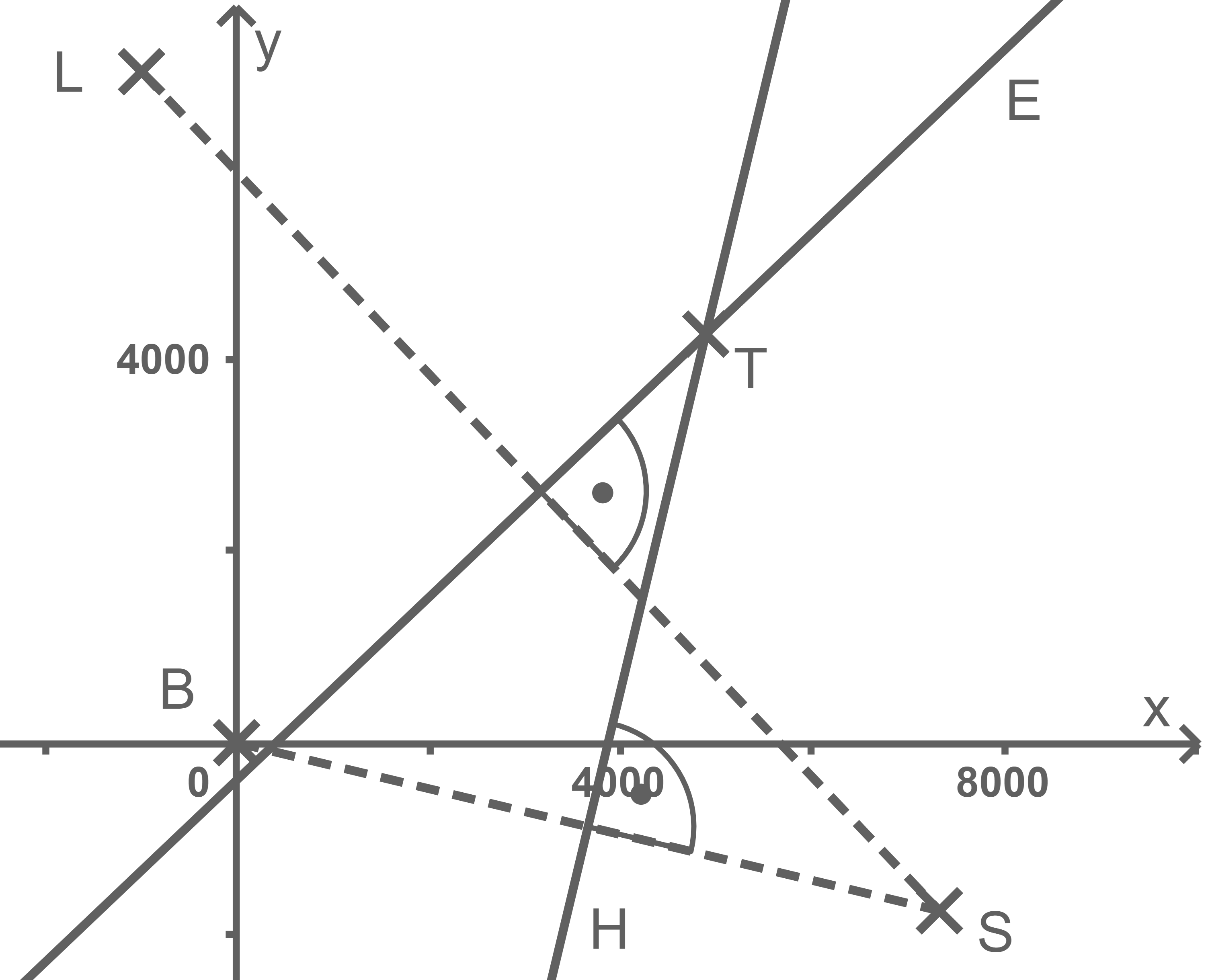

Die beiden Ebenen schneiden sich in einer Gerade, auf der dann alle Punkte liegen, welche gleichweit von
Der Punkt

2
a)
b)
Die Zufallsvariable  beschreibt wie oft der Mann
beschreibt wie oft der Mann  ausgezahlt bekommt und ist binomialverteilt mit den Parametern
ausgezahlt bekommt und ist binomialverteilt mit den Parametern  und
und  Mit dem CAS folgt:
Mit dem CAS folgt:






c)
Wahrscheinlichkeit nachweisen
Eine Auszahlung von mindestens  kommt genau dann zustande, wenn entweder eine
kommt genau dann zustande, wenn entweder eine  und eine
und eine  in beliebiger Reihenfolge, oder eine
in beliebiger Reihenfolge, oder eine  und eine
und eine  freigerubbelt werden. Mit den Pfadregeln folgt:
freigerubbelt werden. Mit den Pfadregeln folgt:




 Anzahl der Lose bestimmen
Die Zufallsgröße
Anzahl der Lose bestimmen
Die Zufallsgröße  beschreibt unter
beschreibt unter  Losen die Anzahl der Lose bei denen mehr als
Losen die Anzahl der Lose bei denen mehr als  ausgezahlt werden und ist binomialverteilt mit
ausgezahlt werden und ist binomialverteilt mit  und unbekanntem
und unbekanntem  Es folgt:
Mit dem solve-Befehl des CAS folgt für
Es folgt:
Mit dem solve-Befehl des CAS folgt für 
 Der Kunde muss somit mindestens
Der Kunde muss somit mindestens  Lose kaufen um mit einer Wahrscheinlichkeit von mindestens
Lose kaufen um mit einer Wahrscheinlichkeit von mindestens  mindestens einmal mindestens
mindestens einmal mindestens  ausgezahlt zu bekommen.
ausgezahlt zu bekommen.
d)
Verwerfungsbereich des Tests ermitteln
Der Verwerfungsbereich eines zweiseitiger Signifikanztest mit einer Stichprobe von  Kunden hat folgende Form:
Kunden hat folgende Form:
 Die Zufallsgröße
Die Zufallsgröße  gibt die die Anzahl der Kunden an, die ein Los kaufen und ist binomialverteilt mit
gibt die die Anzahl der Kunden an, die ein Los kaufen und ist binomialverteilt mit  und laut Nullhypothese
und laut Nullhypothese  Mit dem Signifikanzniveau
Mit dem Signifikanzniveau  folgt mit Hilfe des CAS durch systematisches Ausprobieren:
folgt mit Hilfe des CAS durch systematisches Ausprobieren:









 Somit folgt
Somit folgt  und
und  das heißt der Verwerfungsbereich lautet
das heißt der Verwerfungsbereich lautet  Zweifel des Schülers beurteilen
Die Anzahl der Loskäufer liegt nicht im Verwerfungsbereich
Zweifel des Schülers beurteilen
Die Anzahl der Loskäufer liegt nicht im Verwerfungsbereich  Die Nullhypothese, dass
Die Nullhypothese, dass  der Kunden Loskäufer sind, kann damit nicht widerlegt werden, das heißt die Zweifel des Schülers werden von dieser Stichprobe nicht untermauert.
der Kunden Loskäufer sind, kann damit nicht widerlegt werden, das heißt die Zweifel des Schülers werden von dieser Stichprobe nicht untermauert.