Teil C1
1
Gegeben sind die Punkte 
 und
und  .
.
 bilden die Punkte
bilden die Punkte 
 und
und  eine dreiseitige Pyramide
eine dreiseitige Pyramide 
a)
Weise nach, dass das Dreieck  ein gleichseitiges Dreieck ist.
ein gleichseitiges Dreieck ist.
(3 BE)
b)
Die Punkte 
 und
und  liegen in einer Ebene
liegen in einer Ebene  .
.
Beschreibe eine Vorgehensweise zur Ermittlung einer Koordinatengleichung von .
Ein Normalenvektor von
.
Ein Normalenvektor von  ist
ist  .
Gib eine Koordinatengleichung von
.
Gib eine Koordinatengleichung von  an.
an.
Beschreibe eine Vorgehensweise zur Ermittlung einer Koordinatengleichung von
(4 BE)
c)
Berechne die Größe des Neigungswinkels des Dreiecks  zur
zur  -Ebene.
-Ebene.
(3 BE)
d)
Auf der Geraden  mit
mit  gibt es einen Punkt
gibt es einen Punkt  , der vom Koordinatenursprung
, der vom Koordinatenursprung  und vom Punkt
und vom Punkt  den gleichen Abstand hat.
Berechne die Koordinate von
den gleichen Abstand hat.
Berechne die Koordinate von 
Gemeinsam mit dem Koordinatenursprung
(3 BE)
e)
Berechne das Volumen dieser Pyramide.
(3 BE)
f)
Stelle diese Pyramide in einem Koordinatensystem dar. Veranschauliche verdeckte Körperkanten.
Zeichne in die Darstellung die senkrechte Projektion der Pyramide in die -Ebene ein.
-Ebene ein.
Zeichne in die Darstellung die senkrechte Projektion der Pyramide in die
(4 BE)
g)
Eine Ebene  soll die Pyramide in zwei volumengleiche Teilkörper zerlegen.
Veranschauliche im Koordinatensystem aus Teilaufgabe 1 f) die Schnittfläche einer solchen Ebene mit der Pyramide.
Begründe, dass die von dir gewählte Ebene die Bedingung erfüllt.
soll die Pyramide in zwei volumengleiche Teilkörper zerlegen.
Veranschauliche im Koordinatensystem aus Teilaufgabe 1 f) die Schnittfläche einer solchen Ebene mit der Pyramide.
Begründe, dass die von dir gewählte Ebene die Bedingung erfüllt.
Gib eine Gleichung für an.
an.
Gib eine Gleichung für
(5 BE)
2
An einem Montag wurden die Schüler eines Gymnasiums befragt, auf welche Art sie die Schule erreichten:
Die relativen Häufigkeiten werden im Folgenden als Wahrscheinlichkeiten interpretiert.
Betrachtet werden folgende Ereignisse:
A: = „Unter 20 befragten Schülern kamen höchstens 5 mit dem Fahrrad.“
B: = „Von 100 befragten Schülern nutzten mindestens 20 den ÖPNV.“
C: = „Unter 80 befragten Schülern waren mindestens 20 und höchstens 30 Fußgänger.“
motorisierter Individualverkehr: 35 %
Fußgänger: 35 %
ÖPNV: 15 %
Fahrrad: 15 %
Fußgänger: 35 %
ÖPNV: 15 %
Fahrrad: 15 %
B: = „Von 100 befragten Schülern nutzten mindestens 20 den ÖPNV.“
C: = „Unter 80 befragten Schülern waren mindestens 20 und höchstens 30 Fußgänger.“
a)
Gib drei Bedingungen an, unter denen zur Berechnung für die Wahrscheinlichkeiten dieser Ereignisse das Modell der Binomialverteilung angenommen werden kann.
Zur Auswertung der Befragung wird das Modell der Binomialverteilung angewendet.
(3 BE)
b)
Berechne die Wahrscheinlichkeiten der Ereignisse 
 und
und  .
.
(6 BE)
c)
Beschreibe in diesem Sachzusammenhang ein Ereignis  , dessen Wahrscheinlichkeit durch
, dessen Wahrscheinlichkeit durch
berechnet werden kann.
berechnet werden kann.
(3 BE)
d)
Schüler eines anderen Gymnasiums wollen überprüfen, ob an ihrer Schule auch 15 % der Schüler mit dem Fahrrad zur Schule kommen.
Dazu befragen sie 100 Schüler. Berechne für das Prognoseintervall, in dem die Anzahl der Radfahrer mit einer Sicherheitswahrscheinlichkeit von 95 % liegt.
das Prognoseintervall, in dem die Anzahl der Radfahrer mit einer Sicherheitswahrscheinlichkeit von 95 % liegt.
Dazu befragen sie 100 Schüler. Berechne für
(3 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
b)
Das Kreuzprodukt der beiden Richtungsvektoren  und
und  liefert einen Normalenvektor
liefert einen Normalenvektor 
 der Ebene.
der Ebene.
Nun wird mit den Einträgen des Normalenvektors und die Koordinatenform aufgestellt:
und die Koordinatenform aufgestellt:  Einsetzen eines Punktes der Ebene liefert den Wert von
Einsetzen eines Punktes der Ebene liefert den Wert von  Einsetzen des Koordinaten des Punktes
Einsetzen des Koordinaten des Punktes  ergibt mit
ergibt mit 
 Für die Ebenengleichung folgt:
Für die Ebenengleichung folgt:

Nun wird mit den Einträgen des Normalenvektors
c)
Ein Normalenvektor der  Ebene lautet
Ebene lautet  . Mit dem gegebenen Normalenvektor
. Mit dem gegebenen Normalenvektor  der Ebene
der Ebene  folgt:
folgt:







d)
Die Koordinaten des Punktes  haben die Form
haben die Form  Somit folgt:
Somit folgt:


 Gleichsetzen liefert:
Gleichsetzen liefert:


 Mit dem solve-Befehl des CAS folgt nun:
Mit dem solve-Befehl des CAS folgt nun:
 Somit gilt
Somit gilt 
e)
f)
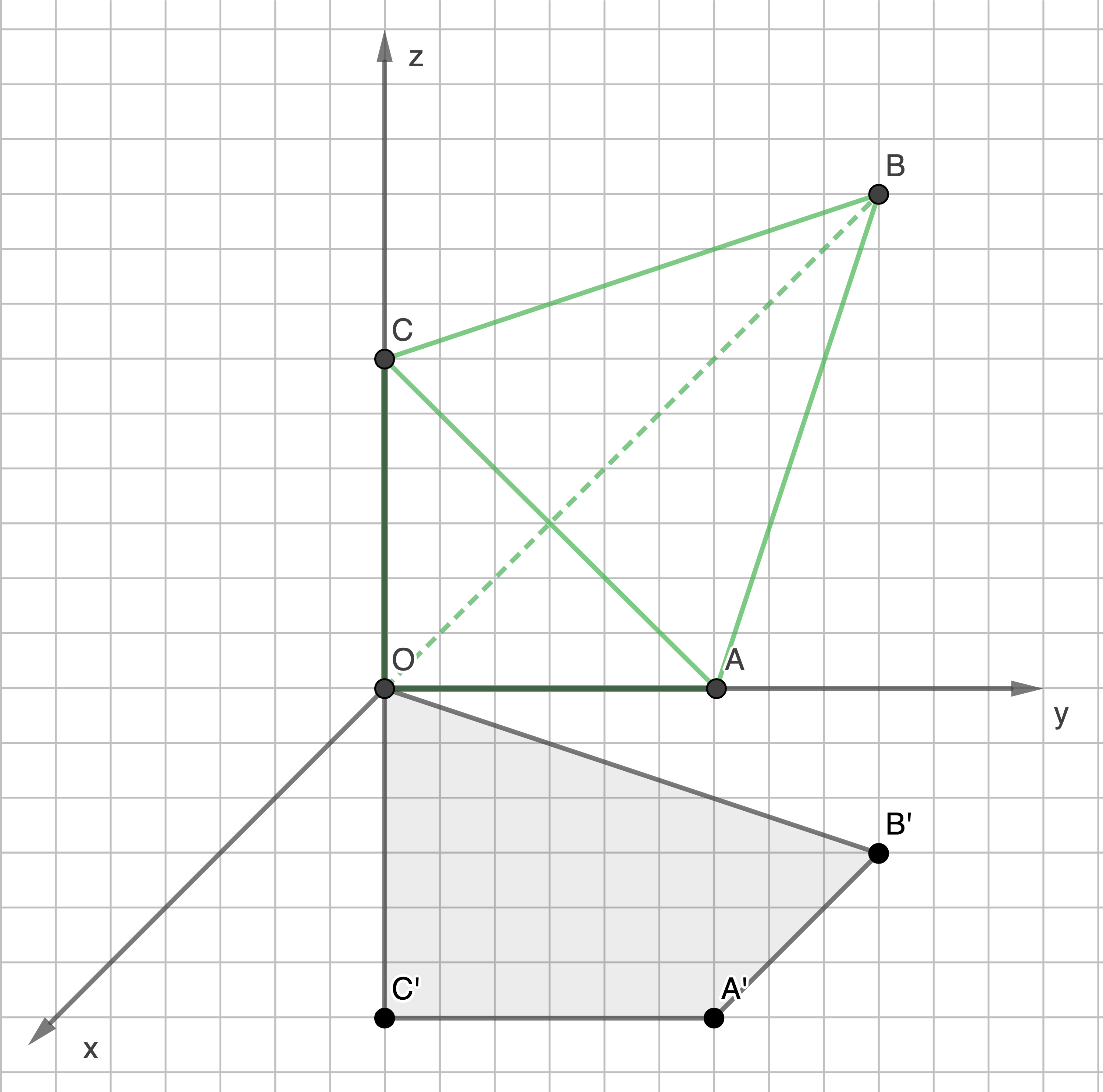
Abb.: Pyramide mit Projektion auf die xy-Ebene
g)
Aus der Skizze geht hervor, dass wenn  als Stützpunkt der Ebene gewählt wird und
als Stützpunkt der Ebene gewählt wird und  und
und  mit
mit 

 als Spannvektoren gewählt werden, die resultierende Ebene die Pyramide, aufgrund der Gleichseitigkeit des Dreiecks
als Spannvektoren gewählt werden, die resultierende Ebene die Pyramide, aufgrund der Gleichseitigkeit des Dreiecks  mittig zerteilt.
Eine mögliche Parametergleichung ergibt sich somit wie folgt:
mittig zerteilt.
Eine mögliche Parametergleichung ergibt sich somit wie folgt:



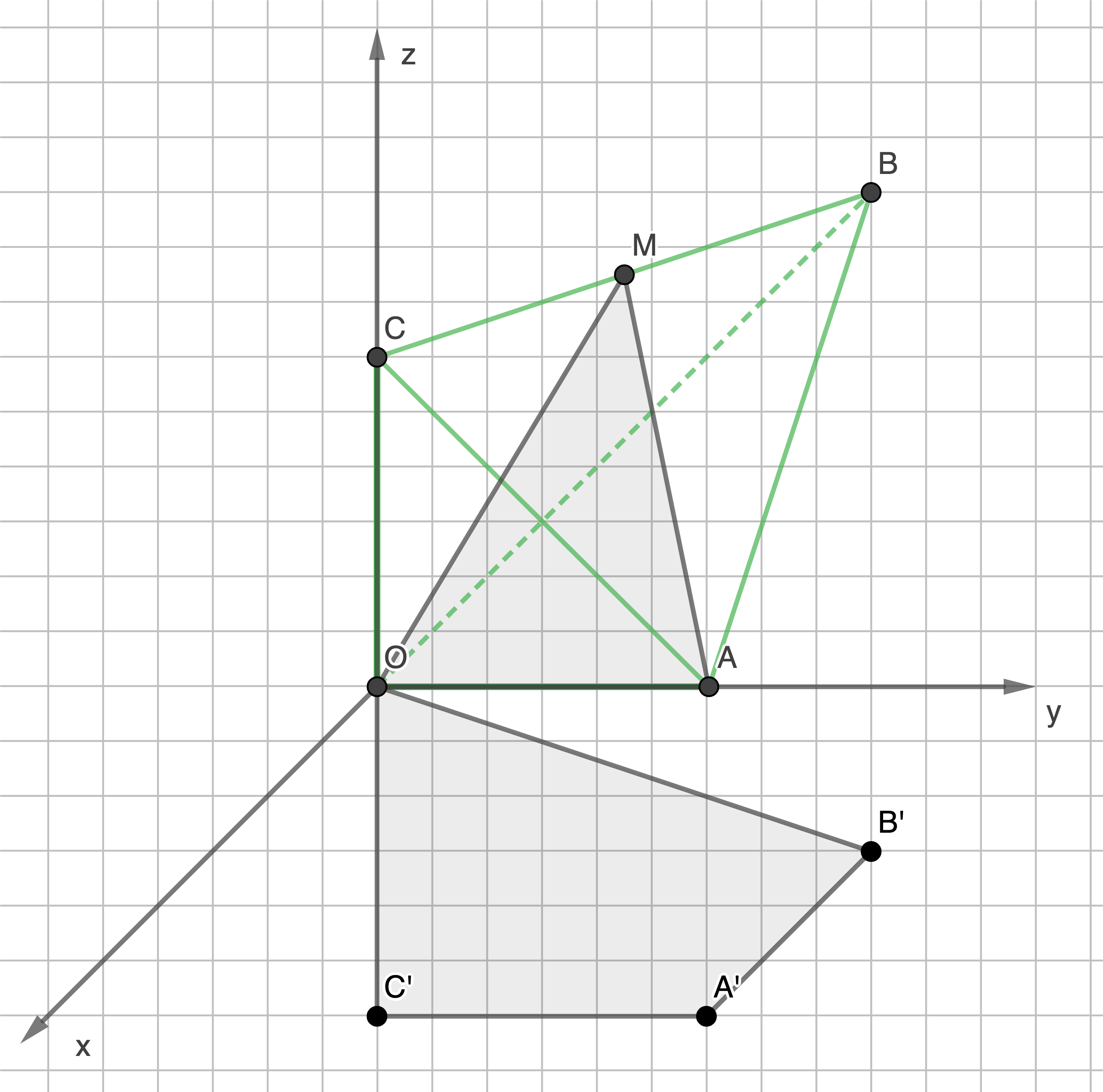

Abb.: Pyramide mit Projektion auf die xy-Ebene und flächenhalbierender Ebene
2
a)
- Die Anzahl
der befragten Schüler ist groß.
- Die Schüler werden unabhängig voneinander befragt.
- Nur eine Antwort ist möglich.
b)
Die Zufallsvariable  beschreibt die Anzahl der Schüler, die auf die jeweils gefragte Weise die Schule erreichten.
beschreibt die Anzahl der Schüler, die auf die jeweils gefragte Weise die Schule erreichten.











c)
Von 15 befragten Schülern sind höchstens 13 zu Fuß zur Schule gekommen.
d)
Anwenden der  -Regel:
-Regel: 








 Somit ist das Prognoseintervall
Somit ist das Prognoseintervall ![\([8 ; 22].\)](https://mathjax.schullv.de/3e6a49301440ade2c929b1fde5de18a37786a736f9e0d9220b01387782ac2f2d?color=5a5a5a)