Teil C2

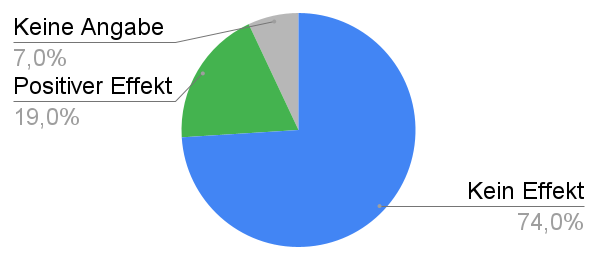
In einer Zufallsstichprobe wurden 1009 volljährige Thüringer befragt. 74 % der Befragten bezweifeln, dass eine $CO_2$ -Steuer zu einem geringeren $CO_2$ -Ausstoß führen würde. Nur 19 % erwarten einen positiven Effekt auf die $CO_2$ -Bilanz.

Die Befragung zeigt auch, dass die Thüringer bereit sind, selbst zur Senkung des $CO_2$ -Ausstoßes beizutragen. Von den Befragten wollen

54 % häufiger zu Fuß gehen,
48 % häufiger das Fahrrad nutzen,
45 % öfter auf öffentliche Verkehrsmittel umsteigen.

$\quad\quad$ Nach: OTZ. 26.08.2019, Seite 1.

Stelle die Befragungsergebnisse zur $CO_2$ -Steuer in einem Kreisdiagramm dar.
Begründe, dass diese Art der Darstellung für die Befragung zur Bereitschaft, persönlich zur Senkung des $CO_2$ -Ausstoßes beizutragen, nicht möglich ist.

(3 BE)

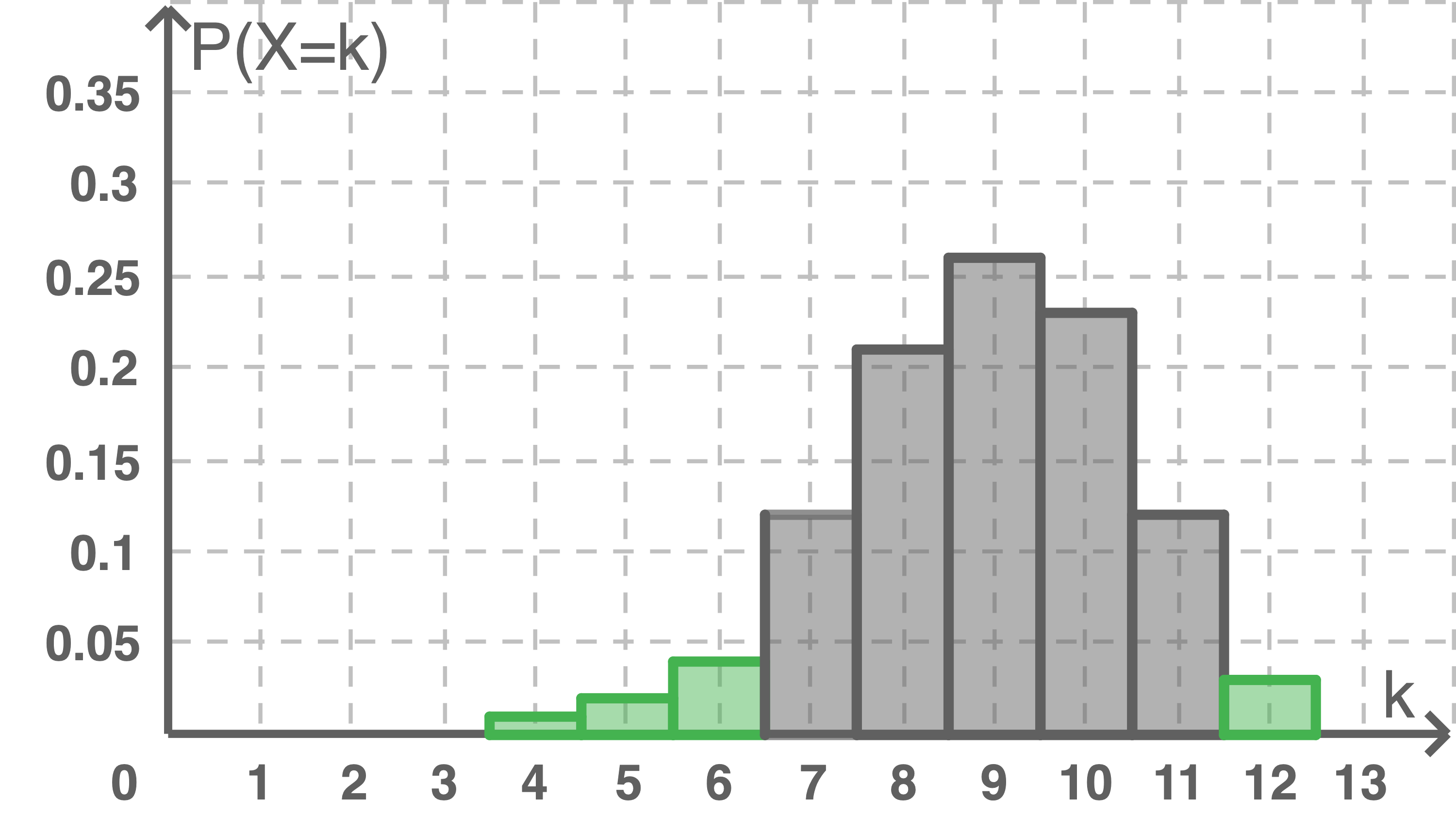
Gegeben ist die nebenstehende Darstellung einer Binomialverteilung.

Begründe, dass die Angaben zur $CO_2$ -Steuer als Grundlage dieser Modellierung dienen können.

Beschreibe ein Ereignis, das in der Darstellung durch die grau markierte Fläche mathematisch beschrieben wird.

thüringen mathe abi 2021 teil c2 abbildung 1

(5 BE)

Anita möchte Voraussagen für ihren eigenen Jahrgang treffen. Dafür nutzt sie die Befragungsergebnisse zur Bereitschaft, selbst zur Senkung des $CO_2$ -Ausstoßes beizutragen und verwendet das Modell der Binomialverteilung.
Zu ihrem Jahrgang gehören 60 Jugendliche.

Begründe, dass die relativen Häufigkeiten aus der Befragung als Trefferwahrscheinlichkeiten $p$ der zugehörigen Binomialverteilung interpretiert werden können.

(1 BE)

Berechne die Wahrscheinlichkeit folgender Ereignisse:
A = :„Weniger als 40 Jugendliche ihres Jahrgangs wollen häufiger zu Fuß gehen.“
B = :„Mindestens die Hälfte und höchstens drei Viertel der Jugendlichen ihres Jahrgangs wollen häufiger das Fahrrad nutzen.“
C = :„Die Anzahl der Jugendlichen ihres Jahrgangs, die bereit sind, häufiger das Fahrrad zu benutzen, liegt außerhalb der $1\sigma$ -Umgebung um den Erwartungswert.“

(8 BE)

Bestimme die Anzahl von Personen, die mindestens befragt werden müssen, damit mit einer Wahrscheinlichkeit von mindestens 90 % mindestens 50 der Befragten angeben, häufiger das Fahrrad zu benutzen.

(3 BE)

Anita nimmt weiterhin an, dass auch an ihrer Schule 48 % der Jugendlichen häufiger das Fahrrad nutzen wollen. Vor der Befragung der 60 Jugendlichen ihres Jahrgangs interessiert sie sich für das Intervall, in dem mit einer Wahrscheinlichkeit von 95 % die Anzahl derer liegt, die bereit sind, häufiger das Fahrrad zu nutzen.
Berechne das zugehörige Prognoseintervall für die Anzahl dieser Jugendlichen.
Beschreibe seine Bedeutung im Sachzusammenhang.

(5 BE)

Gegeben sind die Gerade $g$ durch:
$g: \overrightarrow{x}=\pmatrix{-1\\-1\\4}+r\cdot\pmatrix{-1\\-1\\2}\quad(r\in\mathbb{R})$ und für jede reelle Zahl $a$ die Gerade $h_a$ durch
$h_a:\overrightarrow{x}=\pmatrix{0\\0\\0}+s\cdot\pmatrix{3\\3\\a}\quad(s\in\mathbb{R}).$

Zeige, dass die Gerade $g$ und $h_{-6}$ parallel zueinander verlaufen, aber nicht identisch sind.

(2 BE)

Berechne den Abstand der Geraden $g$ und $h_{-6}.$

(3 BE)

Es gibt eine Zahl $a$ , so dass sich die Graphen $g$ und $h_a$ unter einem rechten Winkel schneiden.
Berechne diesen Wert von $a$ und bestimme die Koordinaten des zugehörigen Schnittpunkts.

(5 BE)

Die Geraden $h_a$ liegen alle in einer Ebene $\epsilon.$

Gib zwei Eigenschaften für die Lage der Ebene $\epsilon$ im Raum an.
Bestimme eine Gleichung der Ebene $\epsilon$ in Koordinatenform.

(5 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Kreisdiagramm mit Prozentangaben zu verschiedenen Effekten: kein Effekt, positiver Effekt, keine Angabe.

Die Befragung zur Bereitschaft persönlich zur Senkung des $CO_2$ -Ausstoßes beizutragen lässt sich nicht in einem Kreisdiagramm darstellen, denn die Kategorien schließen sich nicht gegenseitig aus, das heißt Mehrfachnennungen sin möglich.

Modellierung begründen

Die gegebene Binomialverteilung gibt die Wahrscheinlichkeit an, dass sich k von 12 befragten Thüringern für die Nutzlosigkeit der $CO_2$ -Steuer aussprechen.
Die Darstellung passt zu den Angaben der $CO_2$ -Steuer, da der Erwartungswert durch $\mu=12\cdot0,74=8,88$ gegeben ist und somit mit der Position des höchsten Balkens im Diagramm, bei $k=9,$ übereinstimmt.

Ereignis beschreiben

Ein Ereignis, welches die graue Fläche des Diagramms beschreibt, ist, dass sich von 12 Befragten mindestens 7 aber höchstens 11 für die Nutzlosigkeit der $CO_2$ -Steuer aussprechen.

Die Anzahl der Befragten ist mit $n=1009$ ausreichend groß.

Die Zufallsvariable $X$ beschreibt die Anzahl der Jugendlichen, die häufiger zu Fuß gehen wollen.

$P(A) = B_{60;0,54}(X \leq 39)$ $\approx 0,9681$ $= 96,81\,\%$

Die Zufallsvariable $X$ beschreibt nun die Anzahl der Jugendlichen, die häufiger das Fahrrad nutzen wollen.

$P(B) = B_{60;0,48}(30 \leq X \leq 45)$ $= P(X \leq 45) - P(X \leq 29)$ $\approx 0,4277$ $= 42,77\,\%$

$P(C)$ $= 1-B_{60;0,48}((\mu - \sigma) \leq x \leq (\mu + \sigma))$

$\mu = n \cdot p$ $= 60\cdot0,48$ $\approx 28,8$

$\sigma = \sqrt{ n \cdot p \cdot (1-p)}$ $= \sqrt{60 \cdot 0,48 \cdot 0,52}$ $\approx 3,9$

Das $1 \sigma$ Intervall ist somit gegeben durch $[24 \mathrm{,}9; 32\mathrm{,}7].$ Es folgt:

$P(C)$ $= 1-B_{60;0,48}((\mu - \sigma) \leq x \leq (\mu + \sigma))$ $= 1-B_{60;0,48}(25 \leq x \leq 32)$ $\approx 0,3026$ $= 30,26\,\%$

Die Zufallsvariable $X$ beschreibt die Anzahl an Personen die angeben, häufiger das Fahrrad zu benutzen.

$B_{n;0,48}(X \geq 50) \geq 0,90$

Dieser Audruck lässt sich mit Hilfe des Gegenereignisses wie folgt umformen:

$B_{n;0,48}(X \leq 49) \lt 0,10$

Systematisches Ausprobieren im Taschenrechner ergibt:

$\color{#fff}{n}$	$\color{#fff}{P(X \lt 49)}$
$117$	$0,109$
$118$	$0.094$

Somit müssen mindestens $118$ Leute befragt werden, damit mit einer Wahrscheinlichkeit von mindestens $90\,\%$ mindestens $50$ der Befragten angeben, häufiger das Fahrrad zu benutzen.

Anwenden der $2\sigma-$ Regel: $P(\mu - 2\sigma \leq x \leq \mu + 2\sigma)$

$\mu=n\cdot p=60\cdot 0,48=28,8$

$\sigma=\sqrt{n\cdot p\cdot(1-p)}$ $=\sqrt{60\cdot0,48\cdot0,52}\approx3,87$

Somit ist das Prognoseintervall gegeben durch $[22;36].$

Mit einer Wahrscheinlichkeit von $95\,\%$ wird erwartet, dass zwischen 22 und 36 dieser Jugendlichen häufiger Fahrrad fahren.

Parallelität zeigen

$k\cdot\pmatrix{-1\\-1\\2} = \pmatrix{3\\3\\-6}$

Lösung des zugehörigen Gleichungssystems im CAS liefert $k = -3.$ Somit sind die beiden Geraden parallel zueinander.

Identität widerlegen

Punktprobe:

$\pmatrix{-1\\-1\\4}$ $= \pmatrix{0\\0\\0}$ $+ s \cdot \pmatrix{3\\3\\-6}$

Der CAS liefert keine Lösung für das zugehörige Gleichungssystem, somit sind die beiden Geraden nicht identisch.

Da nach Teilaufgabe a) die beiden Geraden parallel zueinander verlaufen, kann ein beliebiger Punkt auf $g$ gewählt werden, um den Abstand zu berechnen.

$G(-1 \mid -1 \mid 4)$

Hilfsebene $H$ aufstellen:

$H: \; \left( \pmatrix{-1\\-1\\4} - \vec{x} \right) \circ \pmatrix{-1\\-1\\2} = 0$

Es ergibt sich folgender Schnittpunkt von der Hilfsebene $H$ mit der Geraden $h$ :

$S \left( \dfrac{-5}{3} \; \biggr\rvert \; \dfrac{-5}{3} \; \biggr\rvert \; \dfrac{10}{3} \right)$

Für den Abstand der beiden Geraden folgt somit:

$d$ $= \vert\overrightarrow{SG}\vert$ $= \sqrt{ \left( -\dfrac{2}{3} \right)^2 +\left( -\dfrac{2}{3} \right)^2 +\left( \dfrac{2}{3} \right)^2 }$ $\approx 1,16$

Wert von $a$ berechnen

Damit sich zwei Geraden parallel schneiden, müssen unter anderem die Richtungsvektoren senkrecht aufeinander stehen. Es folgt:

$\begin{array}[t]{rll} \pmatrix{-1\\-1\\2} \circ \pmatrix{3\\3\\a}&=0& \; \\[5pt] -3-3+2a&=0& \; \\[5pt] a&=3& \end{array}$

Koordinaten des Schnittpunkts bestimmen

$\pmatrix{-1\\-1\\4}$ $+ r\cdot\pmatrix{-1\\-1\\2}$ $= \pmatrix{0\\0\\0}$ $+ s\cdot\pmatrix{3\\3\\3}$

Lösen des zugehörigen LGS im CAS ergibt:

$r= -\dfrac{5}{3}$

$s= \dfrac{2}{9}$

Die Koordinaten des Schnittpunkts ergeben sich damit wie folgt:

$S \left( \dfrac{2}{3} \; \biggr\rvert \; \dfrac{2}{3} \; \biggr\rvert \; \dfrac{2}{3} \right)$

Eigenschaften angeben

Die Ebene $\varepsilon$ steht senkrecht auf der $xy$ -Ebene
Die Ebene $\varepsilon$ enthält die Winkelhalbierende zwischen positiver $x$ - und $y$ -Achse

Ebenengleichung in Koordinatenform bestimmen

Als ein Normalenvektor ergibt sich $\overrightarrow{n}$ $= \pmatrix{3\\-3\\0},$ da $\overrightarrow{n}$ für alle $a \in \mathbb{R}$ orthogonal zu $\pmatrix{3\\3\\a}$ ist.

Es folgt:

$\varepsilon:3x-3y=d$

Einsetzen eines Punktes der Ebene, zum Beispiel des Koordinatenursprungs, liefert:

$d=3\cdot0-3\cdot0 = 0$

Somit ergibt sich:

$\varepsilon: \; 3 x - 3 y = 0$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?