Teil A
1
Gib in der Tabelle je eine zugehörige Funktionsgleichung an.
Funktionsgleichung von  |
Funktionsgleichung von  |
|---|---|
 |
|
 |
|
 |
|
 |
|
 |
(5 BE)
2
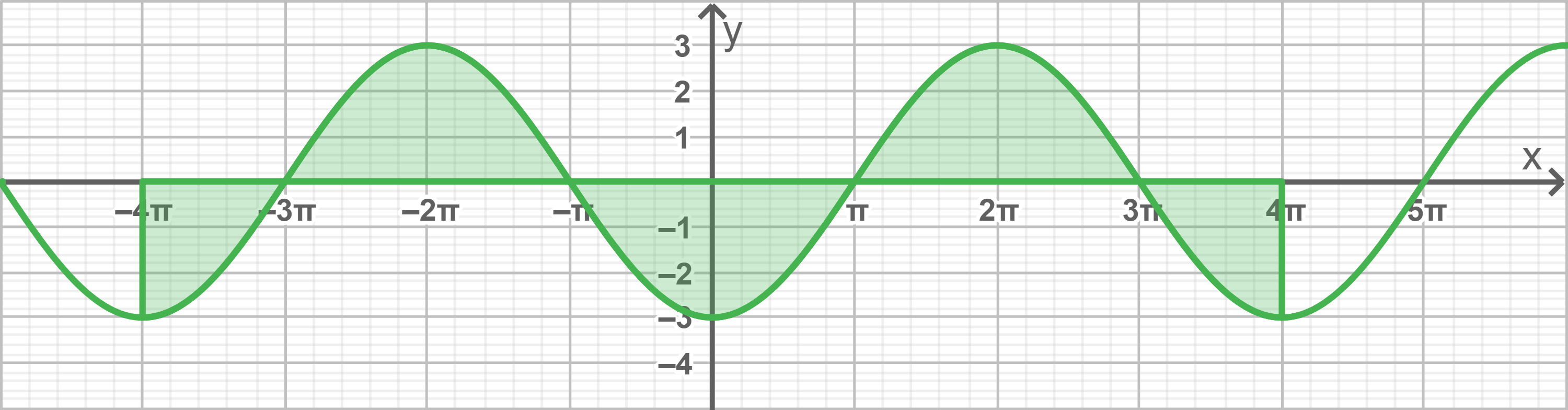
Gegeben ist der Graph einer Funktion 
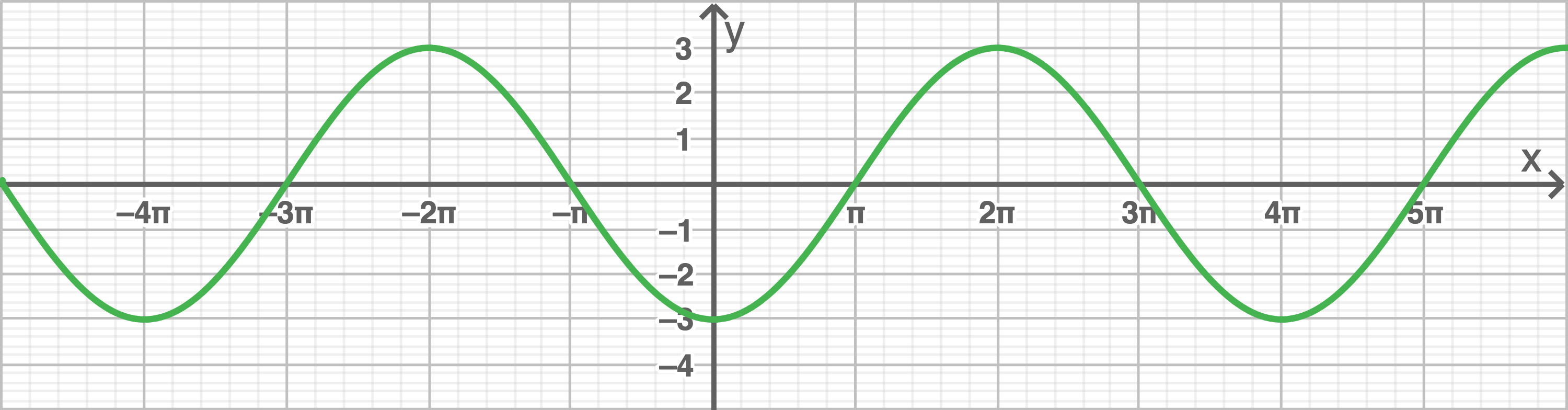
a)
Gib eine passende Funktionsgleichung für 
an.
an.
(3 BE)
b)
Veranschauliche mit Hilfe von Flächen in der obigen Darstellung 
Gib den Wert des Integrals an.
Gib den Wert des Integrals an.
(2 BE)
3
Gegeben sind für 
die Funktionen mit 
und 
mit 
die Funktionen mit und mit
a)
Zeige, dass der Graph von die Tangente an den Graphen von im Punkt 
ist.
die Tangente an den Graphen von im Punkt ist.
(2 BE)
b)
Bestimme den Flächeninhalt der markierten Fläche 
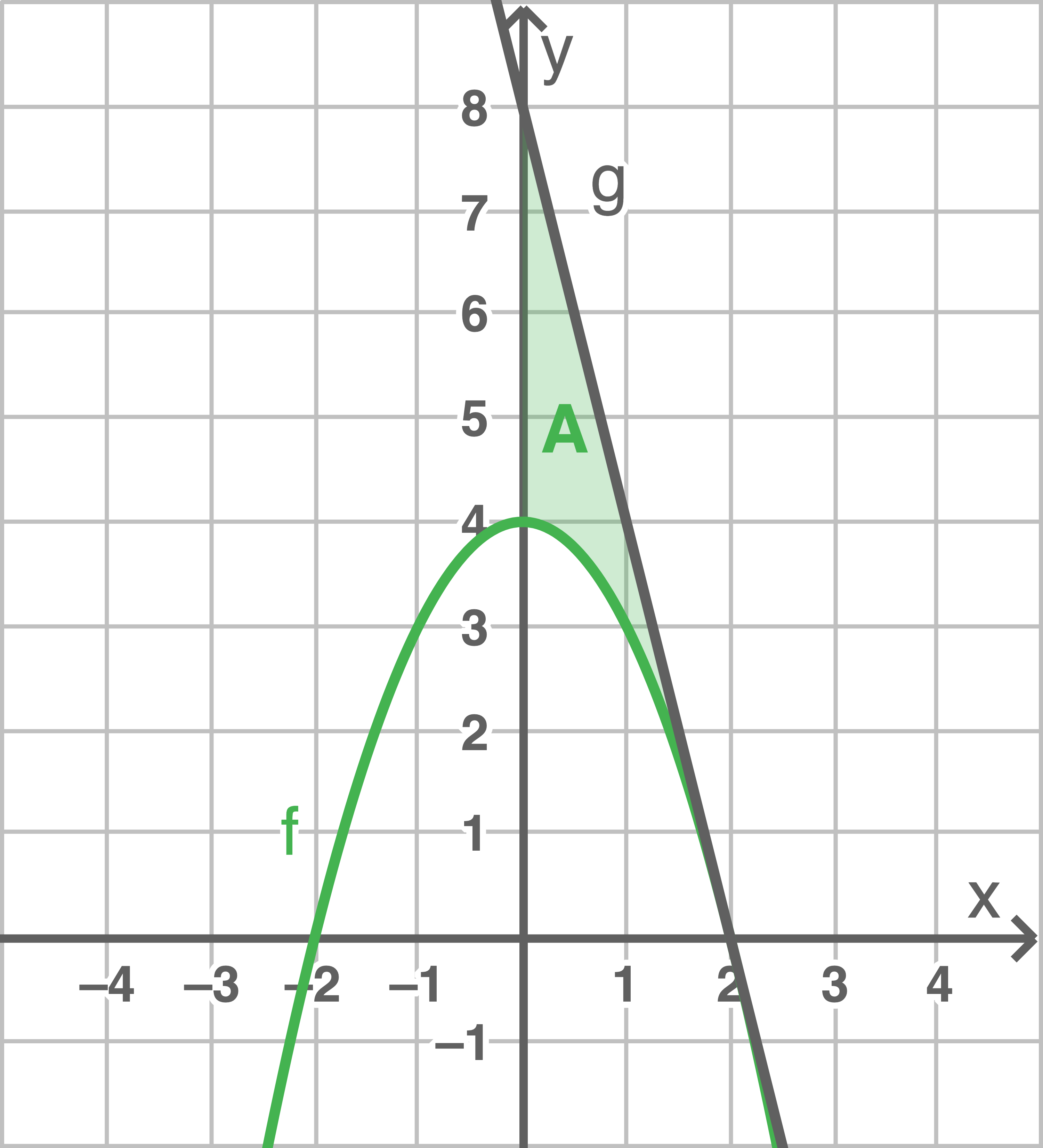
(3 BE)
4
Der Graph der Funktion entsteht, wenn der Graph von mit 
um 
verschoben wird.
entsteht, wenn der Graph von mit um verschoben wird.
a)
Gib eine Gleichung von an.
an.
(1 BE)
b)
Der Graph von , die Koordinatenachsen und die Gerade 
begrenzen eine Fläche vollständig. Zur Berechnung des Flächeninhalts wird der Ansatz 
vorgeschlagen.
Bewerte diesen Ansatz und berechne den Flächeninhalt.
, die Koordinatenachsen und die Gerade begrenzen eine Fläche vollständig. Zur Berechnung des Flächeninhalts wird der Ansatz vorgeschlagen.
Bewerte diesen Ansatz und berechne den Flächeninhalt.
(4 BE)
5
Die Punkte 
und 
mit 
sind Eckpunkte einer geraden Pyramide mit rechteckiger Grundfläche und der Höhe 
.
und mit sind Eckpunkte einer geraden Pyramide mit rechteckiger Grundfläche und der Höhe .
a)
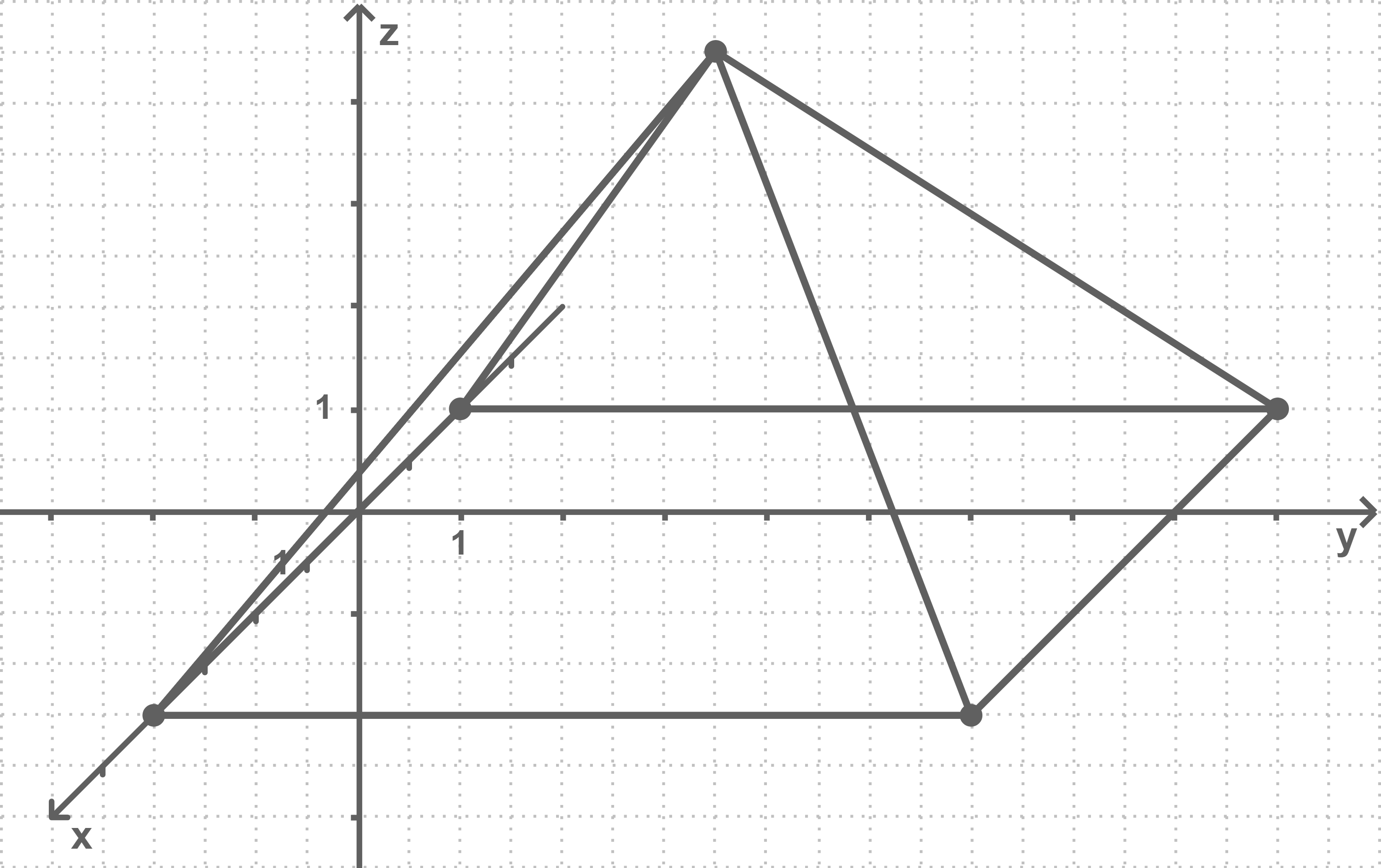
Zeichne eine solche Pyramide in ein Koordinatensystem.
(2 BE)
b)
Die Länge einer Seitenkante soll 
betragen.
Bestimme die Höhe dieser Pyramide.
betragen.
Bestimme die Höhe
dieser Pyramide.
(3 BE)
6
Die Vektoren 
und 
spannen eine gerade Pyramide auf.
und spannen eine gerade Pyramide auf.
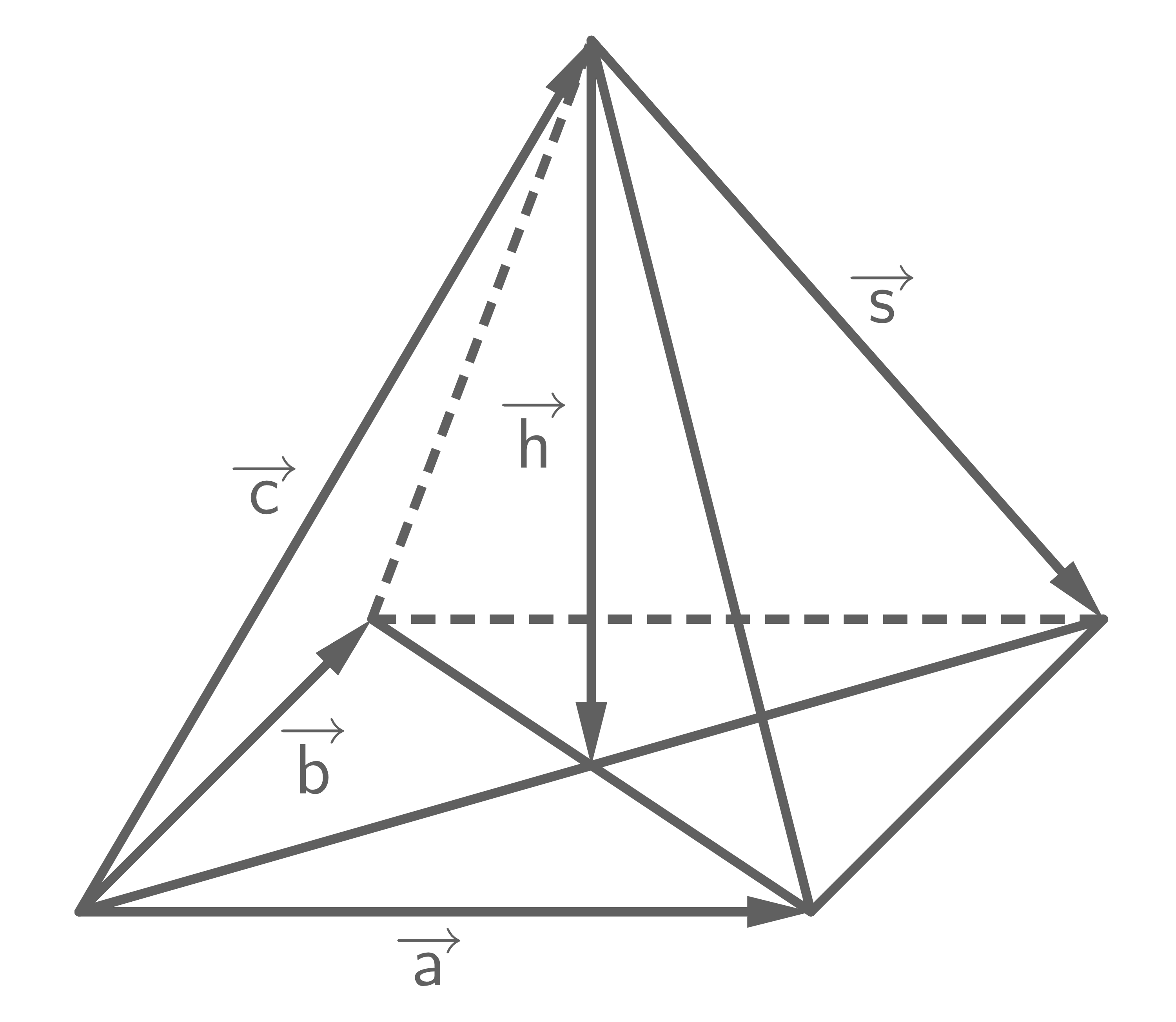
a)
Gib die Vektoren 
und 
mit Hilfe der Vektoren und an.
und mit Hilfe der Vektoren und an.
(2 BE)
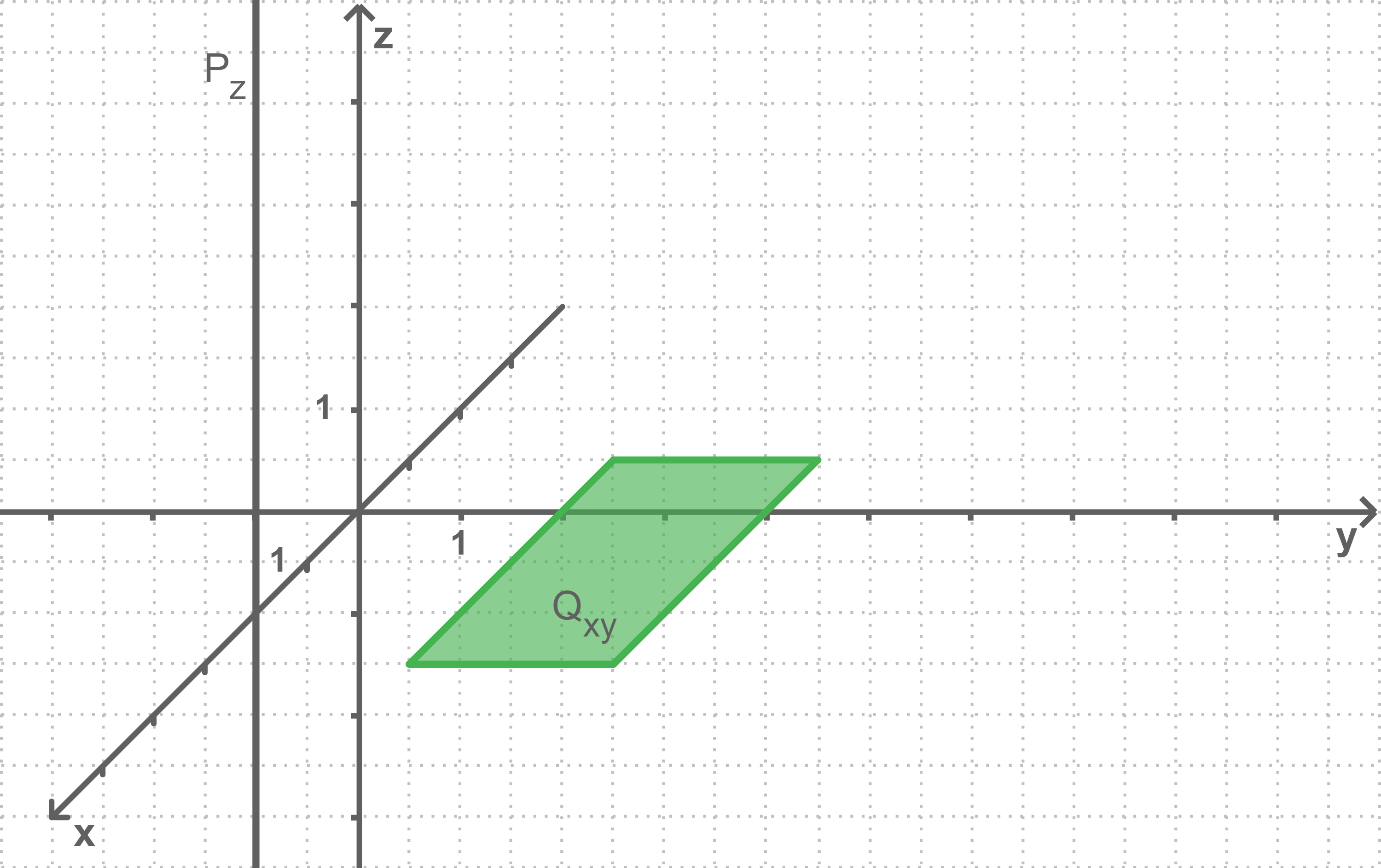
b)
Durch 
mit 
wird eine Punktmenge 
beschrieben.
Eine weitere Punktmenge
wird durch 
mit 
und 
beschrieben.
Veranschauliche die Punktmengen im Koordinatensystem.
mit wird eine Punktmenge beschrieben.
Eine weitere Punktmenge
wird durch mit und beschrieben.
Veranschauliche die Punktmengen im Koordinatensystem.
(3 BE)
7
In einer Box befinden sich zehn Kugeln, von denen zwei rot sind.
Es werden zufällig nacheinander zwei Kugeln gezogen, in einem ersten Experiment mit Zurücklegen und in einem zweiten Experiment ohne Zurücklegen.
Es werden zufällig nacheinander zwei Kugeln gezogen, in einem ersten Experiment mit Zurücklegen und in einem zweiten Experiment ohne Zurücklegen.
a)
Zeige, dass die Wahrscheinlichkeit des Ereignisses 
= „Die zweite Kugel ist rot.“ bei beiden Experimenten 
beträgt.
= „Die zweite Kugel ist rot.“ bei beiden Experimenten beträgt.
(2 BE)
b)
Die Anzahl der roten Kugeln unter den zehn Kugeln in der Box soll so verändert werden, dass sich die Wahrscheinlichkeit des Ereignisses 
beim Ziehen mit Zurücklegen auf 
erhöht.
Bestimme die Anzahl der benötigten roten Kugeln.
beim Ziehen mit Zurücklegen auf erhöht.
Bestimme die Anzahl der benötigten roten Kugeln.
(3 BE)
8
Es sei 
eine normalverteilte Zufallsgröße mit Erwartungswert 
und Standardabweichung 
.
eine normalverteilte Zufallsgröße mit Erwartungswert und Standardabweichung .
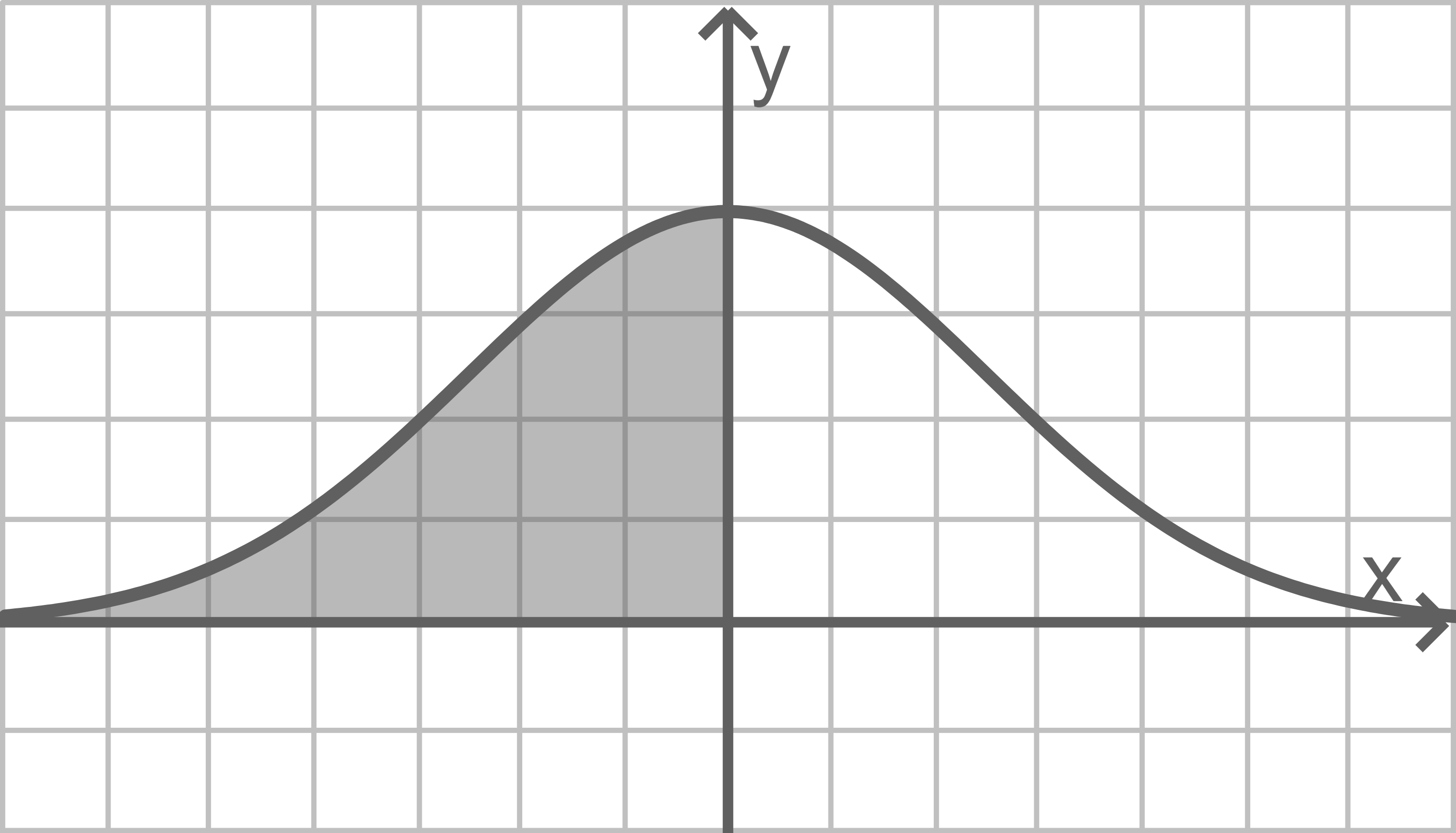
a)
Erläutere anhand einer Skizze, dass 
gilt.
gilt.
(3 BE)
b)
Es ist bekannt, dass 
.
Bestimme
.
.
Bestimme
.
(2 BE)
1
2
a)
b)
gilt.
3
a)
Es folgt:
Weiter gilt:
b)
![\(\begin{array}[t]{rll}
A&=&\displaystyle\int_{0}^{2}\left(g(x)-f(x)\right)\;\mathrm dx \\[5pt]
&=&\displaystyle\int_{0}^{2}\left(x^2-4x+4\right)\;\mathrm dx \\[5pt]
&=&\left[\dfrac{1}{3}x^3-2x^2+4x\right]^2_0 \\[5pt]
&=&\dfrac{1}{3}\cdot2^3-2\cdot2^2+4\cdot 2-0 \\[5pt]
&\approx&2,67\;[\text{FE}]
\end{array}\)](https://www.schullv.de/resources/formulas/09783aaadb4d17819e42724b3eae2690f880126a1777c79d4c77828075e75213_light.svg)
4
a)
b)
Der Ansatz ist korrekt, denn aufgrund der Verschiebung gilt:
![\(\begin{array}[t]{rll}
A&=& \displaystyle\int_{1}^{4}g(x)\;\mathrm dx \\[5pt]
&=& \displaystyle\int_{-\,3}^{0}f(x)\;\mathrm dx \\[5pt]
&=& \left[\dfrac{2}{3}x^{\frac{3}{2}}\right]_{1}^{4} \\[5pt]
&=& \dfrac{2}{3}\cdot8-\dfrac{2}{3}\cdot1\\[5pt]
&\approx&4,67\;[\text{FE}]
\end{array}\)](https://www.schullv.de/resources/formulas/bd98ea34e9b743db7626ffd106888f89dc554812c244542af023cf2dd775337a_light.svg)
5
![\( h=12\;[\text{LE}] \)](https://www.schullv.de/resources/formulas/ea4c3dae9f2bc8c50ff51c6e801e0605cf4a6429d6a5fde37e7a7c992f1b0f80_light.svg)
![\(\begin{array}[t]{rll}
\left\vert\pmatrix{1-4\\4-0\\h-0}\right\vert&=& 13 \\[5pt]
\sqrt{(1-4)^2+4^2+h^2}&=& 13&\quad\scriptsize\mid\;^2 \\[5pt]
(1-4)^2+4^2+h^2&=& 169 \\[5pt]
25+h^2&=&169 &\quad\scriptsize\mid\;-25\\[5pt]
h^2&=& 144&\quad\scriptsize\mid\;\sqrt{\;}\\[5pt]
h&=& 12\;[\text{LE}]
\end{array}\)](https://www.schullv.de/resources/formulas/814e86ea78def2489e36e11aa73c5cabec2541cb526f20125dc39a19c87bc695_light.svg)
6
a)
b)
7
a)
b)
Ereignis tritt ein, wenn die erste Kugel weiß oder rot, und die zweite Kugel rot, ist:
Es folgt, dass die gesuchte Anzahl an roten Kugeln 
beträgt.
tritt ein, wenn die erste Kugel weiß oder rot, und die zweite Kugel rot, ist:
Es folgt, dass die gesuchte Anzahl an roten Kugeln beträgt.
8
a)
b)
Es gilt 
Somit folgt:
Somit folgt: