Teil B

Gegeben sind mit $x \in\mathbb{R}$ die Funktion $f$ durch $f(x)= \dfrac{1}{10}x^2 \cdot (x-6)$ und für jede reelle Zahl $a$ $( a\neq 0)$ eine Funktion $g_a$ durch $g_a (x)= f(x)+a \cdot x.$

Zeige, dass $x=2$ die Wendestelle von $f$ ist.

(2 BE)

Begründe, dass die Funktionen $f$ und $g_a$ für alle Werte von $a$ eine gemeinsame Wendestelle besitzen.

(2 BE)

Weise nach, dass sich die Wendetangente an den Graphen von $f$ und alle Wendetangenten an die Graphen von $g_a$ in einem gemeinsamen Punkt schneiden.

(4 BE)

Die Punkte $P \left(0 \mid \frac{4}{5}\right)$ , $W_f(2 \mid f(2))$ und $W_{g_a}(2 \mid g_a(2))$ sind Eckpunkte eines Dreiecks. Untersuche, für welche Werte von $a$ dieses Dreieck rechtwinklig ist.

(6 BE)

Die Graphen von $f$ und $g_a$ sowie die Gerade $x=2$ begrenzen eine Fläche vollständig.
Bestimme alle Werte für $a$ so, dass der Inhalt dieser Fläche $10\,\text{FE}$ beträgt.

(3 BE)

Ein Unternehmen produziert E-Scooter.
Die monatlichen Produktionskosten der E-Scooter in Euro werden im Unternehmen mithilfe der Funktion $k$ mit $k(x)=\dfrac{1}{400}x^3-3x^2+1250x+50\,000$ mathematisch beschrieben.
Für den Erlös $e$ beim Verkauf der E-Scooter gilt der funktionale Zusammenhang $e(x)= p \cdot x,$ wobei $p$ der Stückpreis in Euro und $x$ die Stückzahl bedeuten. Der Gewinn $g$ eines Unternehmens lässt sich als Differenz aus dem Erlös $e$ und den Produktionskosten $k$ berechnen.

Für die folgenden Aufgaben wird vorausgesetzt, dass alle produzierten E-Scooter auch verkauft werden.

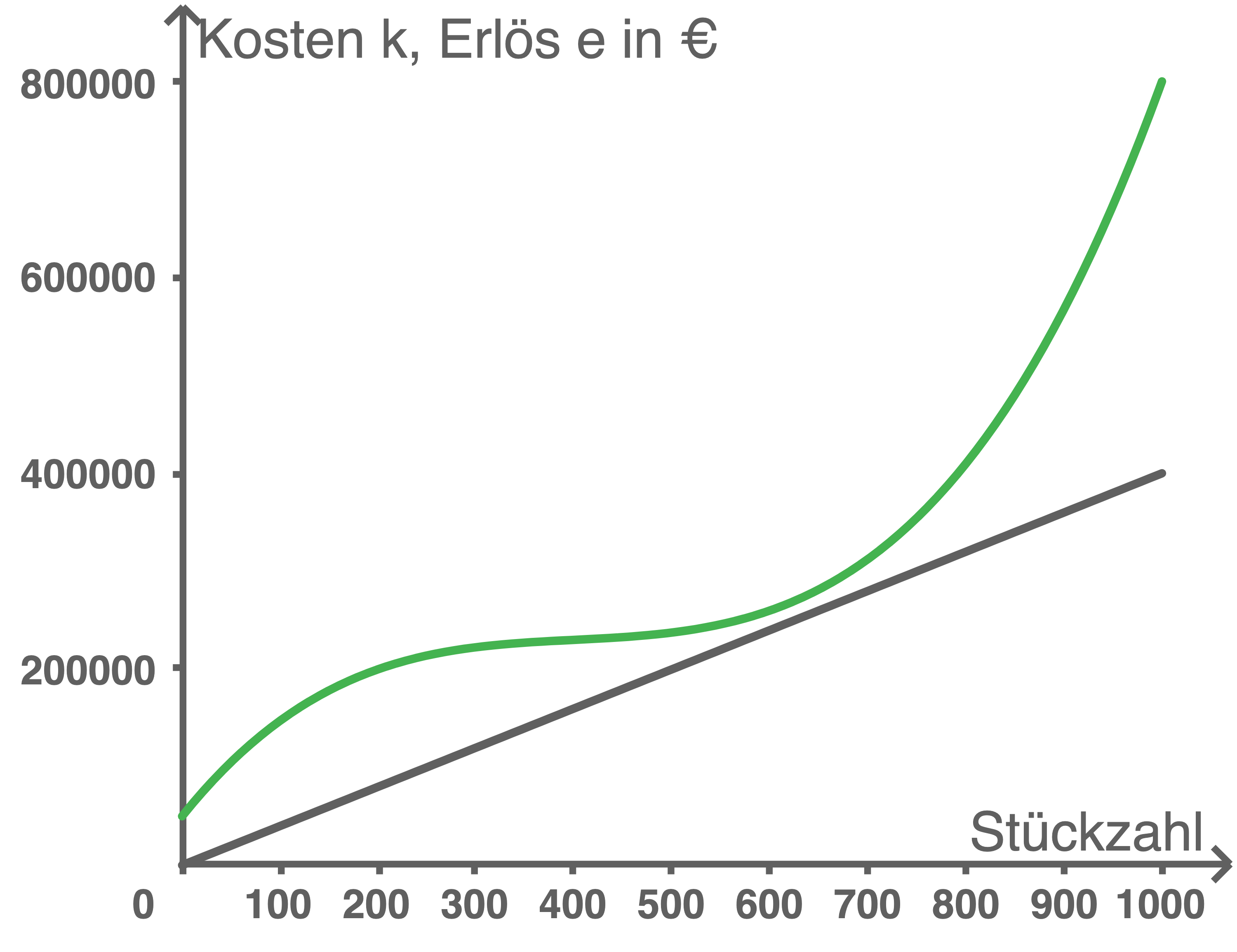
Dargestellt sind die Graphen der Funktionen $k$ und $e$ mit $p=400$ im Intervall $0\leq x\leq 1000$ .

Entscheide mithilfe der Graphen, ob der Stückpreis von $400\,€$ für das Unternehmen rentabel ist.
Begründe deine Entscheidung.

thüringen mathe abi 2020 teil b abbildung 1

(3 BE)

Im Unternehmen wird nach Analyse der Marktsituation entschieden, den Preis für einen E-Scooter auf $725\,€$ festzusetzen.

Bestimme die monatliche Mindest- und die Höchstanzahl von E-Scootern, damit Gewinn erwirtschaftet werden kann. Berechne den Maximalgewinn, den das Unternehmen erzielen kann.

(7 BE)

Die E-Scooter werden zu einem Preis von $725\,€$ verkauft.
Modellhaft kann der zugehörige Absatz mithilfe der Funktion $a$ mit $a(t)= 500 \cdot t\cdot \mathrm{e}^{-0,25\cdot t}$ $(t\in \mathbb{R} ;0 \leq t\leq 12)$ beschrieben werden. Dabei ist $t$ die seit der Produkteinführung vergangene Zeit in Monaten und $a(t)$ der Absatz in Stück pro Monat.

Ermittle die Monate, in denen der Absatz zunimmt.

(3 BE)

Die Produktionskosten bedingen, dass das Unternehmen mindestens $309$ Stück pro Monat verkaufen muss, um Gewinn zu erwirtschaften.
Bestimme den Zeitraum, in dem sich die Produktion lohnt.
Ermittle die Stückzahl der in den ersten elf Monaten verkauften E-Scooter sowie den Gesamterlös, den das Unternehmen aus dem Verkauf der E-Scooter in diesem Zeitraum erzielt.

(5 BE)

Es gibt einen Zeitpunkt, an dem der Absatz am stärksten zunimmt und einen Zeitpunkt, an dem er am stärksten abnimmt.
Zur Bestimmung dieser Zeitpunkte wird folgende Untersuchung durchgeführt:
$\(a$ hat nur die Lösung $t=8$ und es gilt $\(a$ .
Erläutere diese Untersuchung.
Gib den anderen Zeitpunkt an und begründe deine Angabe ohne weitere Rechnung.

(5 BE)

Ableiten der Funktion $f$ im CAS liefert:

$\(f$

Notwendiges Kriterium

$\(\begin{array}[t]{rll} f$

Da die Aufgabenstellung besagt, dass $f$ eine Wendestelle besitzt, muss die hinreichende Bedingung nicht überprüft werden.

Mit Hilfe des CAS ergibt sich die zweite Ableitung von $g_a$ als:

$\(g_a$

Die zweite Ableitung von $g_a$ stimmt mit der von $f$ überein, somit besitzen sie die selben Wendestellen.

Die Steigung $m$ der Wendetangente wird durch die erste Ableitung der Funktion an der Wendestelle gegeben:

$\(\begin{array}[t]{rll} f$

$\(\begin{array}[t]{rll} g_a$

Für die $y-$ Koordinaten der jeweiligen Wendepunkte folgt:

$\begin{array}[t]{rll} f(2)&=& \dfrac{1}{10}\cdot2^2\cdot(2-6) \\[5pt] &=&-\dfrac{8}{5} \end{array}$

$\begin{array}[t]{rll} g_a(2)&=&f(2)+a\cdot2 \\[5pt] &=&-\dfrac{8}{5}+2a \end{array}$

Einsetzen der Koordinaten der Wendepunkte in die Tangentengleichungen $y=m\cdot x+b$ liefert mit dem solve-Befehl des CAS für die jeweiligen Werte von $b:$

$t_f(x)$ $= -\dfrac{6}{5}x$ $+\dfrac{4}{5}$

$t_{g_a}(x)$ $= \left(a-\dfrac{6}{5} \right) x$ $+\dfrac{4}{5}$

Beide Tangenten haben den gleichen $y$ -Achsenabschnitt, somit schneiden sie sich im Punkt mit den Koordinaten $S=\left(0 \;\bigg \vert\; \dfrac{4}{5}\right)$

Im Fall, dass der rechte Winkel bei $P$ liegt, muss $\(f$ $=-1$ gelten. Es folgt:

Rechenweg anzeigen

$a=\dfrac{61}{30}$

Falls der rechte Winkel bei $W_{g_{a}}$ liegt, müssen $P$ und $W_{g_{a}}$ auf der selben Höhe liegen, das heißt es gilt $g_a(2)=\frac{4}{5}.$ In diesem Fall folgt:

Rechenweg anzeigen

$a=\dfrac{6}{5}$

Aus den Funktionsgleichungen folgt, dass $f(x)=g_a(x)$ für $x=0$ gilt. Die Grenzen des Integrals ergeben sich somit als $x=0$ und $x=2.$ Auflösen der Terme $\displaystyle\int_{0}^{2}f(x)-g_a(x)\;\mathrm dx$ $=10$ und $\displaystyle\int_{0}^{2}g_a(x)-f(x)\;\mathrm dx$ $=10$ nach $a$ im CAS liefert:

$a_1=-5$

$a_2=5$

Die Gerade entspricht dem Graphen von $e,$ welcher im gegebenen Intervall unterhalb des Graphen von $k$ liegt.
Der Stückpreis von $400€$ rentiert sich somit nicht, da für jede Stückzahl die Kosten größer als der Erlös sind.

Mit $p=725$ ergibt sich $g(x)=e(x)-k(x)$ als:

$g(x) = -\dfrac{1}{400}x^3+3x^2-525x-50000$

Bestimmung der Nullstellen mit dem solve-Befehl des CAS liefert:

$\begin{array}[t]{rll} x_1&\approx&308,3 \\[5pt] x_2&\approx&959,4 \end{array}$

Es werden somit mindestens $309$ und maximal $959$ E - Scooter verkauft.

Ableiten der Funktion $g$ im CAS liefert:

$\(g$

Mit Hilfe des solve-Befehls des CAS folgt für die Nullstellen von $\(g$

$\begin{array}[t]{rll} x_1&=&100 \\[5pt] x_2&=&700 \end{array}$

Einsetzen in $\(g$ liefert weiter:

$\(\begin{array}[t]{rll} g$

Die Funktion $g$ besitzt bei $x_2=700$ ein Maximum, somit wird der höchste Gewinn beim Verkauf von $700$ E-Scootern erzielt. Die Summe dieses Gewinns ergibt sich als $g(700) = 195000\,€.$

Ableiten der Funktion $a$ im CAS liefert:

$\(a$

Da die $\mathrm e$ -Funktion stets größer als null ist, ist der Funktionswert von $\(a$ genau dann größer als null, wenn $125t\lt500$ gilt. Da $t$ als Variable der Zeit keine negativen Werte annehmen kann, ist das für $0\leq t\lt4$ der Fall. Somit nimmt der Umsatz bis zum vierten Monat zu.

Zeitraum bestimmen

Gleichsetzen von $a(t)=500\cdot t\cdot\mathrm e^{-0,25t}$ mit $309$ und auflösen nach $t$ mit dem solve-Befehl des CAS liefert:

$\begin{array}[t]{rll} t_1&\approx&0,74 \\[5pt] t_2&\approx&11,80 \end{array}$

Da aus Aufgabenteil 2c) bekannt ist, dass der Graph von $a$ an der Stelle $t_1$ steigt, lohnt sich die Produktion zwischen ca. drei Wochen nach Beginn und kurz vor Ende des Produktionsjahres.

Stückzahl und Gesamterlös ermitteln

Integration über die Funktion $a$ im Intervall $[0;11]$ liefert für die Stückzahl der E-Scooter:

$\displaystyle\int_{0}^{11}a(t)\;\mathrm dt \approx 6082$

Multiplikation mit dem Einzelpreis liefert für den Gesamterlös:

$6082\cdot725\,€=4.409.450\,€$

In den ersten elf Monaten werden $6082$ E-Scooter produziert und ein Gesamterlös von $4,4\;\text{Mio.}\;€$ erwirtschaftet.

Der Graph von $a$ nimmt an seinen Wendestellen am stärksten zu bzw. ab.
Die Untersuchung liefert, dass der Graph bei $t=8$ seine einzige Wendestelle besitzt. Die Aussage $\(a$ besagt zusätzlich, dass dort ein lokales Minimum der Steigung vorliegt.
Da bei $t=8$ die einzige Wendestelle des Graphen von $a$ vorliegt, muss der Anstieg des Absatzes am Intervallrand bei $t=0$ am größten sein.