Teil A
1
Gib in der Tabelle je eine zugehörige Funktionsgleichung an.
| Funktionsgleichung von |
Funktionsgleichung von |
|---|---|
(5 BE)
2
Betrachtet wird eine Schar von Funktionen  mit
mit  und
und  .
.

a)
Gib die Nullstellen von  an.
an.
(2 BE)
b)
Entscheide, ob folgende Aussage wahr ist.
Begründe deine Entscheidung. „Es gibt Werte für so, dass die
so, dass die  -Achse Tangente an den Graphen von
-Achse Tangente an den Graphen von  ist."
ist."
Begründe deine Entscheidung. „Es gibt Werte für
(3 BE)
3
Für jeden Wert von  ist eine Funktion
ist eine Funktion  gegeben durch
gegeben durch 

a)
Beschreibe die Lage der Graphen von  bezogen auf den Graphen der Funktion
bezogen auf den Graphen der Funktion  mit
mit 
(2 BE)
b)
Berechne den Wert für  so, dass gilt:
so, dass gilt:

(3 BE)
4
Gegeben sind die Graphen der Funktionen  und
und 
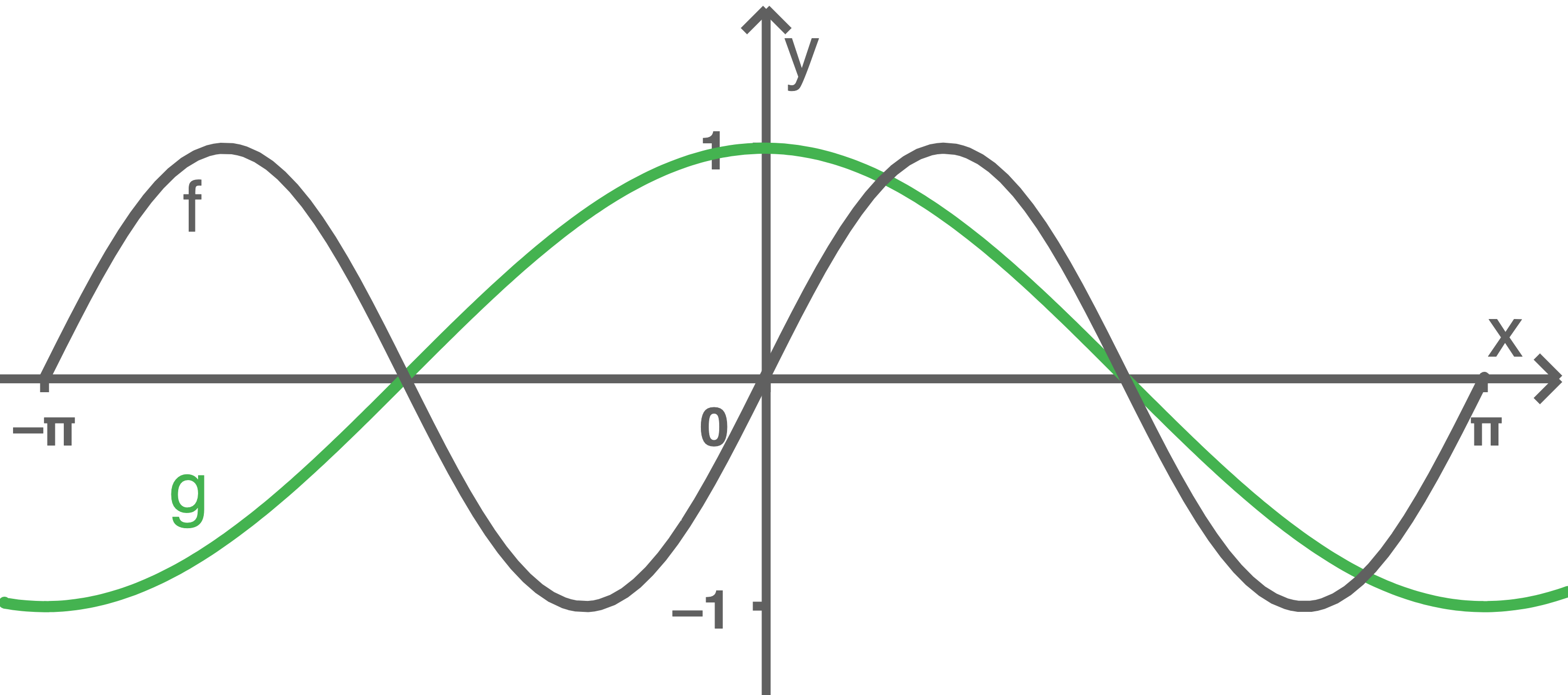

a)
Ordne den Graphen die entsprechende Gleichung zu.






(2 BE)
b)
Die Funktion  mit
mit  besitzt im Intervall
besitzt im Intervall  genau vier Nullstellen.
genau vier Nullstellen.
Kennzeichne diese Nullstellen näherungsweise in der Darstellung und begründe die Gültigkeit dieser Ausssage mithilfe der Darstellung.
Kennzeichne diese Nullstellen näherungsweise in der Darstellung und begründe die Gültigkeit dieser Ausssage mithilfe der Darstellung.
(3 BE)
5
Gegeben ist der Vektor  .
.
Ermittle jeweils einen Vektor , der die angegebene Bedingung erfüllt.
, der die angegebene Bedingung erfüllt.

 und
und 
Ermittle jeweils einen Vektor
a)
(1 BE)
b)
(2 BE)
c)
Der Vektor  ist senkrecht zu
ist senkrecht zu  und parallel zur
und parallel zur  -Ebene.
-Ebene.
(2 BE)
6
Ein Körper bewegt sich auf einer geradlinigen Bahn.
Der Körper wird von einer Radarstation, die mathematisch durch beschrieben wird, zuerst in
beschrieben wird, zuerst in  und fünf Sekunden später in
und fünf Sekunden später in  geortet.
geortet.
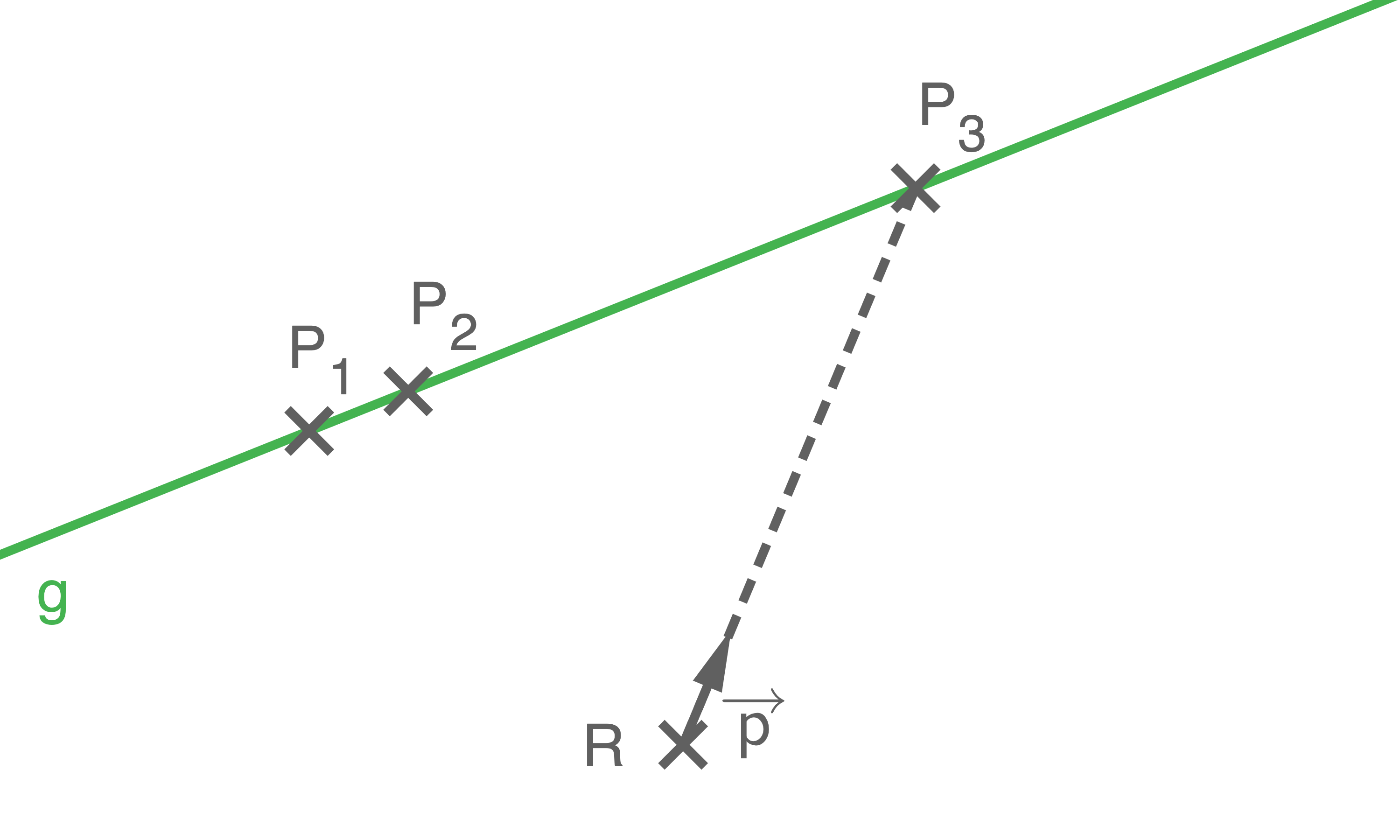
Der Körper wird von einer Radarstation, die mathematisch durch
a)
Gib eine Gleichung an, die die Flugbahn mathematisch beschreibt.
(2 BE)
b)
Der Körper wird von der Radarstation in einem weiteren Punkt  geortet.
geortet.
Die Richtung des Radarsignals wird durch mathematisch beschrieben.
mathematisch beschrieben.
Zeige, dass ist.
ist.
Die Richtung des Radarsignals wird durch
Zeige, dass

Skizze nicht maßstäblich
(3 BE)
7
Ein Glücksrad ist in genau zwei Sektoren eingeteilt, die mit den Zahlen „1“ und „2“ beschriftet sind.
Die Zahl „1“ tritt mit der Wahrscheinlichkeit von auf.
Paula und Leon vereinbaren folgendes Spiel:
auf.
Paula und Leon vereinbaren folgendes Spiel:
Die Zahl „1“ tritt mit der Wahrscheinlichkeit von
Jeder dreht das Glücksrad genau einmal.
Ist die Summe beider Zahlen ungerade, erhält Paula von Leon die Summe der Zahlen in Euro.
Ist die Summe beider Zahlen gerade, erhält Leon von Paula die Summe der Zahlen in Euro.
Ist die Summe beider Zahlen ungerade, erhält Paula von Leon die Summe der Zahlen in Euro.
Ist die Summe beider Zahlen gerade, erhält Leon von Paula die Summe der Zahlen in Euro.
a)
Bestimme die Wahrscheinlichkeit dafür, dass Paula von Leon Geld erhält.
(2 BE)
b)
Berechne den Gewinn, den Leon pro Spiel auf lange Sicht erwarten kann.
(3 BE)
8
Dargestellt sind Graphen der Dichtefunktionen von Normalverteilungen mit den Erwartungswerten  bzw.
bzw.  und den Standardabweichungen
und den Standardabweichungen  bzw.
bzw. 
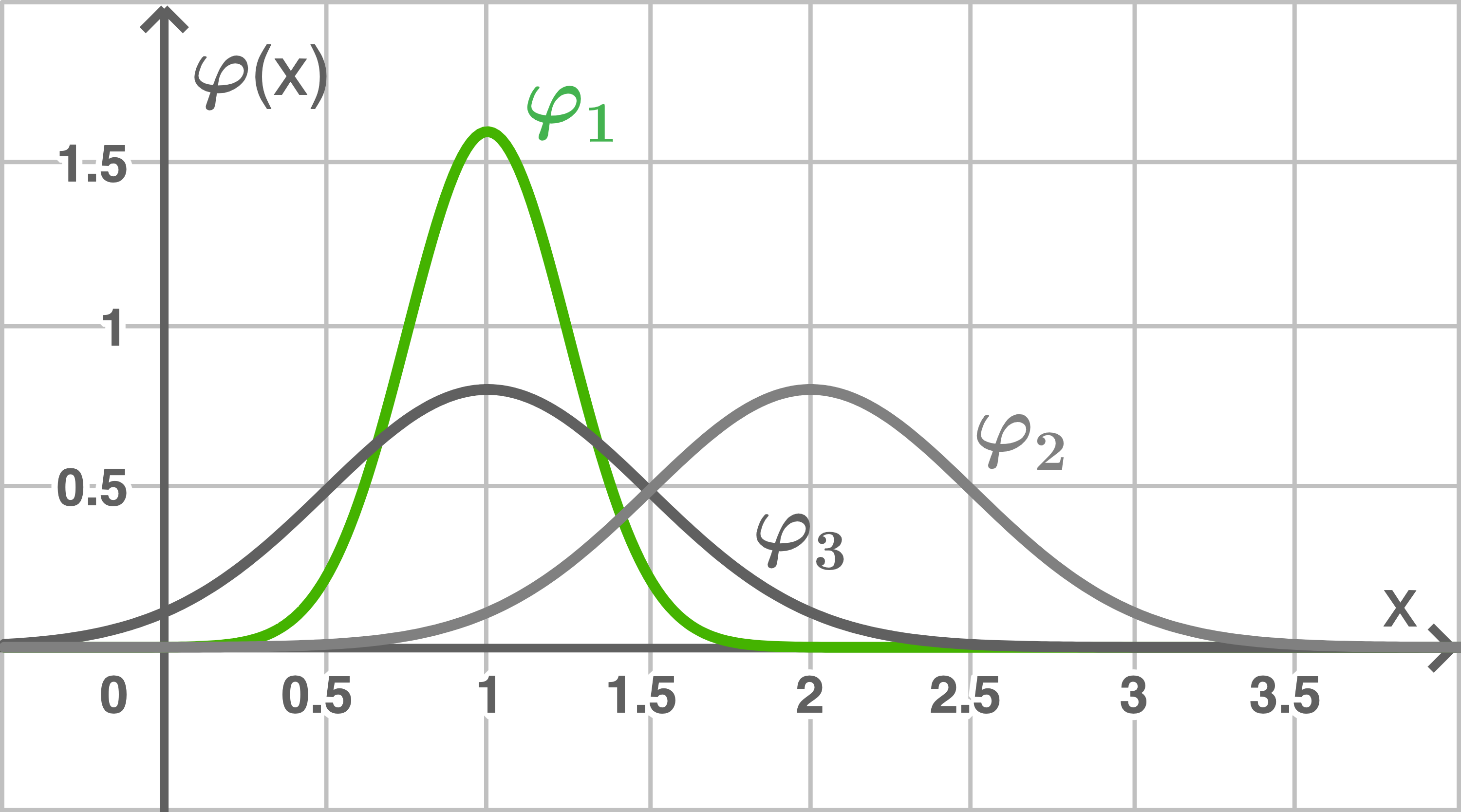

a)
Ordne den dargestellten Graphen die richtigen Werte zu.
| Graph der Funktion | |||
|---|---|---|---|
| Erwartungswert | |||
| Standardabweichung |
(2 BE)
b)
Die Zufallsgröße  ist normalverteilt und gehört zu
ist normalverteilt und gehört zu  .
.
Entscheide, ob folgende Gleichungen richtig oder falsch sind. Korrigiere gegebenenfalls.
Entscheide, ob folgende Gleichungen richtig oder falsch sind. Korrigiere gegebenenfalls.
(3 BE)
9
Gegeben ist die Koordinatengleichung einer Ebene  mit
mit  und der Punkt
und der Punkt  mit den Koordinaten
mit den Koordinaten  .
.
a)
Beschreibe die besondere Lage der Ebene  im Koordinatensystem.
im Koordinatensystem.
(1 BE)
b)
Bestimme die Koordinaten des Bildpunktes  , der bei der Spiegelung von
, der bei der Spiegelung von  an der Ebene
an der Ebene  entsteht.
entsteht.
(4 BE)
10
Ein Glücksrad mit gleichgroßen Sektoren ist einmal mit „1“ und zweimal mit „2“ und dreimal mit „3“ beschriftet.
a)
Das Glücksrad wird dreimal gedreht. Aus den angezeigten Ergebnissen werden entsprechend der Reihenfolge der Ergebnisse Zahlen gebildet.
Berechne die Wahrscheinlichkeit dafür, dass man die Zahl „321“ erhält.
Berechne die Wahrscheinlichkeit dafür, dass man die Zahl „321“ erhält.
(1 BE)
b)
Das Glücksrad wird zweimal gedreht. Aus den angezeigten Zahlen werden Summen gebildet.
Betrachtet werden folgende Ereignisse: = „Die Summe der angezeigten Zahlen ist mindestens fünf.“
= „Die Summe der angezeigten Zahlen ist mindestens fünf.“
 = „Die Summe der angezeigten Zahlen ist kleiner als fünf.“
Untersuche, ob das Ereignis
= „Die Summe der angezeigten Zahlen ist kleiner als fünf.“
Untersuche, ob das Ereignis  mit einer höheren Wahrscheinlichkeit eintritt als das Ereignis
mit einer höheren Wahrscheinlichkeit eintritt als das Ereignis  .
.
Betrachtet werden folgende Ereignisse:
(4 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
2
a)
Mit dem Satz vom Nullprodukt folgt direkt: 


b)
Eine doppelte Nullstelle ist immer eine Extremstelle. Die  Achse ist eine Tangente der Funktion
Achse ist eine Tangente der Funktion  genau dann wenn eine doppelte Nullstelle vorliegt. Das ist unter Berücksichtigung der ersten beiden Nullstellen für
genau dann wenn eine doppelte Nullstelle vorliegt. Das ist unter Berücksichtigung der ersten beiden Nullstellen für  oder
oder  der Fall. Die Aussage ist somit wahr.
der Fall. Die Aussage ist somit wahr.
3
a)
Der Graph  der Funktion
der Funktion  entsteht aus dem Graphen
entsteht aus dem Graphen  , indem dieser um
, indem dieser um  Einheiten entlang der
Einheiten entlang der  -Achse verschoben wird und um eine Einheit entlang der
-Achse verschoben wird und um eine Einheit entlang der  -Achse nach links verschoben wird.
-Achse nach links verschoben wird.
b)
4
a)
b)
Aus der Abbildung wird deutlich, dass  und
und  genau zwei gemeinsame Nullstellen, bei
genau zwei gemeinsame Nullstellen, bei  und
und  haben. An folgenden beiden Stellen gilt zudem
haben. An folgenden beiden Stellen gilt zudem 


5
a)
Lösen der gegebenen Gleichung liefert:

b)
Die Bedingung  fordert, dass ein
fordert, dass ein  existiert, welches
existiert, welches  erfüllt.
erfüllt.
Mit Hilfe der Bedingung folgt, dass
folgt, dass  sein muss, da
sein muss, da 

 und somit
und somit  Es folgt:
Es folgt:

Mit Hilfe der Bedingung
c)
Damit ein Vektor senkrecht auf einem anderen Vektor steht, muss deren Skalarprodunkt gleich  sein.
sein.
Damit ein Vektor parallel zur -Ebene ist, muss die
-Ebene ist, muss die  -Koordinate gleich
-Koordinate gleich  sein.
Da sich die ersten beiden Einträge von
sein.
Da sich die ersten beiden Einträge von  nur im Vorzeichen unterscheiden, ergibt sich
nur im Vorzeichen unterscheiden, ergibt sich  als ein möglicher Lösungsvektor.
als ein möglicher Lösungsvektor.
Damit ein Vektor parallel zur
6
a)
b)
Gerade des Radarsignals:  Schnittpunkt:
Schnittpunkt:  Aus der ersten Zeile folgt direkt
Aus der ersten Zeile folgt direkt  Einsetzen in die zweite Zeile liefert:
Einsetzen in die zweite Zeile liefert:
![\(\begin{array}[t]{rll}
3-s&=&(s-1)\cdot3 &\quad \scriptsize \mid\;+s \\[5pt]
3&=&4s-3 &\quad \scriptsize \mid\;+3 \\[5pt]
6&=&4s &\quad \scriptsize \mid\;:4 \\[5pt]
\dfrac{3}{2}&=&s
\end{array}\)](https://mathjax.schullv.de/b16c700dd5fe9ddb449e39e27119b308b23d6953dfaed1516a21b16e941f2150?color=5a5a5a) Insgesamt folgt somit:
Insgesamt folgt somit:



 Mit Hilfe der letzten Zeile folgt dann:
Mit Hilfe der letzten Zeile folgt dann:

7
a)
| Ereignis | Summe | Wahrscheinlichkeit |
|---|---|---|
| 1; 1 | 2 | |
| 1; 2 | 3 | |
| 2; 1 | 3 | |
| 2; 2 | 4 |
Paula erhält von Leon Geld
b)
8
a)
Hinweis: Bei Normalverteilungen ist der Erwartungswert der  -Wert des Hochpunktes. Die Standardabweichung kann an einer der beiden Wendestellen der Normalverteilung abgelesen werden. Es gilt, dass der Abstand des
-Wert des Hochpunktes. Die Standardabweichung kann an einer der beiden Wendestellen der Normalverteilung abgelesen werden. Es gilt, dass der Abstand des  -Wertes des Hochpunkts zu dem
-Wertes des Hochpunkts zu dem  -Wert des Wendepunktes die Standardabweichung ergibt.
-Wert des Wendepunktes die Standardabweichung ergibt.
| Graph der Funktion | |||
|---|---|---|---|
| Erwartungswert | |||
| Standardabweichung |
b)
Hinweis zur 2. Gleichung: Alternativ kann auch folgende Gleichung angegeben werden:

 Hinweis zur 3. Gleichung: Da die Zufallsgröße
Hinweis zur 3. Gleichung: Da die Zufallsgröße  normalverteilt ist, ist die Wahrscheinlichkeit für einen bestimmten Ausgang immer
normalverteilt ist, ist die Wahrscheinlichkeit für einen bestimmten Ausgang immer 
9
a)
Die Ebene ist parallel zur  -Achse, da die Variable
-Achse, da die Variable  in der Koordinatengleichung nicht vorkommt.
in der Koordinatengleichung nicht vorkommt.
b)
Aufstellen einer Hilfsgeraden: 
 Einsetzen eines allgemeinen Punktes von
Einsetzen eines allgemeinen Punktes von  in die Ebenengleichung von
in die Ebenengleichung von  liefert
liefert  und somit
und somit  Damit ist der Punkt
Damit ist der Punkt  der Schnittpunkt.
Nun können die Koordinaten von
der Schnittpunkt.
Nun können die Koordinaten von  ausgerechnet werden:
ausgerechnet werden: 
 Somit sind die Koordinaten des Spiegelpunkts
Somit sind die Koordinaten des Spiegelpunkts 
10
a)
b)
Damit die Summe der gedrehten Zahlen größer oder gleich 5 ist, können nur zwei Fälle eintreten. Entweder wird zweimal die 3 gedreht, oder es wird einmal die 3 und einmal die 2 gedreht.


 ist das Gegenereignis von
ist das Gegenereignis von  Somit gilt:
Somit gilt:
 Ereignis
Ereignis  tritt mit einer geringeren Wahrscheinlichkeit ein als Ereignis
tritt mit einer geringeren Wahrscheinlichkeit ein als Ereignis  .
.