Teil B
1
Gegeben ist die Schar der in  definierten Funktionen
definierten Funktionen  mit
mit

a)
Stelle die Funktion  in einem geeigneten Intervall graphisch dar.
in einem geeigneten Intervall graphisch dar.
Gib die Nullstelle von an.
an.
Gib die Nullstelle von
(3 BE)
b)
An den Graphen von  wird an der Stelle
wird an der Stelle  die Tangente
die Tangente  angelegt.
Weise rechnerisch nach, dass
angelegt.
Weise rechnerisch nach, dass  durch
durch  beschrieben werden kann.
beschrieben werden kann.
(2 BE)
c)
Die Funktion  ist die Stammfunktion von
ist die Stammfunktion von  deren Graph durch den Punkt
deren Graph durch den Punkt  verläuft.
Untersuche, ob das Verhältnis des Anstiegs der Stammfunktion
verläuft.
Untersuche, ob das Verhältnis des Anstiegs der Stammfunktion  an ihrer Nullstelle und des Anstieges der Tangente
an ihrer Nullstelle und des Anstieges der Tangente  mit
mit  ein ganzzahliges Vielfaches der Eulerschen Zahl
ein ganzzahliges Vielfaches der Eulerschen Zahl  ist.
ist.
(5 BE)
d)
Der Schnittpunkt des Graphen von  mit der
mit der  -Achse ist
-Achse ist  .
.
Der Schnittpunkt des Graphen von mit der
mit der  -Achse ist
-Achse ist  .
.
Für jeden Wert von schneiden sich die Graphen von
schneiden sich die Graphen von  und
und  im Punkt
im Punkt  .
Weise nach, dass die Länge der Strecke
.
Weise nach, dass die Länge der Strecke  unabhängig vom Parameter
unabhängig vom Parameter  ist.
Berechne den Wert von
ist.
Berechne den Wert von  , für den das Dreieck
, für den das Dreieck  den Flächeninhalt
den Flächeninhalt  besitzt.
besitzt.
Der Schnittpunkt des Graphen von
Für jeden Wert von
(6 BE)
e)
Für jeden Wert von  bilden der Schnittpunkt
bilden der Schnittpunkt  des Graphen von
des Graphen von  mit der
mit der  -Achse, der Extrempunkt
-Achse, der Extrempunkt  und der Wendepunkt
und der Wendepunkt  ein Dreieck.
Begründe, dass es keinen Wert für
ein Dreieck.
Begründe, dass es keinen Wert für  gibt, so dass der Winkel
gibt, so dass der Winkel  ein rechter Winkel ist.
Berechne auf zwei Dezimalen genau einen Wert von
ein rechter Winkel ist.
Berechne auf zwei Dezimalen genau einen Wert von  , für den das Dreieck rechtwinklig ist.
, für den das Dreieck rechtwinklig ist.
(6 BE)
2
Zur Simulation des kontrollierten Abflusses von großen Wassermengen durch Ventile wurde in eine Experimentieranordnung ein Durchflusssensor eingebaut. Dieser misst die momentane Durchflussgeschwindigkeit des abfließenden Wassers.
Während eines Experiments wurden folgende Werte protokolliert:
Zur mathematischen Beschreibung der Durchflussgeschwindigkeit wurde folgende Gleichung vorgeschlagen:
 Dabei wird die Zeit
Dabei wird die Zeit  in Stunden und die Durchflussgeschwindigkeit in 100 Kubikmeter pro Stunde angegeben.
in Stunden und die Durchflussgeschwindigkeit in 100 Kubikmeter pro Stunde angegeben.
 gewählt.
gewählt.
Während eines Experiments wurden folgende Werte protokolliert:
| Zeit in |
Durchflussgeschwindigkeit in |
|---|---|
a)
Bestimme für  den Wert von
den Wert von  , der eine Beschreibung für die Simulation zulässt.
, der eine Beschreibung für die Simulation zulässt.
(2 BE)
b)
Interpretiere folgende Aussagen jeweils im Sachzusammenhang.
Für weitere Untersuchungen wird
(4 BE)
c)
Berechne die Menge des abgeflossenen Wassers in Liter, wenn das Wasser restlos abgelaufen ist.
(3 BE)
d)
Das Ventil ist für eine maximale Änderung der Durchflussgeschwindigkeit von  ausgelegt.
Untersuche, ob diese Vorgabe eingehalten wird.
ausgelegt.
Untersuche, ob diese Vorgabe eingehalten wird.
(3 BE)
e)
Ein Mitarbeiter schlägt vor, zur Modellierung der Abflussgeschwindigkeit die Funktion  mit
mit  zu verwenden.
Begründe, dass diese Funktion den Sachverhalt ebenfalls näherungsweise beschreibt.
Bestimme die maximale Differenz der Durchflussgeschwindigkeit beider Modelle für
zu verwenden.
Begründe, dass diese Funktion den Sachverhalt ebenfalls näherungsweise beschreibt.
Bestimme die maximale Differenz der Durchflussgeschwindigkeit beider Modelle für 
(6 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
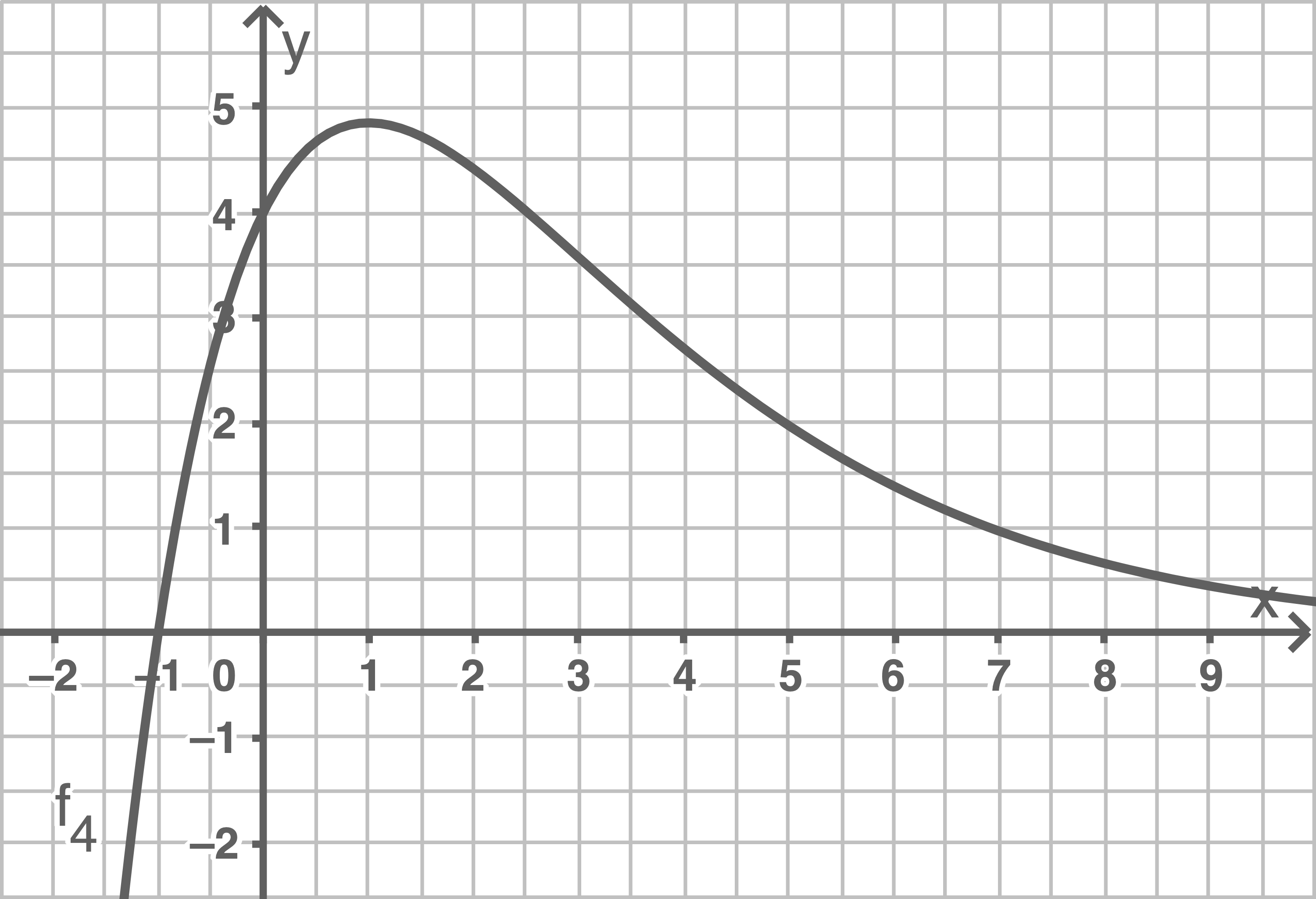
b)
Die allgemeine Tangentengleichung ist  Mit der Produktregel folgt:
Die Steigung der Tangente
Mit der Produktregel folgt:
Die Steigung der Tangente  entspricht dem Wert der Ableitungsfunktion an der Stelle
entspricht dem Wert der Ableitungsfunktion an der Stelle 
 Einsetzen in die Tangentengleichung ergibt:
Einsetzen in die Tangentengleichung ergibt:
![\(\begin{array}[t]{rll}
0&=& 4 \sqrt{\mathrm e} \cdot (-1) +b&\quad \scriptsize \mid\;+4 \sqrt{\mathrm e} \\[5pt]
4 \sqrt{\mathrm e}&=& b
\end{array}\)](https://mathjax.schullv.de/225f714a194502ca6cb0ca69505abd8725ab4bc4d370698d0f7341ee561a6009?color=5a5a5a) Somit ergibt sich:
Somit ergibt sich:
![\(\begin{array}[t]{rll}
t(x)&=& 4 \sqrt{\mathrm e} \cdot x +4 \sqrt{\mathrm e} \\[5pt]
&=&4 \sqrt{\mathrm e} \cdot (x+1)
\end{array}\)](https://mathjax.schullv.de/209fd808c93c047279fef47b63fc5df139ed802fe4134975e60fb7dd4b3a159a?color=5a5a5a)
c)
Mit dem CAS ergibt sich eine Stammfunktion zu 
 Einsetzen der Koordinaten von
Einsetzen der Koordinaten von  und lösen mit dem solve-Befehl des CAS ergibt:
und lösen mit dem solve-Befehl des CAS ergibt:
 hat eine Nullstelle bei
hat eine Nullstelle bei  Der Anstieg an dieser Stelle beträgt
Der Anstieg an dieser Stelle beträgt  Verhältnisse der Anstiege berechnen:
Verhältnisse der Anstiege berechnen:
![\(\begin{array}[t]{rll}
-8 \mathrm e^{\frac{3}{2}}\cdot v &=& 4\cdot \mathrm e^{\frac{1}{2}} &\quad \scriptsize \mid\;:\left(-8 \mathrm e^{\frac{3}{2}}\right) \\[5pt]
v&=& -2 \mathrm e
\end{array}\)](https://mathjax.schullv.de/eeb881486ac128cdb722805a97d7d72a520cfd59b848b9cbea34d18a111ccac3?color=5a5a5a)
 ist ein ganzzahliges Vielfaches von
ist ein ganzzahliges Vielfaches von 
d)
1. Schritt: Koordinaten bestimmen
Koordinaten von  bestimmen
bestimmen
![\(\begin{array}[t]{rll}
f_a(x)&=& 0 \\[5pt]
(4x+a)\cdot \mathrm e^{-\frac{1}{2}\cdot x}&=& 0 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/e589a37da02be4f7a1a3345bee90835a86575024d66cd9a33d005a1b24a3dfe3?color=5a5a5a) Mit dem Satz vom Nullprodukt und da stets
Mit dem Satz vom Nullprodukt und da stets  gilt, folgt
gilt, folgt  und daraus
und daraus  als Nullstelle.
Die Koordinaten von
als Nullstelle.
Die Koordinaten von  ergeben sich also durch
ergeben sich also durch  Koordinaten von
Koordinaten von  bestimmen
bestimmen
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/2734efeeb267a881243582104b5ee0497a5b78977eec0e863b934e774605bfb9?color=5a5a5a) Mit dem Satz vom Nullprodukt und da stets
Mit dem Satz vom Nullprodukt und da stets  gilt, folgt:
gilt, folgt:
![\(\begin{array}[t]{rll}
4-2x-\dfrac{a}{2} &=& 0 &\quad \scriptsize \mid\;-4 \\[5pt]
-2x-\dfrac{a}{2}&=& -4 &\quad \scriptsize \mid\;:(-2) \\[5pt]
x+\dfrac{a}{4}&=& 2 &\quad \scriptsize \mid\;-\dfrac{a}{4} \\[5pt]
x&=& 2-\dfrac{a}{4}
\end{array}\)](https://mathjax.schullv.de/87fc935e3bdb0c357e6b8cc9b693f2b6b6e4a8ebe0438257c6f5f4355d3f4bf7?color=5a5a5a) Die Koordinaten von
Die Koordinaten von  ergeben sich also durch
ergeben sich also durch  Koordinaten von
Koordinaten von  bestimmen
bestimmen
![\(\begin{array}[t]{rll}
f_a(x)&=& f](https://mathjax.schullv.de/9d3f135b9ff10e115e25e9ab33eb9d96f02b8e58aa51c5476952f65d8bf3eaeb?color=5a5a5a) Die Koordinaten von
Die Koordinaten von  sind gegeben durch
sind gegeben durch  2. Schritt: Länge der Strecke berechnen
2. Schritt: Länge der Strecke berechnen
 Somit ist die Strecke
Somit ist die Strecke  unabhängig vom Parameter
unabhängig vom Parameter  3. Schritt: Wert von
3. Schritt: Wert von  berechnen
berechnen
 bildet die Basis des Dreiecks
bildet die Basis des Dreiecks 
 Die Höhe
Die Höhe  des Dreicks ergibt sich mit der
des Dreicks ergibt sich mit der  -Koordinate von
-Koordinate von  zu
zu  Der Flächeninhalt des Dreiecks folgt mit
Der Flächeninhalt des Dreiecks folgt mit  Es soll
Es soll  gelten. Durch Gleichsetzen und Einsetzen folgt:
gelten. Durch Gleichsetzen und Einsetzen folgt:
![\(\begin{array}[t]{rll}
\dfrac{8}{3}&=& \dfrac{1}{2}\cdot b\cdot h \\[5pt]
\dfrac{8}{3} &=& \dfrac{1}{2}\cdot 2\cdot \dfrac{8}{3}\cdot \mathrm e^{\frac{a}{8}-\frac{1}{3}} &\quad \scriptsize \mid\;\cdot \dfrac{3}{8} \\[5pt]
1&=& \mathrm e^{\frac{a}{8}-\frac{1}{3}} &\quad \scriptsize \mid\; \ln() \\[5pt]
0&=& \dfrac{a}{8}-\dfrac{1}{3} &\quad \scriptsize \mid\; +\dfrac{1}{3} \;\mid\; \cdot 8 \\[5pt]
\dfrac{8}{3}&=& a
\end{array}\)](https://mathjax.schullv.de/50f45d0b24575596fa049dc6fc8d34798c572ec6de341c0870145a21e84a540a?color=5a5a5a)
e)
Mit dem Skalarprodukt des CAS folgt  Ein rechter Winkel im Dreieck ergibt sich für
Ein rechter Winkel im Dreieck ergibt sich für  (oder
(oder  ).
).
2
a)
b)
Aussage  Die Durchflussgeschwindigkeit nimmt nach 4,5 Stunden ab.
Aussage
Die Durchflussgeschwindigkeit nimmt nach 4,5 Stunden ab.
Aussage  Zwischen der vierten und der fünften Stunde fließen
Zwischen der vierten und der fünften Stunde fließen  ab.
ab.
c)
d)
Die maximale Änderung der Durchflussgeschwindigkeit entspricht dem Wert der Wendestelle.
Mit dem CAS ergibt sich die Wendestelle zu  Mit
Mit  wird die Vorgabe eingehalten.
wird die Vorgabe eingehalten.
e)
| 1 | 7,29 |
| 2 | 5,89 |
| 4 | 3,25 |
| 6 | 1,58 |
| 8 | 0,74 |
| 0,28 | 0,14 |