Teil C1
1
Von einer geraden quadratischen Pyramide 
sind die Punkte 
und 
gegeben.
ist eine Gerade 
gegeben durch 
a)
Gib die Koordinaten des Punkts 
an.
Stelle die Pyramide in einem Koordinatensystem graphisch dar.
Stelle die Pyramide in einem Koordinatensystem graphisch dar.
(3 BE)
b)
Gib die Höhe der Pyramide an.
Berechne die Länge der Seitenkante
Für jede reelle Zahl Berechne die Länge der Seitenkante
(3 BE)
c)
Für 
und 
wird eine Punktmenge bestimmt.
Beschreibe die Lage dieser Punktmenge bezogen auf die Pyramide
Beschreibe die Lage dieser Punktmenge bezogen auf die Pyramide
(2 BE)
d)
Unter den Geraden gibt es Geraden, die mit der Gerade 
einen Winkel von 
einschließen.
Berechne die Werte für
Berechne die Werte für
(3 BE)
e)
Alle Geraden liegen in einer Ebene 
, die die Punkte 
und 
enthält.
Bestimme eine Gleichung für in Koordinatenform.
(Zur Kontrolle:
)
Bestimme eine Gleichung für
(Zur Kontrolle:
(3 BE)
f)
Berechne den Abstand des Punktes 
von der Ebene 
(3 BE)
g)
Gegeben ist die Gerade 
durch 
Zeige, dass die Gerade in der Ebene liegt, aber nicht zu den Geraden gehört.
(3 BE)
h)
Zu jeder Koordinatenebene gibt es eine parallele Ebene, die das Volumen der Pyramide halbiert.
Ermittle jeweils eine Gleichung dieser Ebenen.
Ermittle jeweils eine Gleichung dieser Ebenen.
(5 BE)
2
Zur Verkehrsunfallstatistik im Jahr 2014 für die Stadt Jena wurde veröffentlicht:
„[...] Allerdings gibt es bei den Fahranfängern eine positive Tendenz. Ihr Anteil an den Unfällen liegt bei 8 Prozent und damit [...] niedriger als ein Jahr zuvor. Ältere Fahrer über 65 Jahren verursachen dagegen 14 Prozent aller Unfälle [...].“
(Nach: https://www.otz.de/leben/vermischtes/auto-verkehr/traurige-bilanz-des-jahres-2014-hoechste-unfallzahlen-in-jena-seit-10-jahren-id220905863.html (14./15.05.2015) Man geht davon aus, dass diese Anteile sich in den folgenden Jahren nicht ändern werden.
Verwende zur Lösung aller Aufgaben das Modell der Binomialverteilung.
für Unfälle, die von Fahranfängern in Jena verursacht werden, auf Thüringen übertragbar ist. Dazu sollen die nächsten 100 Unfälle ausgewertet werden. Werden von diesen 100 Unfällen 3 bis 13 Unfälle von Fahranfängern verursacht, so will man glauben, dass auch in Thüringen der Unfälle von Fahranfängern verursacht werden.
(Nach: https://www.otz.de/leben/vermischtes/auto-verkehr/traurige-bilanz-des-jahres-2014-hoechste-unfallzahlen-in-jena-seit-10-jahren-id220905863.html (14./15.05.2015) Man geht davon aus, dass diese Anteile sich in den folgenden Jahren nicht ändern werden.
Verwende zur Lösung aller Aufgaben das Modell der Binomialverteilung.
a)
Berechne unter Verwendung der Zahlen für das Jahr 2014 folgende Wahrscheinlichkeiten für 2017:
„Höchstens zwei der nächsten 20 Unfälle im Stadtgebiet werden von Fahranfängern verursacht.“
„Mehr als zwei der nächsten 20 Unfälle im Stadtgebiet werden von Fahrern über 65 Jahren verursacht.“
(4 BE)
b)
Betrachtet werden die nächsten 250 Unfälle.
Ermittle das Intervall symmetrisch um den Erwartungswert, in dem etwa
der von Fahranfängern verursachten Unfälle liegen.
Mit einem Signifikanztest soll untersucht werden, ob der Wert von Ermittle das Intervall symmetrisch um den Erwartungswert, in dem etwa
(4 BE)
c)
Ermittle hierfür die Größe des 
-Fehlers (Fehler 1. Art) dieses Tests.
(3 BE)
d)
Erläutere die Bedeutung des -Fehlers in diesem Zusammenhang.
(2 BE)
e)
Es wurden fünf Fahranfänger als Unfallverursacher unter den nächsten 
Unfällen gezählt.
Beurteile hierzu den Wahrheitsgehalt der Aussage: „Auch in Thüringen werden der Unfälle von Fahranfängern verursacht.“
Beurteile hierzu den Wahrheitsgehalt der Aussage: „Auch in Thüringen werden
(2 BE)
1.
a)
Koordinaten angeben
Damit sich eine quadratische Pyramide ergibt, muss der Punkt die Koordinaten 
besitzen.
Pyramide im Koordinatensystem einzeichnen
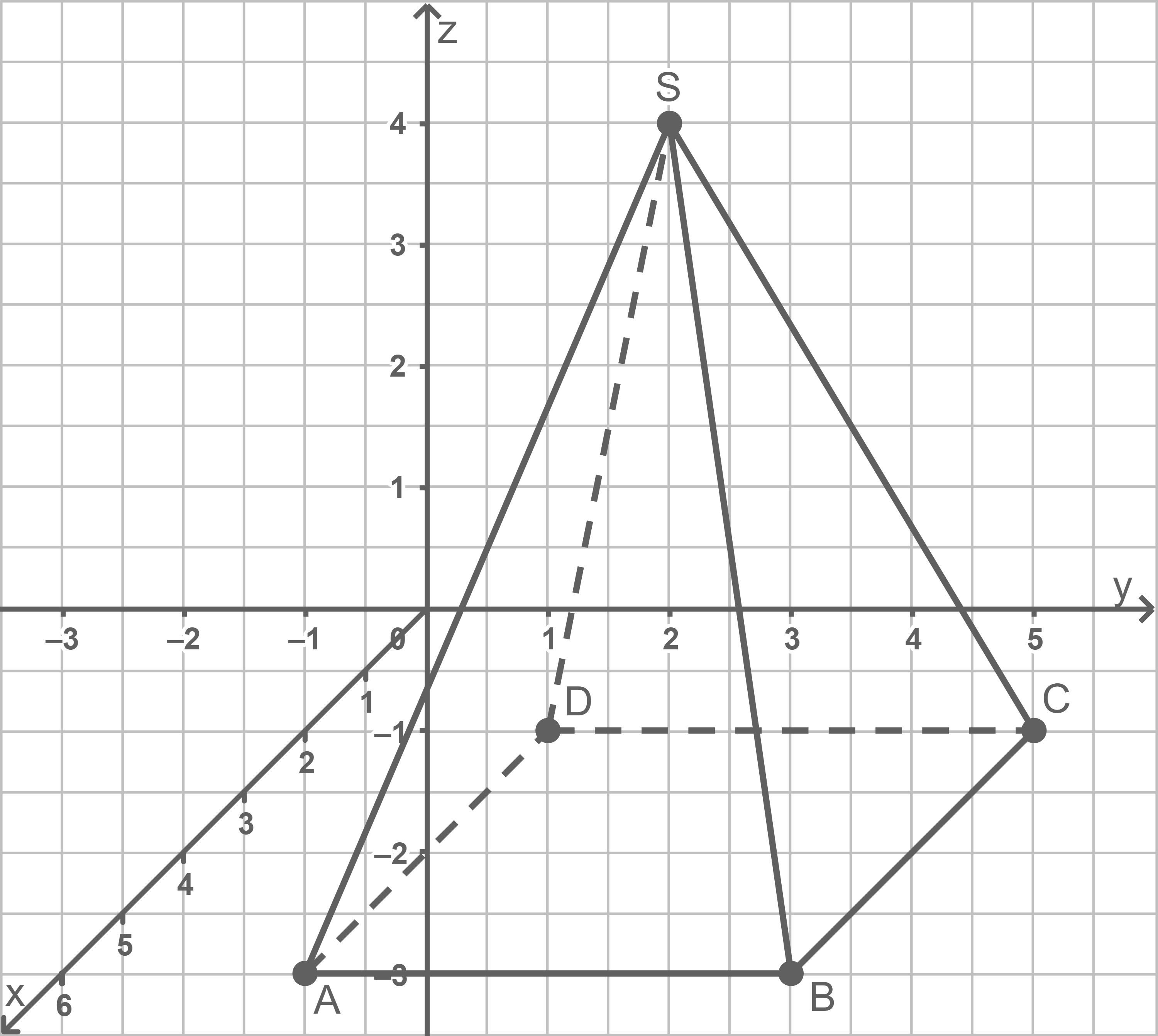
b)
Höhe der Pyramide angeben
Die Grundfläche der Pyramide liegt in der 
-Ebene. Die Höhe wird deshalb durch die 
-Koordinate der Spitze beschriebenund beträgt somit 
Länge der Seitenkante bestimmen
![\(\begin{array}[t]{rll}
\left|\overrightarrow{AS}\right|&=&\left|\pmatrix{4\\4\\6}-\pmatrix{6\\2\\0}\right|& \\[5pt]
&=&\left|\pmatrix{-2\\2\\6}\right|& \\[5pt]
&=&2\sqrt{11}& \\[5pt]
\end{array}\)](https://mathjax.schullv.de/3b42eeb6276c544f7b0688337f1363d90fa79cfece41d5fe94de2c84bd7ccf05?color=5a5a5a)
Die Strecke 
hat eine Länge von 
c)
Die Punktmenge ist eine Strecke, die für 
durch folgende Gleichung beschrieben wird:
Einsetzen von 
liefert den einen Endpunkt:
Für den anderen Endpunkt folgt durch Einsetzen von 
Der Ortsvektor 
stimmt mit 
überein, das heißt der andere Endpunkt ist der Mittelpunkt der Strecke 
Die Punktmenge ist somit die Strecke, die die Pyramidenseite 
vertikal mittig teilt.
d)
Die Formel für den Schnittwinkel zweier Geraden liefert mit Hilfe des solve-Befehls des CAS:
Die Werte von 
für die die Geraden die Gerade unter einem Winkel von schneiden betragen 
e)
Ein Normalenvektor der Ebene ergibt sich mit Hilfe des CAS mit dem Kreuzprodukt zweier beliebiger Spannvektoren der Ebene:
![\(\begin{array}[t]{rll}
\overrightarrow{n}&=& \overrightarrow{SC}\times \overrightarrow{SD} \\[5pt]
&=& \pmatrix{-2\\2\\-6} \times \pmatrix{-2\\-2\\-6} \\[5pt]
&=& \pmatrix{-24 \\ 0 \\ 8}\\[5pt]
\end{array}\)](https://mathjax.schullv.de/bb6f87561d93a2aaac71105b42dc0f33671764309609350a21935692ae33f899?color=5a5a5a)
Mit dem skalierten Normalenvektor 
wird eine vorläufige Gleichung von in Koordinatenform erhalten:
Einsetzen der Koordinaten von beispielsweise liefert für 
![\(\begin{array}[t]{rll}
-3\cdot 4+6&=&d \\[5pt]
-6&=& d
\end{array}\)](https://mathjax.schullv.de/afa935494259687ac9330f3a0dd7c6750eb8d776ec0c076028968a0954d8ea4d?color=5a5a5a)
Eine Gleichung von in Koordinatenform lautet somit:
f)
Für die Hessesche Normalenform der Ebene ergibt sich:
![\(\begin{array}[t]{rll}
0&=&\dfrac{-3x+z+6}{\sqrt{(-3)^2+0^2+1^2}} \\[5pt]
&=&\dfrac{-3x+z+6}{\sqrt{10}}
\end{array}\)](https://mathjax.schullv.de/60b19f03415acd980c7ce24651406a5ea37a445904b7b7315354d5c716d8f333?color=5a5a5a)
Für den Abstand des Punktes zur Ebene folgt somit:
g)
Einsetzen eines allgemeinen Punktes 
der Geraden in die Ebenengleichung von liefert:
![\(\begin{array}[t]{rll}
-3\cdot4+6&=&-6 \\[5pt]
-6&=&-6
\end{array}\)](https://mathjax.schullv.de/596a672598f7fb8c9b24e7d256c319a3c106228778af67572b19fc806f985a67?color=5a5a5a)
Somit liegt die Gerade in der Ebene . Die Geraden und besitzen den gleichen Stützvektor. Um zur Geradenschar zu gehören, muss der Richtungsvektor von somit linear abhängig von dem Richtungsvektor von sein:
Die erste und dritte Zeile liefern 
Aus der zweiten Zeile folgt jedoch 
somit kann kein solches 
existieren und die Gerade gehört nicht zu den Geraden 
h)
Gleichung der zur -Ebene parallelen Ebene ermitteln
Die zur -Ebene parallele Ebene schneidet die Pyramide in einer bestimmten Höhe und zerteilt sie in einen Pyramidenstumpf 
und eine weitere, kleinere Pyramide 
die zur großen Pyramide ähnlich ist:
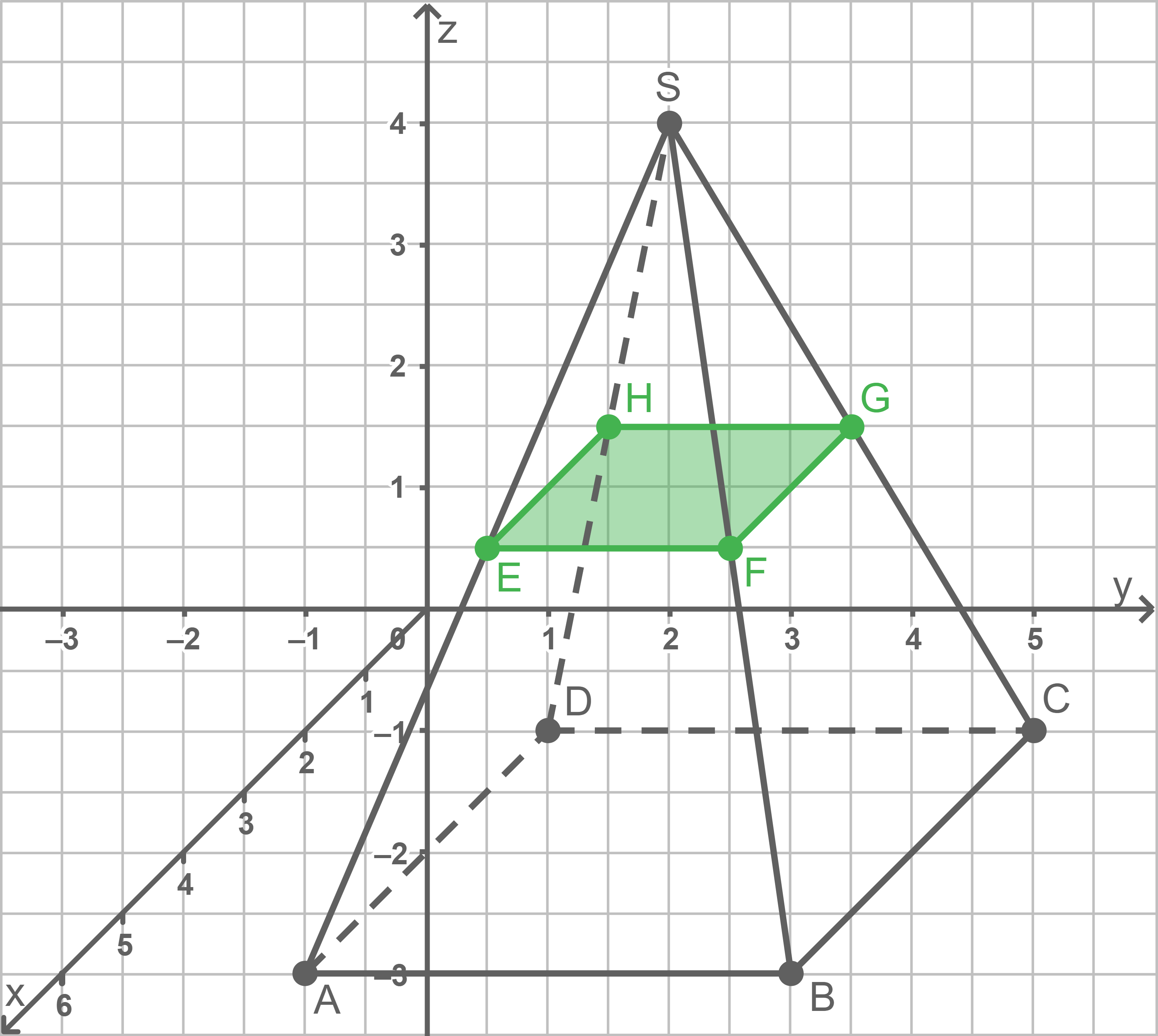Für den Längenfaktor der ähnlichen Pyramiden gilt also, dass die Streckenlängen der Bildfigur das -fache der Streckenlängen der Originalfigur betragen, sowie das Volumen der Bildfigur das 
-fache des Volumens der Originalfigur beträgt. Da die gesuchte Ebene die Pyramide in zwei volumengleiche Teile unterteilen soll, gilt 
und damit ![\(k=\sqrt[3]{\frac{1}{2}}.\)](https://mathjax.schullv.de/888db91047c6d856a3f83f747436129d78873fc27ae0629d6c68b3349f609ed8?color=5a5a5a)
Mit der Höhe
der großen Pyramide folgt somit für die Höhe 
der kleinen Pyramide:
![\(h_k = k\cdot h = \sqrt[3]{\frac{1}{2}}\cdot 6\)](https://mathjax.schullv.de/0642c1be027cc5de51eb94ea1747154694bf39661309f904d7dd1daf37bc9b5a?color=5a5a5a)
Die Grundfläche der kleinen Pyramide liegt in der Ebene, die die große Pyramide in zwei gleichgroße Teile teilt. Für die Höhe dieser Ebene gilt:
![\(z=6-\sqrt[3]{\frac{1}{2}}\cdot 6 = 6-3\sqrt[3]{4}\)](https://mathjax.schullv.de/baf14e1bde1bb3cd841c004efffa7a0c863acce3e17dd986f835744cf06d9174?color=5a5a5a)
Eine Ebenengleichung der gesuchten Ebene lautet somit ![\(z=6-3\sqrt[3]{4}.\)](https://mathjax.schullv.de/15e431745895a1dd187bd19c33a4986ae7fb21046e244952c5e33aba49f7fd72?color=5a5a5a)
Gleichung der zur 
-Ebene parallelen Ebene ermitteln
Da die Pyramide gerade ist, verläuft die zur -Ebene parallele Ebene, die das Volumen der Pyramide halbiert, durch die Spitze 
Der Abstand von zur -Ebene ist durch die 
-Koordinate 
des Punktes gegeben, somit hat die gesuchte Ebene die Gleichung 
Gleichung der zur 
-Ebene parallelen Ebene ermitteln
Mit gleicher Argumentation wie im Fall der -Ebene, ergibt sich die Ebenengleichung hier mit Hilfe der 
-Koordinate 
der Pyramidenspitze. Die gesuchte Ebene ist somit durch die Gleichung 
gegeben.
Mit der Höhe
2.
a)
Wahrscheinlichkeit für Ereignis 
berechnen
Die Zufallsgröße 
gibt die zufällige Anzahl der Unfälle im Stadtgebiet, die von Fahranfängern verursacht werden an und ist binomialverteilt mit 
und 
Mit dem CAS folgt:
![\(\begin{array}[t]{rll}
P(A)&=&B_{20;0,08}(X\leq 2) \\[5pt]
&\approx&0,7879\\[5pt]
&=&78,79\,\%
\end{array}\)](https://mathjax.schullv.de/2a5e9715e45fc1b16b411c36a162554d1b160647c0cac87e611a9233084eca3b?color=5a5a5a)
Wahrscheinlichkeit für Ereignis 
berechnen
Die Zufallsgröße 
gibt die zufällige Anzahl der Unfälle im Stadtgebiet, die von Fahrern über 
Jahren verursacht werden an, und ist binomialverteilt mit und 
Mit dem CAS folgt:
![\(\begin{array}[t]{rll}
P(B)&=&B_{20;0,8}(3 \leq Y \leq 20) \\[5pt]
&\approx&0,545\\[5pt]
&=& 54,5\,\%
\end{array}\)](https://mathjax.schullv.de/2140b018208aebf328f4c0f021a8f2e03ed25fdaddcf175a2e4f900dea09925d?color=5a5a5a)
b)
Die Zufallsvariable 
beschreibt die zufällige Anzahl der von Fahranfängern verursachten Unfällen und ist binomialverteilt mit 
und Für den Erwartungswert von folgt 
Gesucht ist ein Intervall ![\([\mu-k;\mu+k],\)](https://mathjax.schullv.de/bd36f5828421894ab29371ba59a3065cfe62843fb57118ef95c4b77f3f69cddb?color=5a5a5a)
sodass gilt:
Systematisches Ausprobieren mit dem CAS liefert:
Das gesuchte Intervall um den Erwartungswert ist ![\([15;20].\)](https://mathjax.schullv.de/becb450ca32522afa44d16a5d7cb6198ee34f2fadb3d35fae8388ed25ea59650?color=5a5a5a)
c)
Der Fehler 1. Art entspricht der Wahrscheinlichkeit, die Nullhypothese fälschlicherweise abzulehnen. Die Zufallsvariable 
beschreibt die Anzahl der von Fahranfängern verursachten Unfällen und ist binomialverteilt mit 
und Mit dem CAS folgt somit für den Fehler 1. Art:
d)
Der Fehler 
Art beschreibt die Wahrscheinlichkeit, dass die Nullhypothese fälschlicherweise abgelehnt wird. Das bedeutet, dass davon ausgegangen wird, dass in Thüringen mehr oder weniger als 
aller Unfälle von Fahranfängern verursacht werden, obwohl die tatsächliche Quote genau bei liegt.
e)
Der Annahmebereich des Hypothesentestes ist ![\(A[3;13].\)](https://mathjax.schullv.de/31cc64a8f265e3c08c68e39442216b02dd4635a80cf6036078eea945793164af?color=5a5a5a)
Somit liegen die 
von Fahranfängern verursachten Unfälle, im Annahmebereich und die Hypothese kann nicht verworfen werden. Allerdings besteht eine Restwahrscheinlichkeit, dass die Hypothese doch nicht zuftrifft, der Fehler 2. Art.
1.
a)
Koordinaten angeben
Damit sich eine quadratische Pyramide ergibt, muss der Punkt die Koordinaten besitzen.
Pyramide im Koordinatensystem einzeichnen
b)
Höhe der Pyramide angeben
Die Grundfläche der Pyramide liegt in der -Ebene. Die Höhe wird deshalb durch die -Koordinate der Spitze beschriebenund beträgt somit
Länge der Seitenkante bestimmen
Die Strecke hat eine Länge von
c)
Die Punktmenge ist eine Strecke, die für durch folgende Gleichung beschrieben wird:
Einsetzen von liefert den einen Endpunkt:
Für den anderen Endpunkt folgt durch Einsetzen von
Der Ortsvektor stimmt mit überein, das heißt der andere Endpunkt ist der Mittelpunkt der Strecke Die Punktmenge ist somit die Strecke, die die Pyramidenseite vertikal mittig teilt.
d)
Die Formel für den Schnittwinkel zweier Geraden liefert mit Hilfe des solve-Befehls des CAS:
Die Werte von für die die Geraden die Gerade unter einem Winkel von schneiden betragen
e)
Ein Normalenvektor der Ebene ergibt sich mit Hilfe des CAS mit dem Kreuzprodukt zweier beliebiger Spannvektoren der Ebene:
Mit dem skalierten Normalenvektor wird eine vorläufige Gleichung von in Koordinatenform erhalten:
Einsetzen der Koordinaten von beispielsweise liefert für
Eine Gleichung von in Koordinatenform lautet somit:
f)
Für die Hessesche Normalenform der Ebene ergibt sich:
Für den Abstand des Punktes zur Ebene folgt somit:
g)
Einsetzen eines allgemeinen Punktes der Geraden in die Ebenengleichung von liefert:
Somit liegt die Gerade in der Ebene . Die Geraden und besitzen den gleichen Stützvektor. Um zur Geradenschar zu gehören, muss der Richtungsvektor von somit linear abhängig von dem Richtungsvektor von sein:
Die erste und dritte Zeile liefern Aus der zweiten Zeile folgt jedoch somit kann kein solches existieren und die Gerade gehört nicht zu den Geraden
h)
Gleichung der zur -Ebene parallelen Ebene ermitteln
Die zur -Ebene parallele Ebene schneidet die Pyramide in einer bestimmten Höhe und zerteilt sie in einen Pyramidenstumpf und eine weitere, kleinere Pyramide die zur großen Pyramide ähnlich ist:
Für den Längenfaktor der ähnlichen Pyramiden gilt also, dass die Streckenlängen der Bildfigur das -fache der Streckenlängen der Originalfigur betragen, sowie das Volumen der Bildfigur das -fache des Volumens der Originalfigur beträgt. Da die gesuchte Ebene die Pyramide in zwei volumengleiche Teile unterteilen soll, gilt und damit
Mit der Höhe der großen Pyramide folgt somit für die Höhe der kleinen Pyramide:
Die Grundfläche der kleinen Pyramide liegt in der Ebene, die die große Pyramide in zwei gleichgroße Teile teilt. Für die Höhe dieser Ebene gilt:
Eine Ebenengleichung der gesuchten Ebene lautet somit
Gleichung der zur -Ebene parallelen Ebene ermitteln
Da die Pyramide gerade ist, verläuft die zur -Ebene parallele Ebene, die das Volumen der Pyramide halbiert, durch die Spitze Der Abstand von zur -Ebene ist durch die -Koordinate des Punktes gegeben, somit hat die gesuchte Ebene die Gleichung
Gleichung der zur -Ebene parallelen Ebene ermitteln
Mit gleicher Argumentation wie im Fall der -Ebene, ergibt sich die Ebenengleichung hier mit Hilfe der -Koordinate der Pyramidenspitze. Die gesuchte Ebene ist somit durch die Gleichung gegeben.
Mit der Höhe
2.
a)
Wahrscheinlichkeit für Ereignis berechnen
Die Zufallsgröße gibt die zufällige Anzahl der Unfälle im Stadtgebiet, die von Fahranfängern verursacht werden an und ist binomialverteilt mit und Mit dem CAS folgt:
Wahrscheinlichkeit für Ereignis berechnen
Die Zufallsgröße gibt die zufällige Anzahl der Unfälle im Stadtgebiet, die von Fahrern über Jahren verursacht werden an, und ist binomialverteilt mit und Mit dem CAS folgt:
b)
Die Zufallsvariable beschreibt die zufällige Anzahl der von Fahranfängern verursachten Unfällen und ist binomialverteilt mit und Für den Erwartungswert von folgt Gesucht ist ein Intervall sodass gilt:
Systematisches Ausprobieren mit dem CAS liefert:
Das gesuchte Intervall um den Erwartungswert ist
c)
Der Fehler 1. Art entspricht der Wahrscheinlichkeit, die Nullhypothese fälschlicherweise abzulehnen. Die Zufallsvariable beschreibt die Anzahl der von Fahranfängern verursachten Unfällen und ist binomialverteilt mit und Mit dem CAS folgt somit für den Fehler 1. Art:
d)
Der Fehler Art beschreibt die Wahrscheinlichkeit, dass die Nullhypothese fälschlicherweise abgelehnt wird. Das bedeutet, dass davon ausgegangen wird, dass in Thüringen mehr oder weniger als aller Unfälle von Fahranfängern verursacht werden, obwohl die tatsächliche Quote genau bei liegt.
e)
Der Annahmebereich des Hypothesentestes ist Somit liegen die von Fahranfängern verursachten Unfälle, im Annahmebereich und die Hypothese kann nicht verworfen werden. Allerdings besteht eine Restwahrscheinlichkeit, dass die Hypothese doch nicht zuftrifft, der Fehler 2. Art.