Teil C1

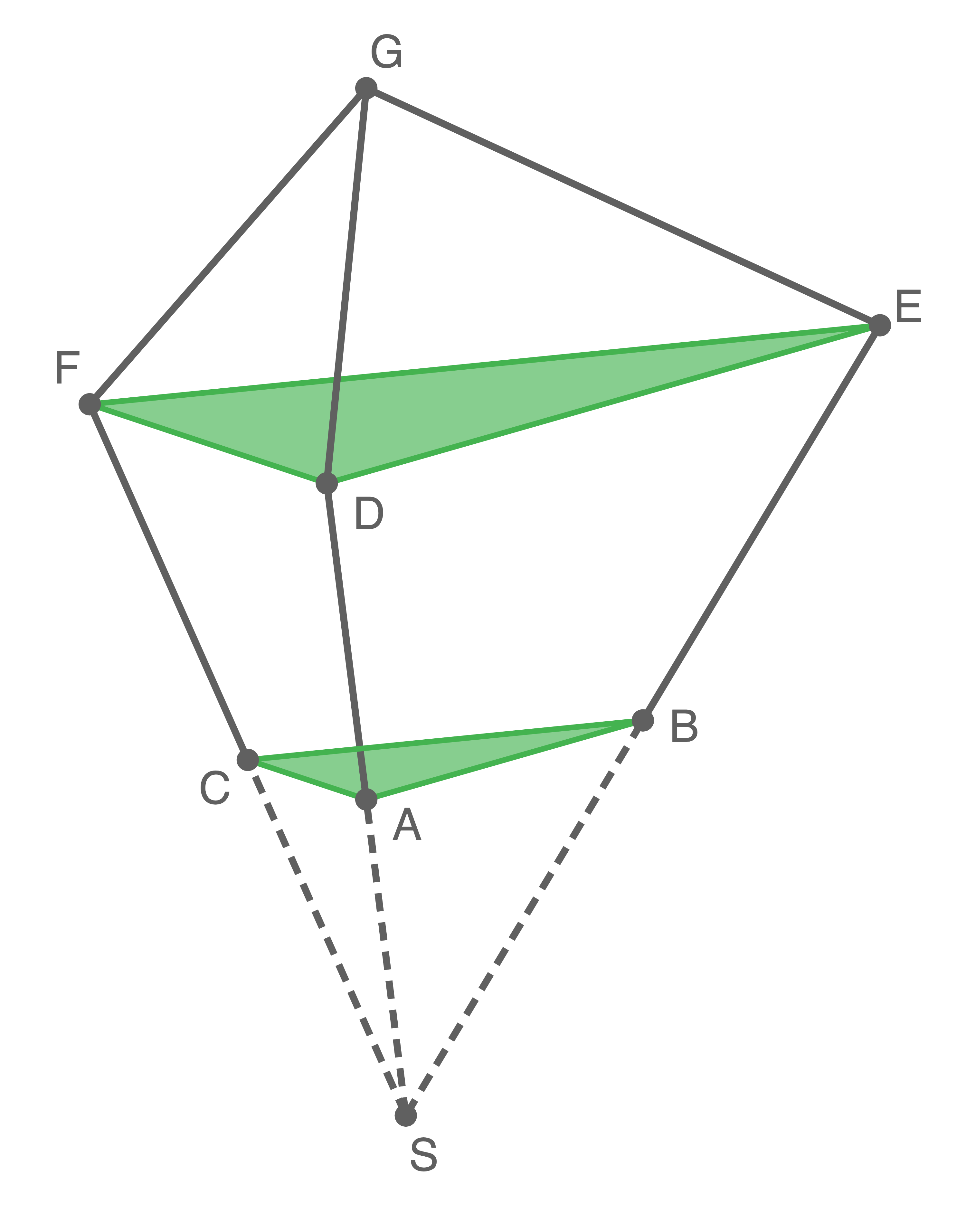
Das Gebäude eines Museums kann modellhaft durch den abgebildeten Körper $ABCDEFG$ dargestellt werden. Die obere Etage des Museums entspricht dabei der Pyramide $DEFG,$ die untere Etage dem Körper $ABCDEF,$ der Teil der Pyramide $DEFS$ ist.
Die Ebene, in der das Dreieck $ABC$ liegt, beschreibt die Horizontale. Das Dreieck $DEF$ liegt parallel zu dieser Ebene.
In einem kartesischen Koordinatensystem gilt für die Lage einiger der genannten Punkte:

$A(-5\mid 5\mid 0),$ $B(-5\mid 25\mid 0),$ $D(0\mid 0\mid 15),$ $E(0\mid 30\mid 15),$ $F(-25\mid 5\mid 15)$ und $G(-10\mid 10\mid 35).$

Eine Längeneinheit im Koordinatensystem entspricht $1\,\text{m}$ in der Realität.

thüringen mathe abi 2018 teil c1 abbildung 1

Die folgenden Rechnungen zeigen ein mögliches Vorgehen zur Ermittlung der Koordinaten von $S:$

Rechnung anzeigen

d.h. $S(-15\mid 15\mid -30)$

Erläutere das dargestellte Vorgehen.

(4 BE)

Weise nach, dass die Bodenfläche der oberen Etage nicht rechtwinklig ist.

(3 BE)

Berechne für das Dreieck $DEF$ die Größe des Innenwinkels bei $E$ sowie die Länge der Höhe $h$ zur Seite $\overline{EF}.$

(4 BE)

Für die obere Etage wird eine Anlage zur Entfeuchtung der Luft installiert, die für $100\,\text{m}^3$ Rauminhalt eine elektrische Leistung von $0,8$ Kilowatt benötigt.
Weise nach, dass für den Betrieb der Anlage eine Leistung von $25$ Kilowatt ausreichend ist.

(4 BE)

Weise nach, dass die Gerade $AG$ und die Ebene, in der das Dreieck $DEF$ liegt, sich im Punkt $R\left(-\dfrac{50}{7}\mid \dfrac{50}{7}\mid 15\right)$ schneiden.

(3 BE)

An einer Metallstange, die durch die Strecke $\overline{RG}$ dargestellt wird, ist ein Scheinwerfer befestigt, dessen Größe vernachlässigt werden soll. Der Scheinwerfer beleuchtet aus einer Entfernung von $5\,\text{m}$ diejenige Wand, die im Modell durch das Dreieck $EFG$ dargestellt wird.
Berechne die Koordinaten des Punktes, der die Position des Scheinwerfers im Modell beschreibt.

(7 BE)

Fairer Handel wird in einer globalisierten Welt immer wichtiger. Der Umsatz der Produkte mit Fairtrade-Siegel nimmt seit 1993 stetig zu. Im Jahr 2015 wurden in Deutschland $978$ Millionen Euro mit Produkte dieses Siegels umgesetzt.
Der Anteil am Gesamtumsatz von Produkten mit Fairtrade-Siegel des Jahres 2015 ist im Kreisdiagramm dargestellt.

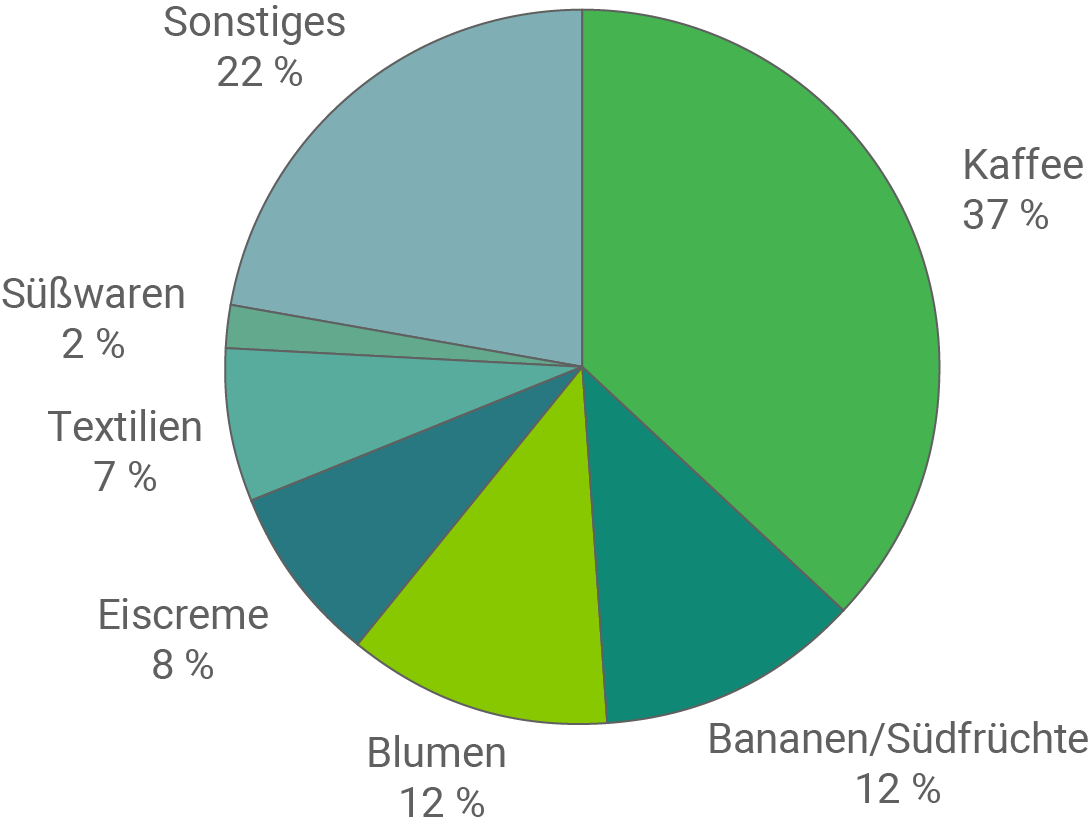
thüringen mathe abi 2018 teil c1 abbildung 2

Berechne den „Umsatz an Kaffee“ sowie den „Umsatz an Süßwaren und Eiscreme“ in Euro für 2015 in Deutschland.

(2 BE)

Der Inhaber eines Eine-Welt-Ladens möchte sein Sortiment den aktuellen Kundenwünschen anpassen und beobachtet das Kaufverhalten seiner Kunden. Er geht zunächst davon aus, dass sich die Anteile der umsatzstärksten Produkte auf die Anteile der Käufer der jeweiligen Produkte übertragen lassen.

Nutze die Grafik und berechne die Wahrscheinlichkeit folgender Ereignisse unter Annahme des Modells der Binomialverteilung:

$A:\,=$

„Mindestens $40$ der nächsten $150$ Kunden kaufen Kaffee.“

$B:\,=$

„Mehr als ein Zehntel der nächsten $150$ Kunden kaufen Textilien.“

(4 BE)

Beschreibe unter Verwendung der Grafik ein Ereignis $C,$ dessen Wahrscheinlichkeit durch den Term:

$P(C)= 1-(10\cdot 0,07^1\cdot 0,93^9+0,93^{10})$

berechnet werden kann.

(3 BE)

Der Inhaber zählt unter den $150$ Kunden $75$ Kaffeekäufer und vermutet, dass die Hälfte seiner Kunden Kaffee kauft. Dies soll mittels eines zweiseitigen Signifikanztests untersucht werden. Dazu wird das Kaufverhalten der nächsten $200$ Kunden beobachtet.

Beschreibe die Bedeutung des $\alpha$ -Fehlers (Fehler 1. Art) im Sachzusammenhang.

(2 BE)

Ermittle den Verwerfungsbereich für diesen Test zu einem Signifikanzniveau von $5\,\%.$ Formuliere die Entscheidungsregel im Sachzusammenhang.

(4 BE)

Der Punkt $S$ ist der Schnittpunkt der drei Geraden durch die Punkte $F$ und $C,$ $D$ und $A,$ und $E$ und $B.$
Im ersten Schritt der dargestellten Rechnung wird die Geradengleichung der Geraden durch die Punkte $D$ und $A$ mit der Geradengleichung der Geraden durch die Punkte $E$ und $B$ gleichgesetzt.
Diese Gleichung liefert eine Lösung für $r$ und $s.$ Der ermittelte Wert für $r$ wird dann im zweiten Schritt in die zugehörige Geradengleichung eingesetzt und liefert den Ortsvektor, und damit auch die Koordinaten, des Schnittpunkts $S.$

Rechenweg anzeigen

$\overrightarrow{DE}\circ \overrightarrow{DF} = 150$

Rechenweg anzeigen

$\overrightarrow{DE}\circ \overrightarrow{EF} = -750$

Rechenweg anzeigen

$\overrightarrow{DF}\circ \overrightarrow{EF} = 500$

Da keines dieser Skalarprodukte Null ergibt, liegt in keinem der drei Eckpunkte ein rechter Winkel vor und die Bodenfläche $DEF$ ist somit nicht rechtwinklig.

Größe des Innenwinkels bestimmen

Rechenweg anzeigen

$\alpha = 45^{\circ}$

Länge der Höhe bestimmen

Bezeichne mit $P$ den Punkt, in dem die Höhe $h$ auf die Seite $\overline{EF}$ trifft. Der Innenwinkel des Dreiecks $DEP$ im Punkt $E$ beträgt nach obiger Rechnung $\alpha=45^\circ$ und der Innenwinkel bei $P$ ist ein rechter Winkel. Die Höhe $h$ ist bezüglich des Innenwinkels $\alpha$ die Gegenkathete. Somit folgt:

Rechenweg anzeigen

$h \approx 21,2$

Die Höhe $h$ ist somit ca. $21,2\;[\text{m}]$ lang.

Die obere Etage hat die Form einer Pyramide. Die Höhe der Pyramide entspricht dem Abstand von $G$ zur von $D, E$ und $F$ aufgespannten Ebene.

1. Schritt: Höhe bestimmen

Die drei Punkte $D, E$ und $F$ besitzen die gleiche $z$ -Koordinate, bei der Ebene durch die drei Punkte $D,$ $E$ und $F$ handelt es sich also um eine zur $xy$ -Ebene parallele Ebene. Der Abstand $d$ von $G$ zur Ebene kann somit mit Hilfe der $z$ -Koordinaten berechnet werden:

$d = 35 -15 = 20$

Die Höhe $h_p$ der Pryamide beträgt somit $h_p=20\;\text{m}.$

2. Schritt: Inhalt der Bodenfläche berechnen

Die Bodenfläche der oberen Etage ist das Dreieck $DEF,$ dessen Höhe zur Seite $\overline{EF}$ nach Aufgabenteil c) gegeben ist durch $h =15\cdot\sqrt{2}\;\text{m}.$ Für die Länge der Seite $\overline{EF}$ folgt mit dem CAS:

$\begin{array}[t]{rll} \overline{EF}&=& \left|\overrightarrow{EF} \right| \\[5pt] &=& \left|\pmatrix{-25\\-25\\0} \right| \\[5pt] &=& 25\cdot\sqrt{2}\;[\text{m}] \\[5pt] \end{array}$

Für den Flächeninhalt der Bodenfläche gilt damit:

$A = \dfrac{1}{2}\cdot 15\cdot\sqrt{2} \cdot 25\cdot\sqrt{2}$ $= 375\;[\text{m}^2]$

3. Schritt: Volumen berechnen

$\begin{array}[t]{rll} V&=& \dfrac{1}{3}\cdot h_{p} \cdot A \\[5pt] &=& \dfrac{1}{3}\cdot 20 \cdot 375 \\[5pt] &=& 2500\;[\text{m}^3] \\[5pt] \end{array}$

Das Volumen der oberen Etage beträgt $2500\;\text{m}^3.$ Es werden demnach $25\cdot 0,8 = 20$ Kilowatt benötigt, das heißt $25$ Kilowatt reichen aus.

Die Gerade $AG$ kann durch folgende Gleichung beschrieben werden:

$AG:\overrightarrow{x} = \overrightarrow{OA} + r\cdot \overrightarrow{AG}$ $= \pmatrix{-5\\5\\0} + r\cdot \pmatrix{-5\\5\\35}$

Da das Dreieck $DEF$ in einer zur $xy$ -Ebene parallelen Ebene $H$ liegt und die Punkte $D, E$ und $F$ alle die $z$ -Koordinate $15$ haben, wird die Ebene durch folgende Gleichung beschrieben:

$H:z = 15$

Einsetzen eines allgemeinen Punktes der Gerade $AG$ in die Ebenengleichung liefert:

$\begin{array}[t]{rll} r\cdot 35&=& 15 &\quad \scriptsize \mid\;:35 \\[5pt] r&=& \dfrac{3}{7} \end{array}$

Einsetzen in die Geradengleichung liefert den Schnittpunkt $R:$

$\begin{array}[t]{rll} \overrightarrow{OR}&=& \pmatrix{-5\\5\\0} + \dfrac{3}{7}\cdot \pmatrix{-5\\5\\35} \\[5pt] &=& \pmatrix{-\frac{50}{7}\\ \frac{50}{7}\\ 15} \\[5pt] \end{array}$

Die Koordinaten des Schnittpunkts der Geraden $AG$ und der Ebene, in der das Dreieck $DEF$ liegt, lauten somit $R\left(-\frac{50}{7}\mid \frac{50}{7}\mid 15\right).$

1. Schritt: Geradengleichung aufstellen

Die Strecke $\overline{RG}$ kann mit $t\in[0;1]$ durch folgende Gleichung beschrieben werden:

$\begin{array}[t]{rll} \overrightarrow{x}&=& \overrightarrow{OR} + t\cdot \overrightarrow{RG} \\[5pt] &=& \pmatrix{-\frac{50}{7}\\ \frac{50}{7}\\15} + t\cdot \pmatrix{-\frac{20}{7}\\ \frac{20}{7}\\ 20} \\[5pt] \end{array}$

Der Punkt $Q$ in dem sich der Scheinwerfer befindet hat also Koordinaten der Form $\left(-\frac{50}{7}-\frac{20}{7}t \mid \frac{50}{7}+ \frac{20}{7}t \mid 15+20t\right)$ mit $t\in [0;1].$

2. Schritt: Ebenengleichung aufstellen

Ein Normalenvektor der Ebene $U$ in der $EFG$ liegt ergibt sich mit dem CAS wie folgt:

$\begin{array}[t]{rll} \overrightarrow{n}&=& \overrightarrow{EF}\times \overrightarrow{EG} \\[5pt] &=& \pmatrix{-25\\-25\\0} \times \pmatrix{-10\\-20\\20} \\[5pt] &=& \pmatrix{-500 \\ 500 \\ 250} \\[5pt] &=& 250\cdot \pmatrix{-2\\2\\1} \\[5pt] \end{array}$

Mit dem skalierten Normalenvektor $\overrightarrow{n_1} = \frac{1}{250}\cdot\overrightarrow{n}$ folgt durch Einsetzen der Koordinaten von $E$ in die allgemeine Hessesche Normalenform von $U:$

Rechenweg anzeigen

$d = 75$

Eine Ebenengleichung von $U$ in der Hesseschen Normalenform ist somit gegeben durch:

$U:\dfrac{-2\cdot x +2\cdot y +z-75}{3} = 0$

3. Schritt: Abstand berechnen

Einsetzen der allgemeinen Koordinaten von $Q$ in den Ausdruck für den Abstand zu $U$ und Gleichsetzen mit $5$ liefert:

Rechenweg anzeigen

$\left|t-1\right| = \dfrac{21}{44}$

Nach der Definition des Betrags gilt also $t-1=-\frac{21}{44}$ oder $t-1=\frac{21}{44},$ das heißt für $t$ gilt:

$\begin{array}[t]{rll} t_1&=&\dfrac{23}{44} \\[5pt] t_2&=&\dfrac{65}{44} \end{array}$

Da $t\in[0;1]$ gilt, ist $t_1$ die gesuchte Lösung und für die Koordinaten von Q folgt:

Rechenweg anzeigen

$Q\left(-\dfrac{95}{11} \mid \dfrac{95}{11}\mid \dfrac{280}{11}\right)$

$978\cdot 37\,\% = 978\cdot0,37$ $= 361,86$

$978\cdot(2\,\%+8\,\%) = 978\cdot0,1$ $= 97,8$

2015 wurden somit $361,86$ Millionen Euro Umsatz mit Kaffee gemacht und $97,8$ Millionen Euro Umsatz mit Süßwaren und Eiscreme.

Betrachte die Zufallsgröße $X,$ die die Anzahl der nächsten $150$ Kunden beschreibt, die Kaffee kaufen und binomialverteilt mit $n=150$ und $p=0,37$ ist und die Zufallsgröße $Y,$ die die Anzahl der nächsten $150$ Kunden beschreibt, die Textilien kaufen und binomialverteilt mit $n=150$ und $p=0,07$ ist. Mit dem CAS folgt:

$P(A) = B_{150;0,37}(X\geq 40)$ $= 1 - B_{150;0,37}(X\leq 39)$ $\approx 0,9972 = 99,72\,\%$

$P(B) = B_{150;0,07}(Y \gt 15)$ $= 1- B_{150;0,07}(Y \leq 15)$ $\approx 0,0613 = 6,13\,\%$

Die Wahrscheinlichkeit, dass ein zufällig ausgewählter Kunde Textilien kauft, beträgt $0,07.$ Der Term in Klammern ist somit die Wahrscheinlichkeit dafür, dass von $10$ Kunden höchstens einer Textilien kauft, das heißt der gesamte Term beschreibt die Wahrscheinlichkeit dafür, dass von $10$ Kunden mindestens $2$ Textilien kaufen.

Der $\alpha$ -Fehler bzw. Fehler 1. Art gibt die Wahrscheinlichkeit dafür an, dass die Hypothese verworfen wird, obwohl sie eigentlich wahr ist. Im Sachzusammenhang gibt er also die Wahrscheinlichkeit dafür an, dass der Inhaber seine Hypothese, dass die Hälfte seiner Kunden Kaffee kauft, verwirft, obwohl das eigentlich tatsächlich der Fall ist.

Verwerfungsbereich ermitteln

Die Zufallsgröße $Z,$ die die Anzahl der Kunden beschreibt, die Kaffee kaufen, ist binomialverteilt mit $n=200$ und $p=0,5.$ Da ein zweiseitiger Signifikanztest druchgeführt wird, hat der Verwerfungsbereich die Form $V$ $= \{0;\ldots;k_u\} \cup \{k_o;\ldots;200\}.$ Das das Signifikanzniveau $5\,\%$ beträgt, soll $B_{200;0,5}(Z\leq k_u)\leq0,025$ und $B_{200;0,5}(Z\geq k_o)\leq0,025$ gelten. Systematisches Ausprobieren mit dem CAS liefert:

$B_{200;0,5}(Z\leq 86)\approx0,028$

$B_{200;0,5}(Z\leq 85)\approx0,02$

$B_{200;0,5}(Z\geq 114)$ $= 1 - B_{200;0,5}(Z\leq 113)$ $\approx0,028$

$B_{200;0,5}(Z\geq 115)$ $= 1 - B_{200;0,5}(Z\leq 114)$ $\approx0,02$

Der Verwerfungsbereich ist somit gegeben durch:

$V$ $= \{0;\ldots;85\} \cup \{115;\ldots;200\}.$

Entscheidungsregel formulieren

Sind unter den nächsten 200 Kunden mindestens 86 und höchstens 114 Kaffeekäufer, dann wird angenommen, dass die Hälfte der Kunden Kaffee kauft.