Teil C2

Gegeben ist das Dreieck $ABC$ mit $A(5\mid2\mid4)$ , $B(2\mid-2\mid1)$ und $C(3\mid6\mid2)$ .

Bestimme die Koordinaten eines Punktes $D$ so, dass die Punkte $ABCD$ ein Parallelogramm bilden.

(2 BE)

Ermittle die Koordinaten eines Punktes $T$ , der die Strecke $\overline{AC}$ im Verhältnis $3:1$ teilt.

(2 BE)

Gib die Koordinaten eines Punktes $P$ an, der nicht auf der Strecke $\overline{AC}$ liegt und begründe die Auswahl dieses Punktes.

(1 BE)

Eine Gerade $g$ verläuft durch die Punkte $A$ und $C$ . Die Gerade $g$ schneidet die $x$ - $z$ -Koordinatenebene.
Berechne die Koordinaten dieses Schnittpunktes.

(2 BE)

Die Gerade $g$ wird an der $x$ - $z$ -Ebene gespiegelt.
Gib eine Gleichung der gespiegelten Geraden an.

(1 BE)

Die Stadtverwaltung einer Großstadt führt unter der Bevölkerung eine Befragung zu einem geplanten Bauprojekt durch. Insgesamt werden mehr als 86.000 Fragebögen an alle mindestens 16-jährigen Bürger der Stadt versandt. Vor Auswertung dieser Fragebögen werden von ansässigen Zeitungen bereits mündliche Befragungen unter Besuchern und Markthändlern der Innenstadt durchgeführt und veröffentlicht. Hierbei zeigt sich, dass etwa $60\,\%$ der Befragten das Bauprojekt ablehnen.

Beurteile den Wahrheitsgehalt folgender Aussagen.

„Die Auszählung der offiziellen Fragebögen kann sich die Stadt ersparen. Die Ablehnung des Bauprojektes ist damit schon absolut sicher.“
„Es ist eher unwahrscheinlich, dass die Auszählung der offiziellen Fragebögen eine Befürwortung des Bauprojektes bringen wird. “

(2 BE)

Betrachtet werden die Ereignisse:

$A:$

„Die nächsten 10 Befragten lehnen das Bauprojekt alle ab.“

$B:$

„Genau drei der nächsten 10 Befragten lehnen das Bauprojekt ab.“

$C:$

„Unter den nächsten 10 Befragten lehnt mehr als die Hälfte das Bauprojekt ab.“

$D:$

„Die Zahl der Projektgegner weicht bei den nächsten 10 Befragten um höchstens zwei vom Erwartungswert ab.“

Erläutere, aufgrund welcher Bedingungen für die Berechnung der Wahrscheinlichkeiten dieser Ereignisse das Modell der Binomialverteilung angenommen werden kann.
Berechnen die Wahrscheinlichkeiten dieser Ereignisse, wenn $60\,\%$ der Befragten das Bauprojekt ablehnen.

(6 BE)

In einer groß angelegten Kampagne wurde für das Bauprojekt geworben. Nun glauben die Befürworter, dass die Mehrheit der Bevölkerung für eine Bebauung votieren wird $(H_1: p_1 = 0,51)$ , während die Gegner weiterhin von nur $40\,\%$ Befürwortern ausgehen $(H_0: p_0 = 0,40)$ . Um hierfür eine Prognose zu treffen, soll ein Alternativtest genutzt werden, zu dem $100$ zufällig ausgewählte Bürger mündlich befragt werden.
Konstruiere einen solchen Alternativtest, bei dem die Summe der Fehler erster und zweiter Art minimal wird.
Bestimme hierfür den Annahme- und Ablehnungsbereich für $H_0$ .

(4 BE)

Bei einem Parallelogramm sind gegenüberliegende Seiten gleichlang und parallel. Für $D$ folgt damit:

$\begin{array}[t]{rll} \overrightarrow{OD}&=&\overrightarrow{OA}+\overrightarrow{BC} \\[5pt] &=&\pmatrix{5\\2\\4} + \pmatrix{3-2\\6-(-2)\\2-1}\\[5pt] &=&\pmatrix{6\\10\\5} \end{array}$

Der Punkt $D$ besitzt somit die Koordinaten $D( 6\mid 10 \mid 5).$

Rechenweg anzeigen

$\overrightarrow{OT} = \pmatrix{\frac{7}{2}\\5\\\frac{5}{2}}$

Der Punkt $T$ besitzt somit die Koordinaten $T\left(\frac{7}{2}\mid5\mid \frac{5}{2}\right).$

Der Ortsvektor eines allgemeinen Punkts $Q$ auf der Strecke $\overline{AC}$ ist gegeben wie folgt:

$\overrightarrow{OQ}=\overrightarrow{OA}+ \lambda \cdot \overrightarrow{AC},\quad \lambda \in \left[0;1 \right]$

Wahl eines Werts $\lambda \not\in \left[0;1 \right]$ liefert einen Punkt, der zwar auf der Geraden durch die Punkte $A$ und $C$ liegt, aber nicht auf der Strecke $\overline{AC}.$ Ein möglicher Punkt $P$ ergibt sich somit mit Hilfe des CAS beispielsweise als:

$\begin{array}[t]{rll} \overrightarrow{OP}&=&\overrightarrow{OA}+2 \cdot \overrightarrow{AC} \\[5pt] &=&\pmatrix{1\\10\\0} \end{array}$

Ein möglicher Punkt $P$ besitzt damit die Koordinaten $P \left( 1 \mid 10 \mid 0\right).$

Eine mögliche Geradengleichung von $g$ lautet wie folgt:

$g:\overrightarrow{x}=\overrightarrow{OA}+ t \cdot \overrightarrow{AC}$ $= \pmatrix{5\\2\\4}+t\cdot\pmatrix{-2\\4\\-2}$

Ein allgemeiner Punkt der $x$ - $z$ -Ebene besitzt die Koordinaten $(x\mid0\mid z).$ Gleichsetzen mit der Geradengleichung von $g$ liefert folgendes lineares Gleichungssystem:

$\begin{array}{lrll} \text{I}\quad&x&=& 5 -2t &\quad \\ \text{II}\quad&0&=& 2 + 4t &\quad \\ \text{III}\quad&z&=& 4 - 2t &\quad \\ \end{array}$

Mit Hilfe des CAS folgt für die Lösungen des Gleichungssystems:

$\begin{array}[t]{rll} t&=&-\dfrac{1}{2} \\[5pt] x&=&6 \\[5pt] z&=&5 \end{array}$

Der Schnittpunkt $S$ der Geraden $g$ mit der $x$ - $z$ -Ebene besitzt somit die Koordinaten $S(6 \mid 0 \mid 5).$

Da der Punkt $S(6 \mid 0 \mid 5)$ auf der Gerade $g$ und in der $x$ - $z$ -Ebene liegt, verändert er sich bei einer Spiegelung der Geraden an der Ebene nicht.
Bei allen weiteren Punkte der Geraden $g$ ändert sich das Vorzeichen der $y$ -Koordinate. Spiegelung des Punktes $A,$ welcher auf der Geraden $g$ liegt, an der $x$ - $z$ -Ebene liefert somit einen Punkt $\(A$ mit den Koordinaten $\(A$ Eine mögliche Geradengleichung der gespiegelten Geraden $h$ lautet somit:

$\(h:\overrightarrow{x}=\overrightarrow{OS}+s\cdot\overrightarrow{SA$ $= \pmatrix{6\\0\\5} + s \cdot \pmatrix{-1\\-2\\-1}$

Beurteilen der ersten Aussage

Die getroffene Aussage ist falsch, da die Stichprobe der befragten Leute zufälligerweise einen größeren Anteil der Gegner des Bauprojekts enthalten haben könnte, selbst wenn diese innerhalb der gesamten Bevölkerung in der Minderheit wären. Absolute Sicherheit über das erzielte Ergebnis liefert nur eine Befragung aller Bürger.

Beurteilen der zweiten Aussage

Diese Aussage kann sowohl richtig als auch falsch sein. Die erzielte Quote von $60\,\%$ für die Ablehnung des Bauprojekts bei der Befragung deutet darauf hin, dass auch innerhalb der gesamten Bevölkerung mehr Leute gegen das Bauprojekt sind. Falls die Menge der Leute die befragt wurden allerdings sehr klein war, kann es trotzdem sein, dass die Auswertung der Fragebögen eine Befürwortung des Bauprojektes bringen wird.

Annahme der Binomialverteilung erläutern

Bei der Umfrage wird ermittelt, ob ein Bürger für oder gegen das Bauprojekt stimmt, damit gibt es nur zwei mögliche Ausgänge. Weiterhin ist die Wahrscheinlichkeit, dass eine befragte Person das Projekt ablehnt, immer gleich, da davon ausgegangen werden kann, dass die Befragten sich nicht vorher untereinander abstimmen, welche Antwort sie geben.

Wahrscheinlichkeiten der Ereignisse bestimmen

Die Zufallsvariable $X,$ die die Anzahl der Befragten angibt, die das Bauprojekt ablehnen, ist binomialverteilt mit den Parametern $n=10$ und $p=0,6.$ Mit dem CAS folgt:

$\begin{array}[t]{rll} P(A)&=&B_{10;0,6}(X=10) \\[5pt] &\approx&0,0060 \\[5pt] &=&0,6\,\% \end{array}$

$\begin{array}[t]{rll} P(B)&=&B_{10;0,6}(X=3) \\[5pt] &\approx&0,0425 \\[5pt] &=&4,25\,\% \end{array}$

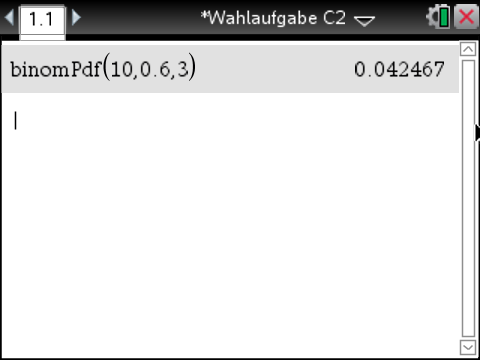
Mathematische Berechnung mit binomPdf-Funktion auf einem Taschenrechner.

$\begin{array}[t]{rll} P(C)&=&B_{10;0,6}(X\gt5) \\[5pt] &=&B_{10;0,6}(X\geq6) \\[5pt] &\approx&0,6331 \\[5pt] &=&63,31\,\% \end{array}$

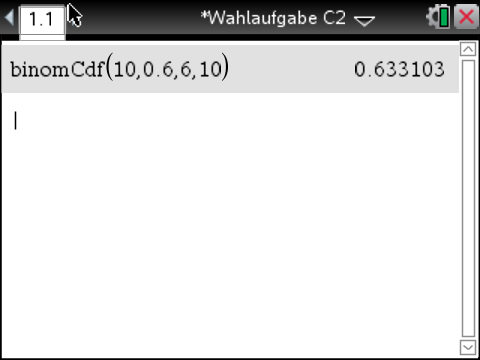
Bildschirm mit Berechnung der binomialen kumulierten Verteilungsfunktion und Ergebnis.

Der Erwartungswert der Zufallsvariable $X$ ist gegeben als $\mu = n\cdot p = 6.$ Somit folgt mit dem CAS:

$\begin{array}[t]{rll} P(D)&=&B_{10;0,6}(4\leq X\leq8) \\[5pt] &\approx&0,8989 \\[5pt] &=&89,89\,\% \end{array}$

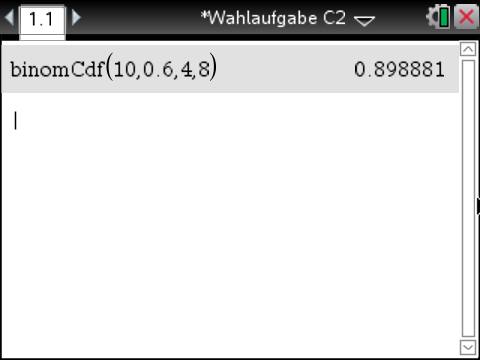
Bildschirmansicht eines Rechners mit einer Berechnung der binomialen kumulativen Verteilung.

Die Zufallsvariable $Y,$ die die Anzahl der Befürworter angibt, ist für den Fehler erster Art binomialverteilt mit den Paramtern $n=100$ und $p=p_0=0,4$ und für den Fehler zweiter Art binomialverteilt mit den Parametern $n=100$ und $p=p_1=0,51.$
Für die Minimierung der Summe der beiden Fehler wird ein $k$ gesucht, das den Annahmebereich $A=\{0,1,\ldots k\}$ und den Verwerfungsbereich $V=\{k+1,k+2,\ldots,100\}$ für $H_0$ festlegt, sodass der folgende Ausdruck minimal wird:

$B_{100;0,4}(X\geq k+1)+B_{100;0,51}(X\leq k)$

Systematisches Ausprobieren mit Hilfe des CAS liefert:

$k=45$

Somit ergeben sich für den Annahmebereich bzw. Verwerfungsbereich von $H_0$ die Mengen $A=\{0,1,\ldots 45\}$ bzw. $V=\{46,47,\ldots,100\}.$

Bei einem Parallelogramm sind gegenüberliegende Seiten gleichlang und parallel. Für $D$ folgt damit:

$\begin{array}[t]{rll} \overrightarrow{OD}&=&\overrightarrow{OA}+\overrightarrow{BC} \\[5pt] &=&\pmatrix{5\\2\\4} + \pmatrix{3-2\\6-(-2)\\2-1}\\[5pt] &=&\pmatrix{6\\10\\5} \end{array}$

Der Punkt $D$ besitzt somit die Koordinaten $D( 6\mid 10 \mid 5).$

Rechenweg anzeigen

$\overrightarrow{OT} = \pmatrix{\frac{7}{2}\\5\\\frac{5}{2}}$

Der Punkt $T$ besitzt somit die Koordinaten $T\left(\frac{7}{2}\mid5\mid \frac{5}{2}\right).$

Der Ortsvektor eines allgemeinen Punkts $Q$ auf der Strecke $\overline{AC}$ ist gegeben wie folgt:

$\overrightarrow{OQ}=\overrightarrow{OA}+ \lambda \cdot \overrightarrow{AC},\quad \lambda \in \left[0;1 \right]$

$\begin{array}[t]{rll} \overrightarrow{OP}&=&\overrightarrow{OA}+2 \cdot \overrightarrow{AC} \\[5pt] &=&\pmatrix{1\\10\\0} \end{array}$

Ein möglicher Punkt $P$ besitzt damit die Koordinaten $P \left( 1 \mid 10 \mid 0\right).$

Eine mögliche Geradengleichung von $g$ lautet wie folgt:

$g:\overrightarrow{x}=\overrightarrow{OA}+ t \cdot \overrightarrow{AC}$ $= \pmatrix{5\\2\\4}+t\cdot\pmatrix{-2\\4\\-2}$

Ein allgemeiner Punkt der $x$ - $z$ -Ebene besitzt die Koordinaten $(x\mid0\mid z).$ Gleichsetzen mit der Geradengleichung von $g$ liefert folgendes lineares Gleichungssystem:

$\begin{array}{lrll} \text{I}\quad&x&=& 5 -2t &\quad \\ \text{II}\quad&0&=& 2 + 4t &\quad \\ \text{III}\quad&z&=& 4 - 2t &\quad \\ \end{array}$

Mit Hilfe des CAS folgt für die Lösungen des Gleichungssystems:

$\begin{array}[t]{rll} t&=&-\dfrac{1}{2} \\[5pt] x&=&6 \\[5pt] z&=&5 \end{array}$

Der Schnittpunkt $S$ der Geraden $g$ mit der $x$ - $z$ -Ebene besitzt somit die Koordinaten $S(6 \mid 0 \mid 5).$

$\(h:\overrightarrow{x}=\overrightarrow{OS}+s\cdot\overrightarrow{SA$ $= \pmatrix{6\\0\\5} + s \cdot \pmatrix{-1\\-2\\-1}$

Beurteilen der ersten Aussage

Beurteilen der zweiten Aussage

Annahme der Binomialverteilung erläutern

Wahrscheinlichkeiten der Ereignisse bestimmen

Die Zufallsvariable $X,$ die die Anzahl der Befragten angibt, die das Bauprojekt ablehnen, ist binomialverteilt mit den Parametern $n=10$ und $p=0,6.$ Mit dem CAS folgt:

$\begin{array}[t]{rll} P(A)&=&B_{10;0,6}(X=10) \\[5pt] &\approx&0,0060 \\[5pt] &=&0,6\,\% \end{array}$

$\begin{array}[t]{rll} P(B)&=&B_{10;0,6}(X=3) \\[5pt] &\approx&0,0425 \\[5pt] &=&4,25\,\% \end{array}$

Mathematische Berechnung mit binomialPDF-Funktion und Ergebnis.

$\begin{array}[t]{rll} P(C)&=&B_{10;0,6}(X\gt5) \\[5pt] &=&B_{10;0,6}(X\geq6) \\[5pt] &\approx&0,6331 \\[5pt] &=&63,31\,\% \end{array}$

Berechnung der binomialen kumulativen Verteilung mit Werten und Ergebnis.

Der Erwartungswert der Zufallsvariable $X$ ist gegeben als $\mu = n\cdot p = 6.$ Somit folgt mit dem CAS:

$\begin{array}[t]{rll} P(D)&=&B_{10;0,6}(4\leq X\leq8) \\[5pt] &\approx&0,8989 \\[5pt] &=&89,89\,\% \end{array}$

Berechnung der binomialen kumulativen Verteilungsfunktion mit Ergebnissen.

$B_{100;0,4}(X\geq k+1)+B_{100;0,51}(X\leq k)$

Systematisches Ausprobieren mit Hilfe des CAS liefert:

$k=45$

Somit ergeben sich für den Annahmebereich bzw. Verwerfungsbereich von $H_0$ die Mengen $A=\{0,1,\ldots 45\}$ bzw. $V=\{46,47,\ldots,100\}.$