Teil B

Für jede positive reelle Zahl $a$ ist eine Funktion $f_a$ durch

$f_a(x)=\dfrac{5}{3a^3}\cdot(x-a)^2\cdot(x+a)^2$ mit $x\in\mathbb{R}$ gegeben.

Gib drei gemeinsame Eigenschaften der Graphen von $f_a$ an, die von $a$ nicht beeinflusst werden.

(3 BE)

Untersuche die Graphen von $f_a$ auf lokale Extrempunkte und auf Wendepunkte.
Gib die Koordinaten dieser Punkte an.

[Zur Kontrolle: $W_1\left(\frac{a}{3}\sqrt3 \,\bigg \vert \, \frac{20}{27}a\right)$ ]

(6 BE)

Zeige, dass die Größe des Schnittwinkels der Wendetangenten unabhängig von $a$ ist.

(3 BE)

Für jeden Wert von $a$ bilden die Wendepunkte, der Hochpunkt und der Koordinatenursprung ein Viereck.

Stelle diesen Sachverhalt für den Graphen von $f_8$ dar.

Berechne den Flächeninhalt dieses Vierecks in Abhängigkeit von $a$ .
Untersuche, ob es einen Wert für $a$ so gibt, dass das Viereck ein Quadrat ist.

(7 BE)

Für die Teilaufgaben e) und f) gilt $a=8.$

In die Fläche, die vom Graphen von $f_8$ und der $x$ -Achse vollständig begrenzt wird, soll ein Quadrat gelegt werden. Eine Seite des Quadrates liegt auf der $x$ -Achse und die anderen beiden Eckpunkte liegen auf dem Graphen von $f_8$ .

Berechne den Flächeninhalt des Quadrates.

(3 BE)

Der Graph von $f_8$ wird

an der $x$ -Achse gespiegelt.
an der $y$ -Achse gespiegelt.
so verschoben, dass das Bild des Graphen durch den Koordinatenursprung verläuft.
so gestaucht, dass die Tiefpunkte erhalten bleiben und die $y$ -Koordinate des Hochpunktes halbiert wird.

Gib für jeden dieser Fälle eine Funktionsgleichung an.

(4 BE)

Auf dem Dach einer Firma ist eine Photovoltaikanlage installiert.
Die Graphen zeigen für zwei Tage die Leistung der Photovoltaikanlage in Abhängigkeit von der Uhrzeit. Die Leistung $P$ wird in Kilowatt (kW) angegeben. Die zu einem Zeitpunkt bereitgestellte Energie lässt sich als Flächeninhalt der Fläche unter der Kurve interpretieren. Die Energie $E$ wird in Kilowattstunden (kWh) angegeben.

„Unter Photovoltaik... versteht man die direkte Umwandlung von Lichtenergie, meist aus Sonnenlicht, in elektrische Energie mittels Solarzellen.“

Aus: https://de.m.wikipedia.org (18.06.2018)

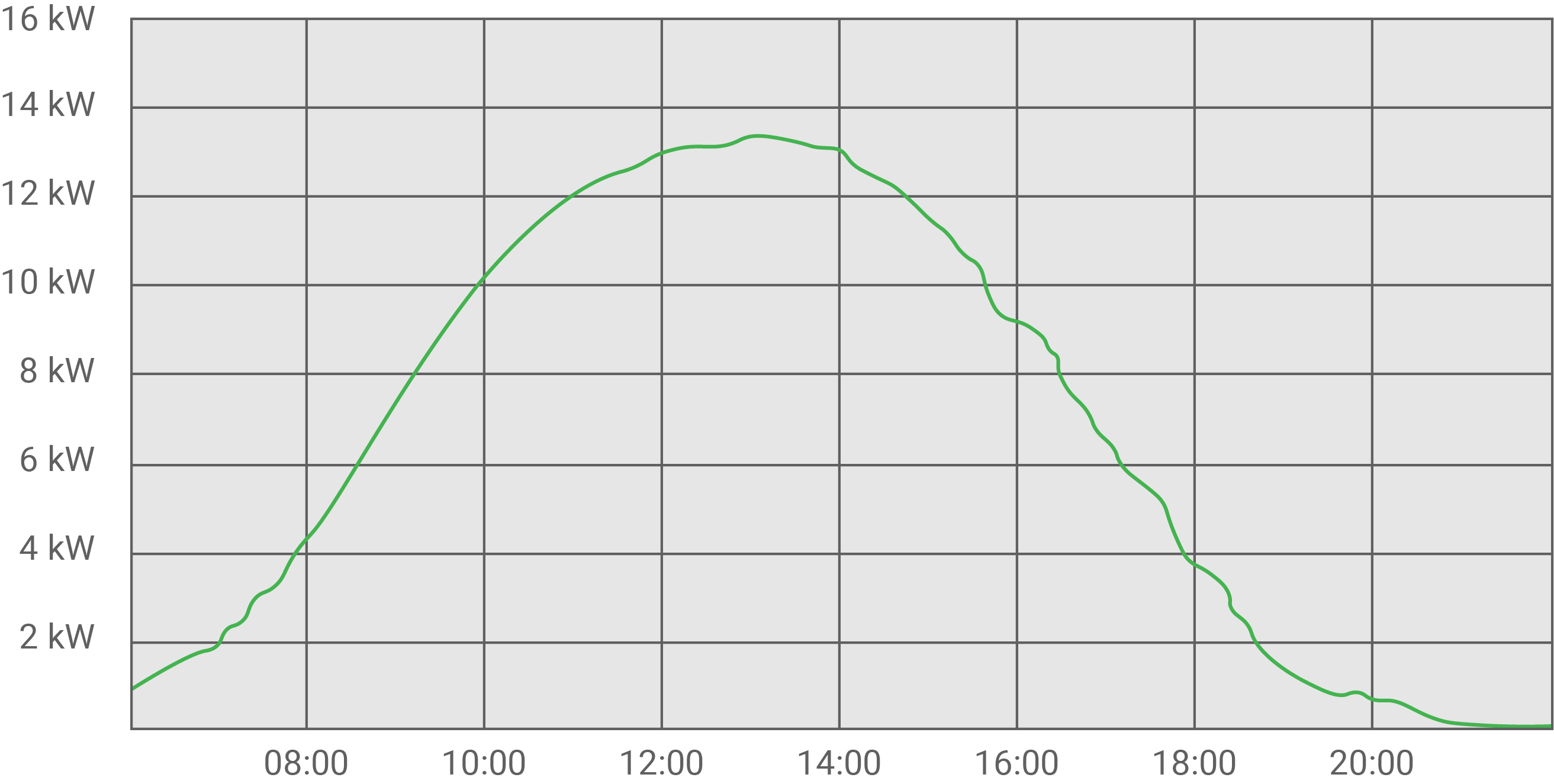
thüringen mathe abi 2018 teil b abbildung 1

04.07.2015

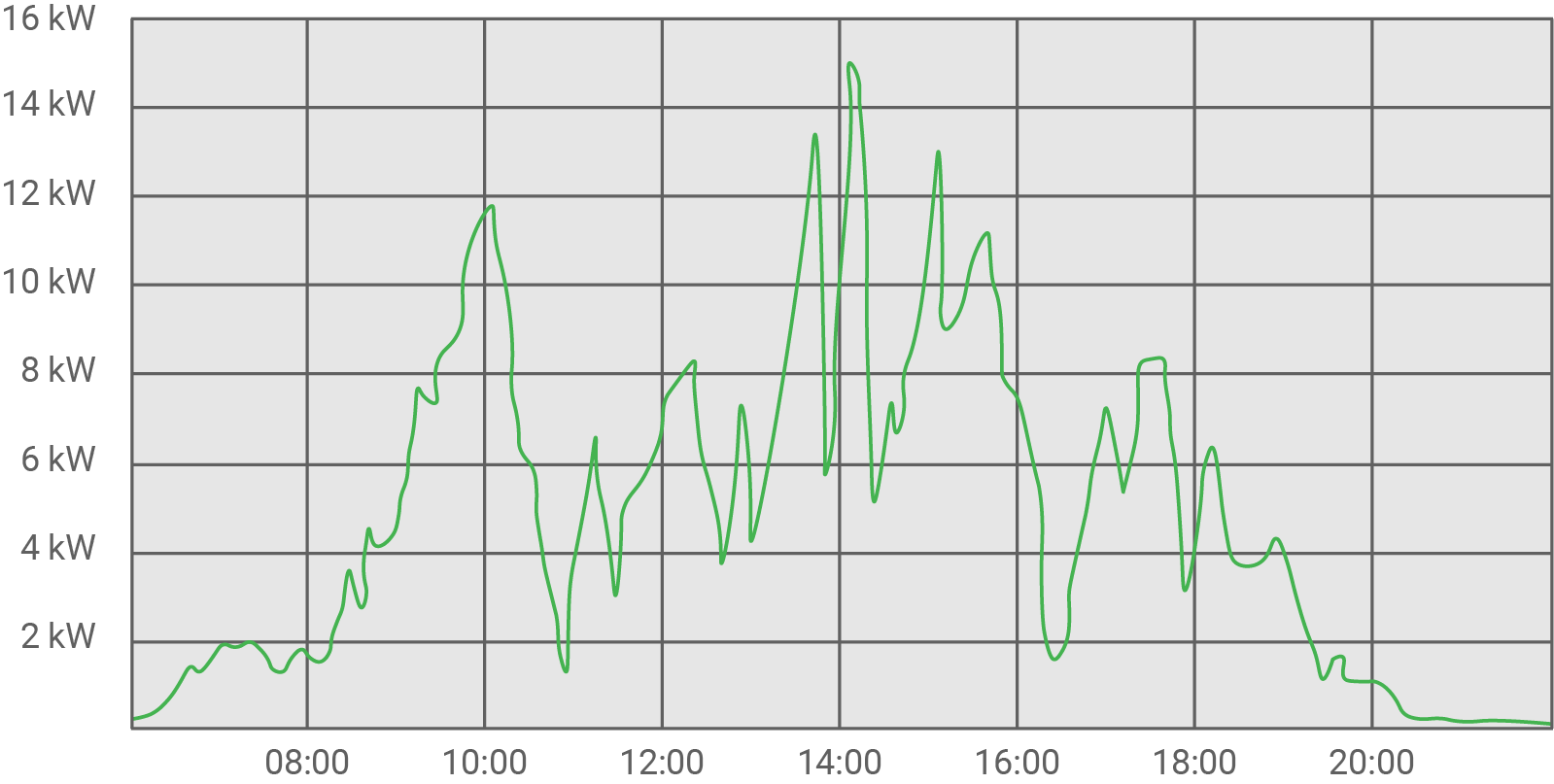
thüringen mathe abi 2018 teil b abbildung 2

20.07.2015

Schlussfolgere unter Nutzung der Diagramme auf das Wetter an beiden Tagen.

(2 BE)

Die am 20.07.2015 insgesamt bereitgestellte Energie in kWh soll abgeschätzt werden.

Erläutere ein Vorgehen, um einen groben Schätzwert zu erhalten.
Gib deinen Schätzwert entsprechend deines gewählten Verfahrens an.

(3 BE)

Begründe, dass eine Verschiebung des Graphen von $f_8$ aus Aufgabe 1 mit $f_8(x)=\frac{5}{1536}\cdot(x-8)^2\cdot(x+8)^2$ entlang der $x$ -Achse eine gute Näherung für die Leistung am 04.07.2015 ist.

Berechne die von der Anlage an diesem Tag insgesamt bereitgestellte Energie in kWh.

(5 BE)

Am 04.07.2015 wurden zu Arbeitsbeginn um 07:00 Uhr die elektrischen Anlagen der Firma eingeschaltet und zu Arbeitsende um 17:00 Uhr ausgeschaltet. Die dafür benötigte Leistung kann im Intervall $7\leq x\leq 17$ durch eine Funktion $h$ mit

$h(x)=-\frac{1}{100}\cdot(x-7)\cdot(x-17)^3$

beschrieben werden.
Der Wert von $x$ entspricht der aktuellen Uhrzeit in Stunden.
Es gab einen Zeitraum, in dem die durch die Photovoltaikanlage bereitgestellte Leistung nicht ausreichte, um den Bedarf der Firma abzudecken.

Ermittle diesen Zeitraum.

(4 BE)

Da $a\gt 0$ und $a\in\mathbb{R}$ gilt, folgt:

Die Graphen aller Funktionen $f_a$ sind achsensymmetrisch zur $y$ -Achse
Alle Funktionen $f_a$ haben genau zwei doppelte Nullstellen
Alle Funktionen $f_a$ nehmen keine negativen Werte an

Graphen auf lokale Extrempunkte untersuchen

Ableiten von $f$ mit dem CAS liefert:

$\(f_a$

1. Schritt: Notwendiges Kriterium für Extremstellen anwenden

$\(f$

Mit Hilfe des solve-Befehls des CAS folgt:

$\begin{array}[t]{rll} x_1&=& -a \\[5pt] x_2&=& 0 \\[5pt] x_3&=& a \end{array}$

2. Schritt: Hinreichendes Kriterium für Extremstellen überprüfen

Der CAS liefert:

$\(f_a$

Der Graph von $f_a$ besitzt somit an den Stellen $x_1 = -a$ und $x_3 =a$ jeweils einen Tiefpunkt und an der Stelle $x_2=0$ einen Hochpunkt.

3. Schritt: Koordinaten berechnen

Mit dem CAS folgt:

$\begin{array}[t]{rll} f_a(-a)&=& 0 \\[5pt] f_a(0)&=& \dfrac{5}{3}a \\[5pt] f_a(a)&=& 0 \\[5pt] \end{array}$

Die Graphen von $f_a$ besitzen damit zwei Tiefpunkte mit den Koordinaten $T_1(-a\mid 0)$ und $T_2(a\mid 0)$ sowie einen Hochpunkt mit den Koordinaten $H\left(0\mid \frac{5}{3}a\right).$

Graphen auf Wendepunkte untersuchen

Ableiten von $\(f$ im CAS liefert:

$\(f_a$

1. Schritt: Notwendiges Kriterium für Wendestellen anwenden

$\(f$

Mit dem solve-Befehl des CAS folgt:

$\begin{array}[t]{rll} x_1&=& -a\cdot \dfrac{\sqrt{3}}{3} \\[5pt] x_2&=& a\cdot \dfrac{\sqrt{3}}{3} \\[5pt] \end{array}$

2. Schritt: Hinreichendes Kriterium für Wendestellen überprüfen

Der CAS liefert:

$\(f_a$ $= -40\cdot \dfrac{\sqrt{3}}{3a^2} \neq 0$

$\(f_a$ $= 40\cdot \dfrac{\sqrt{3}}{3a^2} \neq 0$

3. Schritt: Koordinaten berechnen

Mit dem CAS folgt:

$\begin{array}[t]{rll} f_a\left(-a\cdot \dfrac{\sqrt{3}}{3}\right) &=& \dfrac{20a}{27} \\[5pt] f_a\left(a\cdot \dfrac{\sqrt{3}}{3}\right) &=& \dfrac{20a}{27} \\[5pt] \end{array}$

Der Graph von $f_a$ besitzt somit die beiden Wendepunkte $W_1\left(-a\cdot \frac{\sqrt{3}}{3} \mid \frac{20a}{27} \right)$ und $W_2\left(a\cdot \frac{\sqrt{3}}{3} \mid \frac{20a}{27} \right).$

Mit Hilfe des CAS folgt für die Steigung der beiden Wendetangenten von $f_a:$

$\(\begin{array}[t]{rll} m_1 &=& f_a$

Beide Steigungswerte sind unabhängig von $a.$ Da die Formel für den Schnittwinkel zweier Geraden aber nur von den Steigungswerten der beiden Geraden abhängt, hängt auch der Schnittwinkel nicht von $a$ ab.

Sachverhalt darstellen

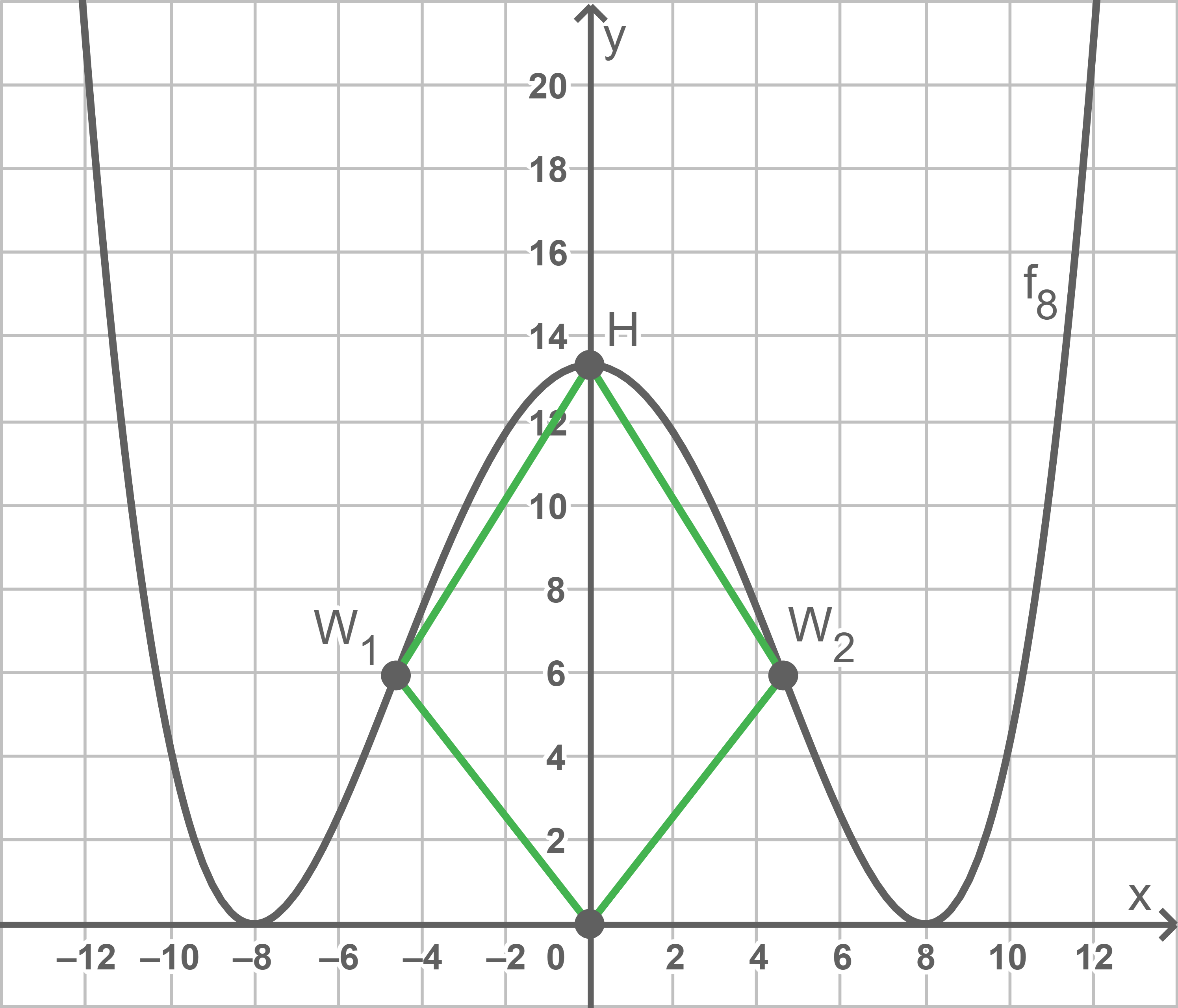Flächeninhalt berechnen

Bei den Vierecken handelt es sich um Drachenvierecke. Für die Längen der Diagonalen gilt:

$\left|\overline{OH} \right| = \dfrac{5}{3}a$

$\left|\overline{W_1W_2} \right|$ $= a\cdot \dfrac{\sqrt{3}}{3} - \left(-a\cdot \dfrac{\sqrt{3}}{3} \right)$ $= 2\cdot a\cdot \dfrac{\sqrt{3}}{3}$

Für den Flächeninhalt folgt somit:

$A(a) = \dfrac{1}{2}\cdot\left|\overline{OH} \right|\cdot\left|\overline{W_1W_2} \right|$ $= \dfrac{1}{2}\cdot \dfrac{5}{3}a \cdot 2\cdot a\cdot \dfrac{\sqrt{3}}{3}$ $= \dfrac{5\sqrt{3}}{9}a^2$

Quadrat überprüfen

Bei einem Quadrat sind insbesondere die beiden Diagonalen gleich lang. Gleichsetzen von $\left|\overline{OH} \right|$ mit $\left|\overline{W_1W_2} \right|$ und auflösen nach $a$ mit dem solve-Befehl des CAS liefert:

$a=0$

Da $a$ als eine positive reelle Zahl vorgegeben ist, gibt es somit keinen Wert von $a,$ sodass das Viereck ein Quadrat ist.

Da der Graph von $f_8$ symmetrisch zur $y$ -Achse liegt, liegt auch das beschriebene Quadrat symmetrisch zur $y$ -Achse. Die Breite des Vierecks wird durch die $x$ -Koordinaten der Eckpunkte bestimmt, die Höhe durch die $y$ -Koordinate der oberen Eckpunkte. Die oberen Eckpunkte des Quadrats sind gegeben durch $(-u\mid f_8(-u))$ und $(u\mid f_8(u)),$ wobei $f_8(-u)=f_8(u)$ gilt. Damit es sich um ein Quadrat handelt, muss somit $f_8(u)= 2\cdot u$ gelten. Mit dem solve-Befehl des CAS folgt:

$u_1\approx 3,89$

$u_2\approx 12,28$

Der Wert $u_2$ liegt außerhalb des betrachteten Bereichs, da $u$ durch die beiden Nullstellen von $f_8$ bei $-8$ und $8$ begrenzt ist.
Für den Flächeninhalt folgt somit:

$A = (2\cdot u_1)^2$ $\approx 60,53\;[\text{FE}]$

$1.$

$g_1(x) = -f_8(x)$ $= -\dfrac{5}{3\cdot 8^3} \cdot (x-8)^2\cdot (x+8)^2$

$2.$

Der Graph von $f_8$ ist symmetrisch zur $y$ -Achse. Somit folgt:

$g_2(x) = f_8(x)$ $= \dfrac{5}{3\cdot 8^3}\cdot (x-8)^2\cdot (x+8)^2$

$3.$

Der Graph kann beispielsweise so verschoben werden, dass der Hochpunkt des Graphen im Koordinatenursprung liegt:

$g_3(x)= f_8(x)-\dfrac{40}{3}$ $= \dfrac{5}{3\cdot 8^3}\cdot (x-8)^2\cdot (x+8)^2$ $-\dfrac{40}{3}$

$4.$

Da die Tiefpunkte des Graphen von $f_8$ auf der $x$ -Achse liegen, ändern sich ihre Koordinaten durch eine Stauchung des Graphen in $y$ -Richtung nicht. Somit ist eine mögliche Funktionsgleichung gegeben durch:

$g_4(x)= \dfrac{1}{2}\cdot f_8(x)$ $= \dfrac{5}{6\cdot 8^3}\cdot (x-8)^2\cdot (x+8)^2$

Am 4.7.2015 verläuft der Graph der Leistung der Anlage sehr gleichmäßig, ähnlich wie durch den Verlauf des Sonnenstands erwartet wird. Der Himmel war an diesem Tag somit vermutlich wolkenfrei.
Am 20.7.2015 verläuft der Graph an vielen Stellen sehr sprunghaft. Eine mögliche Ursache hierfür ist wechselhafte Bewölkung.

Vorgehen erläutern

Die insgesamt bereitgestellte Energie am 20.07.2015 entspricht dem Flächeninhalt der Fläche unter dem zugehörigen Graphen. Diese Fläche kann in diesem Fall beispielsweise angenähert werden, indem die jeweilige Menge eines Rechtecks die unter dem Graphen liegt mit der anderer Rechtecke zusammengefasst wird, um dann anschließend die Menge der vollständigen Rechtecke zu zählen.

Schätzwert angeben

Die oben beschriebenen Vorgehehensweise liefert zwischen $16$ und $19$ ganze Rechtecke. Ein Rechteck entspricht hierbei $2\cdot 2 = 4\;[\text{kWh}].$ Insgesamt ergibt sich somit ein Schätzwert von zwischen $4\cdot16 = 64\;[\text{kWh}]$ und $4\cdot19 = 76\;[\text{kWh}].$

Gute Näherung begründen

Der $y$ -Wert des Hochpunktes des Graphen von $f_8$ liegt ähnlich wie im Diagramm der Leistung am 04.07.2015 bei $13,3.$ Für eine gute Näherung muss der Graph von $f_8$ so entlang der $x$ -Achse verschoben werden, dass der Hochpunkt an der Stelle $x\approx 13$ liegt. Es ergibt sich folgender Funktionsterm:

$g(x) = f_8(x-13)$ $= \dfrac{5}{1536}\cdot (x-13-8)^2\cdot (x-13+8)^2$ $= \dfrac{5}{1536}\cdot (x-21)^2\cdot (x-5)^2$

Mit dem solve-Befehl des CAS folgt für die Nullstellen von $g:$

$\begin{array}[t]{rll} x_1&=&5 \\[5pt] x_2&=&21 \end{array}$

Vergleicht man den Verlauf des Graphen im ersten Diagramm, lässt sich auch hier schätzen, dass sich die Leistung etwa um $5:00$ Uhr und $21:00$ Uhr Null annähert. Dazwischen verläuft sowohl der Graph von $g$ als auch der Graph der Leistung nahezu parabelförmig mit einem in etwa gleichen Hochpunkt.

Insgesamt ist der verschobene Graph von $f_8$ damit eine gute Näherung für die Leistung am 04.07.2015.

Bereitgestellte Energie berechnen

Mit dem CAS folgt für die von der Anlage bereitgestellte Energie $E:$

Rechenweg anzeigen

$E \approx 114\;[\text{kWh}]$

In dem gesuchten Zeitraum nimmt die Funktion $g$ kleinere Werte als die Funktion $h$ an, das heißt dort gilt $g(x) \lt h(x).$ Mit dem solve-Befehl des CAS folgt für $x:$

$7,39 \lt x \lt 10,14$

Mit $0,39\cdot 60 \approx 23$ und $0,14\cdot 60 \approx 8$ folgt somit, dass im Zeitraum von ca. $07:23$ Uhr bis $10:08$ Uhr die bereitgestellte Leistung der Photovoltaikanlage nicht ausreichte, um den Bedarf der Firma zu decken.