Wahlaufgaben
5
Gegeben ist für jede positive reelle Zahl  die in
die in  definierte Funktion
definierte Funktion  mit
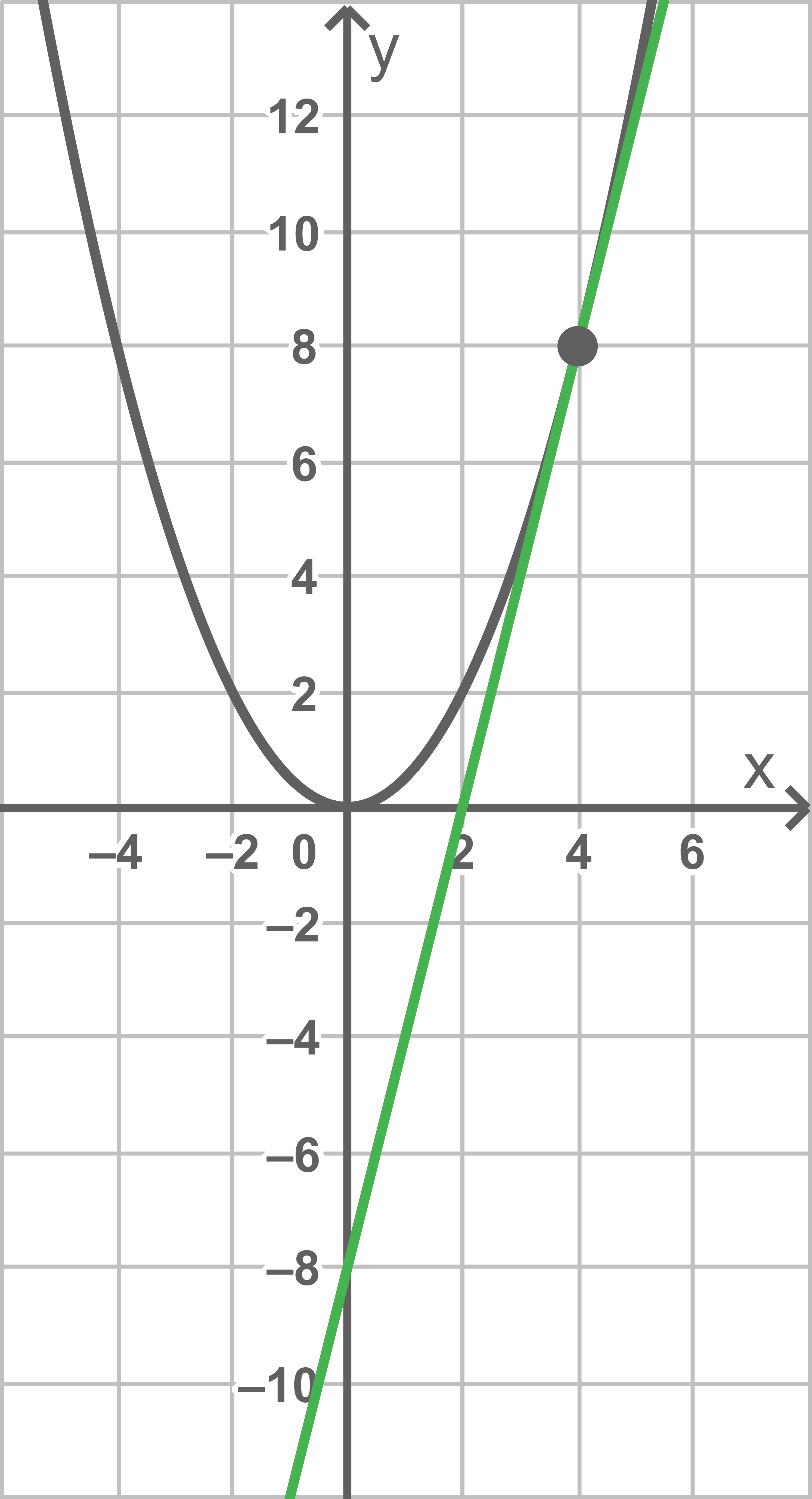
mit  Die Abbildung zeigt den Graphen von
Die Abbildung zeigt den Graphen von  sowie die Tangente
sowie die Tangente  an den Graphen von
an den Graphen von  im Punkt
im Punkt  .
.

a)
Gib anhand der Abbildung eine Gleichung der Tangente  an.
an.
(1 BE)
b)
Weise nach, dass für jeden Wert für  die Tangente an den Graphen von
die Tangente an den Graphen von  im Punkt
im Punkt  die
die  -Achse im Punkt
-Achse im Punkt  schneidet.
schneidet.
(4 BE)
6
Für eine Zahl  zeigt die Abbildung den Graphen
zeigt die Abbildung den Graphen  der in
der in  definierten Funktion
definierten Funktion  mit
mit  sowie die Gerade
sowie die Gerade 
 und
und  schneiden sich im Koordinatenursprung und
schneiden sich im Koordinatenursprung und  verläuft senkrecht zur Tangente an
verläuft senkrecht zur Tangente an  im Koordinatenursprung. Zudem berühren sich
im Koordinatenursprung. Zudem berühren sich  und die
und die  -Achse im Punkt
-Achse im Punkt 
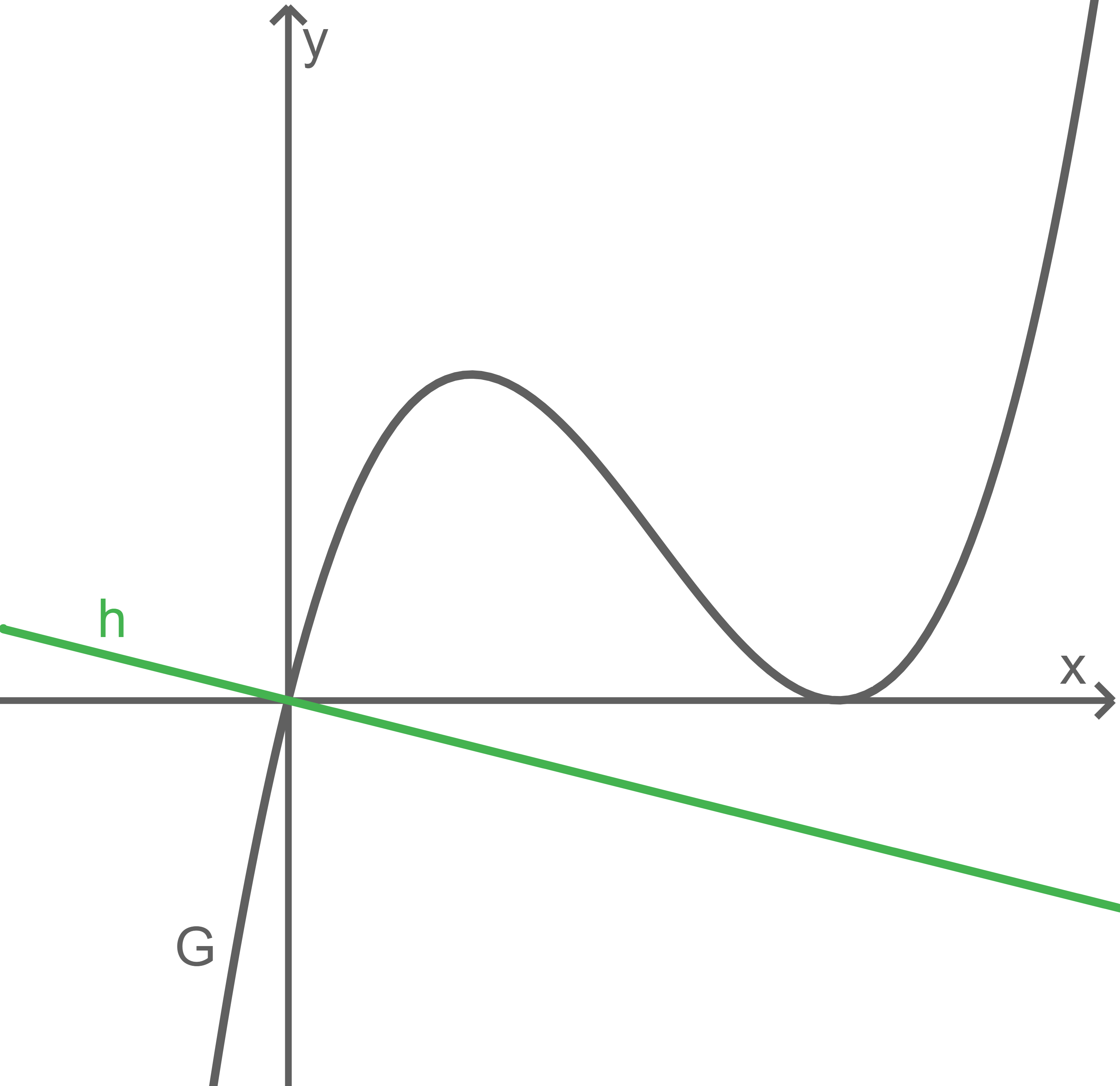 Betrachtet wird dasjenige Rechteck, das die folgenden Eigenschaften besitzt:
Betrachtet wird dasjenige Rechteck, das die folgenden Eigenschaften besitzt:
Skizziere das Rechteck in der Abbildung und zeige, dass der Flächeninhalt des Rechtecks unabhängig von 
- Die beiden gemeinsamen Punkte von
und der
-Achse sind zwei benachbarte Eckpunkte des Rechtecks.
- Eine Diagonale liegt auf der Geraden
(5 BE)
7
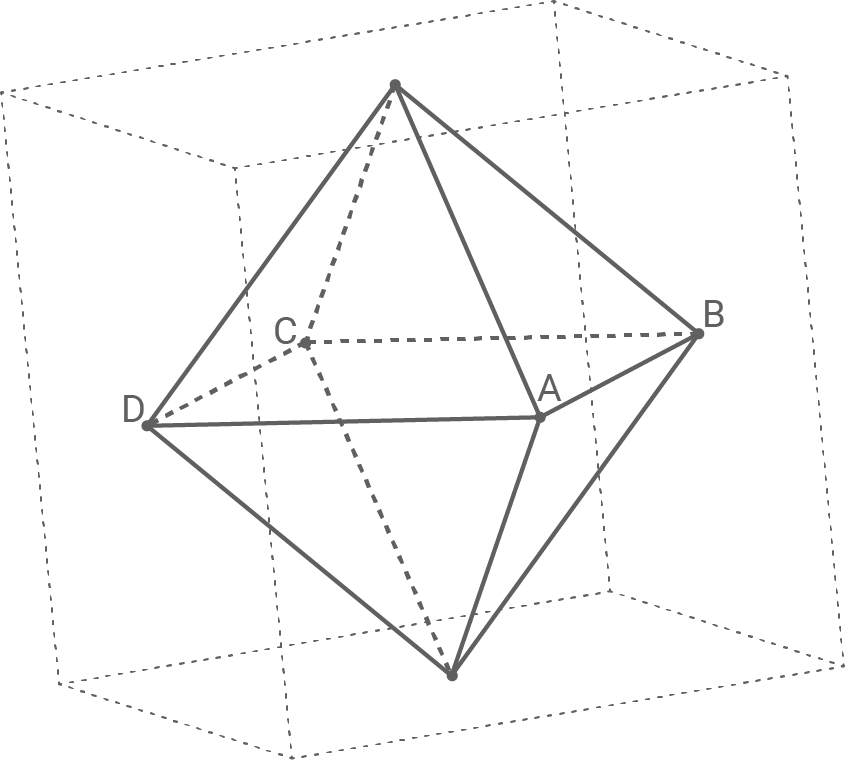
Die Mittelpunkte der Seitenflächen eines Würfels sind die Eckpunkte eines Oktaeders (vgl. Abbildung). Die Eckpunkte 

 und
und  des Oktaeders liegen in der Ebene
des Oktaeders liegen in der Ebene  mit der Gleichung
mit der Gleichung 

a)
Weise nach, dass die Kantenlänge des Würfels 12 beträgt.
(2 BE)
b)
Bestimme die Koordinaten eines der beiden Eckpunkte des Oktaeders, die nicht in  liegen.
liegen.
(3 BE)
8
Gegeben ist die Schar der Geraden  mit
mit 
a)
Begründe, dass alle Geraden der Schar parallel zueinander sind.
(1 BE)
b)
Betrachtet wird das Quadrat mit folgenden Eigenschaften:
 und
und  keine benachbarten Eckpunkte dieses Quadrats sind.
keine benachbarten Eckpunkte dieses Quadrats sind.
- Die Punkte
und
sind Eckpunkte des Quadrats.
- Zwei Seiten des Quadrats liegen auf Geraden der Schar.
(4 BE)
9
Die drei nicht sichtbaren Seiten des abgebildeten Würfels sollen jeweils mit einer der Zahlen  oder
oder  beschriftet werden. Dabei können Zahlen auch mehrfach verwendet werden.
Nach der Beschriftung soll der Würfel folgende Eigenschaften haben:
beschriftet werden. Dabei können Zahlen auch mehrfach verwendet werden.
Nach der Beschriftung soll der Würfel folgende Eigenschaften haben:
- Beim einmaligen Werfen ist der Erwartungswert für die erzielte Zahl gleich
- Auf den sechs Seiten des Würfels kommen genau drei verschiedene Zahlen vor.
- Die Wahrscheinlichkeit dafür, dass beim zweimaligen Werfen des Würfels zweimal die gleiche Zahl erzielt wird, beträgt

(5 BE)
10
Betrachtet wird ein Tetraeder, bei dem die Seiten mit den Zahlen  bis
bis  durchnummeriert sind. Beim Werfen des Tetraeders werden alle Zahlen mit gleicher Wahrscheinlichkeit erzielt. Das Tetraeder wird viermal geworfen. Die Zufallsgröße
durchnummeriert sind. Beim Werfen des Tetraeders werden alle Zahlen mit gleicher Wahrscheinlichkeit erzielt. Das Tetraeder wird viermal geworfen. Die Zufallsgröße  beschreibt die Anzahl der Würfe, bei denen die Zahl
beschreibt die Anzahl der Würfe, bei denen die Zahl  erzielt wird. Die Wahrscheinlichkeitsverteilung von
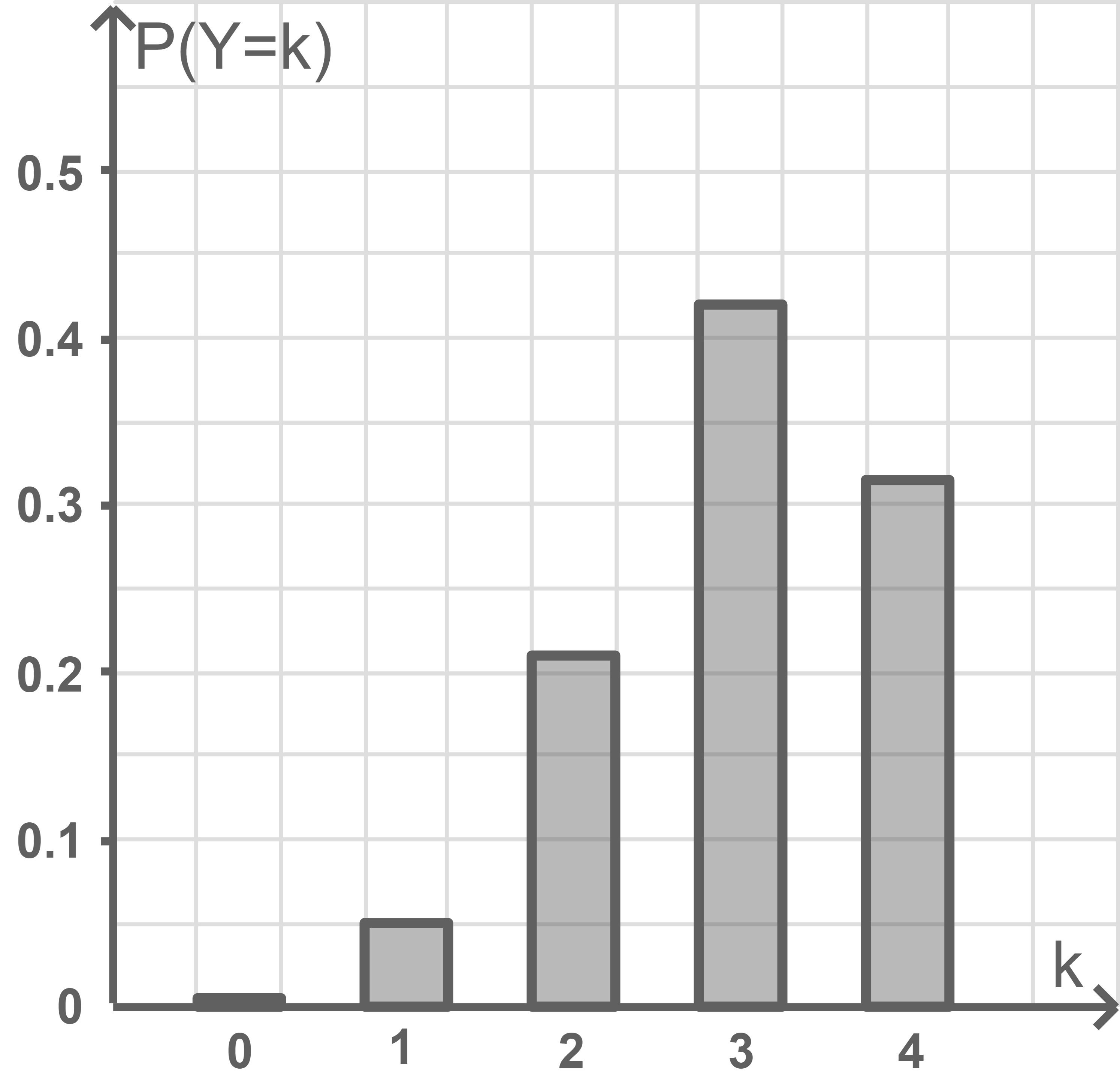
erzielt wird. Die Wahrscheinlichkeitsverteilung von  ist in Abbildung 1 dargestellt.
ist in Abbildung 1 dargestellt.
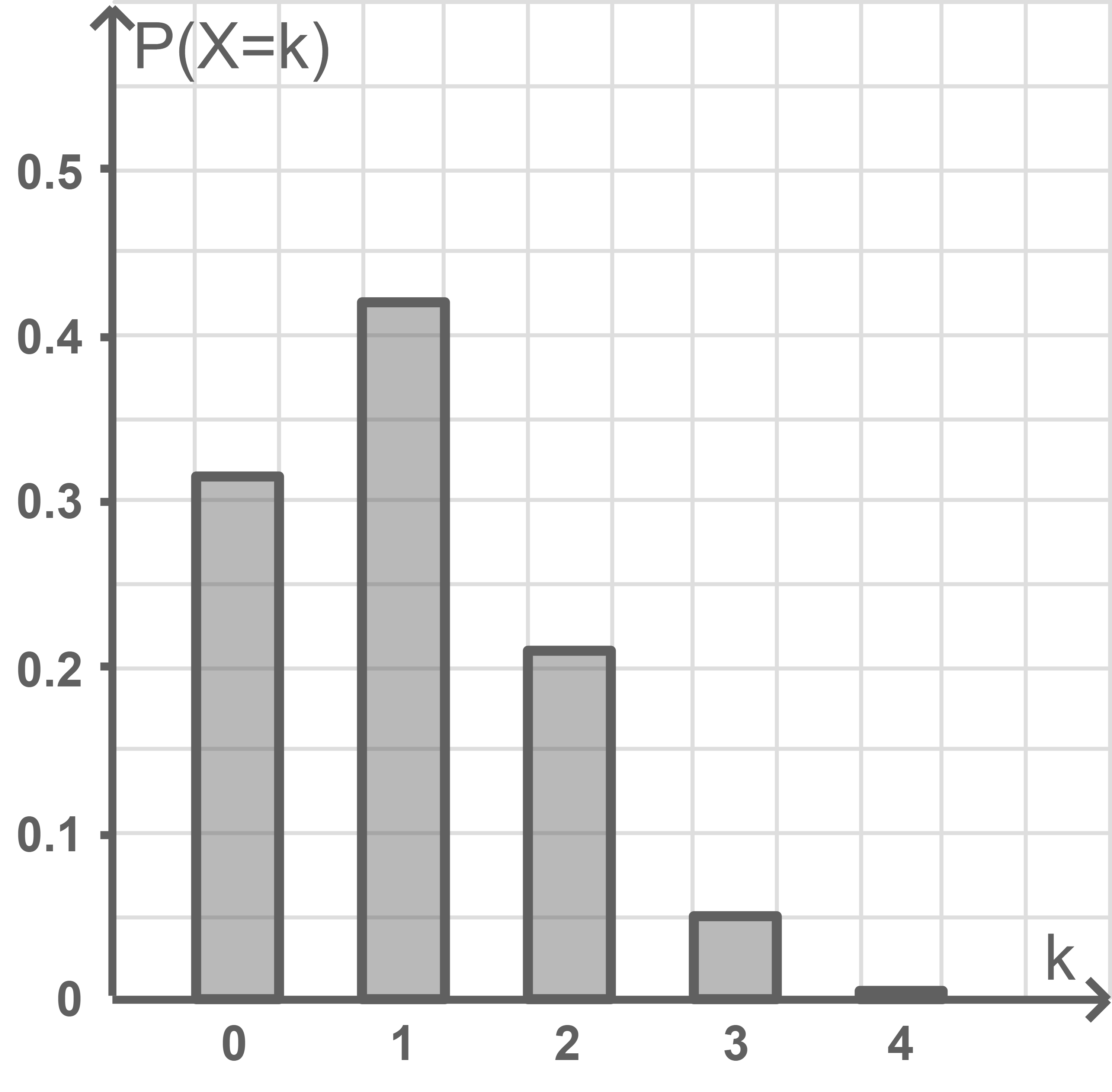

Abb. 1

Abb. 2
a)
Die Zufallsgröße  gibt die Anzahl der Würfe an, bei denen die Zahl
gibt die Anzahl der Würfe an, bei denen die Zahl  nicht erzielt wird. Stelle die Wahrscheinlichkeitsverteilung von
nicht erzielt wird. Stelle die Wahrscheinlichkeitsverteilung von  in Abbildung 2 dar.
in Abbildung 2 dar.
(2 BE)
b)
Bei einem anderen Zufallsexperiment werden ein roter und ein grüner Würfel, bei denen die Seiten jeweils mit den Zahlen  bis
bis  durchnummeriert sind, viermal gleichzeitig geworfen. Gib zu diesem Zufallsexperiment eine Zufallsgröße
durchnummeriert sind, viermal gleichzeitig geworfen. Gib zu diesem Zufallsexperiment eine Zufallsgröße  an, die die gleiche Wahrscheinlichkeitsverteilung hat wie
an, die die gleiche Wahrscheinlichkeitsverteilung hat wie  und begründe deine Angabe.
und begründe deine Angabe.
(3 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
5
a)
Die Tangente  gegeben durch die Gleichung
gegeben durch die Gleichung  hat eine positive Steigung, einen
hat eine positive Steigung, einen  -Achsenabschnitt von
-Achsenabschnitt von  und schneidet die
und schneidet die  -Achse bei
-Achse bei  Für die Steigung
Für die Steigung  folgt somit:
folgt somit:
 Somit ergibt sich die Gleichung
Somit ergibt sich die Gleichung 
b)
Die allgemeine Gleichung der Tangente ist gegeben durch  Für die Ableitung von
Für die Ableitung von  gilt:
gilt:
 Somit folgt
Somit folgt  und
und  Einsetzen der Koordinaten des Punktes, an dem die Tangente den Graphen berührt, in die Gleichung der Tangente liefert somit:
Einsetzen der Koordinaten des Punktes, an dem die Tangente den Graphen berührt, in die Gleichung der Tangente liefert somit:
![\(\begin{array}[t]{rll}
au^2&=&2au\cdot u + n &\quad \scriptsize \mid\;-2au^2 \\[5pt]
-au^2&=&n
\end{array}\)](https://mathjax.schullv.de/44a4ad57a45dd167f04ea978fd94c00489735b922770bc597fb9b365754582e7?color=5a5a5a) Somit gilt
Somit gilt  und die Tangente schneidet die
und die Tangente schneidet die  -Achse damit im Punkt
-Achse damit im Punkt 
6
Rechteck skizzieren
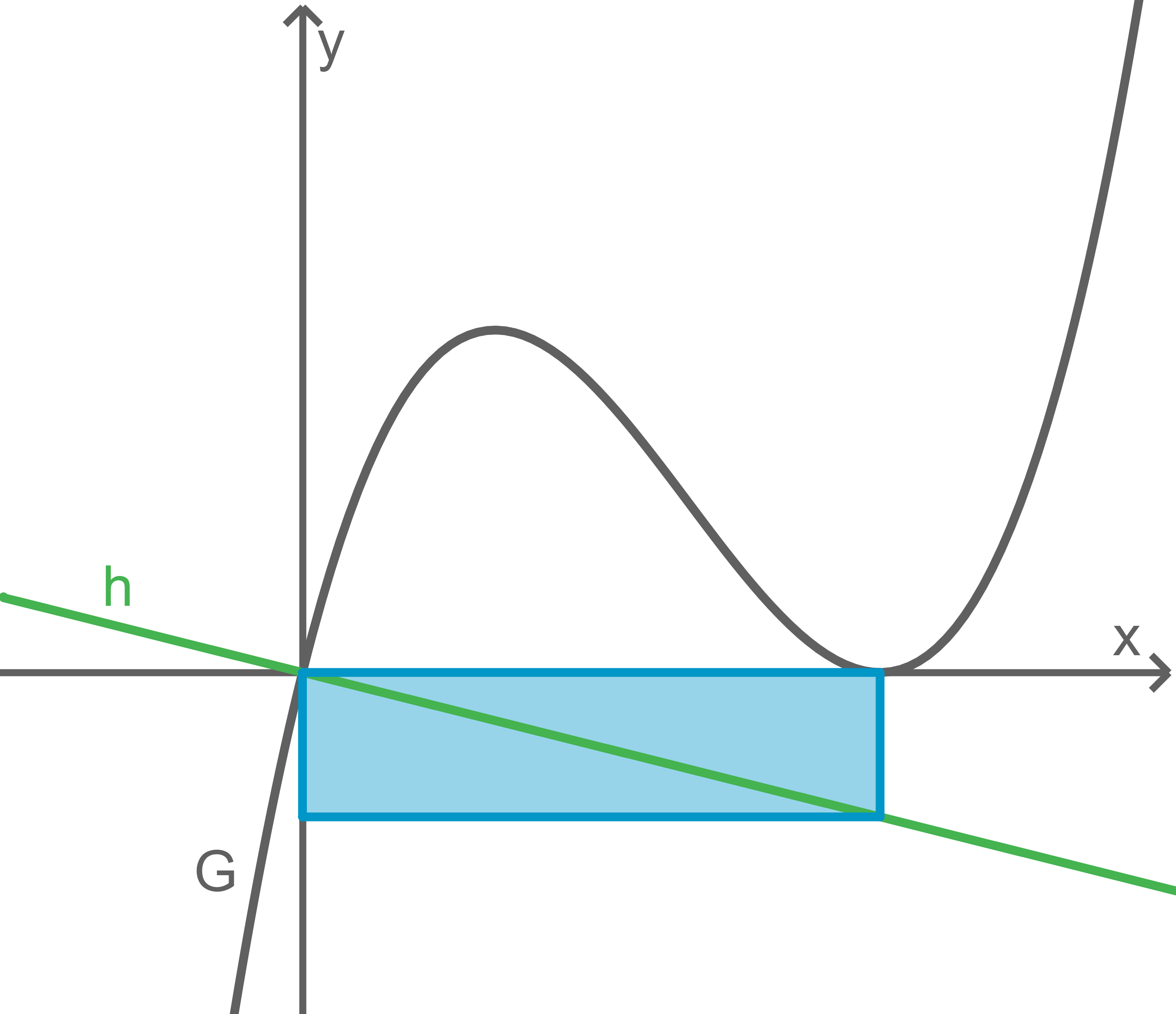 Unabhängigkeit des Flächeninhalts zeigen
Die Länge der Seite des Rechtecks, die auf der
Unabhängigkeit des Flächeninhalts zeigen
Die Länge der Seite des Rechtecks, die auf der  -Achse verläuft, ergibt sich durch die Differenz der
-Achse verläuft, ergibt sich durch die Differenz der  -Werte der beiden Punkte, in denen
-Werte der beiden Punkte, in denen  die
die  -Achse berührt, als
-Achse berührt, als  Für die Ableitung der Funktion
Für die Ableitung der Funktion  gilt:
gilt:
 Da
Da  senkrecht zur Tangente an
senkrecht zur Tangente an  im Koordinatenursprung verläuft, ergibt sich mit Hilfe von
im Koordinatenursprung verläuft, ergibt sich mit Hilfe von  die Steigung von
die Steigung von  als
als  Somit folgt
Somit folgt  Für die Länge der kürzeren Rechteckseite folgt damit:
Für die Länge der kürzeren Rechteckseite folgt damit:
 Damit folgt für den Flächeninhalt
Damit folgt für den Flächeninhalt  des Rechtecks
des Rechtecks  womit dieser unabhängig von
womit dieser unabhängig von  ist.
ist.

7
a)
b)
Der Ortsvektor des Mittelpunkts  der Strecke
der Strecke  ergibt sich wie folgt:
ergibt sich wie folgt:
![\(\begin{array}[t]{rll}
\overrightarrow{OM}&=&\overrightarrow{OA}+\dfrac{1}{2}\cdot\overrightarrow{AC} \\[5pt]
&=&\pmatrix{1\\2\\1}+\dfrac{1}{2}\cdot\pmatrix{-4\\-8\\8} \\[5pt]
&=&\pmatrix{-1\\-2\\5}
\end{array}\)](https://mathjax.schullv.de/f13901135af0ed1192f659481eb360c4523f0a812f6d7c78db8b4d46d714bd89?color=5a5a5a) Aus der Ebenengleichung von
Aus der Ebenengleichung von  lässt sich zudem der folgende Normalenvektor ablesen:
lässt sich zudem der folgende Normalenvektor ablesen:
 Es gilt
Es gilt 
 Da die Kantenlänge des Würfels
Da die Kantenlänge des Würfels  beträgt, ist der Abstand des gesuchten Eckpunktes des Oktaeders zu
beträgt, ist der Abstand des gesuchten Eckpunktes des Oktaeders zu  durch
durch  gegeben. Ein möglicher Ortsvektor ergibt sich somit als:
gegeben. Ein möglicher Ortsvektor ergibt sich somit als:
![\(\begin{array}[t]{rll}
\overrightarrow{OM}+2\cdot\overrightarrow{n}&=&\pmatrix{-1\\-2\\5}+2\cdot\pmatrix{2\\1\\2} \\[5pt]
&=&\pmatrix{3\\0\\9}
\end{array}\)](https://mathjax.schullv.de/04ec95577f1efba0c8c2541cc42cf6b5b46ccc1848f3bfc031c3117bb2f34c68?color=5a5a5a) Mögliche Koordinaten für den gesuchten Punkt sind somit gegeben durch
Mögliche Koordinaten für den gesuchten Punkt sind somit gegeben durch 
8
a)
Der Richtungsvektor der Geradenschar hängt nicht von  ab, somit sind alle Geraden der Schar parallel zueinander.
ab, somit sind alle Geraden der Schar parallel zueinander.
b)
Falls die Punkte  und
und  benachbarte Eckpunkte wären, könnten sie entweder auf der gleichen Geraden der Geradenschar liegen, oder auf zwei unterschiedlichen. In ersten Fall muss
benachbarte Eckpunkte wären, könnten sie entweder auf der gleichen Geraden der Geradenschar liegen, oder auf zwei unterschiedlichen. In ersten Fall muss  ein Vielfaches von dem Richtungsvektor der Geradenschar sein. Das liefert folgendes Gleichungssystem:
ein Vielfaches von dem Richtungsvektor der Geradenschar sein. Das liefert folgendes Gleichungssystem:
 Einsetzen der Lösung
Einsetzen der Lösung  aus Gleichung
aus Gleichung  in Gleichung
in Gleichung  ergibt
ergibt  was einen Widerspruch liefert. Somit besitzt das Gleichungssystem keine Lösung, das heißt
was einen Widerspruch liefert. Somit besitzt das Gleichungssystem keine Lösung, das heißt  und
und  sind keine benachbarten Eckpunkte, die auf derselben Gerade der Schar liegen.
Im zweiten Fall muss
sind keine benachbarten Eckpunkte, die auf derselben Gerade der Schar liegen.
Im zweiten Fall muss  orthogonal zum Richtungsvektor der Geradenschar liegen. Überprüfen ergibt:
orthogonal zum Richtungsvektor der Geradenschar liegen. Überprüfen ergibt:
![\(\begin{array}[t]{rll}
\pmatrix{11\\4\\5}\circ\pmatrix{4\\8\\1}&=&11\cdot4+4\cdot8+5\cdot1 \\[5pt]
&=&44+32+5 \\[5pt]
&=&81\neq 0
\end{array}\)](https://mathjax.schullv.de/8c7ea1de65e14214aec59d9ebba573a50ae84afc4feda83b6b6da37f55d1d57d?color=5a5a5a) Somit sind
Somit sind  und
und  auch keine benachbarten Eckpunkte, die auf verschiedenen Geraden der Schar liegen. Damit können
auch keine benachbarten Eckpunkte, die auf verschiedenen Geraden der Schar liegen. Damit können  und
und  insgesamt keine benachbarten Eckpunkte des Quadrats sein.
insgesamt keine benachbarten Eckpunkte des Quadrats sein.
9
Da jede Seite mit der gleichen Wahrscheinlichkeit gewürfelt wird, folgt mit Hilfe des Erwartungswerts  für die Summe
für die Summe  der Zahlen auf den drei nicht sichtbaren Seiten des Würfels:
Die Zahlen
der Zahlen auf den drei nicht sichtbaren Seiten des Würfels:
Die Zahlen  und
und  ergeben zusammen
ergeben zusammen  und erfüllen auch die zweite Bedingung. Für die Wahrscheinlichkeit, dass beim zweimaligen Werfen des Würfels zweimal die gleiche Zahl erzielt wird, folgt in diesem Fall:
und erfüllen auch die zweite Bedingung. Für die Wahrscheinlichkeit, dass beim zweimaligen Werfen des Würfels zweimal die gleiche Zahl erzielt wird, folgt in diesem Fall:
 Somit ist für diese Beschriftung der restlichen drei Seiten auch die dritte Bedingung erfüllt.
Somit ist für diese Beschriftung der restlichen drei Seiten auch die dritte Bedingung erfüllt.
10
a)
b)
Zufallsgröße angeben

 mögliche Ergebnisse, die alle gleich wahrscheinlich sind. Die Ergebnisse, bei denen keine der beiden Zahlen größer als
mögliche Ergebnisse, die alle gleich wahrscheinlich sind. Die Ergebnisse, bei denen keine der beiden Zahlen größer als  ist, ergeben sich wie folgt:
ist, ergeben sich wie folgt:

 Die Wahscheinlichkeit, bei einmaligem Würfeln keine Zahl zu erzielen, die größer als
Die Wahscheinlichkeit, bei einmaligem Würfeln keine Zahl zu erzielen, die größer als  ist, ergibt sich somit zu
ist, ergibt sich somit zu  Die Zufallsgrößen
Die Zufallsgrößen  und
und  sind somit beide binomialverteilt mit
sind somit beide binomialverteilt mit  und
und  das heißt sie besitzen die gleiche Wahrscheinlichkeitsverteilung.
das heißt sie besitzen die gleiche Wahrscheinlichkeitsverteilung.
Anzahl der Würfe, bei denen keine der beiden gewürfelten Zahlen größer als  ist.
ist.
Angabe begründen
Beim einmaligen Werfen der beiden Würfel gibt es insgesamt