Teil A
1
Gib in der Tabelle je eine zugehörige Funktionsgleichung an.
| Funktionsgleichung von |
Funktionsgleichung von |
|---|---|
(5 BE)
2
Gegeben ist die Funktion  durch
durch  mit
mit  .
.
a)
Skizziere den Graphen von 
Berechne den Inhalt der Fläche, den der Graph von mit der
mit der  -Achse im Intervall
-Achse im Intervall  vollständig begrenzt.
vollständig begrenzt.
Berechne den Inhalt der Fläche, den der Graph von
(3 BE)
b)
Alle Ursprungsgeraden mit positivem Anstieg haben mit dem Graphen von  im Intevall
im Intevall  gemeinsame Punkte.
Gib die Anzahl der gemeinsamen Punkte in Abhängigkeit vom Anstieg der Ursprungsgeraden an.
gemeinsame Punkte.
Gib die Anzahl der gemeinsamen Punkte in Abhängigkeit vom Anstieg der Ursprungsgeraden an.
(2 BE)
3
Gegeben sind die Funktion  mit
mit  sowie die Scharen der Funktionen
sowie die Scharen der Funktionen  mit
mit  und
und  mit
mit 
a)
Begründe, dass jede Funktion  die Nullstellen
die Nullstellen  und
und  besitzt.
besitzt.
(2 BE)
b)
Es gibt einen Wert von  , sodass der Graph von
, sodass der Graph von  in einem Schnittpunkt mit der
in einem Schnittpunkt mit der  -Achse die Tangente mit
-Achse die Tangente mit  besitzt.
besitzt.
Berechne diesen Wert für .
.
Berechne diesen Wert für
(3 BE)
4
Dargestellt sind Graphen der Schar  mit
mit  für zwei Werte
für zwei Werte  und
und 
 sowie die Asymptote
sowie die Asymptote  .
.
Die Graphen der Schar schneiden die
schneiden die  -Achse im Punkt
-Achse im Punkt  .
.
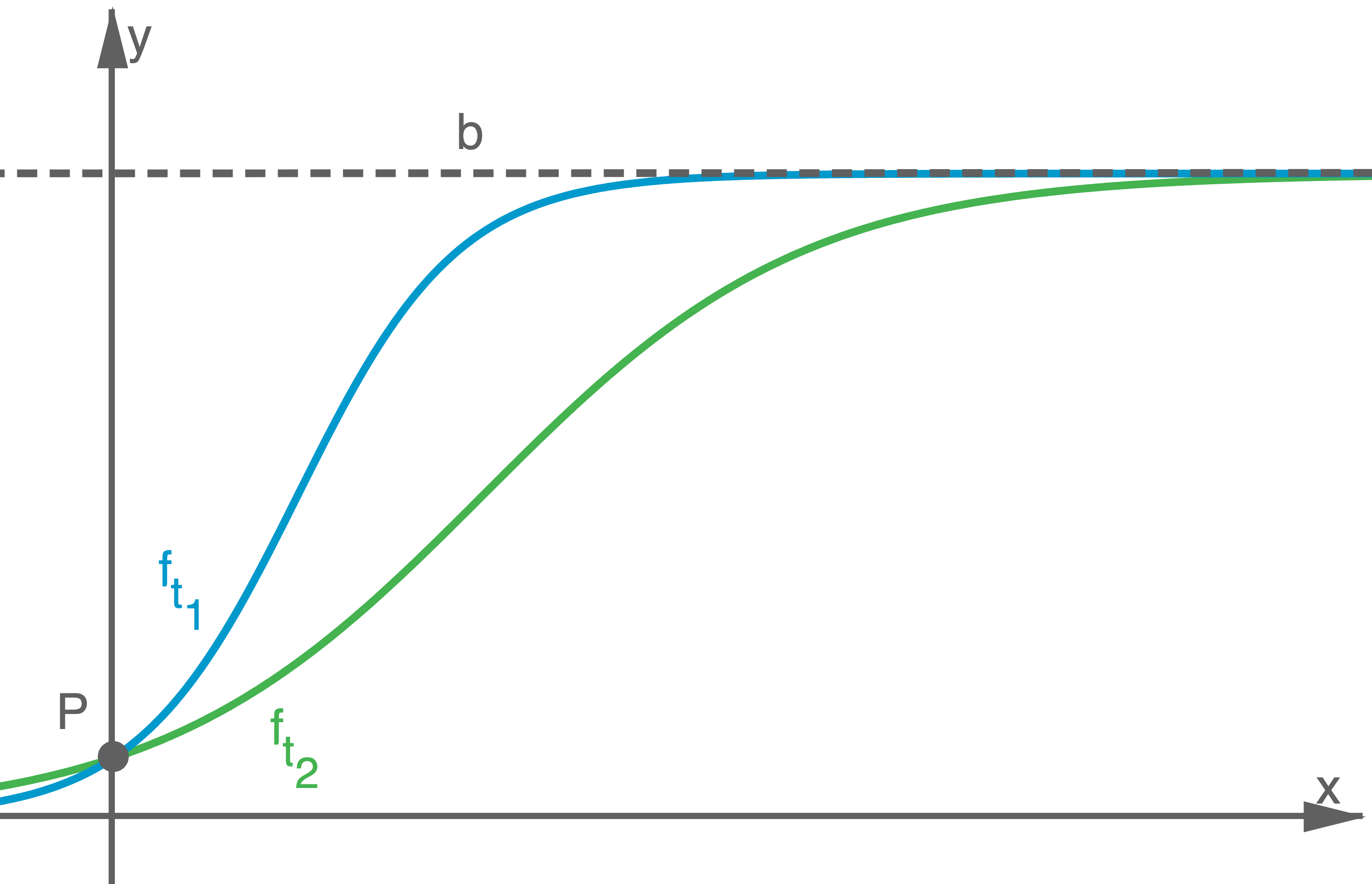
Die Graphen der Schar

a)
Gib die Werte von  und
und  an.
an.
(2 BE)
b)
Jeder Graph von  besitzt einen Wendepunkt
besitzt einen Wendepunkt 
Trage jeweils das richtige Relationszeichen ein.
Trage jeweils das richtige Relationszeichen ein.
|
|
|||
|
|
|||
|
|
(3 BE)
5
Gegeben ist das Dreieck  mit
mit  und
und  .
.
a)
Berechne die Länge der Seitenhalbierenden vom Eckpunkt  zur Seite
zur Seite 
(3 BE)
b)
Bei Spiegelung von  am Mittelpunkt der Seite
am Mittelpunkt der Seite  entsteht der Bildpunkt
entsteht der Bildpunkt  .
.
Ermittle die Koordinaten von .
.
Ermittle die Koordinaten von
(2 BE)
6
Für jede reelle Zahl  sind die Vektoren
sind die Vektoren  und
und  gegeben.
gegeben.
a)
Berechne die Werte für  so, dass die Vektoren
so, dass die Vektoren  und
und  orthogonal zueinander sind.
orthogonal zueinander sind.
(3 BE)
b)
Der Koordinatenursprung und die Vektoren  und
und  erzeugen für jedes
erzeugen für jedes  eine Ebene
eine Ebene  .
.
Ermittle den Wert für so, dass
so, dass  die
die  -Ebene ist.
-Ebene ist.
Ermittle den Wert für
(2 BE)
7
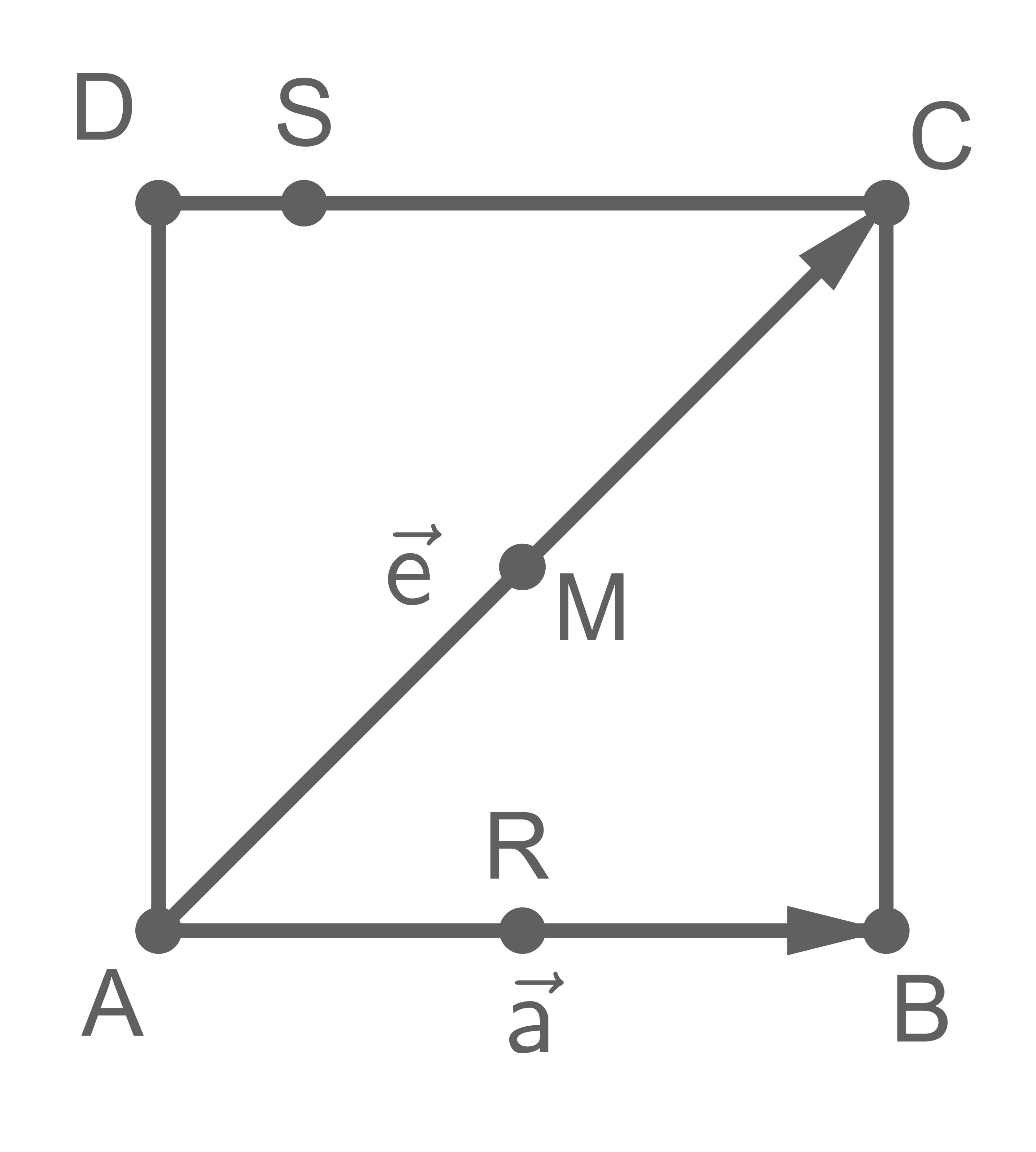
Der Punkt  ist Schnittpunkt der Diagonalen eines Quadrates
ist Schnittpunkt der Diagonalen eines Quadrates  mit
mit  und
und  .
.
Der Punkt ist der Mittelpunkt der Seite
ist der Mittelpunkt der Seite 
Auf der Seite liegt ein Punkt
liegt ein Punkt  , der diese Seite im Verhältnis
, der diese Seite im Verhältnis  teilt.
teilt.
Der Punkt
Auf der Seite
a)
Stelle den Sachverhalt graphisch dar.
(2 BE)
b)
Gib die folgenden Vektoren nur unter Verwendung der Vektoren  und
und  an.
an.



(3 BE)
8
In einem Restaurant wird ein Drei-Gänge-Menü gereicht. Erfahrungsgemäß wählen von 100 Gästen 60 keine Vorspeise, 40 verzichten auf die Nachspeise und 20 wählen weder Vorspeise noch Nachspeise. Alle Gäste wählen den Hauptgang.
a)
Vervollständige folgende Vierfeldertafel.
| Gesamt | |||
|---|---|---|---|
| Gesamt |
Vorspeise  Nachspeise
Nachspeise 
(2 BE)
b)
Gib die Anzahl der Gäste an, die alle drei Gänge wählen.
(1 BE)
c)
Berechne die Wahrscheinlichkeit dafür, dass ein Gast, der keine Vorspeise wählt, auch auf die Nachspeise verzichtet.
(2 BE)
9
Die Füllmenge einer Abfüllmaschine für Milch wird normalverteilt mit einem Erwartungswert von  und einer Standardabweichung von
und einer Standardabweichung von  modelliert.
Die Gleichung der Dichtefunktion einer Normalverteilung ist
modelliert.
Die Gleichung der Dichtefunktion einer Normalverteilung ist  .
.
a)
Gegeben sind die Dichtefunktionen 

 durch:
durch:
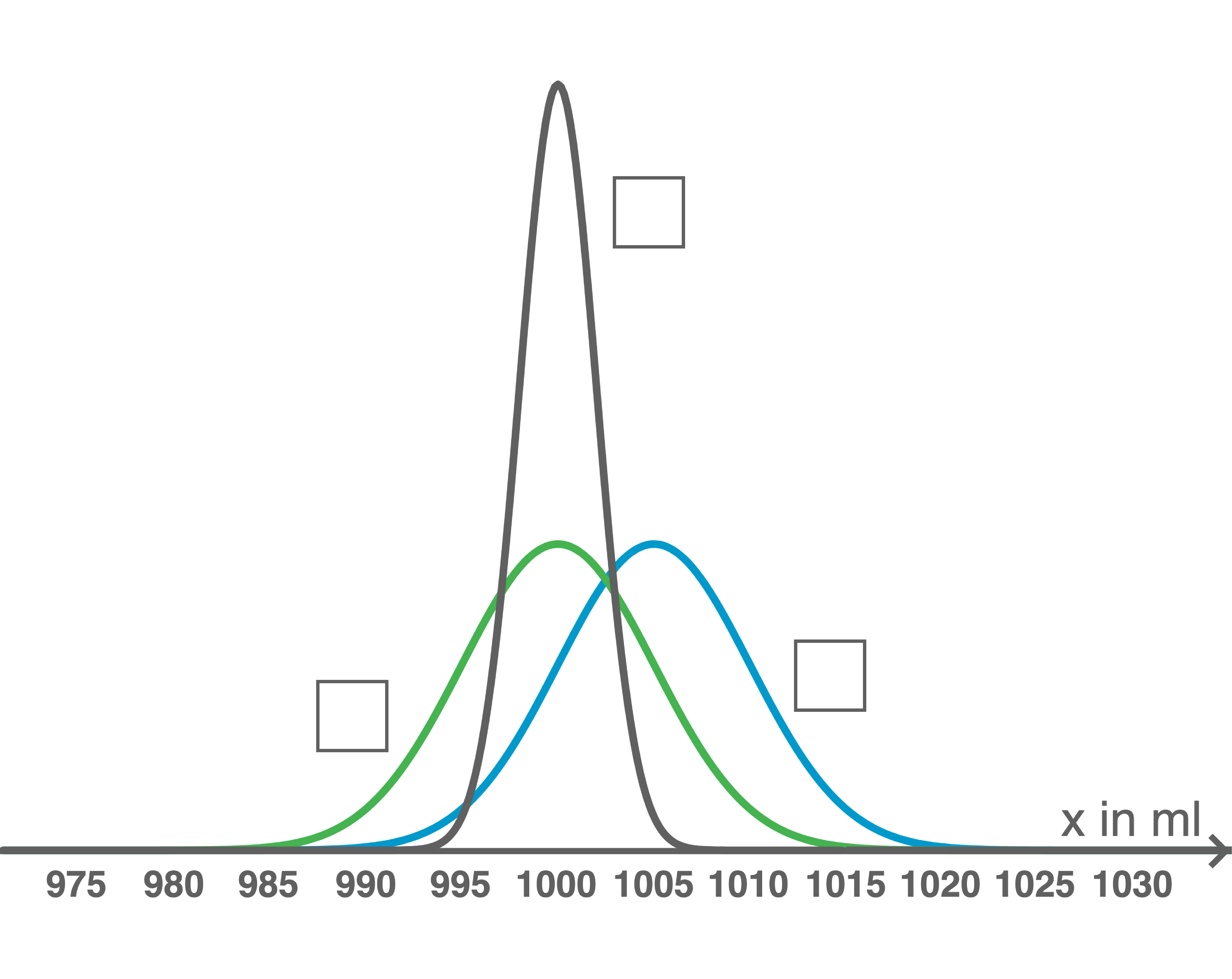 Kreuze die Gleichung an, die den obigen Sachverhalt korrekt beschreibt.
Kreuze die Gleichung an, die den obigen Sachverhalt korrekt beschreibt.
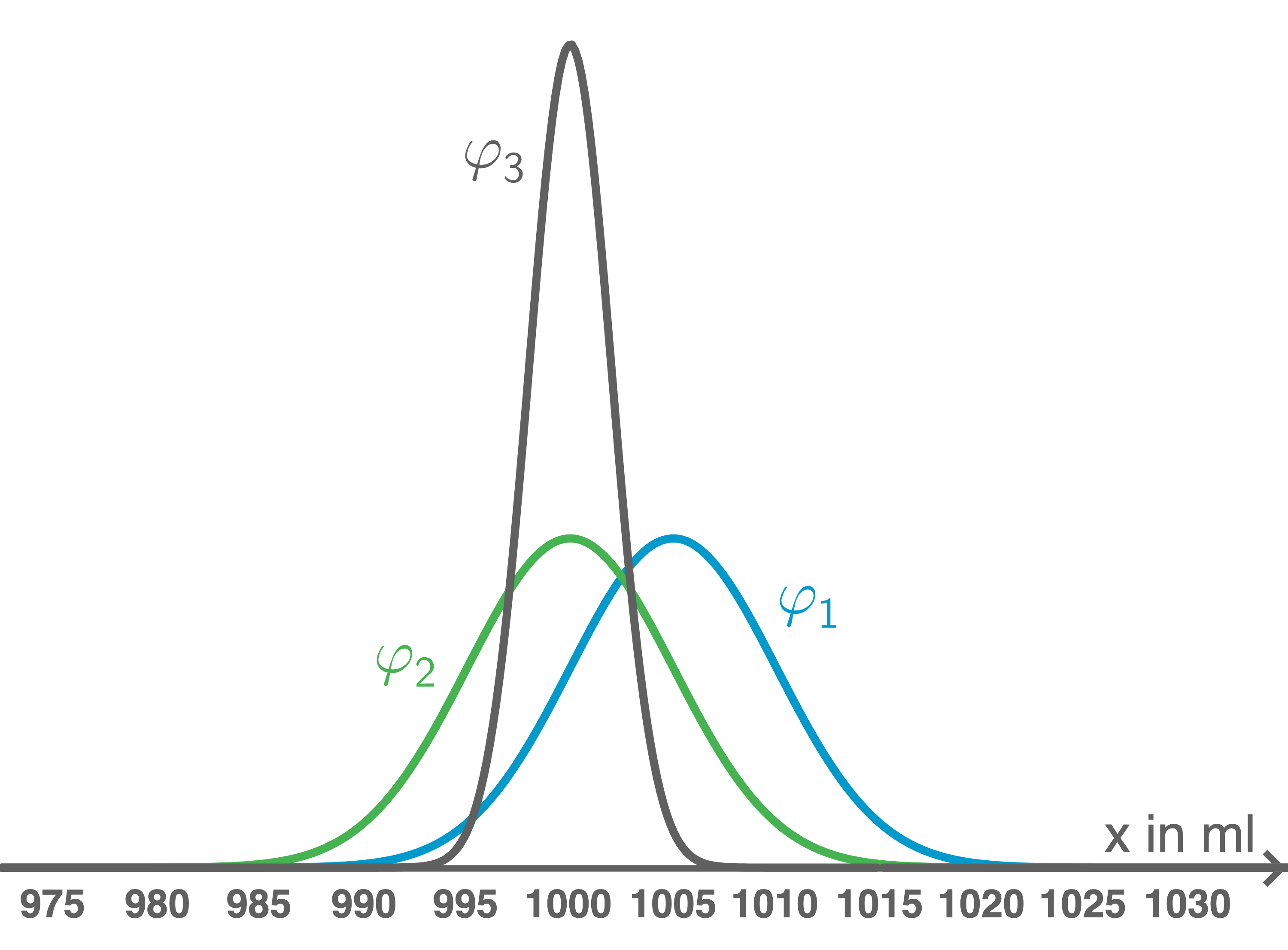
Ordne jedem Graphen die zugehörige Dichtefunktion zu.
|
|
||
|
|
||
|
|

Ordne jedem Graphen die zugehörige Dichtefunktion zu.
(3 BE)
b)
Gib die  -Umgebung um den Erwartungswert an.
-Umgebung um den Erwartungswert an.
Beschreibe deren Bedeutung im Sachzusammenhang.
Beschreibe deren Bedeutung im Sachzusammenhang.
(2 BE)
10
Die Abbildung zeigt ein zweistufiges Baumdiagramm für die Ereignisse  und
und 
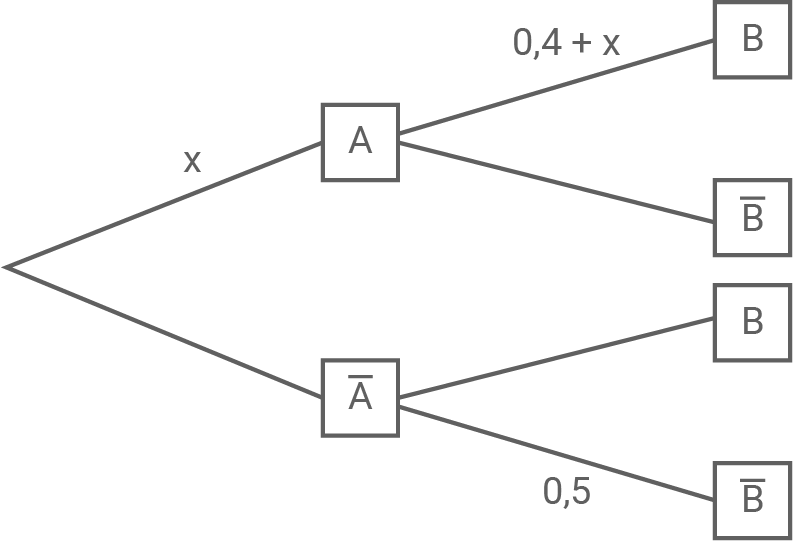

a)
Berechne für  die Wahrscheinlichkeit
die Wahrscheinlichkeit  .
.
(2 BE)
b)
Berechne  so, dass die Wahrscheinlichkeit
so, dass die Wahrscheinlichkeit  minimal wird.
minimal wird.
(3 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
2
a)
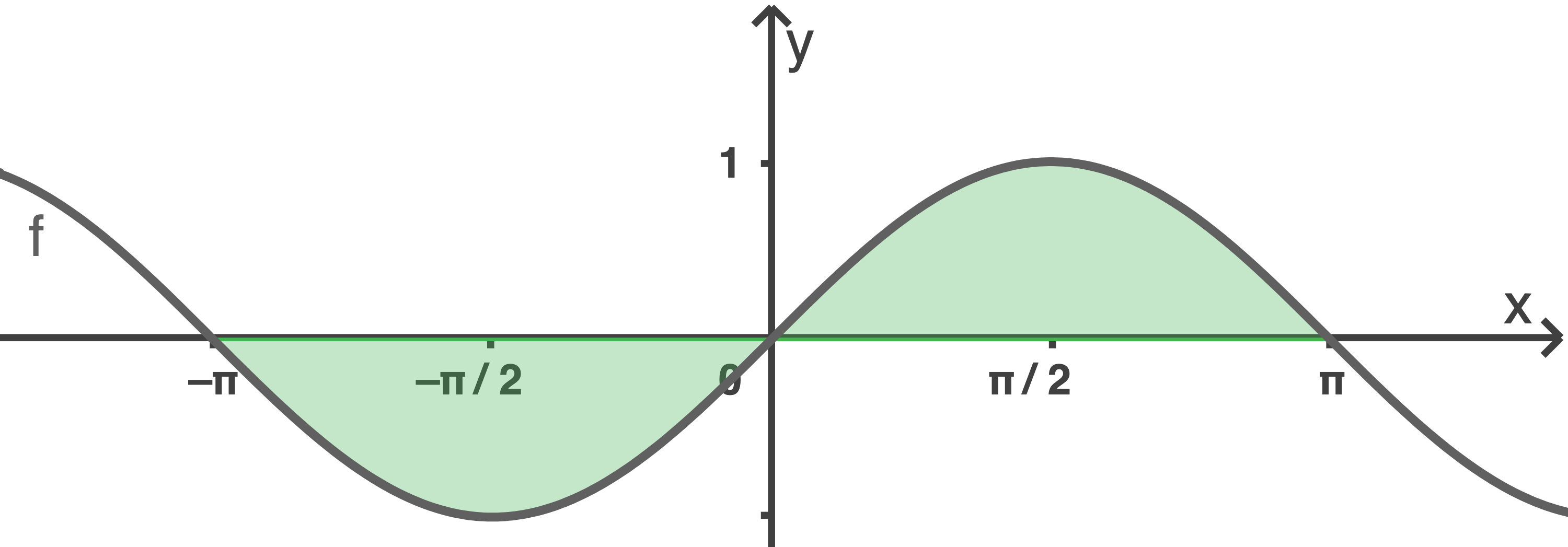
b)
Ist die Steigung der Ursprungsgerade größer oder gleich der Steigung der Tangente an  durch den Ursprung, so gibt es einen gemeinsamen Punkt. Für diese Steigung folgt:
durch den Ursprung, so gibt es einen gemeinsamen Punkt. Für diese Steigung folgt:
 Wenn die Steigung positiv und kleiner als
Wenn die Steigung positiv und kleiner als  ist, gibt es drei gemeinsame Punkte. Insgesamt gilt somit:
ist, gibt es drei gemeinsame Punkte. Insgesamt gilt somit:
ein gemeinsamer Punkt
drei gemeinsame Punkte
3
a)
Aufgrund des Satzes vom Nullprodukt genügt es, die Nullstellen der einzelnen Faktoren zu betrachten:
 also
also 
 also
also 
b)
Ausmultiplizieren der Funktionsgleichung und ableiten liefert:
 Die Steigung der Tangente kann als
Die Steigung der Tangente kann als  abgelesen werden und
abgelesen werden und  schneidet die
schneidet die  -Achse in
-Achse in  Einsetzen in
Einsetzen in  liefert:
liefert:
4
a)
b)
5
a)
b)
6
a)
b)
Allgemeine Ebenengleichung:  Damit
Damit  die
die  -Ebene ist, muss
-Ebene ist, muss  gelten.
Das ist für
gelten.
Das ist für  der Fall.
der Fall.
7
a)
b)
8
a)
| 20 | 40 | 60 | |
| 20 | 20 | 40 | |
| 40 | 60 | 100 |
b)
20 Gäste
c)
9
a)
Ankreuzen:  Zuordnungen:
Zuordnungen:

b)
Angeben: 990 ml bis 1010 ml
Beschreiben: Ca. 95 % der Abfüllmengen dieser Maschine liegen zwischen 990 ml und 1010 ml.
10
a)
b)