Teil C1
1
Gegeben sind die Punkte 
, 
, 
und 
.
Die Dreiecke
und 
sind Grund- und Deckfläche eines dreiseitigen Prismas. Die Strecke 
ist eine Seitenkante des Prismas.
Die Dreiecke
a)
Berechne den Flächeninhalt des Dreiecks .
Ermittle den Abstand des Punktes
von der Geraden durch die Punkte 
und 
Ermittle den Abstand des Punktes
(4 BE)
b)
Zeige, dass die Seitenkante senkrecht auf der Fläche steht.
(1 BE)
c)
Bestimme die Koordinaten der Punkte 
und 
.
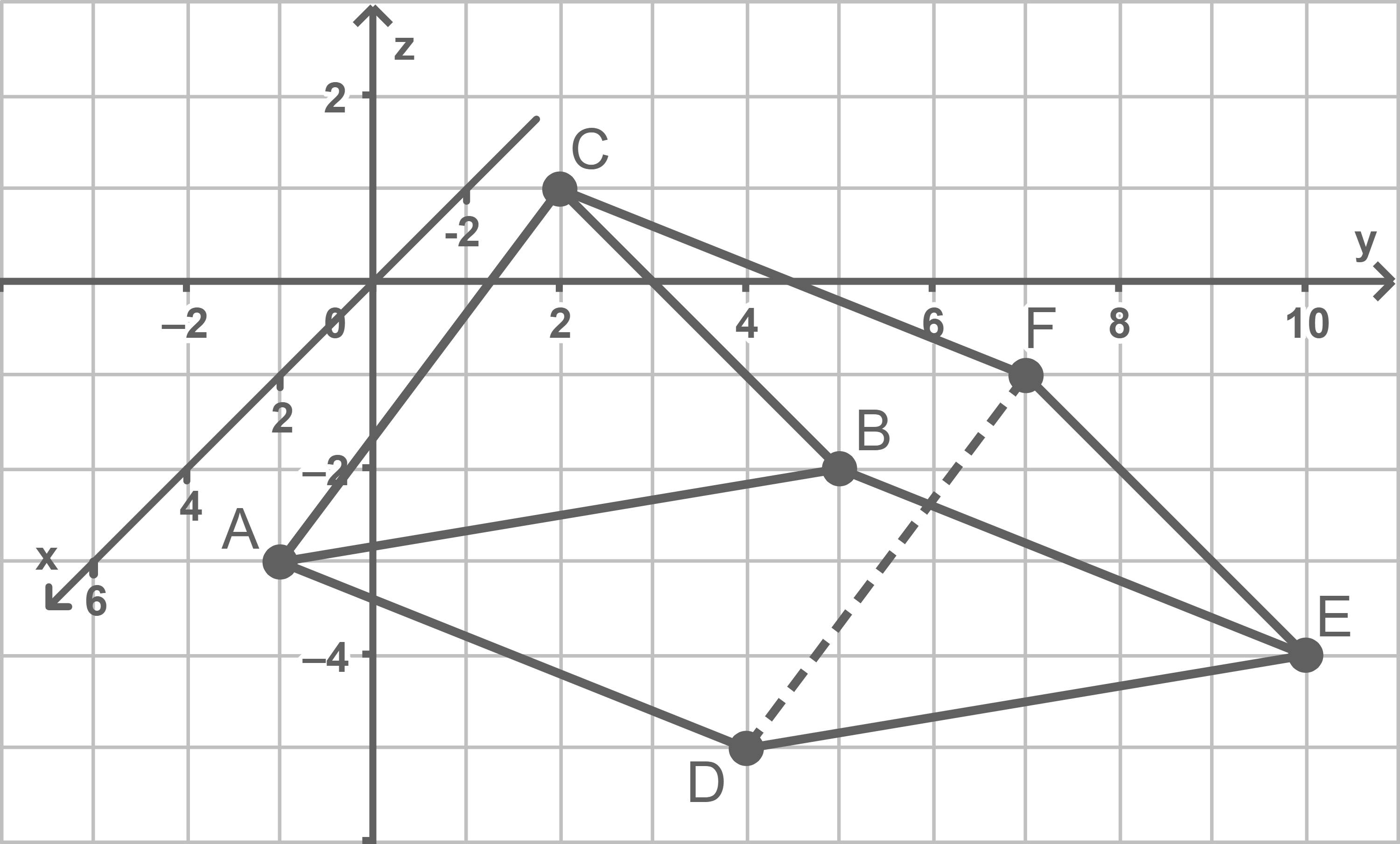
Stelle das Prisma in einem rechtwinkligen Koordinatensystem dar.
Beschreibe eine Möglichkeit für das Zerlegen des Prismas in zwei volumengleiche Teilkörper.
Stelle das Prisma in einem rechtwinkligen Koordinatensystem dar.
Beschreibe eine Möglichkeit für das Zerlegen des Prismas in zwei volumengleiche Teilkörper.
(4 BE)
d)
Begründe ohne Rechnung, dass die Kante des Prismas die 
-
-Koordinatenebene schneidet.
Bestimme die Koordinaten dieses Schnittpunktes.
Bestimme die Koordinaten dieses Schnittpunktes.
(3 BE)
2
Im Jahr 2012 gab es in Deutschland 40,7 Millionen Haushalte. Das Statistische Bundesamt veröffentlichte für die verschiedenen Haushaltsgrößen folgende Zahlen:
Quelle: https://www.destatis.de (06.11.2014)
| Einpersonenhaushalte | 41 % |
|---|---|
| Zweipersonenhaushalte | 35 % |
| Dreipersonenhaushalte | 12 % |
| Haushalte mit vier und mehr Personen | 12 % |
a)
Für eine telefonische Befragung werden drei Haushalte zufällig ausgewählt.
Berechne die Wahrscheinlichkeit folgender Ereignisse:
Berechne die Wahrscheinlichkeit folgender Ereignisse:
„Ein Zweipersonenhaushalt, ein Dreipersonenhaushalt und ein Haushalt mit vier und mehr Personen werden ausgewählt.“
„In keinem der drei ausgewählten Haushalte leben mehr als zwei Personen.“
(2 BE)
b)
An einem Abend werden 56 zufällig ausgewählte Haushalte telefonisch befragt.
Ermittle unter Annahme des Modells der Binomialverteilung die Wahrscheinlichkeit folgender Ereignisse:
Ermittle unter Annahme des Modells der Binomialverteilung die Wahrscheinlichkeit folgender Ereignisse:
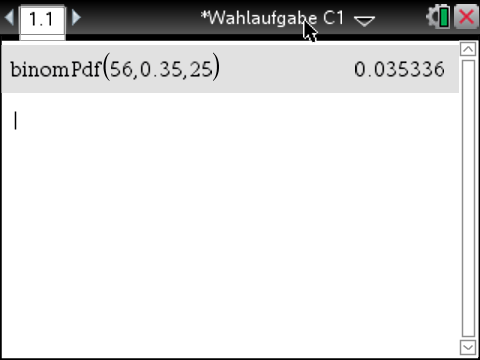
„Genau 25 Haushalte sind Zweipersonenhaushalte.“
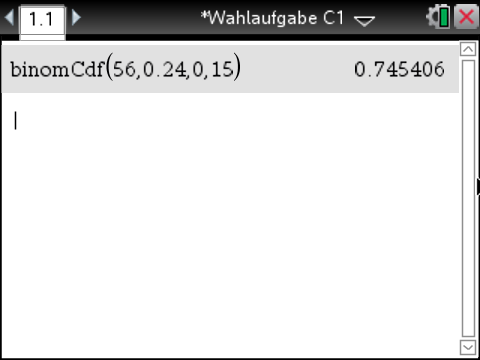
„In höchstens 15 der Haushalte leben mehr als zwei Personen.“
(2 BE)
c)
Bestimme die Anzahl der Haushalte, die mindestens befragt werden müssen, damit mit einer Wahrscheinlichkeit von mindestens 
mindestens zwei Haushalte mit vier oder mehr Personen dabei sind.
(2 BE)
d)
Aufgrund familienpolitischer Maßnahmen wird erwartet, dass im Zeitraum von 
Jahren die Zahl der Haushalte mit drei und mehr Personen auf 
ansteigt. Im Jahr 2022 könnte dazu ein Alternativtest durchgeführt werden, in dem 
zufällig ausgewählte Haushalte befragt werden. Sind unter diesen mehr als 
Drei- und Mehrpersonenhaushalte, so soll an die Wirksamkeit der familienpolitischen Maßnahmen geglaubt werden. Anderenfalls geht man weiterhin von 
Drei- und Mehrpersonenhaushalten aus.
Berechne die Wahrscheinlichkeiten für die Fehler erster und zweiter Art.
Berechne die Wahrscheinlichkeiten für die Fehler erster und zweiter Art.
(2 BE)
,
![\(\begin{array}[t]{rll}
\overrightarrow{AD} \circ \overrightarrow{AB}&=&\pmatrix{-8\\1\\-6}\circ\pmatrix{0\\6\\1} \\[5pt]
&=&0
\end{array}\)](https://mathjax.schullv.de/99e369c23dac54663bf0b48644208227777b5ee170fc6e13a837d9b6d1e583ea?color=5a5a5a)
![\(\begin{array}[t]{rll}
\overrightarrow{AD} \circ \overrightarrow{AC}&=&\pmatrix{-8\\1\\-6}\circ\pmatrix{-2\\2\\3} \\[5pt]
&=&0
\end{array}\)](https://mathjax.schullv.de/f978aef035577dd38202e0ded7229556f52aa71b9150537f5b66a526168633df?color=5a5a5a)
Der Vektor 
steht somit senkrecht auf den Spannvektoren der Ebene in der das Dreieck liegt und damit die Seitenkante senkrecht auf der Fläche 
Die Zufallsvariable 
die die Anzahl der Haushalte mit mehr als zwei Personen angibt, ist binomialverteilt mit den Parametern 
und 
1
a)
Flächeninhalt des Dreiecks 
berechnen
Für die Längen der Seiten 
und 
folgt mit Hilfe des CAS:
![\(\begin{array}[t]{rll}
\left\vert\overrightarrow{AB}\right\vert&=&\left\vert\pmatrix{6\\8\\1}-\pmatrix{6\\2\\0}\right\vert \\[5pt]
&=&\sqrt{37}\;[\text{LE}]
\end{array}\)](https://mathjax.schullv.de/04fdd175495175034a2b5727bcc69f398232c87c2f44cb2a1b26bff71f3ebc0c?color=5a5a5a)
![\(\begin{array}[t]{rll}
\left\vert\overrightarrow{AC}\right\vert&=&\left\vert\pmatrix{4\\4\\3}-\pmatrix{6\\2\\0}\right\vert \\[5pt]
&=&\sqrt{17}\;[\text{LE}]
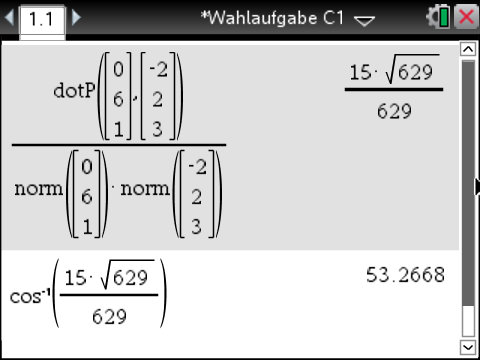
\end{array}\)](https://mathjax.schullv.de/bc1f02a2ae116a302a088bc118719b958792e9be94f1459bac9d27334cccda73?color=5a5a5a)
Für den eingeschlossenen Winkel 
zwischen den Seiten und gilt:
Mit Hilfe des solve-Befehls des CAS folgt:
Die Höhe 
des Dreiecks bezüglich der Grundseite ergibt sich somit mit dem CAS wie folgt:
![\(\begin{array}[t]{rll}
h&=&\left\vert\overrightarrow{AC}\right\vert\cdot\sin(\alpha) \\[5pt]
&\approx&3,3\;[\text{LE}]
\end{array}\)](https://mathjax.schullv.de/3f409e61b6aaaee5cff1282f498e5ac48ea44f9f6bde5015c0c10cad7889ebe4?color=5a5a5a)
Für den Flächeninhalt 
des Dreiecks folgt damit insgesamt:
![\(\begin{array}[t]{rll}
A_{ABC}&=&\dfrac{1}{2}\cdot\left\vert\overrightarrow{AB}\right\vert\cdot h \\[5pt]
&\approx&10\;[\text{FE}]
\end{array}\)](https://mathjax.schullv.de/439101113e1434a0c271a19a267da3502c2c96cb03b5013ebab30421813cd2a6?color=5a5a5a)
Abstand des Punktes 
ermitteln
Der Abstand des Punktes von der Geraden durch die Punkte und 
ist durch die oben berechnete Höhe gegeben und beträgt somit ca. 
b)
c)
Koordinaten bestimmen
Da die Kante senkrecht auf dem Dreieck steht, handelt es sich um ein gerades Prisma und es folgt mit dem CAS:
![\(\begin{array}[t]{rll}
\overrightarrow{OE}&=&\overrightarrow{OB}+\overrightarrow{AD} \\[5pt]
&=&\pmatrix{-2\\9\\-5}
\end{array}\)](https://mathjax.schullv.de/3ace8e88afad083e917103cb387c93b27bf2e1eeb7e6512d10fb45f4ec8c20d8?color=5a5a5a)
![\(\begin{array}[t]{rll}
\overrightarrow{OF}&=&\overrightarrow{OC}+\overrightarrow{AD} \\[5pt]
&=&\pmatrix{-4\\5\\-3}
\end{array}\)](https://mathjax.schullv.de/f61f400ff56d2438d3317174f879bef92ff4deaaeb1177bdd1169e6d2280f589?color=5a5a5a)
Prisma darstellen
Möglichkeit für das Zerlegen beschreiben
Die beiden Grundflächen und des Prismas sind gleichgroß. Somit entstehen zwei volumengleiche Teilkörper, indem das große Prisma entlang des durch die Mittelpunkte der drei Seitenkanten aufgespannten Dreiecks zerlegt wird.
d)
Begründen, dass 
die 
-
-Ebene schneidet
Die 
-Koordinaten der beiden Endpunkte und 
besitzen unterschiedliche Vorzeichen, somit schneidet die Kante die --Ebene.
Koordinaten des Schnittpunktes bestimmen
Die eindeutige Gerade 
durch die Punkte und besitzt folgende mögliche Geradengleichung:
Ein allgemeiner Punkt in der --Ebene besitzt die Koordinaten 
Gleichsetzen mit der Geradengleichung von liefert folgendes lineares Gleichungssystem:
Lösen dieses Gleichungssystems mit dem CAS liefert 
und 
Der gesuchte Schittpunkt besitzt somit die Koordinaten 
2
a)
Da die Reihenfolge, in der die Haushalte ausgewählt werden, keine Rolle spielt, ergeben sich 
verschiedene Möglichkeiten für das Ereignis und es folgt:
![\(\begin{array}[t]{rll}
P(A)&=&6\cdot0,35\cdot0,12\cdot0,12 \\[5pt]
&\approx&0,0302 \\[5pt]
&=&3,02\,\%
\end{array}\)](https://mathjax.schullv.de/388945835122b3cfc4f75db5af2efd82811bdea4639ef53d851b21abefc96246?color=5a5a5a)
Die Wahrscheinlichkeit für einen Haushalt mit 2 oder weniger Personen beträgt 
Für das Ereignis folgt somit:
![\(\begin{array}[t]{rll}
P(B)&=&0,76 \cdot 0,76 \cdot 0,76 \\[5pt]
&\approx&0,439 \\[5pt]
&=&43,9\,\%
\end{array}\)](https://mathjax.schullv.de/da2d12a305f076a979e2d4f70ab573a65a5d2a9472c18c57f41233c9967f64c4?color=5a5a5a)
b)
Die Zufallsvariable 
die die Anzahl der Zweipersonenhaushalte angibt, ist binomialverteilt mit den Parametern und 
Mit dem CAS folgt:
![\(\begin{array}[t]{rll}
P(C)&=&B_{56;0,35}(X=25) \\[5pt]
&\approx&0,0353 \\[5pt]
&=&3,53\,\%
\end{array}\)](https://mathjax.schullv.de/011f6f75fbf015a0692b6a212e35464f0e802ec419f4ad8b7e50e5fc14fefbd2?color=5a5a5a)
Mit dem CAS ergibt sich:
![\(\begin{array}[t]{rll}
P(C)&=&B_{56;0,24}(Y\leq15) \\[5pt]
&\approx&0,7454 \\[5pt]
&=&74,54\,\%
\end{array}\)](https://mathjax.schullv.de/b6f7cef733abf1c7819752d1c5e4e75245589ec01c72a2fd4f4fcb48b928e4f4?color=5a5a5a)
c)
Die Zufallsvariable 
die die Anzahl der Haushalte mit vier oder mehr Personen angibt, ist binomialverteiltmit mit unbekanntem 
und 
Mit der allgemeinen Formel der Binomialgleichung folgt:
Mit Hilfe des nsolve-Befehls des CAS folgt:
Es müssen somit mindestens 
Haushälte befragt werden, damit mit einer Wahrscheinlichkeit von mindestens mindestens zwei Haushalte mit vier oder mehr Personen darunter sind.
d)
Wahrscheinlichkeit für Fehler erster Art berechnen
Die Zufallsvariable 
die die Anzahl der Haushalte mit drei oder mehr Personen angibt, ist binomialverteilt mit den Parametern 
und 
Mit dem CAS folgt für die Wahrscheinlichkeit des Fehlers erster Art:
Wahrscheinlichkeit für Fehler zweiter Art berechnen
Die Zufallsvariable die die Anzahl der Haushalte mit drei oder mehr Personen angibt, ist nun binomialverteilt mit den Parametern und 
Mit dem CAS folgt für die Wahrscheinlichkeit des Fehlers zweiter Art somit:
![\(\begin{array}[t]{rll}
B_{100;0,30}(X\leq27)&\approx&0,2964 \\[5pt]
&=&29,64\,\%
\end{array}\)](https://mathjax.schullv.de/53ae66ddb782e21d539d52f0054c2a55d748a1ab7694e0a1131dccf89c9f32f8?color=5a5a5a)
,
Der Vektor steht somit senkrecht auf den Spannvektoren der Ebene in der das Dreieck liegt und damit die Seitenkante senkrecht auf der Fläche
1
a)
Flächeninhalt des Dreiecks berechnen
Für die Längen der Seiten und folgt mit Hilfe des CAS:
Die Höhe des Dreiecks bezüglich der Grundseite ergibt sich somit mit dem CAS wie folgt:
Für den Flächeninhalt des Dreiecks folgt damit insgesamt:
Abstand des Punktes ermitteln
Der Abstand des Punktes von der Geraden durch die Punkte und ist durch die oben berechnete Höhe gegeben und beträgt somit ca.
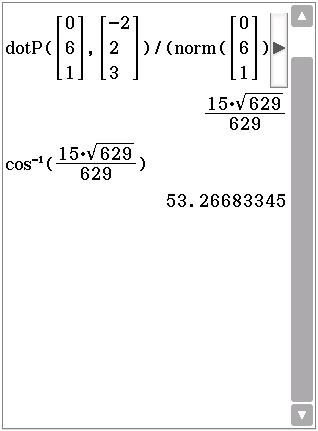
Für den eingeschlossenen Winkel zwischen den Seiten und gilt:
Mit Hilfe des solve-Befehls des CAS folgt:
b)
c)
Koordinaten bestimmen
Da die Kante senkrecht auf dem Dreieck steht, handelt es sich um ein gerades Prisma und es folgt mit dem CAS:
Prisma darstellen
Möglichkeit für das Zerlegen beschreiben
Die beiden Grundflächen und des Prismas sind gleichgroß. Somit entstehen zwei volumengleiche Teilkörper, indem das große Prisma entlang des durch die Mittelpunkte der drei Seitenkanten aufgespannten Dreiecks zerlegt wird.
d)
Begründen, dass die --Ebene schneidet
Die -Koordinaten der beiden Endpunkte und besitzen unterschiedliche Vorzeichen, somit schneidet die Kante die --Ebene.
Koordinaten des Schnittpunktes bestimmen
Die eindeutige Gerade durch die Punkte und besitzt folgende mögliche Geradengleichung:
Ein allgemeiner Punkt in der --Ebene besitzt die Koordinaten Gleichsetzen mit der Geradengleichung von liefert folgendes lineares Gleichungssystem:
Lösen dieses Gleichungssystems mit dem CAS liefert und Der gesuchte Schittpunkt besitzt somit die Koordinaten
2
a)
Da die Reihenfolge, in der die Haushalte ausgewählt werden, keine Rolle spielt, ergeben sich verschiedene Möglichkeiten für das Ereignis und es folgt:
Die Wahrscheinlichkeit für einen Haushalt mit 2 oder weniger Personen beträgt Für das Ereignis folgt somit:
b)
Die Zufallsvariable die die Anzahl der Zweipersonenhaushalte angibt, ist binomialverteilt mit den Parametern und Mit dem CAS folgt:
Die Zufallsvariable die die Anzahl der Haushalte mit mehr als zwei Personen angibt, ist binomialverteilt mit den Parametern und Mit dem CAS ergibt sich:
c)
Die Zufallsvariable die die Anzahl der Haushalte mit vier oder mehr Personen angibt, ist binomialverteiltmit mit unbekanntem und Mit der allgemeinen Formel der Binomialgleichung folgt:
Es müssen somit mindestens Haushälte befragt werden, damit mit einer Wahrscheinlichkeit von mindestens mindestens zwei Haushalte mit vier oder mehr Personen darunter sind.
Mit Hilfe des nsolve-Befehls des CAS folgt:
d)
Wahrscheinlichkeit für Fehler erster Art berechnen
Die Zufallsvariable die die Anzahl der Haushalte mit drei oder mehr Personen angibt, ist binomialverteilt mit den Parametern und Mit dem CAS folgt für die Wahrscheinlichkeit des Fehlers erster Art:
Wahrscheinlichkeit für Fehler zweiter Art berechnen
Die Zufallsvariable die die Anzahl der Haushalte mit drei oder mehr Personen angibt, ist nun binomialverteilt mit den Parametern und Mit dem CAS folgt für die Wahrscheinlichkeit des Fehlers zweiter Art somit: