Teil C1

Gegeben ist eine Pyramide $ABCDS$ mit $A(2 \mid 0 \mid 0),$ $B(4\mid 2\mid 0),$ $C(2 \mid 4 \mid 0),$ $D(0 \mid 2 \mid 0),$ $S(2 \mid 2 \mid 4).$

Zeichne diese Pyramide in ein Koordinatensystem. Achte dabei auf verdeckte Körperkanten.
Beschreibe die besondere Lage der Pyramide im Koordinatensystem.

(4 BE)

Zeige, dass es sich um eine gerade quadratische Pyramide handelt.

(4 BE)

Berechne das Volumen der Pyramide.

(2 BE)

Berechne die Größe des Neigungswinkels einer Seitenfläche zur Grundfläche.

(2 BE)

Gegeben ist die Schar von Geraden $g_a$ mit $g_a : \overrightarrow{x} = \pmatrix{0\\0\\2}+r \cdot \pmatrix{1\\a\\0} \;\; (a,r \in \mathbb{R}).$

Bestimme die Werte von $a$ , für die die Gerade mit der Pyramide gemeinsame Punkte besitzt.

(4 BE)

Alle Eckpunkte der Pyramide liegen auf einer Kugel.
Berechne die Koordinaten des Mittelpunktes der Kugel.

(3 BE)

Es gibt Ebenen, die die Pyramiden in zwei volumengleiche Teile zerlegen.
Gib für zwei solche Ebenen je eine Gleichung an.

(2 BE)

Die Pyramide wird in die $xy$ -Ebene gekippt. Die umgekippte Pyramide wird mit $\(A$ bezeichnet. Dabei gilt $\(B$ und $\(S$ liegt in der $xy$ -Ebene.

Berechne die Koordinaten des Punktes $\(S$ .

(4 BE)

„Im Bundesland Thüringen hatten am 12.07.2021 genau 1 141 725 Personen eine Erstimpfung gegen das Coronavirus erhalten, davon waren sogar 870 050 Personen zweimal geimpft. Das entspricht $53,5 \,\%$ der Thüringerinnen und Thüringer mit Erstimpfung und $40,8\,\%$ mit Zweitimpfung.“

Aus: https:\\www.facebook.com (12.07.2021)

Am selben Tag werden auf einem Wochenmarkt in Thüringen Personen zufällig ausgewählt und zu ihrem Impfstatus befragt.
Zur Auswertung der Befragung soll das Modell der Binomialverteilung angewendet werden.

Gib zwei Gründe im Sachzusammenhang dafür an, dass man die Anzahl der zweimal geimpften Personen als binomialverteilt mit $p=0,408$ ansehen kann.
Gib einen auf den Sachverhalt bezogene Grenze dieses Modells an.

(3 BE)

Bestimme die Wahrscheinlichkeit folgender Ereignisse:

A: = „Von 100 befragten Personen sind 40 oder 41 zweimal geimpft.“

B: = „Von 100 befragten Personen ist mindestens die Hälfte zweimal geimpft.“

(4 BE)

Betrachtet wird das Ereignis C:

C: = „Von $n$ befragten Personen geben mindestens 80 an, zweimal geimpft zu sein.“

Bestimme die Mindestanzahl $n$ der befragten Personen so, dass $P(C) \gt 0,8$ gilt.

(2 BE)

Beschreibe in diesem Sachzusammenhang ein Ereignis D, dessen Wahrscheinlichkeit durch

Gleichung anzeigen

berechnet werden kann.

(2 BE)

Von 100 befragten Personen gaben 53 an, bereits zweimal geimpft zu sein.
Untersuche mit einer Sicherheitswahrscheinlichkeit von $95\,\%$ , ob dieses Ergebnis mit der Angabe „ $40,8\,\%$ der Thüringer haben eine Zweitimpfung erhalten.“, verträglich ist.

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

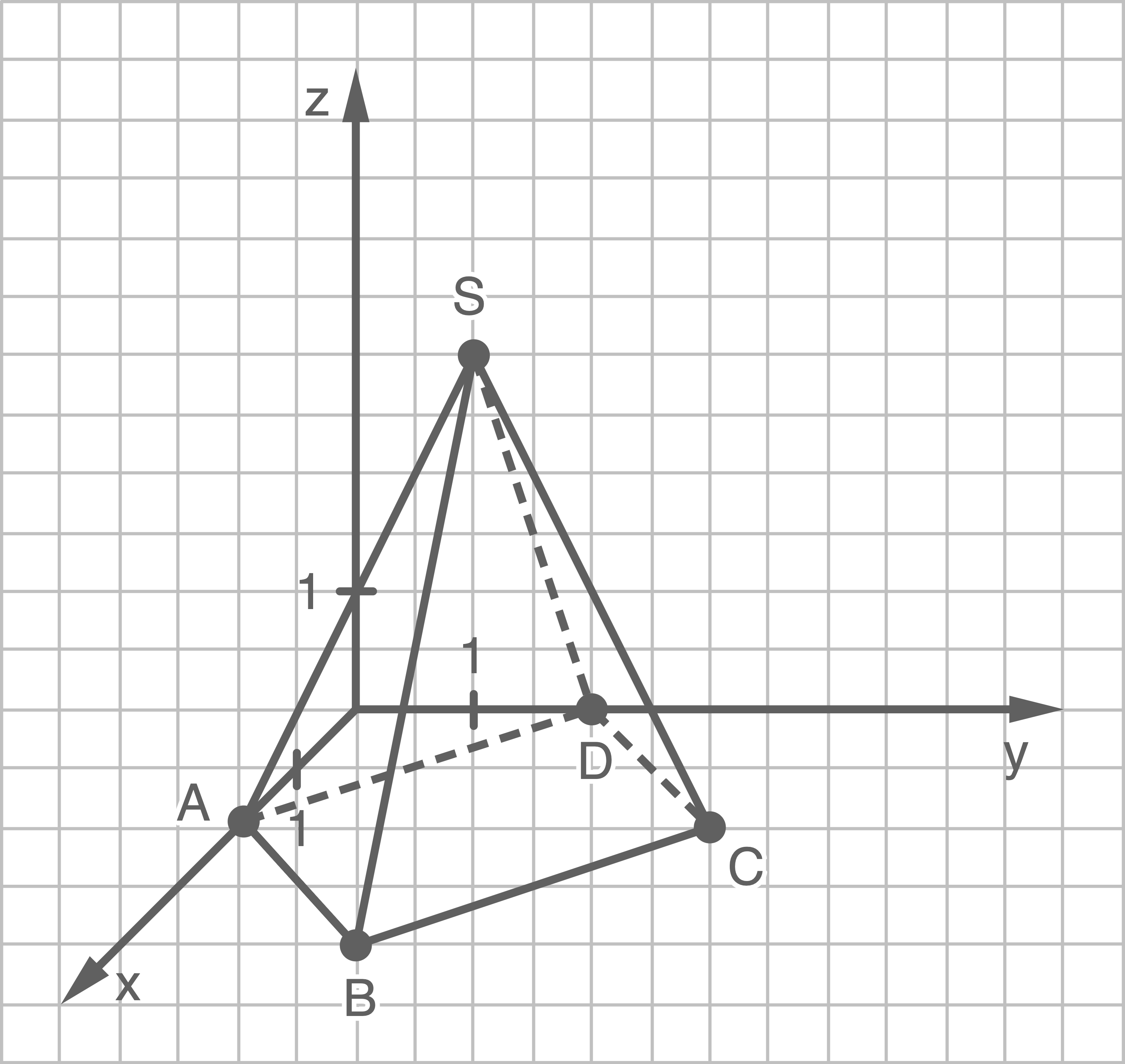
Die Grundfläche der Pyramide liegt in der $xy$ -Ebene.

Nachweis Quadrat

$\mid \overrightarrow{AB} \mid =2 \sqrt{2}$

$\mid \overrightarrow{BC} \mid =2 \sqrt{2}$

$\mid \overrightarrow{CD} \mid =2 \sqrt{2}$

$\mid \overrightarrow{DA} \mid =2 \sqrt{2}$

Somit ist gezeigt, dass alle Seiten gleich lang sind.

$\overrightarrow{AB} \circ \overrightarrow{BC}=0$ und $\overrightarrow{CD} \circ \overrightarrow{DA}=0.$

Alle Punkte der Grundfläche der Pyramide $ABCD$ liegen in der $xy$ -Ebene.

Der Mittelpunkt der Diagonalen $\overline{AC}$ hat die Koordinaten $M(2 \mid 2\mid 0).$ Der Mittelpunkt der Diagonalen $\overline{BD}$ entspricht ebenfalls $M.$ Aus den Koordinaten von $S$ kann abgelesen werden, dass die Pyramidenspitze über $M$ liegt.

Folglich handelt es sich um eine gerade quadratische Pyramide.

$V=\dfrac{1}{3}\cdot G\cdot h$ $=\dfrac{1}{3}\cdot (2\sqrt{2})^2 \cdot 4= \dfrac{32}{3} \;\text{[VE]}$

$\overrightarrow{AS}= \pmatrix{0\\2\\4}$

$\overrightarrow{BS}= \pmatrix{-2\\0\\4}$

$\overrightarrow{n_S}= \overrightarrow{AS} \times \overrightarrow{BS} = \pmatrix{8\\-8\\4}$

Ein Normalenvektor der $xy$ -Ebene ist $\overrightarrow{n_B}=\pmatrix{0\\0\\1}$

$\alpha = \cos^{-1}\left(\dfrac{\mid \overrightarrow{n_S} \cdot \overrightarrow{n_B} \mid }{\mid\overrightarrow{n_S} \mid \circ \mid\overrightarrow{n_B} \mid} \right)$ $=\dfrac{4}{\sqrt{8^2+(-8)^2+4^2}}$

$\alpha \approx 70,53 ^{\circ}$

Dem Stützvektor der Geradenschar ist zu entnehmen, dass die Gerade durch die $z$ -Achse im Punkt $(0 \mid 0 \mid 2)$ verläuft. Den größten Abstand haben $B$ und $C.$

Es wird also bestimmt, für welche Werte von $a$ die Geradenschar durch $B$ und $C$ verläuft.

Punktprobe mit $B$

Rechenweg anzeigen

$\pmatrix{4\\2\\-2} = r \cdot \pmatrix{1\\a\\0}$

Aus der ersten Zeile folgt $r=4,$ aus der zweiten folgt $2=r\cdot a= 4\cdot a$ und somit $a= \dfrac{1}{2}.$

Punktprobe mit $C$

Rechenweg anzeigen

$\pmatrix{2\\4\\-2} = r \cdot \pmatrix{1\\a\\0}$

Aus der ersten Zeile folgt $r=2,$ aus der zweiten folgt $2=r\cdot a= 2\cdot a$ und somit $a= 2.$

Für $\dfrac{1}{2} \leq a \leq 2$ besitzt die Gerade somit mit der Pyramide gemeinsame Punkte.

1. Schritt: Geradengleichung aufstellen

Zunächst wird eine Geradengleichung aufgestellt, auf der der Mittelpunkt des Kreises liegt.

$\overrightarrow{SM}= \overrightarrow{OM}- \overrightarrow{OS}$ $= \pmatrix{2\\2\\0}-\pmatrix{2\\2\\4} = \pmatrix{0\\0\\-4}$

$h: \overrightarrow{x} = \pmatrix{2\\2\\0} +s \cdot \pmatrix{0\\0\\-4}$

Für den Mittelpunkt $M_K$ des Kreises folgt $\overrightarrow{OM_K}=\pmatrix{2\\2\\-4\cdot s}.$

2. Schritt: Koordinaten des Mittelpunktes bestimmen

Es gilt: $d(\overrightarrow{M_KS}))$ $= \left| \pmatrix{2-2\\2-2\\4-(-4s)} \right|$ $=4+4\cdot s$

$d(\overrightarrow{M_KA}))$ $= \left| \pmatrix{2-2\\0-2\\0-(-4s)} \right|$ $=\sqrt{(-2)^2+4^2s^2}$

Gleichsetzen ergibt:

Rechenweg anzeigen

$s= -0,375$

Einsetzen in $\overrightarrow{OM_K}$ ergibt die Koordinaten:

$M_K(2 \mid 2 \mid 1,5)$

$\varepsilon_1: x=2$

$\varepsilon_2: y=2$

Mittelpunkt der Strecke $\overline{BC}$ bestimmen

$\overrightarrow{BC}= \pmatrix{-2\\2\\0}$

$\overrightarrow{OM_{BC}}=\overrightarrow{OB} +\dfrac{1}{2}\cdot \overrightarrow{BC}$ $= \pmatrix{3\\3\\0}$

Abstand zwischen $OM_{BC}$ und $S$ bestimmen

$d(\overrightarrow{M_{BC}S})= \left| \pmatrix{2-3\\2-3\\4-0} \right|$ $= \sqrt{(-1)^2+(-1)^2+4^2}$ $=3\sqrt{2}$

Orthogonaler Vektor zu $\overrightarrow{BC}$

Ein zu $\overrightarrow{BC}$ orthogonaler Vektor ist beispielsweise $\overrightarrow{v}=\pmatrix{2\\2\\0}$

Normieren von $\overrightarrow{v}$ liefert $\hat{v} =\dfrac{1}{\sqrt{2^2+2^2}}\cdot \pmatrix{2\\2\\0}$

Koordinaten des Punktes $\(S$ bestimmen

$\(\overrightarrow{OS$ $=\pmatrix{6\\6\\0}$

$\(S$

Gründe angeben

zweimal geimpft ja/nein
unabhängige Befragung der Personen

Grenze des Modells

Eine ungleiche regionale Verteilung beim Impfstatus stellt eine Grenze dar.

$P ( A )= B _{100 ; 0,408}(40 \leq X \leq 41)$ $\approx 0,1610$

$P ( B )= B _{100: 0.408}( X \geq 50) \approx 0,0392$

Systematisches Ausprobieren mit dem CAS:

$B _{209 ; 0,408}(X \geq 80) \approx 0,7913 \lt 0,8$

$B_{210 ; 0,408}(X \geq 80) \approx 0,8069\gt 0,8$

Somit folgt $n=210.$

Von 10 befragten Personen sind mindestens 5 und maximal 7 zweimal geimpft.

Prognoseintervall für $n =100 ; p =0,408$

$B _{100 ; 0,408}(31 \leq X \leq 50) \approx 0,9582$

$B _{100 ; 0,408}(31 \leq X \leq 51) \approx 0,9678$

$53 \notin[31 ; 50]$ , also nicht verträglich

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?