Teil B
Gegeben sind eine Funktion  durch
durch  und für jede reelle Zahl
und für jede reelle Zahl 
 eine Funktion
eine Funktion  durch
durch  jeweils mit
jeweils mit 
 für
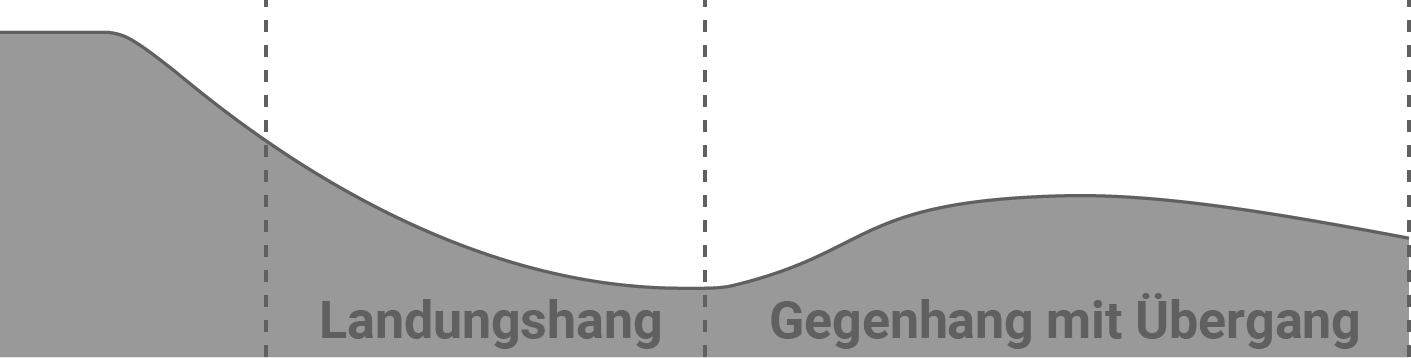
für  als Landungshang nach einem Sprung und der Funktion
als Landungshang nach einem Sprung und der Funktion  für
für  als Gegenhang mit dem anschließenden Übergang in eine Steilkurve modelliert. (
als Gegenhang mit dem anschließenden Übergang in eine Steilkurve modelliert. ( und
und  in Metern)
in Metern)
a)
Untersuche die Graphen von  auf lokale Extrempunkte.
auf lokale Extrempunkte.
Zeige, dass alle Extrempunkte der Graphen von auf dem Graphen von
auf dem Graphen von  liegen.
liegen.
Zeige, dass alle Extrempunkte der Graphen von
(7 BE)
b)
Die Gerade  schneidet die Graphen von
schneidet die Graphen von  .
.
Bestimme die Anzahl der Schnittpunkte dieser Geraden mit den Graphen von in Abhängigkeit von
in Abhängigkeit von  .
.
Bestimme die Anzahl der Schnittpunkte dieser Geraden mit den Graphen von
(4 BE)
c)
Die Graphen von  und der Graph von
und der Graph von  begrenzen jeweils eine Fläche mit dem Flächeninhalt
begrenzen jeweils eine Fläche mit dem Flächeninhalt  vollständig.
vollständig.
Ermittle in Abhängigkeit von
in Abhängigkeit von  .
.
Bestimme das Verhältnis der Flächeninhalte bei Verdopplung von .
.
Ermittle
Bestimme das Verhältnis der Flächeninhalte bei Verdopplung von
(4 BE)
d)
Für  bilden der Koordinatenursprung sowie die Punkte
bilden der Koordinatenursprung sowie die Punkte  und
und  mit
mit  ein Dreieck.
ein Dreieck.
Berechne so, dass der Flächeninhalt dieses Dreiecks maximal ist.
so, dass der Flächeninhalt dieses Dreiecks maximal ist.
Gib diesen Flächeninhalt an.
Für den Bau einer Skicrossstrecke wird ein Teil der Profillinie durch die Graphen der Funktion Berechne
Gib diesen Flächeninhalt an.
(5 BE)

Skizze nicht maßstäblich
e)
Begründe, dass der Landungshang knickfrei in den Gegenhang übergeht.
(2 BE)
f)
Berechne das größte Gefälle im Landungshang und die größte Steigung im Gegenhang in Prozent.
(6 BE)
g)
Am Landungshang soll der Landebereich Neigungswinkel von  bis
bis  gegenüber der Horizontalen annehmen.
gegenüber der Horizontalen annehmen.
Bestimme das Intervall für so, dass dieser Landebereich beschrieben wird.
so, dass dieser Landebereich beschrieben wird.
Bestimme das Intervall für
(4 BE)
h)
Zur Ausleuchtung der Strecke wird an der Stelle, die im Modell  entspricht, ein Mast mit einem Scheinwerfer aufgestellt. Der Scheinwerfer wird zunächst in einer Höhe von zwei Meter über dem Gegenhang montiert und als punktförmige Lichtquelle betrachtet.
entspricht, ein Mast mit einem Scheinwerfer aufgestellt. Der Scheinwerfer wird zunächst in einer Höhe von zwei Meter über dem Gegenhang montiert und als punktförmige Lichtquelle betrachtet.
Weise nach, dass der Scheinwerfer in dieser Höhe den tiefsten Punkt des betrachteten Teils der Profillinie nicht ausleuchten kann.
Berechne die Länge der Strecke, um die der Scheinwerfer mindestens angehoben werden muss, damit ein Lichtstrahl den tiefsten Punkt trifft.
Weise nach, dass der Scheinwerfer in dieser Höhe den tiefsten Punkt des betrachteten Teils der Profillinie nicht ausleuchten kann.
Berechne die Länge der Strecke, um die der Scheinwerfer mindestens angehoben werden muss, damit ein Lichtstrahl den tiefsten Punkt trifft.
(8 BE)
a)
Graphen auf lokale Extrempunkte untersuchen
Mit Hilfe des CAS folgt für die Ableitungen von 


 1. Schritt: Notwendige Bedingung für Extremstellen anwenden
1. Schritt: Notwendige Bedingung für Extremstellen anwenden
 Mit dem solve-Befehl des CAS folgt:
Mit dem solve-Befehl des CAS folgt:
![\(\begin{array}[t]{rll}
x_1&=& 0 \\[5pt]
x_2&=& 2t \\[5pt]
\end{array}\)](https://mathjax.schullv.de/3b7f6eb9f0f667b341b9a0fa42b936352c9e97a1283a2c3e757f4988f9c2149e?color=5a5a5a) 2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
![\(\begin{array}[t]{rll}
f_t](https://mathjax.schullv.de/530fb63130e4366794da603631bc8bb28e3582ec749b758767cecae74a442cec?color=5a5a5a)
![\(\begin{array}[t]{rll}
f_t](https://mathjax.schullv.de/861bb348f3ead7ba07d8f659aa9bc0f6149469ebac5b19896c8d4ea278729b7a?color=5a5a5a) Einsetzen von
Einsetzen von  und
und  in
in  liefert weiter:
liefert weiter:
![\(\begin{array}[t]{rll}
f_t(0)&=& 0 \\[5pt]
f_t(2t)&=& 2t^2\cdot \mathrm e^{-2} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/27c800df337c658b365c5b5100021efeade8c844489dc9bd645917d95703e840?color=5a5a5a) Die Graphen von
Die Graphen von  besitzen somit den Tiefpunkt
besitzen somit den Tiefpunkt  und den Hochpunkt
und den Hochpunkt  Lage zeigen
Einsetzen der Extremstellen in den Funktionsterm von
Lage zeigen
Einsetzen der Extremstellen in den Funktionsterm von  liefert:
liefert:





 Somit liegen alle Extrempunkte der Graphen von
Somit liegen alle Extrempunkte der Graphen von  auf dem Graphen von
auf dem Graphen von 
b)
Der Tiefpunkt  der Schar liegt für jeden Wert von
der Schar liegt für jeden Wert von  unterhalb der Geraden
unterhalb der Geraden  Die Gerade verläuft parallel zur
Die Gerade verläuft parallel zur  -Achse, die Anzahl der Schnittpunkte hängt also davon ab, ob der Hochpunkt
-Achse, die Anzahl der Schnittpunkte hängt also davon ab, ob der Hochpunkt  oberhalb, unterhalb oder auf der Geraden liegt. Gleichsetzen der
oberhalb, unterhalb oder auf der Geraden liegt. Gleichsetzen der  -Koordinate von
-Koordinate von  mit
mit  liefert:
liefert:
![\(\begin{array}[t]{rll}
2 t^2 \cdot \mathrm e^{-2} &=& 2 &\quad \scriptsize \mid\; :2 \\[5pt]
t^2\cdot \mathrm e^{-2} &=& 1 &\quad \scriptsize \mid\; \cdot\mathrm e^{2} \\[5pt]
t^2 &=& \mathrm e^{2} &\quad \scriptsize \mid\; \sqrt{\;} \\[5pt]
t &=& \pm\mathrm e
\end{array}\)](https://mathjax.schullv.de/138ec403d9088e972d100b0d445b28599227ed474946f302727852b1b8313776?color=5a5a5a) Da
Da  gilt, kommt nur
gilt, kommt nur  infrage. Da die
infrage. Da die  -Funktion stets positiv ist, wird für größeres
-Funktion stets positiv ist, wird für größeres  auch
auch  größer bzw. für kleineres
größer bzw. für kleineres  kleiner. Somit folgt:
kleiner. Somit folgt:
- ein Schnittpunkt für
- zwei Schnittpunkte für
- drei Schnittpunkte für
c)
d)
Wert von  berechnen
Da die
berechnen
Da die  -Koordinaten von
-Koordinaten von  und
und  identisch sind, besitzt das Dreieck
identisch sind, besitzt das Dreieck  im Punkt
im Punkt  einen rechten Winkel. Der Flächeninhalt des Dreiecks ergibt sich somit in Abhängigkeit von
einen rechten Winkel. Der Flächeninhalt des Dreiecks ergibt sich somit in Abhängigkeit von  wie folgt:
wie folgt:
![\(\begin{array}[t]{rll}
A(u) &=& \dfrac{1}{2}\cdot \vert\overline{PQ}\vert \cdot \vert\overline{OP}\vert \\[5pt]
&=& \dfrac{1}{2}\cdot f_2(u) \cdot u \\[5pt]
&=& \dfrac{1}{2}\cdot \dfrac{u^2}{2}\cdot \mathrm e^{-\frac{u}{2}}\cdot u \\[5pt]
&=& \dfrac{1}{4}\cdot u^3\cdot \mathrm e^{-\frac{u}{2}} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/b5bf33f9b6354d8770c3d6117fc231ad05625094d8d18259552a90914215b493?color=5a5a5a) Ableiten nach
Ableiten nach  im CAS liefert für die ersten beiden Ableitungsfunktionen von
im CAS liefert für die ersten beiden Ableitungsfunktionen von 




 1. Schritt: Notwendiges Kriterium für Extremstellen anwenden
Auflösen von
1. Schritt: Notwendiges Kriterium für Extremstellen anwenden
Auflösen von  im CAS liefert:
im CAS liefert:
![\(\begin{array}[t]{rll}
u_1&=&0 \\[5pt]
u_2&=&6
\end{array}\)](https://mathjax.schullv.de/15cc19caf2e2b24e9e8f540e4234de7d4f1fe693b6dc18a030da52c5928288e3?color=5a5a5a) Da
Da  in der Aufgabenstellung vorgegeben ist, kommt als mögliche Extremstelle nur
in der Aufgabenstellung vorgegeben ist, kommt als mögliche Extremstelle nur  infrage.
2. Schritt: Hinreichendes Kriterium für Extremstellen überprüfen
Da
infrage.
2. Schritt: Hinreichendes Kriterium für Extremstellen überprüfen
Da  besitzt die Funktion
besitzt die Funktion  an der Stelle
an der Stelle  also einen Hochpunkt.
also einen Hochpunkt.
Der Flächeninhalt des Dreiecks ist somit für maximal.
Flächeninhalt angeben
maximal.
Flächeninhalt angeben
![\(\begin{array}[t]{rll}
A(6) &=& \dfrac{6^3}{4}\cdot \mathrm e^{-\frac{6}{2}} \\[5pt]
&=& 54\cdot \mathrm e^{-3}\;[\text{FE}]
\end{array}\)](https://mathjax.schullv.de/2d5bd02ff14262d9319a013043ebfb19e91c8261a6d8b382f7ccbc217c22d34a?color=5a5a5a) Der maximale Flächeninhalt des Dreiecks beträgt damit
Der maximale Flächeninhalt des Dreiecks beträgt damit  Flächeneinheiten.
Flächeneinheiten.
Der Flächeninhalt des Dreiecks ist somit für
e)
Nach Aufgabenteil a) liegt der Tiefpunkt  des Graphen
des Graphen  an der Übergangsstelle
an der Übergangsstelle  auch auf dem Graph von
auch auf dem Graph von  das heißt beide Funktionen nehmen den gleichen Funktionswert an. Da
das heißt beide Funktionen nehmen den gleichen Funktionswert an. Da  ein Tiefpunkt des Graphen von
ein Tiefpunkt des Graphen von  ist, gilt
ist, gilt  Für die Steigung des Graphen von
Für die Steigung des Graphen von  folgt:
folgt:
![\(\begin{array}[t]{rll}
g(x)&=& \dfrac{1}{2\mathrm e^2}\cdot x^2 \\[10pt]
g](https://mathjax.schullv.de/183febda7287ecc706938616fe259e23b68d251911b7fc72cdda0878cf7c5e3d?color=5a5a5a) Da sowohl der Funktionswert als auch die Steigung der beiden Funktionen an der Übergangsstelle übereinstimmen, ist der Übergang zwischen Landungshang und Gegenhang somit knickfrei.
Da sowohl der Funktionswert als auch die Steigung der beiden Funktionen an der Übergangsstelle übereinstimmen, ist der Übergang zwischen Landungshang und Gegenhang somit knickfrei.
f)
Größtes Gefälle im Landungshang berechnen
Die Steigung des Landungshangs wird durch  beschrieben. Da
beschrieben. Da  handelt es sich bei dem Graphen von
handelt es sich bei dem Graphen von  um eine Gerade mit positiver Steigung. Der kleinste Funktionswert von
um eine Gerade mit positiver Steigung. Der kleinste Funktionswert von  das heißt die geringste Steigung, ist somit gegeben durch den Funktionswert am Beginn des betrachteten Intervalls bei
das heißt die geringste Steigung, ist somit gegeben durch den Funktionswert am Beginn des betrachteten Intervalls bei 



 Das größte Gefälle im Landungshang beträgt somit ca.
Das größte Gefälle im Landungshang beträgt somit ca.  Größte Steigung im Gegenhang berechnen
Die Steigung des Gegenhangs wird durch
Größte Steigung im Gegenhang berechnen
Die Steigung des Gegenhangs wird durch  beschrieben. Ableiten im CAS liefert weiter:
beschrieben. Ableiten im CAS liefert weiter:

 1. Schritt: Notwendiges Kriterium für Extremstellen anwenden
Auflösen von
1. Schritt: Notwendiges Kriterium für Extremstellen anwenden
Auflösen von  mit dem solve-Befehl des CAS liefert:
mit dem solve-Befehl des CAS liefert:
![\(\begin{array}[t]{rll}
x_1&=&4- \sqrt{8} \\[5pt]
x_2&=&4+ \sqrt{8}
\end{array}\)](https://mathjax.schullv.de/1185867396730a7d0006bbb7171991378bff3251df9f108633fcfacfae9d5b92?color=5a5a5a) 2. Schritt: Hinreichendes Kriterium für Extremstellen überprüfen
An der Stelle
2. Schritt: Hinreichendes Kriterium für Extremstellen überprüfen
An der Stelle  besitzt
besitzt  somit einen Hochpunkt und an der Stelle
somit einen Hochpunkt und an der Stelle  einen Tiefpunkt.
3. Schritt: Intervalränder untersuchen
einen Tiefpunkt.
3. Schritt: Intervalränder untersuchen
![\(\begin{array}[t]{rll}
f_2](https://mathjax.schullv.de/516600d44f969b950e63ad06265f02234dd55797acf65756299ff9ef5c9b78bd?color=5a5a5a) Der CAS liefert zudem
Der CAS liefert zudem  somit beträgt die größte Steigung im Gegenhang ca.
somit beträgt die größte Steigung im Gegenhang ca. 
g)
Da der Landungshang fällt, entsprechen die gesuchten Neigungswinkel  und
und  den Steigungswinkeln
den Steigungswinkeln  und
und  des Graphen von
des Graphen von 
Mit Hilfe der Gleichung für den Steigungswinkel liefert das die folgende Ungleichung: Auflösen nach
Auflösen nach  mit dem solve-Befehl des CAS liefert:
mit dem solve-Befehl des CAS liefert:
 Da der Landungshang für
Da der Landungshang für  definiert ist, wird der gesuchte Landebereich somit durch
definiert ist, wird der gesuchte Landebereich somit durch  beschrieben.
beschrieben.
Mit Hilfe der Gleichung für den Steigungswinkel liefert das die folgende Ungleichung:
h)
Nachweisen, dass der Scheinwerfer den Punkt nicht ausleuchten kann
Der Scheinwerfer befindet sich zunächst im Punkt  1. Schritt: Tiefsten Punkt der Profillinie bestimmen
Der Punkt
1. Schritt: Tiefsten Punkt der Profillinie bestimmen
Der Punkt  ist der einzige lokale Tiefpunkt des Graphen von
ist der einzige lokale Tiefpunkt des Graphen von  Da es sich bei diesem Graphen um eine nach oben geöffnete Parabel handelt, ist der Tiefpunkt der tiefste Punkt des Graphen.
Da es sich bei diesem Graphen um eine nach oben geöffnete Parabel handelt, ist der Tiefpunkt der tiefste Punkt des Graphen.
 ist nach ebenfalls der einzige lokale Tiefpunkt des Graphen von
ist nach ebenfalls der einzige lokale Tiefpunkt des Graphen von  Die einzige Stelle auf der Profillinie des Gegenhangs, in der die Profillinie tiefer sein könnte, ist der Intervallrand
Die einzige Stelle auf der Profillinie des Gegenhangs, in der die Profillinie tiefer sein könnte, ist der Intervallrand  Da sich der Scheinwerfer aber genau an dieser Stelle unmittelbar über dem Gegenhang befindet, kann diese Stelle definitiv ausgeleuchtet werden.
Da sich der Scheinwerfer aber genau an dieser Stelle unmittelbar über dem Gegenhang befindet, kann diese Stelle definitiv ausgeleuchtet werden.
Der tiefste Punkt der Profillinie ist also der Tiefpunkt 2. Schritt: Geradengleichung aufstellen
Das Licht vom Scheinwerfer zum tiefsten Punkt verläuft entlang der Geraden durch die Punkte
2. Schritt: Geradengleichung aufstellen
Das Licht vom Scheinwerfer zum tiefsten Punkt verläuft entlang der Geraden durch die Punkte  und
und  Für die Steigung der Gerade folgt somit:
Für die Steigung der Gerade folgt somit:
![\(\begin{array}[t]{rll}
m &=& \dfrac{y_S-y_T }{ x_S-x_T } \\[5pt]
&=& \dfrac{f_2(8)+2 - 0}{8-0} \\[5pt]
&=& \dfrac{\frac{8^2}{2}\cdot \mathrm e^{-\frac{8}{2}} +2 }{8} \\[5pt]
&=& 4\cdot \mathrm e^{-4} + \dfrac{1}{4}
\end{array}\)](https://mathjax.schullv.de/af1fee757ae6b6d957683abb42b3764a2cd2469409e1de708d9369be34a7cb09?color=5a5a5a) Da die Gerade durch den Punkt
Da die Gerade durch den Punkt  verläuft, ergibt sich insgesamt:
verläuft, ergibt sich insgesamt:
 3. Schritt: Schnittpunkte bestimmen
Gleichsetzen der Gerade
3. Schritt: Schnittpunkte bestimmen
Gleichsetzen der Gerade  und der Funktion
und der Funktion  die den Gegenhang beschreibt, liefert mit dem solve-Befehl des CAS:
die den Gegenhang beschreibt, liefert mit dem solve-Befehl des CAS:
![\(\begin{array}[t]{rll}
x_1 &=& 0 \\[5pt]
x_2 &\approx& 1,15 \\[5pt]
x_3 &\approx& 3,20
\end{array}\)](https://mathjax.schullv.de/ef88fe4e19e5bb3dfc0ff8b6a8144511dfe85bcdb919f5a4b7788521fb8bda8c?color=5a5a5a) Die Gerade entlang derer die Lichtstrahlen einfallen schneiden den Gegenhang vor dem tiefsten Punkt, somit kann der Scheinwerfer von dieser Position aus nicht den tiefsten Punkt der Profillinie ausleuchten.
Länge der Strecke berechnen
Der angehobene Scheinwerfer hat die neuen Koordinaten
Die Gerade entlang derer die Lichtstrahlen einfallen schneiden den Gegenhang vor dem tiefsten Punkt, somit kann der Scheinwerfer von dieser Position aus nicht den tiefsten Punkt der Profillinie ausleuchten.
Länge der Strecke berechnen
Der angehobene Scheinwerfer hat die neuen Koordinaten  Er kann den tiefsten Punkt ausleuchten, sobald die Gerade, entlang derer die Lichtstrahlen einfallen, die Profillinie lediglich berührt, wenn sie also eine Tangente an den Graphen von
Er kann den tiefsten Punkt ausleuchten, sobald die Gerade, entlang derer die Lichtstrahlen einfallen, die Profillinie lediglich berührt, wenn sie also eine Tangente an den Graphen von  in einem Punkt
in einem Punkt  mit
mit  ist.
1. Schritt: Tangente bestimmen
Die Steigung der Tangente an den Graphen von
ist.
1. Schritt: Tangente bestimmen
Die Steigung der Tangente an den Graphen von  im Punkt
im Punkt  ist
ist  Da die Tangente den Punkt
Da die Tangente den Punkt  treffen soll, hat ihre Gleichung folgende Form:
treffen soll, hat ihre Gleichung folgende Form:
 Damit es sich um eine Tangente handelt, muss auch der Punkt
Damit es sich um eine Tangente handelt, muss auch der Punkt  auf
auf  liegen. Auflösen von
liegen. Auflösen von  nach
nach  mit Hilfe des solve-Befehls des CAS liefert:
mit Hilfe des solve-Befehls des CAS liefert:
 Die Steigung der Tangente ist somit gegeben durch:
Die Steigung der Tangente ist somit gegeben durch:
![\(\begin{array}[t]{rll}
f_2](https://mathjax.schullv.de/f515af91b594f334ced4a8fa67d1c637b43b9ee636a01d9324ab14cd43f3227e?color=5a5a5a) Insgesamt ergibt sich alo für die Tangente, die den Einfallsweg des Lichts beschreibt, folgende Gleichung:
Insgesamt ergibt sich alo für die Tangente, die den Einfallsweg des Lichts beschreibt, folgende Gleichung:
 2. Schritt: Koordinaten des Scheinwerfers berechnen
Einsetzen von
2. Schritt: Koordinaten des Scheinwerfers berechnen
Einsetzen von  in
in  liefert für die neue Höhe des Schneinwerfers:
liefert für die neue Höhe des Schneinwerfers:
 Der Scheinwerfer muss nun also in einer Höhe von mindestens
Der Scheinwerfer muss nun also in einer Höhe von mindestens  hängen. Die vorherige Höhe ist gegeben durch:
hängen. Die vorherige Höhe ist gegeben durch:
![\(\begin{array}[t]{rll}
f_2(8) +2 &=& \dfrac{8^2}{2}\cdot\mathrm e^{-\frac{8}{2}} +2 \\[5pt]
&=& 32\cdot\mathrm e^{-4} +2
\end{array}\)](https://mathjax.schullv.de/dbb2328900cf7885bab8634b8dbc6c3a37dd00b9890d1b6f6e671c3aa0ef57b3?color=5a5a5a) Die Höhendifferenz beträgt:
Die Höhendifferenz beträgt:

![\( \approx 0,36\;[\text{m}]\)](https://mathjax.schullv.de/d200640bc8f998f2e19863a981f10cc90583eb779fd80e31ccaedee205f0415c?color=5a5a5a) Der Scheinwerfer muss also mindestens um ca.
Der Scheinwerfer muss also mindestens um ca.  angehoben werden, damit er den tiefsten Punkt der Profillinie ausleuchtet.
angehoben werden, damit er den tiefsten Punkt der Profillinie ausleuchtet.
Der tiefste Punkt der Profillinie ist also der Tiefpunkt