Teil C1
1
Bei einer Fahrt in den Thüringer Wald entdeckte Paul die abgebildeten Häuschen. Beide Dächer sind pyramidenförmig, werden von unterschiedlich langen Stützpfeilern getragen und sind dadurch gegenüber dem Boden gekippt.
Angeregt davon möchte Paul für den Schulhof seiner Schule einen Lesepavillon konzipieren.
Angeregt davon möchte Paul für den Schulhof seiner Schule einen Lesepavillon konzipieren.
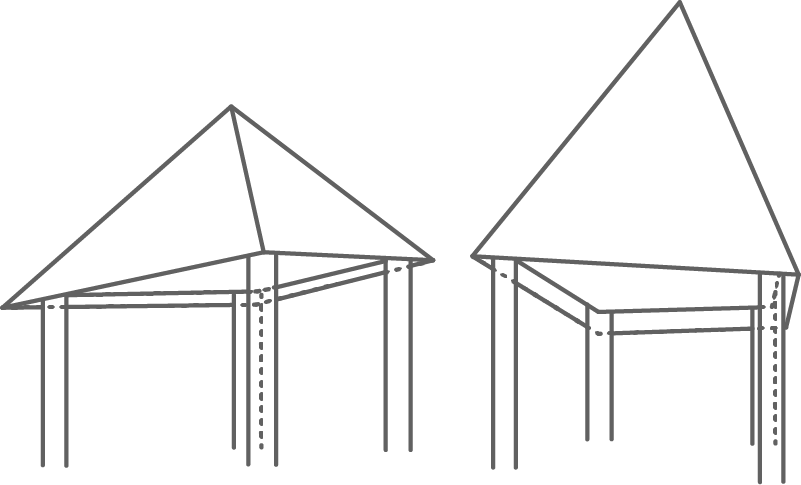
a)
Bestimme eine Koordinatengleichung der Grundflächenebene der Pyramide und ermittle deren Neigungswinkel gegenüber der  -Ebene.
-Ebene.
(5 BE)
b)
Ermittle die Koordinaten des Punktes  und der Spitze
und der Spitze  der Pyramide auf eine Dezimalstelle genau.
der Pyramide auf eine Dezimalstelle genau.
 Kontrollergebnis:
Kontrollergebnis: ![\(S(1,0\mid 2,0\mid 6,4) \big]\)](https://mathjax.schullv.de/ac9a968f02d3530196217583c7a20147bfcf186252d8d5468198373642709e79?color=5a5a5a)
(6 BE)
c)
Stelle die Pyramide in einem Koordinatensystem graphisch dar.
(2 BE)
d)
Berechne den Flächeninhalt einer dreieckigen Dachfläche.
(3 BE)
e)
Zwischen zwei diagonal gegenüberliegenden Stützpfeilern soll eine Sitzbank aufgestellt werden.
Berechne die maximale Länge einer solchen Sitzbank.
Auf der gesamten Dachfläche befinden sich einige Glasziegel, um einen guten Lichteinfall bei Tag zu gewährleisten. Zu einem bestimmten Zeitpunkt verlaufen Sonnenstrahlen in Richtung des Vektors Berechne die maximale Länge einer solchen Sitzbank.
(2 BE)
f)
Der Punkt, in dem ein Sonnenstrahl auf einen Glasziegel trifft, wird durch  modelliert. Untersuche, ob das Licht innerhalb der Bodenfläche des Pavillons auf den Boden trifft, wenn die Lichtbrechung unberücksichtigt bleibt.
modelliert. Untersuche, ob das Licht innerhalb der Bodenfläche des Pavillons auf den Boden trifft, wenn die Lichtbrechung unberücksichtigt bleibt.
(4 BE)
g)
Berechne den Einfallswinkel, unter dem die Sonnenstrahlen zu diesem Zeitpunkt auf die Dachfläche fallen, die im Modell der Fläche  entspricht.
entspricht.
(3 BE)
2
In der Broschüre „Mehr Nachhaltigkeit im Alltag“ hat das Bundesministerium für Ernährung und Landwirtschaft im Februar 2022 folgende Daten veröffentlicht:
 der Verbraucher legen Wert darauf, dass ihre Lebensmittel aus der Region stammen,
der Verbraucher legen Wert darauf, dass ihre Lebensmittel aus der Region stammen,  achten beim Einkauf auf das Bio-Siegel.
achten beim Einkauf auf das Bio-Siegel.
https://www.bmel.de (14.11.2022) Das Kaufverhalten von Kunden eines Supermarktes soll untersucht werden.
Dazu werden das Modell der Binomialverteilung und die relativen Häufigkeiten aus der Veröffentlichung als Wahrscheinlichkeiten verwendet.
https://www.bmel.de (14.11.2022) Das Kaufverhalten von Kunden eines Supermarktes soll untersucht werden.
Dazu werden das Modell der Binomialverteilung und die relativen Häufigkeiten aus der Veröffentlichung als Wahrscheinlichkeiten verwendet.

a)
Berechne die Wahrscheinlichkeit folgender Ereignisse:



„Von 35 Kunden legen genau 29 Wert auf regionale Produkte.“
„Von 60 Kunden achtet mindestens die Hälfte auf Produkte mit Bio-Siegel.“
„Von 5 Kunden, die hintereinander den Supermarkt betreten, achten nur die letzten beiden auf Produkte mit Bio-Siegel.“
(6 BE)
b)
Die Supermarktleitung möchte die Produktpalette an die Bedürfnisse der Kunden anpassen. Um zu überprüfen, ob der angegebene Anteil aus der Broschüre auch auf ihre Kunden zutrifft, sollen 200 Kunden zu ihrer Einstellung gegenüber regionalen Lebensmitteln befragt werden. Die Sicherheitswahrscheinlichkeit der Überprüfung soll  betragen.
betragen.
Bestimme die Mindestanzahl der Kunden, die bei dieser Befragung angeben, dass ihnen regionale Produkte wichtig sind, sodass der angegebene Anteil nicht angezweifelt werden muss.
Bestimme die Mindestanzahl der Kunden, die bei dieser Befragung angeben, dass ihnen regionale Produkte wichtig sind, sodass der angegebene Anteil nicht angezweifelt werden muss.
(3 BE)
c)
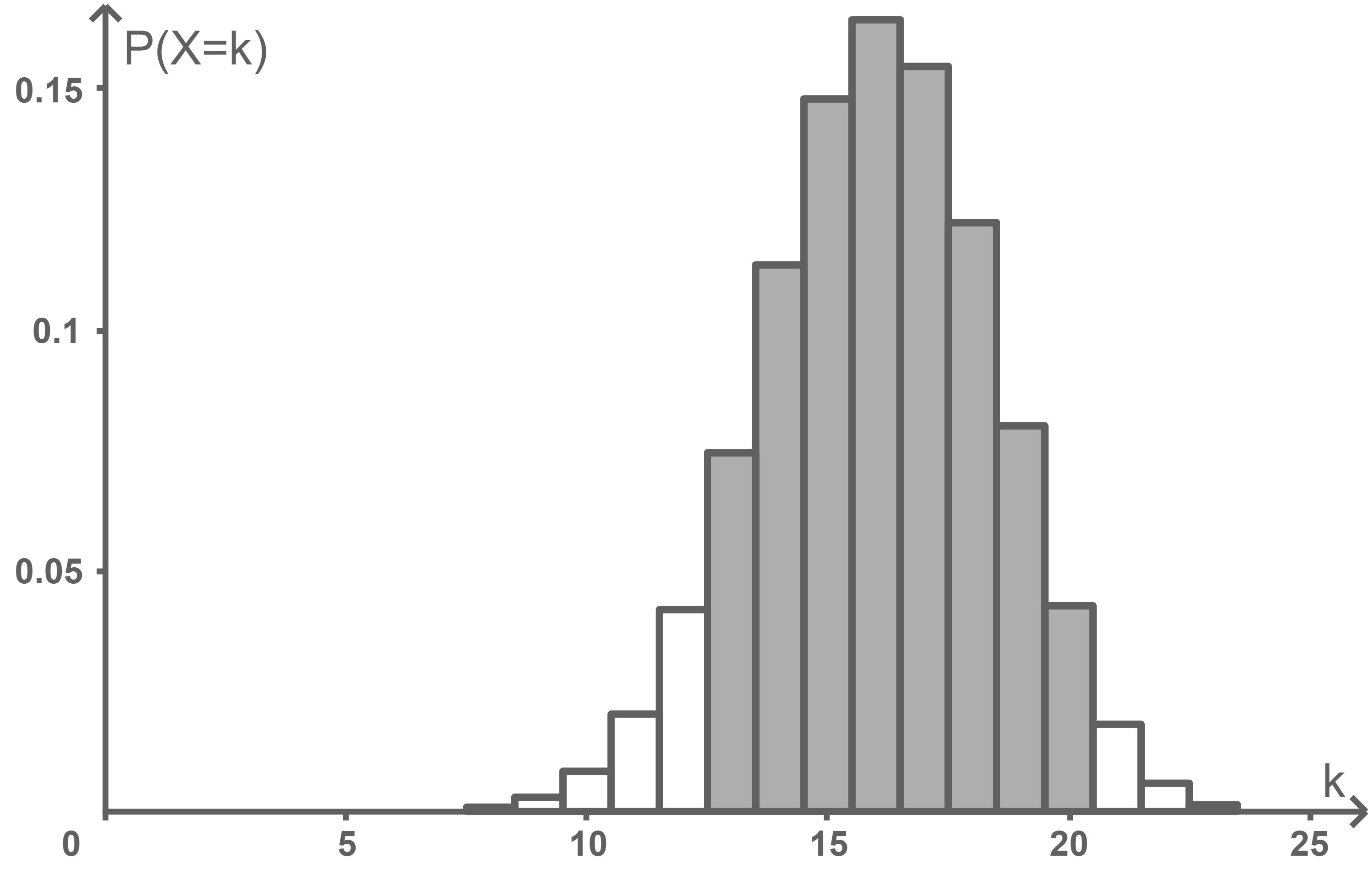
In der graphischen Darstellung sind die Wahrscheinlichkeitsverteilung einer binomialverteilten Zufallsgröße  mit
mit  sowie die Wahrscheinlichkeit des Ereignisses
sowie die Wahrscheinlichkeit des Ereignisses  als grau markierte Fläche gegeben.
als grau markierte Fläche gegeben.
Beschreibe das Ereignis bezogen auf den Sachzusammenhang.
bezogen auf den Sachzusammenhang.
Gib unter Verwendung des Summenzeichens einen Term an, mit dessen Hilfe die Wahrscheinlichkeit des Ereignisses berechnet werden kann.
berechnet werden kann.
Beschreibe das Ereignis
Gib unter Verwendung des Summenzeichens einen Term an, mit dessen Hilfe die Wahrscheinlichkeit des Ereignisses
(4 BE)
d)
Zur Ermittlung des Anteils der Verbraucher, die Wert auf regionale Produkte legen und ebenfalls auf das Bio-Siegel achten, wird folgender Ansatz vorgeschlagen:
 Beurteile diesen Ansatz.
Beurteile diesen Ansatz.
(2 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
a)
1. Schritt: Normalenvektor  berechnen
Die Ebene wird von den Vektoren
berechnen
Die Ebene wird von den Vektoren  und
und  aufgespannt. Für einen Normalenvektor
aufgespannt. Für einen Normalenvektor  folgt:
2. Schritt: Ebenengleichung aufstellen
folgt:
2. Schritt: Ebenengleichung aufstellen
 Einsetzen der Koordinaten von
Einsetzen der Koordinaten von  liefert:
liefert:
![\(\begin{array}[t]{rll}
-3+0+6\cdot4&=& d\\[5pt]
21&=& d
\end{array}\)](https://mathjax.schullv.de/5a250a14ab8e13ad9e170828a0d5d1cd20aa703a8da69ff67b7ed63cd8003007?color=5a5a5a) Eine Koordinatengleichung der Grundflächenebene ist somit gegeben als
Eine Koordinatengleichung der Grundflächenebene ist somit gegeben als  3. Schritt: Neigungswinkel ermitteln
3. Schritt: Neigungswinkel ermitteln
b)
Koordinaten von  ermitteln
ermitteln
![\(\begin{array}[t]{rll}
\overrightarrow{OB}&=&\overrightarrow{OA}+\overrightarrow{DC} \\[5pt]
&=&\pmatrix{3\\0\\4}+\pmatrix{0\\3\\-0,5} \\[5pt]
&=&\pmatrix{3\\3\\3,5}
\end{array}\)](https://mathjax.schullv.de/4f2a8812b19bba066c18583bd0eac2f7129da3b93c5f1f1f689e30f6d7eb0638?color=5a5a5a) Für die Koordinaten von
Für die Koordinaten von  gilt damit
gilt damit  Koordinaten von
Koordinaten von  ermitteln
Da alle Seiten der Grundfläche gleich lang sind, folgt für den Mittelpunkt
ermitteln
Da alle Seiten der Grundfläche gleich lang sind, folgt für den Mittelpunkt  Da die Höhe der Pyramide 3 Längeneinheiten beträgt, folgt mit dem normierten Vektor:
Für die Koordinaten der Spitze gilt somit
Da die Höhe der Pyramide 3 Längeneinheiten beträgt, folgt mit dem normierten Vektor:
Für die Koordinaten der Spitze gilt somit 
c)
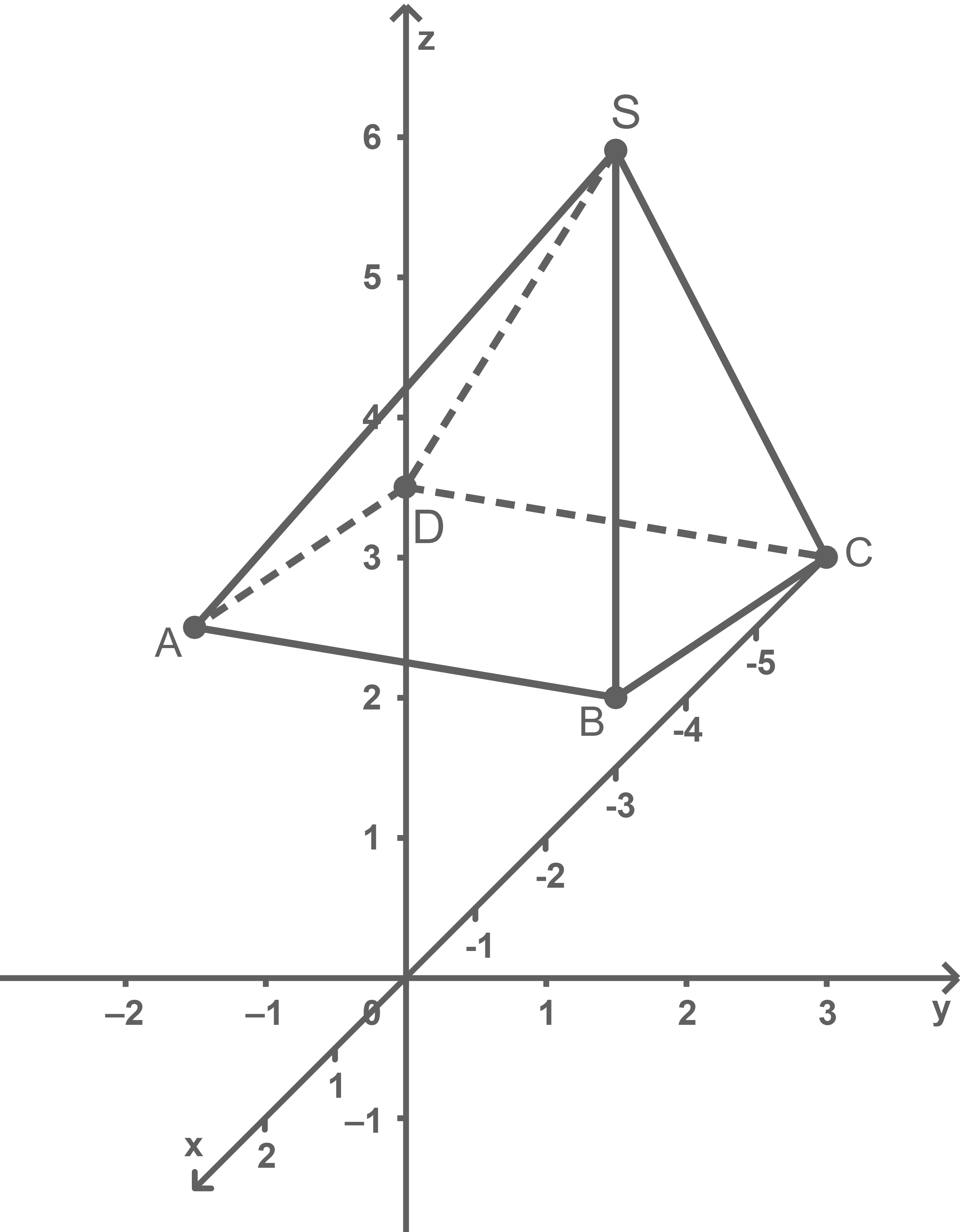
d)
Die Berechnung des Flächeninhalts  einer dreieckigen Dachfläche ergibt mit dem Kreuzprodukt im CAS:
einer dreieckigen Dachfläche ergibt mit dem Kreuzprodukt im CAS:



![\( \approx 5,1\;[\text{m}^2]\)](https://mathjax.schullv.de/12a60ca0fcdae9955b6e1e6ea45e6c97957404f832aa1724048329dc0f859450?color=5a5a5a)
e)
Da die Stützpfeiler senkrecht zum Boden stehen, folgt besipielsweise für die Fußpunkte von  und
und 



 Die maximale Länge einer Sitzbank beträgt damit
Die maximale Länge einer Sitzbank beträgt damit 
![\( \approx 4,24\;[\text{m}].\)](https://mathjax.schullv.de/9b99ab1dcbf6368b5a4c06e41561a7f5fd8d9c26dad1fab3f5ddde1539d5c912?color=5a5a5a)
f)
1. Schritt: Geradengleichung aufstellen
Mit  als Richtungsvektor und
als Richtungsvektor und  als Stützvektor folgt für die Geradengleichung der Sonnenstrahlen:
als Stützvektor folgt für die Geradengleichung der Sonnenstrahlen:
 2. Schritt: Schnittpunkt mit
2. Schritt: Schnittpunkt mit  -Ebene berechnen
-Ebene berechnen
![\(\begin{array}[t]{rll}
\pmatrix{1\\1\\5,05}+r\cdot\pmatrix{0\\1\\-2}&=&\pmatrix{x\\y\\0} \\[5pt]
\pmatrix{1\\1+r\\5,05-2r}&=&\pmatrix{x\\y\\0}
\end{array}\)](https://mathjax.schullv.de/dcff0b637ae93fb5bf6a885997e4b83422784bb0adb350a67fcb5fe8cccb6fd7?color=5a5a5a) Dieses LGS kann mit dem CAS gelöst werden. Es folgt
Dieses LGS kann mit dem CAS gelöst werden. Es folgt  und damit für die Koordinaten des Schnittpunkts
und damit für die Koordinaten des Schnittpunkts  Da die
Da die  -Koordinate größer als drei ist, liegt der Punkt außerhalb der Bodenfläche des Pavillons.
-Koordinate größer als drei ist, liegt der Punkt außerhalb der Bodenfläche des Pavillons.
g)
1. Schritt: Einen Normalenvektor der Dachfläche bestimmen


 2. Schritt: Einfallswinkel der Sonnenstrahlen berechnen
2. Schritt: Einfallswinkel der Sonnenstrahlen berechnen
 Mit Hilfe des CAS folgt somit
Mit Hilfe des CAS folgt somit 
2
a)
b)
Die Zufallsvariable  ist binomialverteilt mit Parametern
ist binomialverteilt mit Parametern  und
und  und gibt die Anzahl der Kunden an denen regionale Produkte wichtig sind. Mit dem CAS folgt dann:
und gibt die Anzahl der Kunden an denen regionale Produkte wichtig sind. Mit dem CAS folgt dann:





 Da die Sicherheitswahrscheinlichkeit
Da die Sicherheitswahrscheinlichkeit  betragen soll, folgt damit 154 als Mindestanzahl an Kunden die angeben, dass ihnen regionale Produkte wichtig sind.
betragen soll, folgt damit 154 als Mindestanzahl an Kunden die angeben, dass ihnen regionale Produkte wichtig sind.
c)
Ereignis  „Von 25 befragten Personen achten mindestens 13 und maximal 20 auf das Bio-Siegel.“
2. Schritt: Term zur Berechnung der Wahrscheinlichkeit angeben
Da
„Von 25 befragten Personen achten mindestens 13 und maximal 20 auf das Bio-Siegel.“
2. Schritt: Term zur Berechnung der Wahrscheinlichkeit angeben
Da  binomialverteilt mit
binomialverteilt mit  und
und  ist folgt:
ist folgt:

d)
Der Ansatz ist falsch, da in der Rechnung von der Annahme ausgegangen wird, dass es keine Abhängigkeit der beiden Ereignisse gibt. Das muss aber im Allgemeinen nicht gelten.