Teil C2

Die Bigband einer Schule nimmt anlässlich des 50-jährigen Jubiläums der Schule eine CD mit zehn Musikstücken auf. Vier dieser Stücke sind kurz, sechs lang. Diese CD wird in großer Anzahl hergestellt.

Bei der Jubiläumsfeier werden von einer dieser CDs in zufälliger Reihenfolge Stücke abgespielt, wobei jedes Stück auch mehrfach abgespielt werden kann.

Bestimme die Wahrscheinlichkeit dafür, dass die ersten drei abgespielten Stücke verschieden sind.

(2 BE)

Bestimme die Wahrscheinlichkeit folgender Ereignisse:
$A:$ „Unter zwölf abgespielten Stücken befinden sich genau fünf lange Stücke.“
$B:$ „Unter zwölf abgespielten Stücken befinden sich mehr lange als kurze Stücke.“

(4 BE)

Als die CDs vor der Jubiläumsfeier geliefert wurden, entdeckten die Mitglieder der Bigband unter den ersten 20 betrachteten CDs ein Exemplar mit fehlerhafter Hülle und befürchteten, dass mindestens $5\,\%$ aller Hüllen fehlerhaft sind. Sie planten deshalb die Durchführung eines Signifikanztests mit einem Signifikanzniveau von $10\,\%$ und der Nullhypothese „Der Anteil der fehlerhaften Hüllen ist kleiner als $5\,\%.$ “ Sollte das Ergebnis des Tests dafür sprechen, dass die Befürchtung zutrifft, wollten sie beim Hersteller einen Preisnachlass verlangen.

Gib eine Überlegung an, die zur Wahl der Nullhypothese geführt haben könnte, und begründe deine Angabe.

(2 BE)

Dem Test wurde eine Stichprobe von 150 CDs zugrunde gelegt.
Bestimme die zugehörige Entscheidungsregel.

(5 BE)

Angenommen, der beschriebene Test wird auf der Grundlage einer Stichprobe von 250 CDs durchgeführt. In diesem Fall wird die Nullhypothese abgelehnt, wenn mindestens 18 Hüllen fehlerhaft sind. Ermittle den Bereich, in dem der tatsächliche Anteil fehlerhafter Hüllen liegen müsste, damit die Wahrscheinlichkeit für den Fehler zweiter Art kleiner als $0,25$ ist.

(4 BE)

Bei der Jubiläumsfeier können die CDs sowohl zu einem Preis von 9 Euro pro Stück gekauft als auch bei einem Spiel gewonnen werden. Für das Spiel wird das abgebildete Glücksrad verwendet. Für einen Einsatz von einem Euro wird das Glücksrad dreimal gedreht. Nur wenn dabei genau zweimal der grau markierte Sektor getroffen wird, gewinnt man eine CD.
Die Größe des Öffnungswinkel dieses Sektors im Bogenmaß wird mit $b$ bezeichnet.

thüringen mathe abi 2020 teil c2 abbildung 1 kreisdiagramm

Zeige, dass die Wahrscheinlichkeit dafür, bei diesem Spiel eine CD zu gewinnen, mithilfe des Terms $\dfrac{3}{4\pi^2}b^2 - \dfrac{3}{8\pi^3}b^3$ berechnet werden kann.

(3 BE)

Es gibt Werte von $b,$ für die die Bigband bei mehrfacher Durchführung des Spiels im Mittel pro CD die gleichen Einnahmen erwarten könnte wie beim Verkauf der CD. Ermittle diese Werte.

(4 BE)

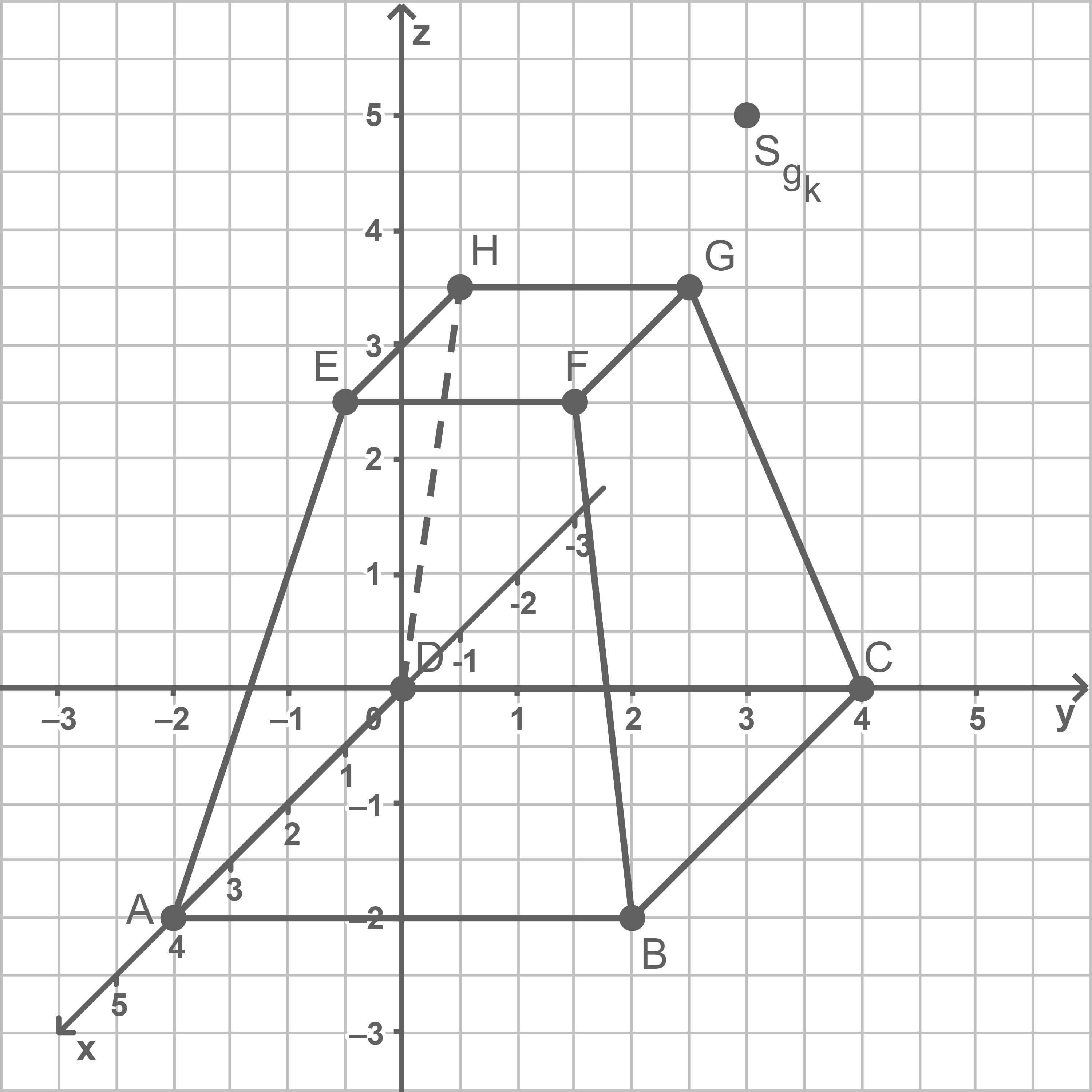
Von einem geraden, quadratischen Pyramidenstumpf $ABCDEFGH$ sind die Koordinaten der Eckpunkte $A(4\mid 0\mid 0),$ $B(4\mid 4\mid 0),$ $C(0\mid 4\mid 0),$ $D(0\mid 0\mid 0),$ $E(3\mid 1\mid 4)$ und $G(1\mid 3\mid 4)$ gegeben.

Stelle den Pyramidenstumpf in einem geeigneten Koordinatensystem dar. Gib die Koordinaten der Eckpunkte $F$ und $H$ an.

(4 BE)

Berechne den Flächeninhalt der Seitenfläche $ABFE.$

(3 BE)

Im Inneren des Pyramidenstumpfs gibt es einen Punkt $P(2 \mid 2 \mid z),$ der von allen Eckpunkten den gleichen Abstand besitzt.
Berechne die $z$ -Koordinate von $P.$

(3 BE)

Für jede reelle Zahl $k$ ist eine Gerade $g_k$ gegeben durch $g_k: \overrightarrow{x}= \pmatrix{2\\4\\6} +r \cdot \pmatrix{0\\-1\\k} (r\in\mathbb{R}).$

Begründe, dass alle Geraden $g_k$ parallel zur $yz$ -Ebene verlaufen. Gib den Abstand $d$ dieser Geraden zur $yz$ -Ebene an.

(2 BE)

Bestimme alle Werte $k,$ für die die Geraden $g_k$ mit dem Pyramidenstumpf gemeinsame Punkte besitzen.

(3 BE)

$P(\text{„keine Wiederholung“})$ $=\dfrac{10}{10}\cdot\dfrac{9}{10}\cdot\dfrac{8}{10}$ $=\dfrac{18}{25}$

Die Zufallsvariable $X$ gibt die Anzahl der langen Stücke an, und ist binomialverteilt mit Parametern $n=12$ und $p=\frac{6}{10}=0,6.$ Mit dem CAS folgt:

$P(A)=B_{12;0,6}(X=5)$ $\approx0,1009=10,09\,\%$

$P(B)=B_{12;0,6}(X\geq7)$ $= 1-B_{12;0,6}(X\leq6)$ $\approx0,6652 = 66,52\,\%$

Es soll vermieden werden, dass ein Preisnachlass verlangt wird, obwohl der Anteil der fehlerhaften Hüllen kleiner als $5\,\%$ ist.
Die Nullhypothese wird gewählt, um das Risiko für den Fehler, der vermieden werden soll, zu begrenzen.

Die Zufallsvariable $X$ gibt die Anzahl der CDs mit fehlerhaften Hüllen an und ist binomialverteilt mit Parametern $n=150$ und $p=0,05.$ Mit dem CAS folgt:

Rechenweg anzeigen

$B_{150;0,05}(X\leq k-1) \geq 0,9$

Systematisches Ausprobieren liefert:

$B_{150;0,05}(X\leq 10)\approx0,8678$

$B_{150;0,05}(X\leq 11)\approx0,9260$

Werden also bei mindestens $12$ CD's Fehler an der Hülle entdeckt, wird ein Preisnachlass verlangt.

Die Stichprobe umfasst $n=250$ CDs und besitzt den Ablehnungsbereich $\overline{A}=[18;250].$
Damit handelt es sich um einen rechtseitigen Signifikanztest und $k=17.$ Es soll $B_{250;p}(X\leq17)\leq0,25$ gelten. Systematisches Ausprobieren liefert:

$B_{250;0,081}(X\leq17)\approx0,26$

$B_{250;0,082}(X\leq17)\approx0,24997$

Somit muss $p\geq0,082$ gelten.

Die Wahrscheinlichkeit den grauen Sektor zu treffen, ergibt sich mit Hilfe des Bogenmaßes $b$ als $P=\frac{b}{2\pi}.$ Mit $n=3$ und $k=2$ folgt für die Wahrscheinlichkeit eine CD zu gewinnen:

$\pmatrix{n\\k}\cdot p^k\cdot(1-p)^{n-k}$ $=\pmatrix{3\\2}\cdot\left(\dfrac{b}{2\pi}\right)^2\cdot\left(1-\dfrac{b}{2\pi}\right)$ $=\dfrac{3}{4\pi^2}b^2-\dfrac{3}{8\pi^3}b^3$

Eine CD kostet im normalen Verkauf $9\,€,$ während eine Drehung des Glücksrads $1\,€$ kostet. Somit muss gelten:

$\dfrac{3}{4\pi^2}b^2-\dfrac{3}{8\pi^3}b^3=\dfrac{1}{9}$

Mit dem solve-Befehl des CAS folgt:

$\begin{array}[t]{rll} b_1&\approx&1,37 \\[5pt] b_2&\approx&6,03 \end{array}$

Pyramidenstumpf darstellen

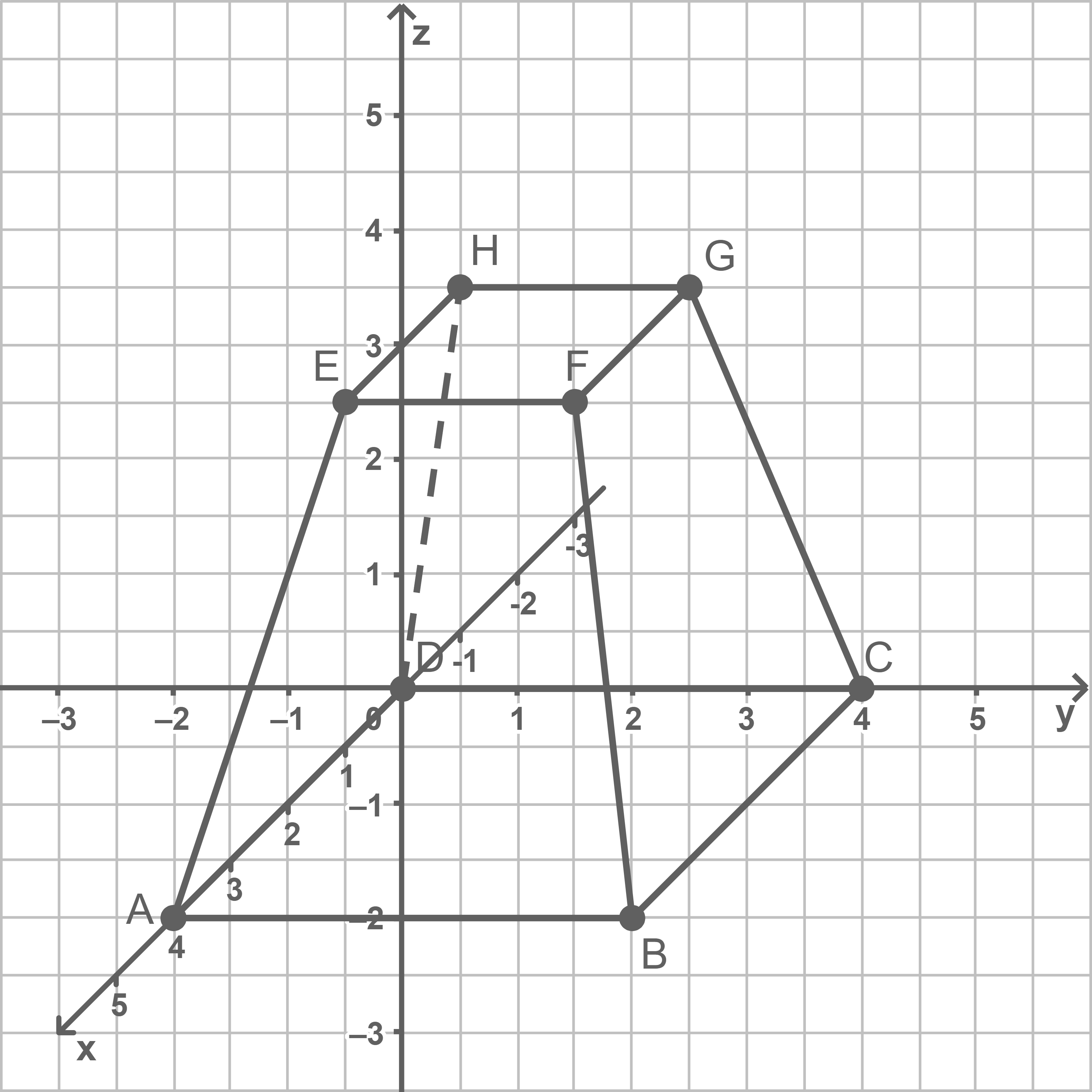Koordinaten angeben

$F(3\mid3\mid4)$

$H(1\mid1\mid4)$

Die Seitenflächen eines Pyramidenstumpfes sind Trapeze, für deren Flächeninhalt gilt:

$A=\dfrac{a+c}{2}\cdot h$
Für die Seitenlängen $a$ und $c$ folgt:

$a$ $= \sqrt{(4-4)^2+(4-0)^2+(0-0)^2}$ $= 4\;\text{LE}$

$c$ $= \sqrt{(3-3)^2+(3-1)^2+(4-4)^2}$ $= 2\;\text{LE}$

Die Höhe ergibt sich durch den Abstand der Mittelpunkte der Kanten $\overline{EF}$ und $\overline{AB}.$ Da diese beide in $y$ -Richtung liegen, folgt aus den Koordinaten der vier Eckpunkte direkt:

$M_{EF}(3\mid2\mid4)$

$M_{AB}(4\mid2\mid0)$

Somit gilt:

$h$ $= \vert\overrightarrow{M_{EF}M_{AB}}\vert$ $=\sqrt{(4-3)^2+(2-2)^2+(4-0)^2}$ $=\sqrt{17}$

Für den Flächeninhalt folgt damit:

$A=\dfrac{4+2}{2}\cdot\sqrt{17}$ $=3\cdot\sqrt{17}\;[\text{FE}]$

Der Punkt $P$ befinden sich von oben betrachtet in der Mitte des Pyramidenstumpfes. Somit wird nur folgende Gleichheit benötigt:

Rechenweg anzeigen

$z = \dfrac{5}{4}$

Die Koordinaten von $P$ ergeben sich damit als:

$P\left(2\mid2\mid\frac{5}{4}\right)$

Da der Richtungsvektor der Geradenschar die $x$ -Koordinate Null besitzt, verlaufen alle Geraden, parallel zur $yz$ -Ebene.
Der Abstand zu dieser beträgt $d=2,$ was aus der $x$ -Koordinate des Ortsvektors folgt.

Die Lage des Stützsvektors $\overrightarrow{OS_{g_k}}$ der Geradenschar in der Hilfsskizze zeigt, dass genau die Geraden der Schar keine gemeinsamen Punkte mit dem Pyramidenstumpf haben, die über der Kante $\overline{EH}$ verlaufen. Gleichsetzen der Geradenschar mit der Gerade, auf der die Kante $\overline{EH}$ liegt, liefert:

$\pmatrix{2\\4\\6}+r\cdot\pmatrix{0\\-1\\k}$ $=\pmatrix{3\\1\\4}+s\cdot\pmatrix{-2\\0\\0}$

Es ergibt sich folgendes Gleichungssystem:

$\begin{array}{lrll} \text{I}\quad&2&=& 3 -2s \\ \text{II}\quad&4-r&=&1 &\quad \\ \text{III}\quad&6+r\cdot k&=&4 &\quad \\ \end{array}$

Lösen dieses Gleichungssystems mit dem CAS liefert für $k:$

$k=-\dfrac{2}{3}$

Alle Geraden der Geradenschar mit $k\leq-\frac{2}{3}$ haben somit gemeinsame Punkte mit dem Pyramidenstumpf.