Teil C2

In einer repräsentativen Online-Befragung zum Radfahrverhalten im Jahr 2021 gaben $45\,\%$ aller Radfahrer an, zum Schutz während der Fahrt einen Helm zu tragen. Der Anteil an E-Bike-Fahrern unter allen Radfahrern betrug $14\,\%.$

Eine Schülergruppe plant eine Verkehrsbeobachtung und nutzt dazu die Angaben der Online-Befragung und das Modell der Binomialverteilung. Die relativen Häufigkeiten werden dabei als Wahrscheinlichkeiten interpretiert.

Nenne zwei Voraussetzungen, die von der Schülergruppe beachtet werden müssen, damit die Anzahl der E-Bike-Fahrer als binomialverteilt angesehen werden kann.

(2 BE)

Berechne die Wahrscheinlichkeit folgender Ereignisse:

$A:=$

„Unter den ersten 50 beobachteten Radfahrern befinden sich weniger als vier E-Bike-Fahrer.“

$B:=$

„Die Anzahl der Helmträger bei 40 Radfahrern ist um mindestens fünf größer als der Erwartungswert.“

(5 BE)

Beschreibe im Sachzusammenhang ein Ereignis $C,$ dessen Wahrscheinlichkeit durch

$P(C)$ $=0,45$ $\cdot\left(\pmatrix{39\\9} \cdot 0,45^9 \cdot 0,55^{30}\right)$

berechnet werden kann.

(3 BE)

Gegeben ist folgende Ungleichung:

$\dfrac{2 \cdot \sqrt{n \cdot 0,14 \cdot(1-0,14)}}{n}\lt0,1$

Ermittle die Lösung der Ungleichung.
Erläutere die Bedeutung der Ungleichung und ihrer Lösung im Sachzusammenhang.

(3 BE)

Die Wahrscheinlichkeit, dass ein Helm getragen wird, ist bei E-Bike-Fahrern doppelt so groß wie bei Fahrern von nicht motorisierten Fahrrädern.

Ermittle mithilfe eines Baumdiagramms oder einer Vierfeldertafel die Wahrscheinlichkeit $p,$ dass ein beliebiger Radfahrer ein E-Bike nutzt und keinen Helm trägt.
$\big[$ Kontrollergebnis: $p \approx 0,0295 \big]$

(4 BE)

Ermittle die Anzahl der Radfahrer, die mindestens beobachtet werden müssen, um mit einer Wahrscheinlichkeit von mindestens $90\,\%$ mehr als zehn E-Bike-Fahrer ohne Helm zu erfassen.

(3 BE)

Die Bundesanstalt für Straßenwesen führt jährlich deutschlandweit Verkehrsbeobachtungen durch. Die Beobachtungen des Jahres 2021 umfassten 16199 Radfahrer und ergaben, dass über alle Altersgruppen hinweg $31,7\,\%$ aller Radfahrer einen Helm trugen.

https://www.bast.de (14.11.2022)

Berechne das $2 \sigma$ -Konfidenzintervall für den Anteil der Helmträger für diese Verkehrsbeobachtungen.
Beurteile das Ergebnis der Online-Befragung zum Radfahrverhalten aus dem Jahr 2021 anhand des von Ihnen ermittelten Konfidenzintervalls.

(5 BE)

Für alle reellen Zahlen $a$ ist die Schar von Geraden $g_a$ gegeben durch:

$\overrightarrow{x}$ $=\pmatrix{3\\-2\\1}$ $+r$ $\cdot \pmatrix{2-a\\a\\2a-1} \quad(r \in \mathbb{R})$

Zeige, dass die Gerade $g_{-4}$ die $z$ -Achse schneidet und berechne die Größe des Schnittwinkels.

(4 BE)

Weise nach, dass sich die Geraden $g_{-4}$ und $g_{\frac{3}{4}}$ orthogonal schneiden.

(2 BE)

Bestimme die Gerade der Schar $g_a,$ die parallel zu $y$ - $z$ -Ebene liegt.

(2 BE)

Gegeben ist die Ebene $\varepsilon$ durch die Gleichung $x-3y+2z=11.$

Zeige, dass alle Geraden der Schar $g_a$ in der Ebene $\varepsilon$ liegen.

(2 BE)

Die Schnittpunkte der Ebene $\varepsilon$ mit den Koordinatenachsen bilden die Grundfläche einer Pyramide, deren Spitze der Koordinatenursprung ist.
Ermittle das Volumen und die Höhe dieser Pyramide.

(5 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Es muss eine klare Unterteilung aller Fahrräder in E-Bike und kein E-Bike geben und die Auswahl der Radfahrer muss zufällig erfolgen.

$P(A)$ $= B_{50 ; 0,14}(X \lt 4)$ $=B_{50 ; 0,14}(X \leq 3) \approx 0,0670$

Der Erwartungswert ergibt sich als $\mu$ $= n \cdot p$ $= 40\cdot0,45$ $= 18.$ Damit folgt:

$P(B)=B_{40 ; 0,45}(X \geq 23)\approx 0,0767$

Von 40 Radfahrern trägt der erste einen Helm und unter den anderen 39 sind genau neun weitere Radfahrer mit Helm.

1. Schritt: Lösung der Ungleichung ermitteln

Auflösen der Ungleichung nach $n$ mit dem solve-Befehl des CAS liefert:

$n\gt48$

2. Schritt: Erläuterung der Ungleichung im Sachzusammenhang

Es müssen mindestens 49 Radfahrer beobachtet werden, damit die relative Häufigkeit des Anteils der E-Bike-Fahrer mit einer Wahrscheinlichkeit von $95 \%$ um weniger als $0,1$ von $p=0,14$ abweicht.

Für die Berechnung der Wahrscheinlichkeit, dass jemand der kein E-Bike fährt einen Helm trägt, ergibt sich:

$0,14\cdot2x$ $+0,86\cdot x=0,45$

Auflösen dieser Gleichung nach $x$ mit Hilfe des CAS liefert:

$x\approx 0,395$

Lösungsweg A: Baumdiagramm

$E:$ Ein zufällig ausgewählter Radfahrer fährt ein E-Bike.

$H:$ Ein zufällig ausgewählter Radfahrer trägt einen Helm.

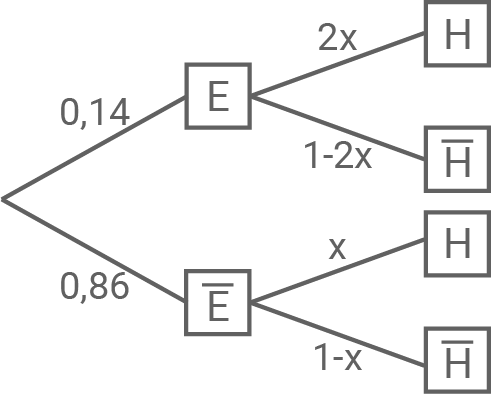Für die Wahrscheinlichkeit, dass ein beliebiger Radfahrer ein E-Bike nutzt und keinen Helm trägt folgt damit mit dem ungerundeten Wert von $x:$

$P(E\cap\overline{H})$ $=0,14\cdot (1-2x) \approx 0,0295$

Lösungsweg B: Vierfeldertafel

$E:$ Ein zufällig ausgewählter Radfahrer fährt ein E-Bike.

$H:$ Ein zufällig ausgewählter Radfahrer trägt einen Helm.

	$\color{#fff}{H}$	$\color{#fff}{\overline{H}}$
$\color{#fff}{E}$	$0,14\cdot2x$	$0,14\cdot(1-2x)$	$0,14$
$\color{#fff}{\overline{E}}$	$0,86\cdot x$	$0,86\cdot (1-x)$	$0,86$
	$0,45$	$0,55$	$1$

Für die Wahrscheinlichkeit, dass ein beliebiger Radfahrer ein E-Bike nutzt und keinen Helm trägt folgt damit mit dem ungerundeten Wert von $x:$

$P(E\cap\overline{H})$ $=0,14\cdot (1-2x) \approx 0,0295$

Es wird die binomialverteilte Zufallsvariable mit $p=0,0295$ betrachtet. Für $n=519$ liefert der CAS:

$P(X\geq11)$ $\approx 0,8993 = 89,93 \%$

Für $n=520$ folgt mit dem CAS:

$P(X\geq11)$ $\approx 0,9006 = 90,06 \%$

Es müssen also mindestens 520 Radfahrer beobachtet werden um mit einer Wahrscheinlichkeit von mindestens $90 \%$ mehr als zehn E-Bike-Fahrer ohne Helm zu erfassen.

$2\sigma$ -Konfidenzintervall berechnen

Mit $n=16199$ und $h=0,317$ wird die folgende Formel zur Berechnung des $2\sigma$ -Konfidenzintervalles benutzt:

$\vert p-h\vert \leq 2 \cdot \dfrac{\sqrt{p \cdot(1-p)}}{\sqrt{n}}$

Auflösen nach $p$ mit dem CAS liefert gerundet $0,310\lt p\lt0,324.$ Das Konfidenzintervall ist damit ungefähr gegeben durch $[0,310;0,324].$

Ergebnis der Online-Befragung beurteilen

Die Online-Befragung liefert, dass $45\%$ der Radfahrer zum Schutz während der Fahrt einen Helm tragen. Da das nicht im Konfidenzintervall liegt, ist das Umfrageergebnis nicht verträglich mit diesem.

Schnittpunkt zeigen

Die Geradengleichung von $g_{-4}$ ist gegeben durch:

$g_{-4}:\overrightarrow{x}$ $=\pmatrix{3\\-2\\1}$ $+r$ $\cdot \pmatrix{2-(-4)\\-4\\2\cdot(-4)+1}$ $= \pmatrix{3\\-2\\1}$ $+r$ $\cdot \pmatrix{6\\-4\\-9}$

Gleichsetzen mit einem allgemeinen Punkt der $z$ -Achse liefert:

$\pmatrix{0\\0\\z}=\pmatrix{3\\-2\\1}$ $+r$ $\cdot \pmatrix{6\\-4\\-9}$

Das LGS kann mit dem CAS gelöst werden. Aus den ersten beiden Zeilen $0=3+6r$ und $0=-2-4r$ folgt:

$r=-\dfrac{1}{2}$

Einsetzen in die dritte Zeile ergibt:

$z=1+\dfrac{1}{2}\cdot 9 = \dfrac{11}{2}$

Somit schneidet $g_{-4}$ die $z$ -Achse im Punkt mit den Koordinaten $(0\mid0\mid\frac{11}{2}).$

Schnittwinkel berechnen

Für den Schnittwinkel $\alpha$ der beiden Geraden gilt:

$\cos(\alpha)=\dfrac{\left\vert\pmatrix{6\\-4\\-9}\circ\pmatrix{0\\0\\1}\right\vert}{\left\vert\pmatrix{6\\-4\\-9}\right\vert\cdot\left\vert\pmatrix{0\\0\\1}\right\vert}$

Mit dem solve-Befehl des CAS folgt der Schnittwinkel $\alpha\approx38,7^\circ.$

Der Richtungsvektor der Gerade $g_{\frac{3}{4}}$ ist gegeben als:

$\pmatrix{2-\frac{3}{4}\\\frac{3}{4}\\2\cdot\frac{3}{4}-1}$ $= \pmatrix{\frac{5}{4}\\\frac{3}{4}\\\frac{2}{4}}$

Für die Berechnung des Skalarproduktes kann auch der mit vier multiplizierte Vektor benutzt werden:

$4\cdot\pmatrix{\frac{5}{4}\\\frac{3}{4}\\\frac{2}{4}}=\pmatrix{5\\3\\2}$

Es folgt:

$\pmatrix{6\\-4\\-9}\circ\pmatrix{5\\3\\2}$ $= 30-12-18$ $= 0$

Da der Stützpunkt der Geradenschar von $a$ unabhängig ist, laufen alle Geraden der Schar durch diesen Punkt und die Geraden $g_{-4}$ und $g_{\frac{3}{4}}$ schneiden sich somit orthogonal.

Damit eine Gerade parallel zur $y$ - $z$ -Ebene liegt, muss die $x$ -Koordinate des Richtungsvektors Null sein. Aus der $x$ -Koordinaten des Richtungsvektors von $g_a$ folgt:

$\begin{array}[t]{rll} 2-a&=&0 \\[5pt] 2&=&a \end{array}$

Somit liegt $g_2$ parallel zur $y$ - $z$ -Ebene.

Aus der Geradengleichung von $g_a$ folgt:

$\begin{array}[t]{rll} x&=&3+r\cdot(2-a) \\[5pt] y&=&-2+r\cdot a \\[5pt] z&=&1+r\cdot(2a-1) \end{array}$

Einsetzen in die Ebenengleichung von $\varepsilon$ liefert:

Rechenweg anzeigen

$11=11$

Somit liegen alle Geraden der Schar $g_a$ in der Ebene $\varepsilon.$

Schnittpunkte bestimmen

Einsetzen der allgemeinen Punkte $\pmatrix{x\\0\\0},\pmatrix{0\\y\\0}$ und $\pmatrix{0\\0\\z}$ der drei Koordinatenachsen in die Ebenengleichung liefert für die Koordinaten der jeweiligen Schnittpunkte:

$P_x(11\mid0\mid0),P_y(0\mid-\frac{11}{3}\mid0)$ und $P_z(0\mid0\mid\frac{11}{2}).$

Höhe und Volumen der Pyramide berechnen

Für den Flächeninhalt der dreieckigen Grundfläche folgt mit dem Kreuzprodukt im CAS:

$G$ $= \dfrac{1}{2}\cdot\vert\overrightarrow{P_yP_z}\times\overrightarrow{PyP_x}\vert$ $= \dfrac{1}{2}\cdot\left\vert\pmatrix{11\\\frac{11}{2}\\0}\times\pmatrix{0\\\frac{11}{2}\\\frac{11}{3}}\right\vert$ $\approx 37,73\;[\text{FE}]$

Der Betrag des Normalenvektors der Ebene $\varepsilon$ beträgt:

$\vert\overrightarrow{n}\vert$ $= \sqrt{1^2+(-3)^2+2^2}$ $= \sqrt{14}$

Einsetzen des Koordinatenursprungs in die Hessesche Normalform von $\varepsilon$ liefert für die Höhe der Pyramide:

$h$ $= \left\vert\dfrac{0-3\cdot0+2\cdot0-11}{\sqrt{14}}\right\vert$ $= \dfrac{11}{\sqrt{14}}\;[\text{LE}].$

Mit dem ungerundeten Wert von $G$ folgt für das Volumen der Pyramide somit:

$V$ $= \dfrac{1}{3}\cdot G\cdot h$ $=\dfrac{1}{3}$ $\cdot\dfrac{1}{2}$ $\cdot\left\vert\pmatrix{11\\\frac{11}{2}\\0}\times\pmatrix{0\\\frac{11}{2}\\\frac{11}{3}}\right\vert$ $= \dfrac{1331}{36}\;[\text{VE}]$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?