Teil C1

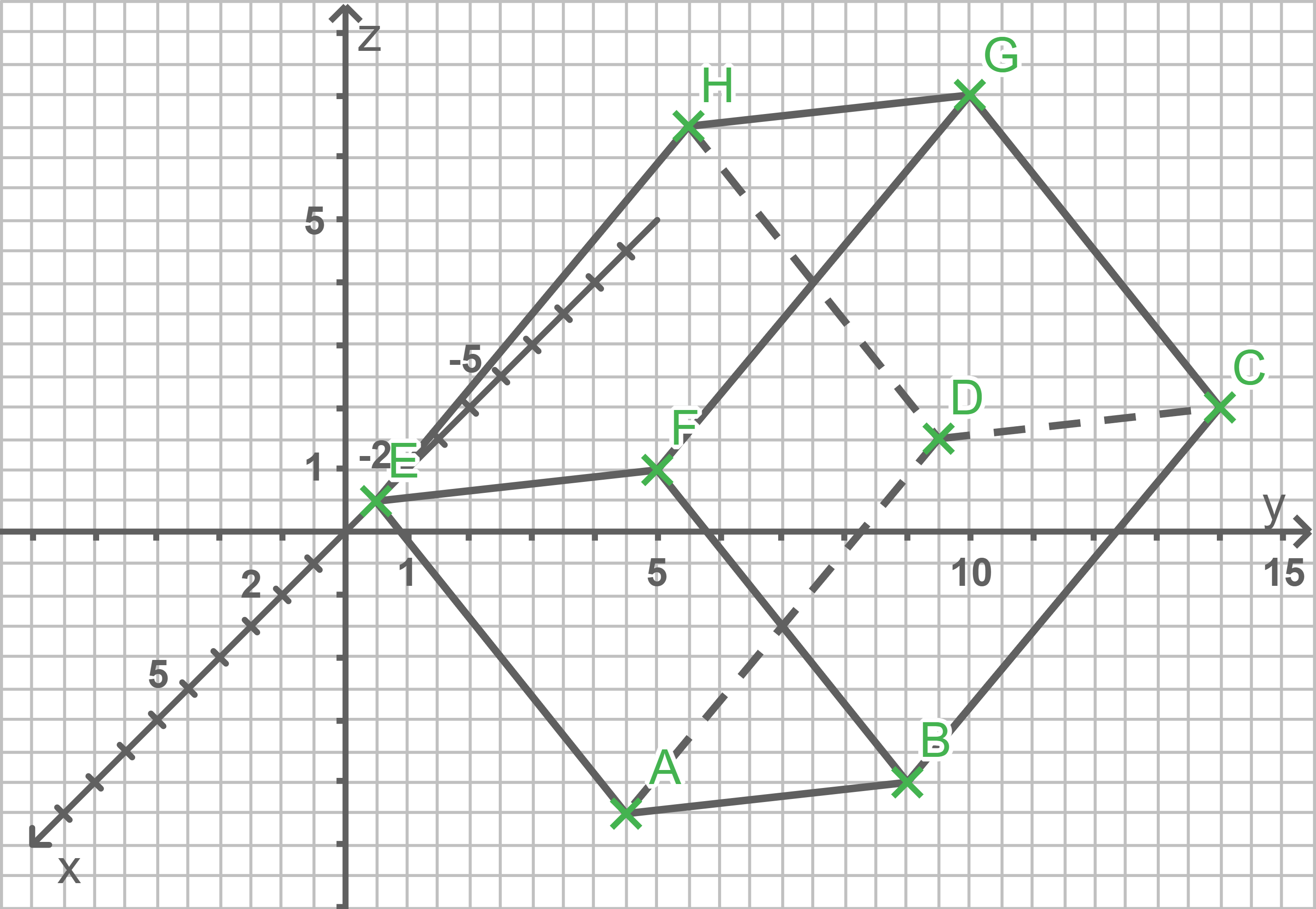
In Apolda wurde 2009 eine Schach-Skulptur mit Figuren im Bauhausstil nach Entwürfen von Prof. Josef Hartwig aus dem Jahr 1923 auf einer Rasenfläche aufgestellt. Nur eine Seitenfläche der würfelförmigen Skulptur ist vollständig sichtbar.

Schachbrett mit geometrischen Figuren in einer ungewöhnlichen Perspektive.

Eine Schülergruppe plant für eine Rasenfläche auf dem Schulgelände eine ähnliche Skulptur. Mit dynamischer Geometriesoftware wird ein Würfel $ABCDEFGH$ mit $A(-1\mid 4 \mid -5),$ $E(1\mid 1 \mid 1),$ $F(4\mid 7 \mid 3),$ $G(-2\mid 9 \mid 6)$ und $H(-5\mid 3 \mid 4)$ entworfen.
Die $xy$ -Ebene stellt die Rasenfläche dar.
Eine Längeneinheit entspricht $20 \,\text{cm}$ in der Wirklichkeit.

Vervollständige die graphische Darstellung des Würfels in der Abbildung. Ermittle die Koordinaten der Eckpunkte $B,$ $C$ und $D.$

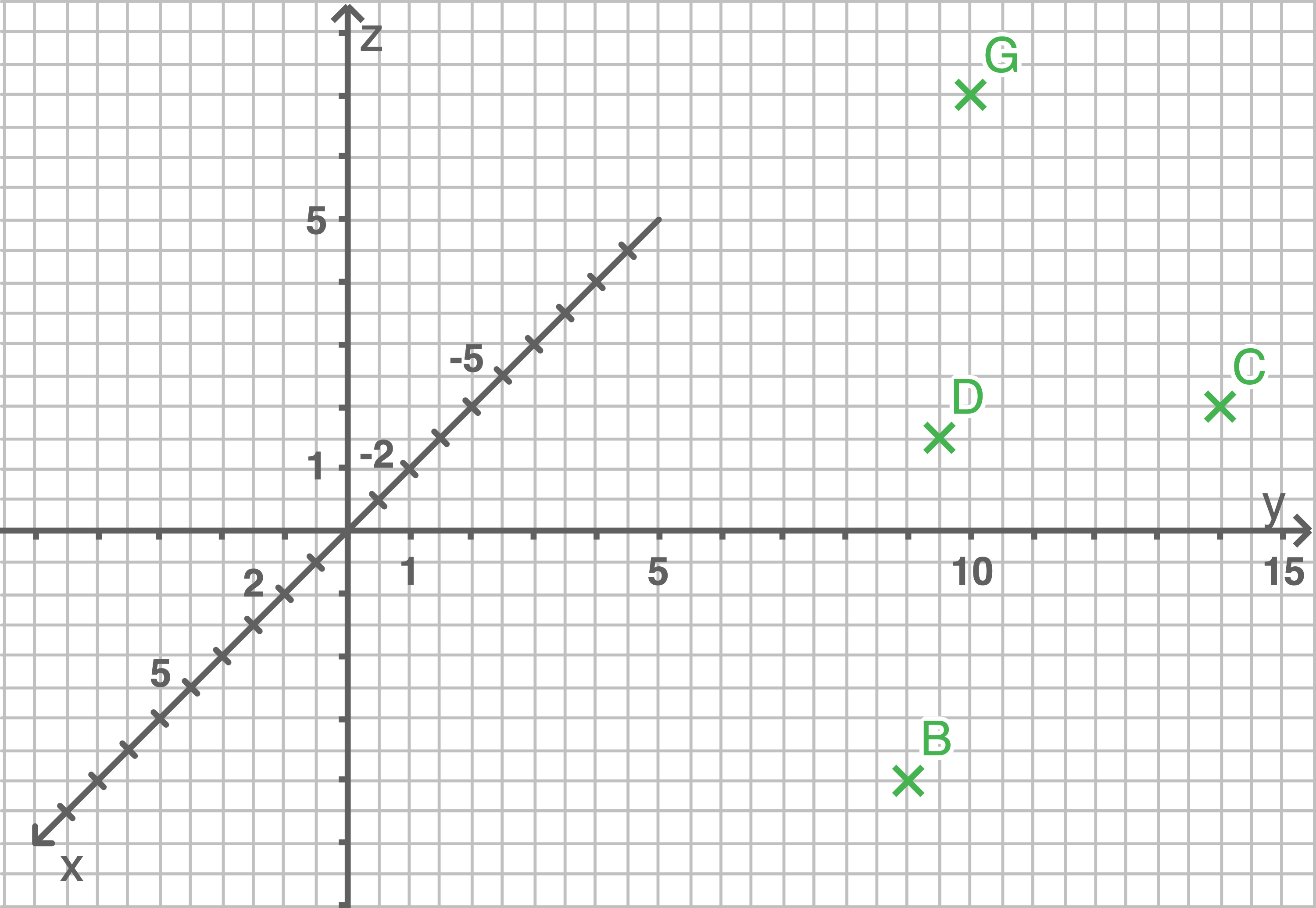
thüringen mathe abi 2020 teil c1 abbildung 1

(6 BE)

Auf die Fläche, die dem Quadrat $EFGH$ entspricht, soll das Schachbrett ohne Rand aufgezeichnet werden.

Berechne den Flächeninhalt des Schachbretts in Quadratmeter.

(2 BE)

Berechne die Größe des Winkels, unter dem die Fläche mit dem Schachbrett gegenüber der Rasenfläche geneigt ist.

(3 BE)

Die Skulptur auf dem Schulgelände soll nach dem Eingraben entlang der Rasenkanten mit Aluminiumleisten eingefasst werden.
Beschreibe eine mögliche Vorgehensweise zur Berechnung der Gesamtlänge dieser Einfassung.

(3 BE)

Ausgehend vom Mittelpunkt des Schachbretts soll die Skulptur senkrecht zur Rasenfläche bis zur gegenüberliegenden Fläche durchbohrt werden.
Zeige, dass eine durchgeführte Bohrung ca. $1,63 \,\text{m}$ lang sein würde.

(6 BE)

Die Schüler planen in der Nähe der Skulptur, einen Baum zu pflanzen.
Der Mindestabstand zur Skulptur soll zwei Meter betragen.
Der Standort des Baums wird durch den Punkt $P(-8 \mid -6 \mid 0)$ festgelegt.
Der Baumstamm soll senkrecht auf der Rasenfläche stehen und sein Durchmesser wird vernachlässigt.

Untersuche, ob für diesen Standort der Mindestabstand des Baumstamms von der Kante der Skulptur, die im Modell $\overline{EH}$ entspricht, gewährleistet ist.

(6 BE)

Laut einer repräsentativen Umfrage des Meinungsforschungsinstitutes forsa im Juli 2017 sind $52\,\%$ aller Deutschen über 18 Jahre für ein Tempolimit von $130 \,\text{km/h}$ auf Autobahnen.
Im Rahmen einer Seminarfacharbeit führten Schüler in ihrer Stadt eine Befragung zu diesem Thema durch. Für die Auswertung der Daten soll das Modell der Binomialverteilung unter Verwendung des Ergebnisses der forsa-Umfrage genutzt werden.

Gib drei Bedingungen an, die die Schüler bei der Planung der Befragung beachten mussten.

(3 BE)

Berechne für die Befragung der Schüler die Wahrscheinlichkeit folgender Ereignisse, wenn 200 Deutsche über 18 Jahre zufällig befragt wurden:

$A:$ „Mindestens 90 Befragte sind für das Tempolimit.“
$B:$ „Die Zahl der Befürworter des Tempolimits weicht um höchstens die Standardabweichung vom Erwartungswert ab.“

(5 BE)

Ermittle die Anzahl der Personen, die von den Schülern mindestens befragt werden müssten, damit sich mit einer Wahrscheinlichkeit von mindestens $99\,\%$ mindestens 100 von ihnen für ein Tempolimit aussprechen.

(3 BE)

Die Schüler zweifeln an, dass das Umfrageergebnis von 2017 noch immer gültig ist. Sie wollen deshalb auf der Grundlage ihrer Befragung mit 200 Personen einen zweiseitigen Signifikanztest durchführen.
Sie legen vorab fest, dass sie dem Umfrageergebnis nicht mehr glauben, wenn sich weniger als 90 oder mehr als 120 der Befragten für ein Tempolimit aussprechen.

Berechne die Irrtumswahrscheinlichkeit dieses Tests. Interpretiere dein Ergebnis im Sachzusammenhang.

(4 BE)

$\overrightarrow{OB}$ $= \overrightarrow{OA} + \overrightarrow{EF}$ $= \pmatrix{-1\\4\\-5}+\pmatrix{4-1\\7-1\\3-1}$ $= \pmatrix{2\\10\\-3}$

$\overrightarrow{OC}$ $= \overrightarrow{OB} + \overrightarrow{EH}$ $= \pmatrix{2\\10\\-3}+\pmatrix{-5-1\\3-1\\4-1}$ $= \pmatrix{-4\\12\\0}$

$\overrightarrow{OD}$ $= \overrightarrow{OC} + \overrightarrow{FE}$ $= \pmatrix{-4\\12\\0}+\pmatrix{1-4\\1-7\\1-3}$ $= \pmatrix{-7\\6\\-2}$

Die gesuchten Koordinaten der Eckpunkte $B,C$ und $D$ ergeben sich somit als $B=(2\mid10\mid-3),C=(-4\mid12\mid0)$ und $D=(-7\mid6\mid-2).$

Für die Länge der Seiten des Würfels gilt:

$\vert\overrightarrow{EF}\vert$ $= \sqrt{(4-1)^2+(7-1)^2+(3-1)^2}$ $= 7\;[\text{LE}]$

Da $1\;\text{LE} =\;20\;\text{cm}$ $= 0,2\;\text{m}$ entspricht, folgt für den Flächeninhalt des Schachbretts:

$A = (7\cdot0,2)^2 = 1,96\;[\text{m}^2]$

Ein Normalenvektor der Ebene, in der die Seite mit dem Schachbrett liegt, ergibt sich wie folgt:

$\overrightarrow{n_1} = \overrightarrow{EA} = \pmatrix{2\\-3\\6}$

Mit $\overrightarrow{n_2}=\pmatrix{0\\0\\1}$ als Normalenvektor der $xy$ -Ebene folgt weiter:

Rechenweg anzeigen

$\alpha \approx 31^{\circ}$

Zunächst werden die Spurpunkte der Seitenkanten $\overline{EA},\overline{FB},\overline{HD}$ und $\overline{GC}$ mit der $xy$ -Ebene berechnet. Die Summe der Abstände dieser Punkte zueinander ergibt die Gesamtlänge der Einfassung.

Der Mittelpunkt $M$ des Schachbretts ergibt sich wie folgt:

$M_{\overline{EF}}$ $= \overrightarrow{OE} + \dfrac{1}{2}\cdot\overrightarrow{EF}$ $=\pmatrix{1\\1\\1}+\dfrac{1}{2}\cdot\pmatrix{3\\6\\2}$ $=\pmatrix{\frac{5}{2}\\4\\2}$

$M=\overrightarrow{OM_{\overline{EF}}}+\dfrac{1}{2}\cdot\overrightarrow{EH}$ $=\pmatrix{\frac{5}{2}\\4\\2}+\dfrac{1}{2}\cdot\pmatrix{-6\\2\\3}$ $= \pmatrix{-\frac{1}{2}\\5\\ \frac{7}{2}}$

Die Gerdengleichung der Bohrung ergibt sich somit als:

$g:\overrightarrow{x}$ $=\pmatrix{-\frac{1}{2}\\5\\ \frac{7}{2}}+r\cdot\pmatrix{0\\0\\1}$

Mit Hilfe der Vektoren ihrer Kanten als Spannvektoren folgt für die Ebenengleichung der unteren Fläche:

$E:\overrightarrow{x}$ $=\overrightarrow{OA}+\overrightarrow{AB}+\overrightarrow{AD}$ $=\pmatrix{-1\\4\\-5}$ $+s\cdot\pmatrix{3\\6\\2}$ $+t\cdot\pmatrix{-6\\2\\3}$

Gleichsetzen von $g$ und $E$ liefert folgendes Gleichungssystem:

$\begin{array}{lrll} \text{I}\quad&-\dfrac{1}{2}&=& -1+3s-6t&\quad \\ \text{II}\quad&5&=&4+6s+2t &\quad \\ \text{III}\quad&\dfrac{7}{2}+r&=& -5+2s+3t &\quad \\ \end{array}$

Lösen des Gleichungssystems mit dem CAS liefert:

$\begin{array}[t]{rll} r&=&-\dfrac{49}{6} \\[5pt] s&=&\dfrac{1}{6} \\[5pt] t&=&0 \end{array}$

Einsetzen von $r$ in $g$ oder $s$ und $t$ in $E$ liefert die folgenden Koordinaten für den Bohrpunkt in der unteren Fläche:

$K\left(-\frac{1}{2}\mid5\mid-\frac{14}{3}\right)$

Für die Länge der Bohrung folgt somit:

$d$ $= \vert\overrightarrow{MK}\vert\cdot0,2$ $\approx8,17\cdot0,2$ $\approx1,63\;[\text{m}]$

Mit Hilfe eines Normalenvektors der $xy$ -Ebene folgt für eine Ebenengleichung der Ebene, die durch die Kante $\overline{EH}$ verläuft und senkrecht zur $xy$ -Ebene liegt:

$E:\overrightarrow{x}$ $=\pmatrix{1\\1\\1}$ $+u\cdot\pmatrix{-6\\2\\3}$ $+v\cdot\pmatrix{0\\0\\1}$

Als ein Normalenvektor der Ebene ergibt sich:

$\overrightarrow{n}$ $=\pmatrix{-6\\2\\3}\times\pmatrix{0\\0\\1}$ $=\pmatrix{2\\6\\0}$

Für die Geradengleichung der Lotgeraden durch $P$ folgt damit:

$g:\overrightarrow{x}$ $=\pmatrix{-8\\-6\\0}+w\cdot\pmatrix{2\\6\\0}$

Gleichsetzen von $g$ und $E$ liefert folgendes Gleichungssystem:

$\begin{array}{lrll} \text{I}\quad&-8+2w&=&1-6u \\ \text{II}\quad&-6+6w&=& 1+2u \\ \text{III}\quad&0&=& 1+3u+v \\ \end{array}$

Mit Hilfe des CAS ergibt sich folgende Lösung:

$\begin{array}[t]{rll} w&=&\dfrac{3}{2} \\[5pt] u&=&1 \\[5pt] v&=&-4 \end{array}$

Einsetzen von $w$ in $g$ liefert:

$\overrightarrow{OL}$ $=\pmatrix{-8\\-6\\0}+\dfrac{3}{2}\cdot\pmatrix{2\\6\\0}$ $=\pmatrix{-5\\3\\0}$

Der Abstand zwischen dem Baum und der Kante der Skulptur ergibt sich durch den Betrag von $\overrightarrow{LP}:$

$\vert\overrightarrow{LP}\vert$ $=\sqrt{(-8+5)^2+(-6-3)^2+(0-0)^2}$ $=3\sqrt{10}\;\text{LE}$

Damit folgt:

$3\sqrt{10}\cdot0,2\approx1,9\lt2\;[\text{m}]$

Der Mindestabstand wird somit nicht eingehalten.

Mögliche Bedingungen:

Die Befragten müssen volljährige deutsche Staatsbürger sein
Es darf nur zwei Antwortmöglichen geben
Die Befragten müssen unabhängig voneinander antworten
Die Auswahl der Befragten erfolgt zufällig
Keine Mehrfachbefragung
Die Stichprobe muss einen großen Umfang haben, um repräsentativ zu sein

Die Zufallsvariable $X$ gibt die Anzahl der Befragten an, die für das Tempolimit sind und ist binomialverteilt mit Parametern $n=200$ und $p=0,52.$ Mit dem CAS folgt:

$P(A)=B_{200;0,52}(X\geq90)$ $=1-B_{200;0,52}(X\leq89)\approx0,9800$ $= 98\,\%$

Für den Erwartungswert und die Standardabweichung von $X$ gilt:

$E(X)=0,52\cdot200$ $=104$

$\sigma(X)$ $=\sqrt{200\cdot0,52\cdot(1-0,52)}$ $\approx7,06$

Damit folgt:

$P(B)$ $= B_{200;0,52}(97\leq X\leq111)$ $= B_{200;0,52}(X\leq111)$ $-B_{200;0,52}(X\leq96)$ $\approx0,7116 = 71,16\,\%$

Gesucht ist ein passendes $n,$ für das gilt:

Rechenweg anzeigen

$B_{n;0,52}(X\leq99) \leq 0,01$

Systematisches Ausprobieren liefert:

$B_{224;0,52}(X\leq99)\approx0,0116$

$B_{225;0,52}(X\leq99)\approx0,0098$

Es müssen somit mindestens $225$ Personen befragt werden.

Für die Irrtumswahrscheinlichkeit folgt:

Rechenweg anzeigen

$a \approx 2,96\,\%$

Mit einer Wahrscheinlichkeit von knapp unter $3\,\%$ nehmen die Schüler somit an, dass der Anteil der Beführworter des Tempolimits nicht mehr bei $52\,\%$ liegt, obwohl das immernoch der Fall ist.