SchulLV Logo
Lerninhalte in Chemie
Abi-Aufgaben LF
Basiswissen
Inhaltsverzeichnis

Säuren- und Basenstärke

In diesem Kapitel wollen wir uns mit dem Begriff der Säuren- bzw. Basenstärke beschäftigen. Dazu wollen wir Fragen klären, wie beispielsweise:

  • Was ist die Bedeutung des Begriffs Stärke im Kontext zu Säuren und Basen?
  • Welche Bedeutung hat der Begriff der Stärke für die Chemie von Säuren und Basen?
Wir wollen mit ganz einfachen Betrachtungen beginnen. Nach der Theorie von Broensted sind Säuren Protonendonatoren und Basen Protonenakzeptoren. Das Bestreben einer Säure ein Proton abzugeben und das Bestreben einer Base ein Proton aufzunehmen bestimmt die Stärke einer Säure bzw. Base.
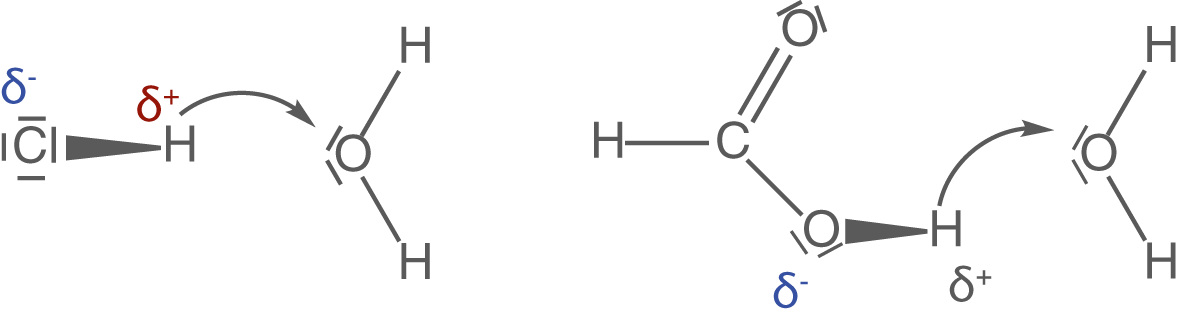
Ein Beispiel zu unterschiedlich starken Säuren liefern die folgenden Protonenübertragungsreaktionen:

Diagramm mit unterschiedlichen grafischen Darstellungen, die sich auf Linien und Formen konzentrieren.
Abb. 1: Protonierung des Wassers

Links siehst du Salzsäure, eine sehr starke und aggressive Säure, welche in wässriger Lösung nahezu komplett dissoziiert. Rechts siehst du die weitaus schwächere organische Ameisensäure oder auch Methansäure, welche ihr Proton weitaus weniger leicht abgibt.
Es gilt nun dieses Bestreben ein Proton abzugeben irgendwie zu quantifizieren, um somit Aussagen über die Stärke der Säure treffen zu können. Wichtig ist an dieser Stelle, dass dieses Konzept im Allgemeinen auch auf funktionelle Gruppen oder ganze Moleküle angewendet werden kann, welche ein oder mehrere Protonen abgeben können. Es geht also nicht nur um Säuren, wie du sie aus dem Unterricht kennst.
Wir werden an dieser Stelle zunächst wieder die Säuren behandeln, da die Basenstärken im Anschluss ganz analog abgehandelt werden können.

Die Säurenkonstante KS und die Basenkonstanten KB

Die Reaktionen von Säuren und Basen sind Gleichgewichtsreaktionen. Das bedeutet, dass wir das Massenwirkungsgesetz zu Rate ziehen können.
Wir betrachten dazu die folgende Säure-Base-Reaktion einer Säure HAc mit Wasser, wobei letzteres hier als Base fungiert:

\(\text{HAc}_{(\text{aq})}+\text{H}_{2}\text{O}_{(\ell)}\) \(\rightleftharpoons\) \(\text{Ac}_{(\text{aq})}^{-}+\text{H}_{3}\text{O}_{(\text{aq})}^{+}\)

Für diese Reaktion können wir das Massenwirkungsgesetz formulieren:

\(K\) = \(\dfrac{c(\text{Ac}_{(\text{aq})}^{-})\cdot c(\text{H}_{3}\text{O}_{(\text{aq})}^{+})}{c(\text{HAc}_{(\text{aq})})\cdot c(\text{H}_{2}\text{O}_{(\ell)})}\)

Bereits bei der Autoprotolyse des Wassers hatten wir so ein ähnliches MWG, in welchem die Konzentration des Wassers im Nenner vorkam. Wir hatten dort gesagt, dass sich diese Konzentration kaum ändert, da nur ein sehr geringer Anteil an Wasser wirklich protoniert wird. Diese Vereinfachung können wir an dieser Stelle auch wieder verwenden und die Konzentration des Wassers in die Gleichgewichtskonstante ziehen:

\(K\cdot c(\text{H}_{2}\text{O}_{(\ell)})\) = \(K_{\text{S}}\) = \(\dfrac{c(\text{Ac}_{(\text{aq})}^{-})\cdot c(\text{H}_{3}\text{O}_{(\text{aq})}^{+})}{c(\text{HAc}_{(\text{aq})})}\)

Dem Produkt der Gleichgewichtskonstanten \(K\) und der Wasserkonzentration geben wir eine neue Bezeichnung: die Säurekonstante \(K_{\text{S}}\)

Ganz analog dazu können wir auch einen \(K_{\text{B}}\)-Wert definieren, welcher als Basenkonstante bezeichnet wird. Dazu betrachten wir folgendes Gleichgewicht mit der Base B und Wasser, welches jetzt die Rolle der Säure einnimmt.

\(\text{Ac}_{(\text{aq})}^{-}+\text{H}_{2}\text{O}_{(\ell)}\) \(\rightleftharpoons\) \(\text{HAc}_{(\text{aq})}+\text{OH}_{(\text{aq})}^{-}\)

Beim Massenwirkungsgesetz können wir die Wasserkonzentration wieder in die Gleichgewichtskonstante \(K\) ziehen:

\(K\cdot c(\text{H}_{2}\text{O}_{(\ell)})\) = \(K_{\text{B}}\) = \(\dfrac{c(\text{HAc}_{(\text{aq})})\cdot c(\text{OH}_{(\text{aq})}^{-})}{c(\text{Ac}_{(\text{aq})}^{-})}\)

Wir erhalten die Basenkonstante \(K_{\text{B}}\).

Mithilfe dieser beiden speziellen Gleichgewichtskonstanten können wir nun bereits Aussagen über die Stärken von Säuren und Basen treffen:

  • Säuren: je stärker eine Säure ist, desto größer ist die Säurekonstante; für sehr starke Säuren gilt \(K_{\text{S}}>>1\)
  • Basen: je stärker eine Base ist, desto größer ist die Basenkonstante; für sehr starke Basen gilt \(K_{\text{B}}>>1\)
Diesen Umstand können wir uns mit dem Wissen um chemische Gleichgewichte erklären. Je stärker eine Säure ist, desto leichter gibt sie ein Proton ab es bilden sich Oxonium-Ionen aus. Mit der Definition des pH-Werts wissen wir bereits, je mehr Oxonium-Ionen in der Lösung sind, desto geringer ist der pH-Wert und desto saurer ist die Lösung. Liegen viele Oxonium-Ionen vor, dann liegt das Gleichgewicht weit auf der Produktseite und die Säurekonstante wird größer als eins sein.
Ganz analog ist auch die Basenstärke zu erklären: je mehr Hydroxid-Ionen in der Lösung vorkommen, desto weiter liegt das Gleichgewicht auf der Produktseite der betreffenden Gleichgewichtsreaktion.

pKS- und pKB-Werte

Sehr oft wird statt der Säure- bzw. Basenkonstante der negative dekadische Logarithmus dieser Größen angegeben. Im Falle von Säuren wird in diesem Fall der \(\text{pK}_{\text{S}}\)-Wert verwendet und im Falle von Basen der \(\text{pK}_{\text{B}}\)-Wert.

\(\text{pK}_{\text{S}}\) = \(-\lg\left(\dfrac{K_{\text{S}}}{\text{mol}\cdot\ell^{-1}}\right)\)

Formal müssen wir wieder darauf achten, dass im Argument des Logarithmus (in der Klammer) keine Einheit steht, da wir aus Einheiten keinen Logarithmus ziehen können.
Bevor wir den \(\text{pK}_{\text{B}}\)-Wert definieren schauen wir uns in zwei Beispielen an, worin der Unterschied zur eben eingeführten Säurekonstanten besteht:

Beispiel A

\(K_{\text{S}}>>1\)

Beispielhaft wollen wir hier annehmen, dass \(K_{\text{S}}=10\). Nun berechnen wir den \(\text{pK}_{\text{S}}\)-Wert.

\(\text{pK}_{\text{S}}\) = \(-\lg(K_{\text{S}})\) = \(-\lg(10)\) = \(-1\)

Beispiel B

\(K_{\text{S}}<<1\)

Beispielhaft wollen wir hier annehmen, dass \(K_{\text{S}}=0,1=1\cdot10^{-1}\). Nun berechnen wir den \(\text{pK}_{\text{S}}\)-Wert.

\(\text{pK}_{\text{S}}\) = \(-\lg(K_{\text{S}})\) = \(-\lg(0,1)\) = \(-\lg(1\cdot10^{-1})\) = \(1\)
Merke:
Je stärker die Säure, desto größer die Säurekonstante \(K_\text{S}\) und desto kleiner der \(\text{pK}_{\text{S}}\)-Wert
Die Definition des \(\text{pK}_{\text{B}}\)-Werts folgt analog dem \(\text{pK}_{\text{S}}\)-Wert:

\(\text{pK}_{\text{B}}\) = \(-\lg\left(\dfrac{K_{\text{B}}}{\text{mol}\cdot\ell^{-1}}\right)\)

Durch Umformen der Gleichungen kannst du bei gegebenem \(\text{pK}_{\text{S}}\)-Wert bzw. \(\text{pK}_{\text{B}}\)-Wert natürlich auch die zugehörige Säure- bzw. Basekonstante berechnen.

\(K_{\text{S}}\) = \(10^{(-\text{pK}_{\text{S}})}\;\text{mol}\cdot\ell^{-1}\)
\(K_{\text{B}}\) = \(10^{(-\text{pK}_{\text{B}})}\;\text{mol}\cdot\ell^{-1}\)

Zum Abschluss wollen wir uns nun noch den Zusammenhang zwischen \(\text{pK}_{\text{S}}\)- und \(\text{pK}_{\text{B}}\)-Wert anschauen. Dafür nehmen wir die äure- und Basenkonstante zur Hilfe:

\(K_{\text{S}}\cdot K_{\text{B}}\)= \(c(\text{H}_{3}\text{O}_{(\text{aq})}^{+})\cdot c(\text{OH}_{(\text{aq})}^{-})\)

Durch Kürzen von \(c(\text{Ac}_{(\text{aq})}^{-})\) und \(c(\text{HAc}_{(\text{aq})})\) erhalten wir die Gleichung, die wir bereits als das Ionenprodukt des Wassers kennen:

\(K_{\text{S}}\cdot K_{\text{B}}\) = \((\text{H}_{3}\text{O}_{(\text{aq})}^{+})\cdot c(\text{OH}_{(\text{aq})}^{-})\) = \(K_{\text{W}}\) = \(10^{-14}\,\text{mol}^{2}\cdot \ell^{-2}\)

Nun wenden wir den negativen dekadischen Logarithmus auf diese Gleichung an:

\(\text{pK}_{\text{S}}+\text{pK}_{\text{B}}=\text{pK}_{\text{W}}\) = \(14\)

Wichtig:
Denke daran, dass sowohl der \(\text{pK}_{\text{S}}\)-Wert als auch der \(\text{pK}_{\text{B}}\)-Wert kleiner als 0 oder größer als 14 sein können. Nur die Summe der beiden Werte ist gleich 14.

Jede Säure hat demnach ihren zugehörigen \(\text{pK}_{\text{S}}\)-Wert und die korrespondierende Base ihren \(\text{pK}_{\text{B}}\)-Wert. Weiterhin wird hieran auch deutlich, dass sehr starke Säuren sehr schwache korrespondierende Basen haben und umgekehrt. Dies folgt daraus, dass diese beiden Werte in der Summe 14 ergeben müssen.

Bildnachweise [nach oben]
[1]
© 2016 - SchulLV.