Primärelemente

Das Leclanché-Element

Im Zusammenhang mit der Elektrochemie lernst du die theoretischen Grundlagen in Form von Redox-Reaktionen, dem Standardpotential und der elektrochemischen Spannungsreihe kennen. Die ersten Anwendungen umfassen die Begriffe des Galvanischen Elements und der Elektrolyse. Wir wollen uns nun konkreten Anwendungen zuwenden, die uns in Form alltäglicher Anwendungen bekannt sind. Dieses Skript greift auf alle Inhalte der Elektrochemie zurück, die du im Rahmen der Oberstufe kennen gelernt hast.

Als erstes wollen wir uns mit Batterien beschäftigen, die auch unter dem Begriff des Primärelements bekannt sind. Batterien sind ein wichtiger Bestandteil vieler Elektrogeräte und wir werden lernen, wie die elektrische Energie in Form von chemischer Energie gespeichert werden kann und warum Batterien nicht wieder aufladbar sind.

Galvanische Elemente, bei welchen die Redox-Reaktion nicht mehr umkehrbar ist, werden Primärelemente oder auch Batterien genannt.

Wir wollen uns beispielhaft das Leclanché-Element anschauen. Dieses wurde bereits 1866 vom französischen Chemiker Georges Leclanché patentiert.

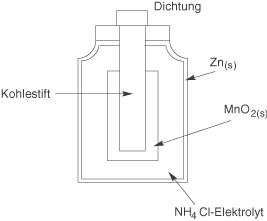
Unten siehst du den Aufbau eines Leclanché-Elements. Die Anode liegt in Form des elementaren Zinks vor, welches die Ummantelung bildet. Das Innenleben baut sich von Außen nach Innen wie folgt auf: Auf die Zinkummantellung folgt das Elektrolyt in Form einer eingedickten Ammoniumchlorid-Lösung $\text{NH}_{4}\text{Cl}$ . Hierzu wird beispielsweise Stärke verwendet und stellt einen Schutz gegen das Auslaufen dar. In der Mitte des Leclanché-Elements befindet sich ein Kohlestift, welcher mit Braunstein (Mangandioxid $\text{MnO}_{2}$ ) ummantelt ist. Eine Dichtung sorgt dafür, dass nichts aus der Batterie austreten kann. Wir wollen uns nun anschauen, welche Redox-Reaktionen hier ablaufen.

Abb. 1: Aufbau eines Leclanché-Elements

Wir unterteilen die Gesamtreaktion zur besseren Übersichtlichkeit in Anodenreaktion, Kathodenreaktion und die Reaktion des Elektrolyten.

Anodische Oxidation

An der Anode läuft immer die Oxidation ab. In diesem Fall wird elementares Zink zu $\text{Zn}^{2+}$ oxidiert und stellt zwei Elektronen für die Reduktion bereit.

$\text{Zn}$ $\longrightarrow$ $\text{Zn}^{2+}+2\,\text{e}^{-}$

Kathodische Reduktion

Die Reduktion fällt in diesem Fall etwas komplizierter aus. Dazu betrachten wir zunächst die Oxidationszahl von Mangan in Braunstein. Sauerstoff hat in Verbindungen fast immer die Oxidationszahl -II (Ausnahme Peroxide). Bei zwei Sauerstoffatomen erhalten wir so -IV. Da Braunstein nach außen hin neutral sein muss, müssen diese vier negativen Ladungen von vier positiven kompensiert werden: Mangan in $\text{MnO}_{2}$ hat die Oxidationzahl +IV. Die Reduktion sieht folgendermaßen aus.

$2\,\text{MnO}_{2}+2\,\text{H}^{+}+2\,\text{e}^{-}$ $\longrightarrow$ $2\,\text{MnO(OH)}$

Wir wollen nun auch die Oxidationszahl von Mangan in dem gebildeten Produkt bestimmt. Dieses ist als Manganit oder auch Manganoxidhydroxid bekannt. In der Summe besitzen die beiden Sauerstoffatome eine negative Ladung von -IV. Das Wasserstoffatom hat eine Ladung von +I, folglich bleibt ein Rest von -III übrig, welcher durch Mangan kompensiert werden muss: Mangan besitzt hier die Ladung +III, wurde also reduziert.

Elektrolyt-Reaktion

Durch die Freisetzung von $\text{Zn}^{2+}$ -Kationen während der Redox-Reaktion kommt es zu deren Reaktion mit dem Elektrolyten. Hierbei kommt es nach der Deprotonierung von Ammonium-Kationen zur Ausbildung einer Komplexverbindung.

$\text{Zn}^{2+}+2\,\text{NH}_{4}\text{Cl}$ $\longrightarrow$ $[\text{Zn(NH)_{3}}_{2}]\text{Cl}_{2}+2\,\text{H}^{+}$

Gesamtreaktion

Durch die Kombination dieser drei Teilreaktionen erhalten wir die Gesamtreaktion:

$\text{Zn}+2\,\text{MnO}_{2}+2\,\text{NH}_{4}\text{Cl}$ $\longrightarrow$ $[\text{Zn(NH)_{3}}_{2}]\text{Cl}_{2}+2\,\text{MnO(OH)}$

Diese liefert eine nutzbare elektromotorische Kraft von ca. $1,5\,\text{V}$ , welche in diesem Zusammenhang auch als Nennspannung bezeichnet wird.

Energiereichere Primärelemente - Ein Überblick

Das Leclanché-Element ist bereits seit über 150 Jahren bekannt, dementsprechend gibt es bereits leistungsfähigere Primärelemente, über die wir uns hier einen Überblick verschaffen wollen.

Eine leistungsstärkere Batterie liegt in Form der Alkali-Mangan-Batterie vor. Deren Nennspannung beträgt ebenfalls $1,5\,\text{V}$ . An der Anode wird wie im Fall des Leclanché-Elements Zink zu $\text{Zn}^{2+}$ oxidiert. Unterschiede liegen im Fall der Kathodenreaktion und des Elektrolyten vor. Letzterer stellt in diesem Fall Kalilauge ( $\text{KOH}_{(\text{aq})}$ ) dar. An der Anode wird Braunstein ( $\text{MnO}_{2}$ ) in zwei Schritten reduziert. Zunächst erfolgt die Reduktion von Mangan(IV) unter Bildung von Manganit zu Mangan(III):

$\text{MnO}_{2}+\text{H}_{2}\text{O}+2\text{e}^{-}$ $\longrightarrow$ $\text{MnO(OH)}+\text{OH}^{-}$

Anschließend wird Mangan(III) unter Bildung von Mangan(II)hydroxid zu Mangan(II) reduziert.

$\text{MnO(OH)}+\text{H}_{2}\text{O}+2\text{e}^{-}$ $\longrightarrow$ $\text{Mn(OH)}_{2}+\text{OH}^{-}$

Die Gesamtreaktion können wir so schreiben:

$\text{Zn}+\text{MnO}_{2}+2\,\text{H}_{2}\text{O}$ $\longrightarrow$ $\text{Mn(OH)}_{2}+\text{Zn}^{2}+2\,\text{OH}^{-}$

Lithium-Batterien

Lithium-Batterien stellen sehr leistungsfähige Primärelemente dar. Das liegt einerseits an dem relativ negativen Redoxpotential des Redox-Paares $\text{Li}/\text{Li}^{+}$ mit $E^{0}(\text{Li}/\text{Li}^{+})=-3,04\,\text{V}$ , was zu hohen Nennspannungen führt. Des Weiteren ist Lithium das leichteste aller Metalle, da es an dritter Stelle im Periodensystem der Elemente zu finden ist. Das führt zu einer zusätzlichen Gewichtsersparnis. Durch die sehr hohe Energiedichte von Lithium-Batterien, können hier relativ kleine Bauteile verwirklicht werden, die insbesondere im 21. Jahrhundert vielfältige Anwendungsfelder besitzen. Ein Beispiel für eine Lithium-Batterie stellt das Lithium-Schwefeldioxid-System dar.
Hier läuft vereinfacht folgende Redox-Reaktion ab:

$2\,\text{Li}+2\,\text{SO}_{2}$ $\longrightarrow$ $\text{Li}_{2}\text{S}_{2}\text{O}_{4}$

Hier wird Lithium zu $\text{Li}^{+}$ oxidiert und der Schwefel wird von $\text{S}^{4+}$ zu $\text{S}^{3+}$ reduziert. Die hier erreichte Nennspannung liegt bei $2,9\,\text{V}$ . Bei der Verwendung von Thionylchlorid ( $\text{SOCl}_{2}$ ) statt Schwefeldioxid werden sogar Nennspannungen von $3,65\,\text{V}$ realisiert. Im Falle dieses Lithium-Thionylchlorid-Systems kann folgende Redox-Reaktion formuliert werden:

$2\,\text{Li}+2\,\text{SOCl}_{2}$ $\longrightarrow$ $4\,\text{LiCl}+\text{SO}_{2}+\text{S}$

Hierbei kommt es zur Bildung von Schwefeldioxid und elementarem Schwefel. Wichtig ist in allen Fällen, dass Lithium-Batterien, egal welcher Zusammensetzung, sehr energiereiche und gleichzeitig hochgiftige Verbindungen enthalten. Ein Auslaufen der Elemente ist also in jedem Fall zu vermeiden.

Brennstoffzellen - Die „Knallgaszelle“

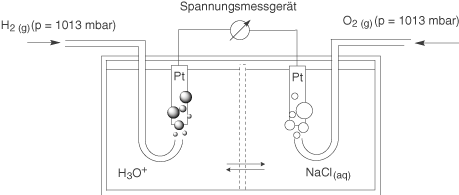
Brennstoffzellen unterscheiden sich von Primär- und Sekundärelementen (Sekundärelemente besprechen wir im nächsten Kapitel) in der Form, dass die Edukte nicht in der Zelle vorliegen, sondern von außen zugeführt werden müssen. Während Primär- und Sekundärelemente Energiespeicher darstellen, können Brennstoffzellen als Energiewandler bezeichnet werden. Die „Knallgaszelle“ ist eine Brennstoffzelle, welche in einer kontrollierten Knallgasreaktion Energie aus der Reaktion von elementarem Wasserstoff und Sauerstoff gewinnt. Wir betrachten zunächst den Aufbau der Zelle:

Abb. 2: Aufbau einer Brennstoffzelle

Hierbei handelt es sich um ein Galvanisches Element, welches mithilfe der Redox-Paare $\text{H}_{2}/2\,\text{H}^{+}$ und $2\,\text{O}^{2-}/\text{O}_{2}$ betrieben wird. Die Edukte werden gasförmig bei konstantem Druck auf eine platinierte Platinelektrode geleitet, an welcher die Teilreaktionen stattfinden. Diese können wir folgendermaßen aufteilen:

Oxidation

$\text{H}_{2}$ $\longrightarrow$ $2\,\text{H}^{+}+2\,\text{e}^{-}$

Diese Reaktion entspricht derjenigen, die auch in der Standardwasserstoffhalbzelle abläuft und deren Redox-Potential für die elektrochemische Spannungsreihe als Nullpunkt gewählt wird.

Reduktion

$\text{O}_{2}+4\,\text{e}^{-}$ $\longrightarrow$ $2\,\text{O}^{2-}$

Hier wird Sauerstoff reduziert. Wir werden nun die beiden Teilgleichungen zur Redox-Reaktion zusammenfassen:

Redox-Reaktion

$\text{O}_{2}+2\,\text{H}_{2}$ $\longrightarrow$ $2\,\text{H}_{2}\text{O}$

Was du hier sehen kannst, ist, dass das Produkt dieser Reaktion gewöhnliches Wasser ist. Für diese Brennstoffzellen werden Nennspannungen um $1\,\text{V}$ erreicht.
Im Zusammenhang mit der $\text{CO}_{2}$ -Problematik und dem damit verbundenen anthropogenen Klimawandel werden solche alternativen Energiequellen immer wichtiger. Die Produkte sind hierbei in keinem Fall umweltschädlich und tragen somit nicht zu einer Klimaänderung bei. Die Brennstoffzelle kann sinnbildlich für eine breite Palette an Energiequellen gesehen werden, die eine emissionsarme bis sogar emissionsfreie Energieproduktion ermöglichen würde. Diese Sparte ist insbesondere heute Bestandteil der Forschung, um auf diesem Weg Alternativen für die Verwendung von bspw. Rohöl zu finden.

Sekundärelemente - Der Bleiakkumulator

Im Falle der Primärelemente haben wir Reaktionen vorliegen, die sich nicht umkehren lassen: Ein Aufladen, in dem Sinn, dass elektrische Energie wieder in Form von chemischer gespeichert wird, kann hier nicht bewerkstelligt werden. Im Gegenteil hierzu stehen Sekundärelemente, welche auch unter dem Begriff der Akkumulatoren („Akkus“) bekannt sind. Der Unterschied liegt hier darin begründet, dass die Redox-Reaktion, die während des Entladevorgangs abläuft, durch das Anlegen einer äußeren Spannung umkehrbar ist (Prinzip der Elektrolyse).

Galvanische Elemente, bei welchen die Redox-Reaktion umkehrbar ist, die folglich wieder „aufgeladen“ werden können, werden Sekundärelemente oder auch Akkumulatoren genannt.

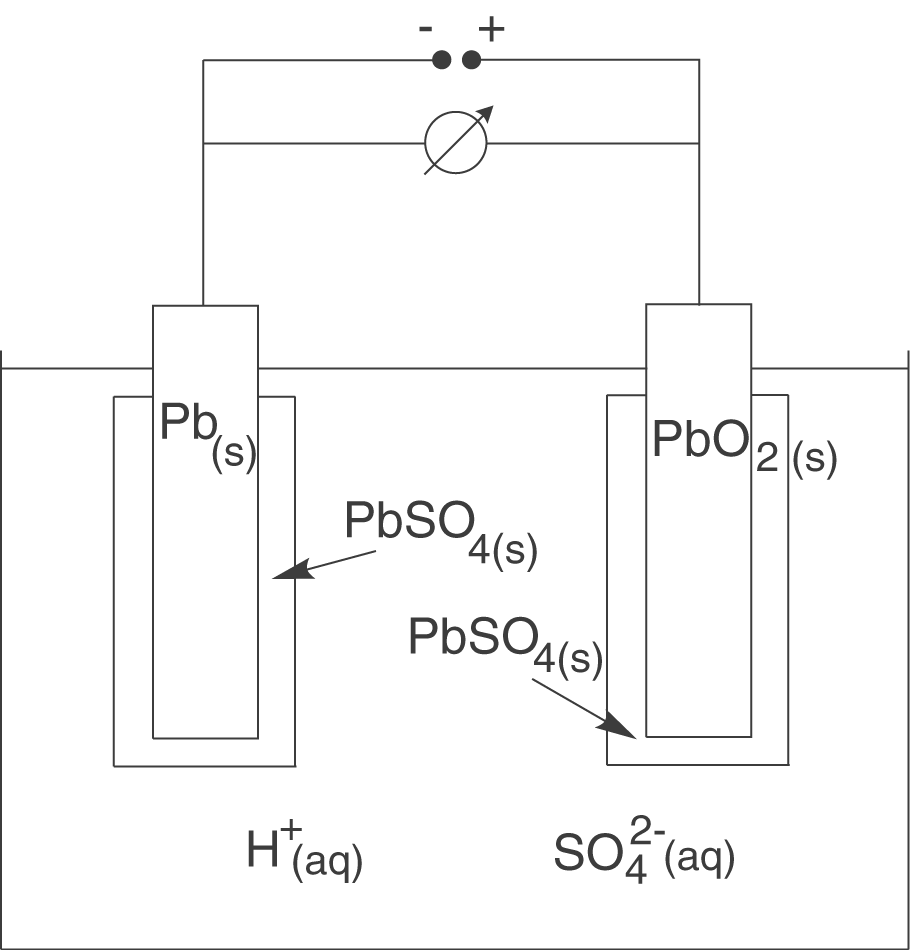
Wir wollen uns hier einen der bekanntesten Akkumulatoren genauer anschauen: den Bleiakkumulator. Der Aufbau gestaltet sich grob gesehen folgendermaßen:

Abb. 3: Aufbau eines Bleiakkus

Blei liegt in diesem Fall in drei unterschiedlichen Oxidationsstufen vor: Wlementares Blei ( $\text{Pb}^{0}$ ), Blei(II) ( $\text{Pb}^{2+}$ ) in Bleisulfat ( $\text{PbSO}_{4}$ ) sowie Blei(IV) in Bleidioxid ( $\text{PbO}_{2}$ ). Durch die unterschiedlichen Oxidationstufen erhalten wir hier zwei verschieden Redox-Paare $\text{Pb/PbSO}_{4}$ und $\text{PbSO}_{4}/\text{PbO}_{2}$ . Es laufen folgende Teilreaktionen ab:

Anodische Oxidation

An der Anode wird elementares Blei zu Blei(II) oxidiert.

$\text{Pb}+\text{SO}_{4}^{2-}$ $\longrightarrow$ $\text{PbSO}_{4}+2\,\text{e}^{-}$

Hierbei ist wichtig, dass wir das Sulfat-Anion nicht vernachlässigen. Das Redox-Paar $\text{Pb/PbSO}_{4}$ weist nämlich ein niedriger Standardpotential auf, als das Redox-Paar $\text{Pb/Pb}^{2+}$ .

Anmerkung: Wir wollen diesen Unterschied hier etwas ausführlicher betrachten und du wirst lernen, worin dieser begründet liegt. Im diesem Zusammenhang wirst du das Löslichkeitsprodukt und die Nernst-Gleichung kennen lernen. Diese Inhalte sind nicht zwangsweise Schulstoff, für das Verständnis des Unterschieds aber hilfreich.

Wir betrachten zunächst das Lösungsgleichgewicht zwischen Bleisulfat und den beiden beteiligten Ionen in wässriger Lösung.

$\text{PbSO}_{4\,(\text{s})}$ $\rightleftharpoons$ $\text{Pb}_{(\text{aq})}^{2+}+\text{SO}_{4\,(\text{aq})}^{2-}$

Für diese Gleichgewichtsreaktion können wir das Massenwirkungsgesetz formulieren:

$K$ = $\dfrac{c(\text{Pb}_{(\text{aq})}^{2+})\cdot c(\text{SO}_{4\,(\text{aq})}^{2-})}{c(\text{PbSO}_{4\,(\text{s})})}$

Für das Massenwirkungsgesetz gilt, dass die Konzentration von Feststoffen konventionell gleich eins gesetzt wird. Dementsprechend vereinfacht sich das MWG zu:

$K_{\text{L}}$ = $c(\text{Pb}_{(\text{aq})}^{2+})\cdot c(\text{SO}_{4\,(\text{aq})}^{2-})$

Diese Form wird Löslichkeitsprodukt genannt, wobei $\boldsymbol{K_{\text{L}}}$ die Löslichkeitskonstante darstellt. Je kleiner $K_{\text{L}}$ , desto schlechter löst sich der betrachtete Stoff in Wasser: Das Gleichgewicht liegt dann weit auf der linken Seite der oben dargestellten Reaktionsgleichung.
Wir gehen nun zur Nernst-Gleichung über. Diese beschreibt die Konzentrationsabhängigkeit des Redoxpotentials. Für das Redox-Paar $\text{Pb}/\text{Pb}^{2+}$ lautet sie:

$E_{\text{h}}$ = $E^{0}+\dfrac{0,059\,\text{V}}{2}\cdot\log\left(\dfrac{c(\text{Pb}_{(\text{aq})}^{2+})}{c(\text{Pb}_{(\text{s})})}\right)$

Die Konzentration von elementarem Blei wird wieder gleich eins gesetzt, da es sich hier um einen Feststoff handelt. Wir verwenden nun das Lösungslichkeitsprodukt von Blei(II)-sulfat, formen dieses nach $c(\text{Pb}_{(\text{aq})}^{2+})$ um und setzen den neuen Ausdruck in die Nernst-Gleichung ein:

$E_{\text{h}}$ = $E^{0}+\dfrac{0,059\,\text{V}}{2}\cdot\log(c(\text{Pb}_{(\text{aq})}^{2+}))\;$ $\text{mit}\;$ $c(\text{Pb}_{(\text{aq})}^{2+})$ = $\dfrac{K_{\text{L}}}{c(\text{SO}_{4\,(\text{aq})}^{2-})}$

$E_{\text{h}}$ = $E^{0}+\dfrac{0,059\,\text{V}}{2}\cdot\log\left(\dfrac{K_{\text{L}}}{c(\text{SO}_{4\,(\text{aq})}^{2-})}\right)$

Der wichtige Aspekt bezieht sich auf den zweiten Term der Formel: Hier taucht die Konzentration von Sulfat auf. Hieran können wir sehen, dass das Redoxpotential unseres Redox-Paares von der Anwesenheit von Sulfat abhängt. Dementsprechend verwenden wir auch das Standardpotential von $\text{Pb}/\text{PbSO}_{4}$ .

Kathodische Reduktion

Nun zurück zum Bleiakkumulator. Nach der anodischen Oxidation folgt die kathodische Reduktion: Hier wird vierwertiges Blei in Bleidioxid zu zweiwertigem Blei in Blei(II)-sulfat reduziert.

$\text{PbO}_{2}+2\,\text{e}^{-}+\text{SO}_{4}^{2-}+4\,\text{H}_{3}\text{O}^{+}$ $\longrightarrow$ $\text{PbSO}_{4}+6\,\text{H}_{2}\text{O}$

Du kannst sehen, dass Oxonium-Kationen für einen Ladungsausgleich sorgen.

Redox-Reaktion

$\text{Pb}+\text{PbO}_{2}+2\,\text{SO}_{4}^{2-}+4\,\text{H}_{3}\text{O}^{+}$ $\rightleftarrows$ $2\,\text{PbSO}_{4}+6\,\text{H}_{2}\text{O}$

Den Gleichgewichtspfeil haben wir hier mit Absicht gewählt. Von links nach rechts läuft die freiwillig Redox-Reaktion während des Entladevorgangs ab. Wenn wir nun eine Gleichspannungsquelle von außen anschließen, dann können wir diese Reaktion umkehren, sodass sie von rechts nach links abläuft. Dies entspricht dem Ladevorgang des Akkumulators. Die prominenteste Verwendung von Bleiakkumulatoren ist in Form von Autobatterien.

Bildnachweise [nach oben]

[1]

[2]

[3]