Reaktionsgeschwindigkeit

Einführung

Nachdem du in den vorherigen Kapiteln die Grundlagen des chemischen Gleichgewichts kennen gelernt hast und wir diskutiert haben, wie ein chemisches Gleichgewicht beeinflusst wird, wollen wir an dieser Stelle den Begriff der Reaktionsgeschwindigkeit näher betrachten.
Wir wollen klären, was die Reaktionsgeschwindigkeit ist, auf ihre Formulierung eingehen und abschließend dazu übergehen ihre entscheidende Rolle im Falle des chemischen Gleichgewichts zu erörtern.

Wichtig:

Du wirst an dieser Stelle sicher ein paar neue Informationen bekommen und einige Formulierungen sehen, die du so im Unterricht noch nicht gesehen hast. Zum Verständnis des Begriffs der Reaktionsgeschwindigkeit ist das hilfreich, du benötigst dieses Wissen jedoch nicht konkret für deine Abiturprüfung in Chemie. Dazu genügt es zu wissen, was die Reaktionsgeschwindigkeit ist und in welchem Zusammenhang sie zum chemischen Gleichgewicht steht.

Grundlagen der Reaktions-geschwindigkeit: das Kollisionsmodell

Gegeben sei eine Reaktion

$\text{A}+\text{B}$ $\rightleftharpoons$ $\text{C}$

Der Begriff des Kollisionsmodells beschreibt seinen Inhalt bereits treffend: es geht um Teilchen, die miteinander kollidieren und dabei reagieren. Teilchen sind hier die Reaktanden (Atome oder Moleküle) dieser Reaktion. Die Teilchen fliegen im Vakuum umher:

Abb. 1: Stoßmodell

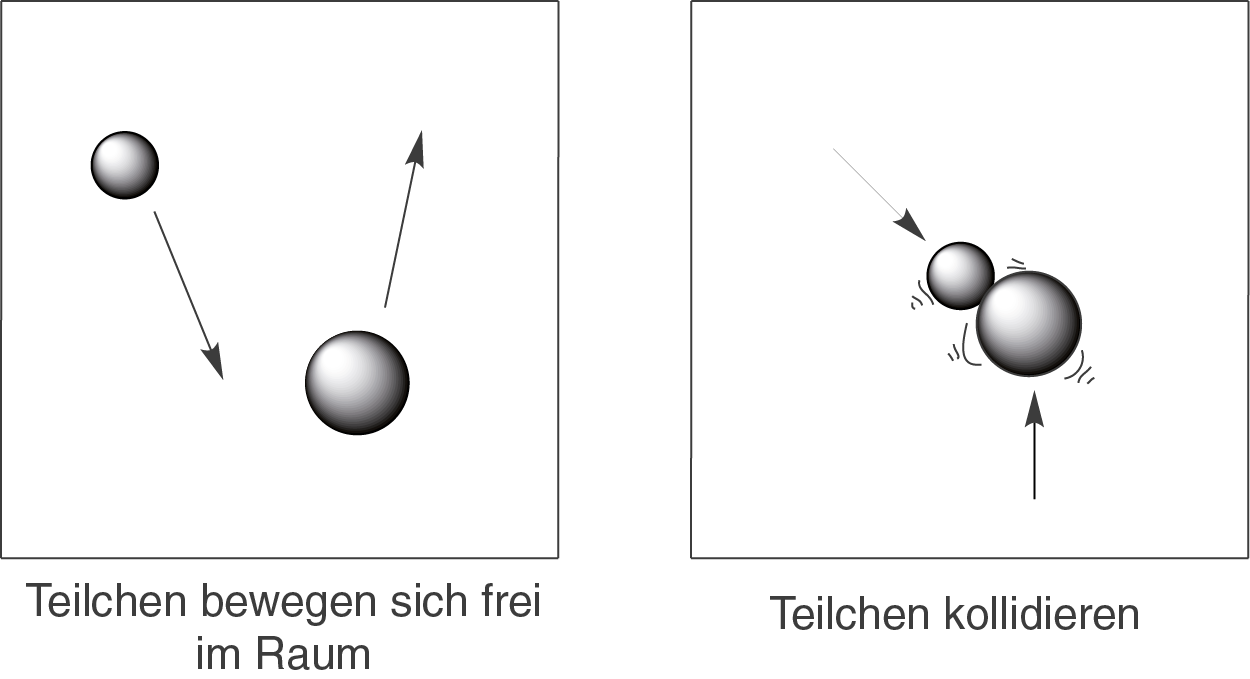
Zu einer chemischen Reaktion kann es immer dann kommen, wenn die beiden kollidieren (s. rechtes Schaubild).

Wichtig:

Das Kollisionsmodell kann sehr schnell sehr kompliziert werden, wenn davon ausgegangen wird, dass nicht jede Kollision auch zur Bildung eines Produkts führt. Gründe hierfür sind beispielsweise das Erreichen der für die Reaktion notwendigen Aktivierungsenergie oder die räumliche Ausrichtung der Teilchen zueinander, wenn der Angriff (z.B. durch sterische Hinderung) nur aus einer bestimmten Richtung zum Erfolg führen kann. Werden diese und weitere Aspekte beachtet, nimmt die Komplexität deutlich zu und man gelangt zur sog. Stoßtheorie. Wir werden uns aber nur auf ein paar wichtige Effekt konzentrieren.

Die Geschwindigkeit einer Reaktion hängt immer von der Zahl der erfolgreichen Zusammenstöße ab. Je mehr solcher Kollisionen es gibt, desto schneller läuft die Reaktion ab.
Bevor wir uns nun der mathematischen Beschreibung der Reaktionsgeschwindigkeit zuwenden, wollen wir noch einen kurzen Blick auf die Temperatur- und Druckabhängigkeit im Kollisionsmodell werfen.

Temperaturerhöhung im Kollisionsmodell

Um den Effekt einer Temperaturerhöhung auf die beiden Reaktanden in unserem geschlossenen System verstehen zu können, wollen wir uns kurz überlegen, was mit diesen beiden dabei geschieht.
Die Temperaturerhöhung eines Systems entspricht einer Erhöhung der Energie der darin befindlichen Teilchen. Wenn wir die Temperatur erhöhen, indem wir von außen dem System Wärmeenergie zuführen, hat das zur Folge, dass die kinetische Energie der Teilchen steigt. Eine Temperaturerhöhung hat also den Effekte, dass sich die Teilchen schneller bewegen.
Zwar steigt die Anzahl der Kollisionen dabei nur minimal, jedoch wird durch die höhere Bewegungsenergie die Aktivierungsenergie, die für das Zustandekommen einer Reaktion überwunden werden muss, leichter erreicht.

Druckerhöhung im Kollisionsmodell

Den Effekt einer Druckerhöhung kannst du dir gut graphisch veranschaulichen. Dazu denken wir uns einfach, dass unser System durch einen äußeren Druck verformbar wäre. Wir können das Volumen demnach verringern, wie bei einem Ballon den wir zusammendrücken.

Abb. 2: Druckerhöhung

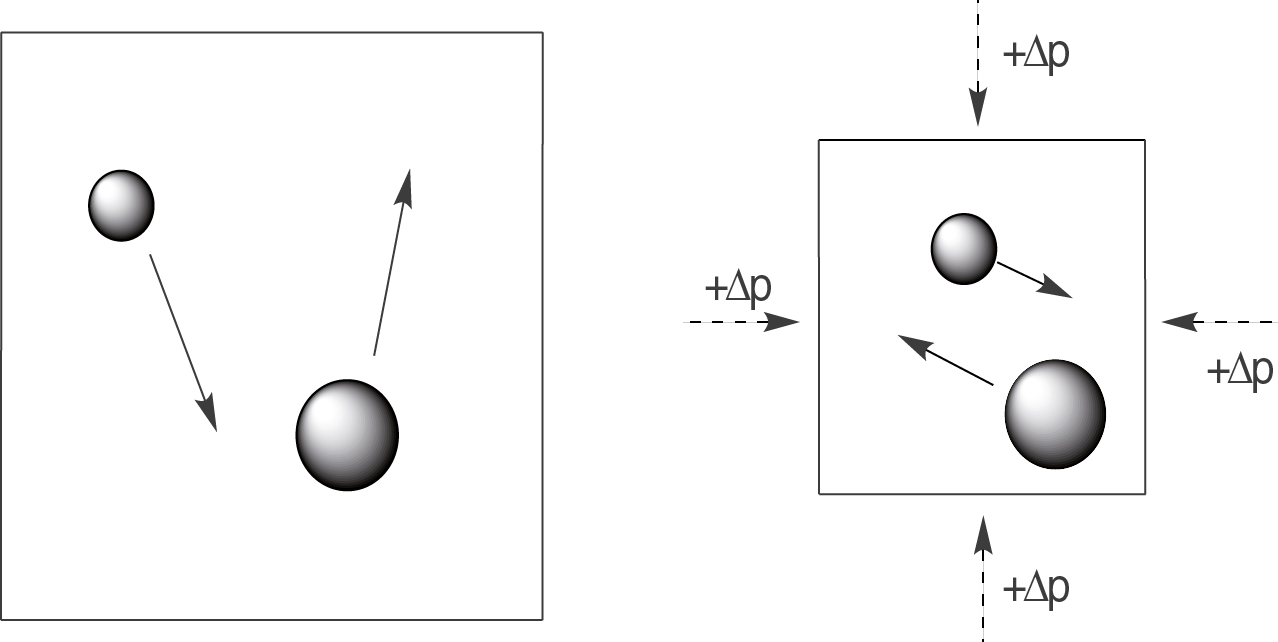
Wie du sehen kannst, verkleinert der äußere Druck das Volumen des Systems, in dem sich die Teilchen aufhalten. Für diese bedeutet das, dass sie sich öfters treffen werden. Häufigere Kollisionen erhöhen die Wahrscheinlichkeit, dass eine Reaktion stattfindet.

Die Reaktions-geschwindigkeit $v$ _Reaktion

Die Reaktionsgeschwindigkeit $v_{\text{Reaktion}}$ beschreibt die zeitliche Änderung der Konzentration eines Reaktanden innerhalb einer Reaktion

In Kapitel drei haben wir die Reaktionsgeschwindigkeit $v_{\text{Reaktion}}$ bereits im Rahmen der Herleitung des Massenwirkungsgesetzes kennen gelernt. Diesen Zusammenhang wollen wir an dieser Stelle aufgreifen und näher betrachten, um verstehen zu können, welche Informationen sich hinter der Größe der Reaktionsgeschwindigkeit verbirgt. Wir betrachten eine allgemeine Reaktion:

$\text{A}+\text{B}$ $\longrightarrow$ $\text{C}$

Dabei kennen wir die folgenden Größen zu der Reaktion:

$c_{\text{A}}$ : Stoffmengenkonzentration des Reaktanden A
$c_{\text{B}}$ : Stoffmengenkonzentration des Reaktanden B
$k$ : Geschwindigkeitskonstante der Reaktion

Für diese Reaktion ergibt sich dann mit den gegebenen Größen das folgende Geschwindigkeitsgesetz:

$v_{\text{Reaktion}}$ = $k\cdot c_{\text{A}}\cdot c_{\text{B}}$

In der oben aufgeführten Reaktion nimmt die Konzentration der Edukte über die Zeit gesehen ab, während sich das Produkt bildet. Diese Abnahme kann sich von Reaktion zu Reaktion stark unterscheiden und beispielsweise sehr langsam oder in einem anderen Fall sehr schnell sein. Die Änderung (Abnahme oder Zunahme) der Konzentration eines Reaktanden pro Zeiteinheit wird aus diesem Grund als Reaktionsgeschwindigkeit bezeichnet.
Grundsätzlich verhält sich diese Reaktionsgeschwindigkeit so, dass sie von Betrag her zu Beginn der Reaktion sehr groß ist und bis zum Erreichen des Gleichgewichtszustands einen konstanten Wert annimmt. Wir wollen uns dieses Verhalten aus diesem Grund in drei unterschiedlichen Zeitintervallen an folgender Graphik anschauen:

Abb. 3: Unterteilung in Zeitintervalle zur Bestimmung der Reaktionsgeschwindigkeit

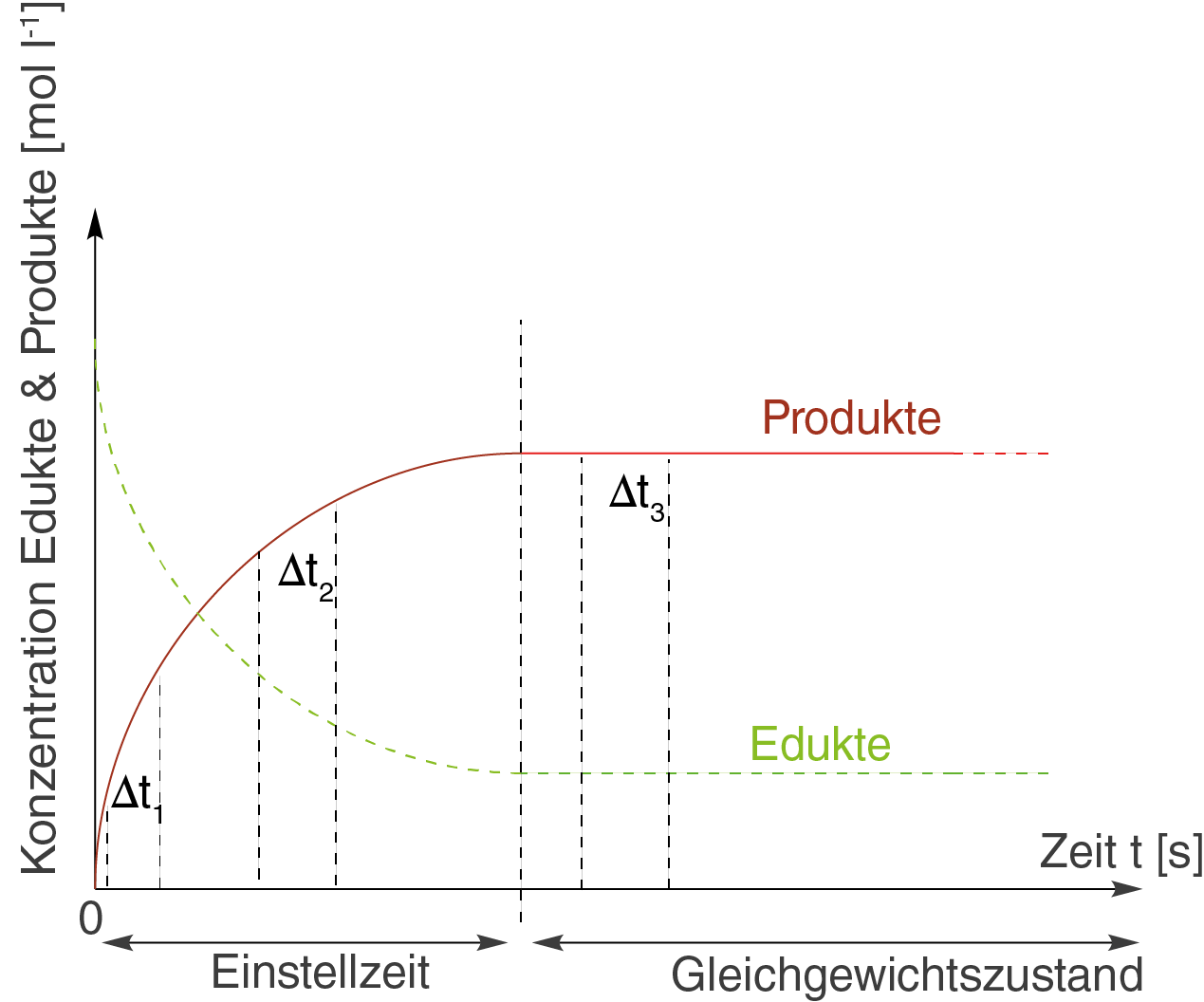
Die drei Zeitintervalle sind dabei mit $\Delta t_{1}$ , $\Delta t_{2}$ und $\Delta t_{3}$ bezeichnet. Bevor wir das ganze rechnerisch angehen, kannst du dir zunächst einmal die beiden Kurven genauer anschauen. Du kannst sehen, dass beide am Anfang sehr steil verlaufen und mit größerem $t$ , also zunehmender Zeit, abflachen. Diese anfänglich steilen Kurvenverläufe weißen auf hohe Reaktionsgeschwindigkeiten hin, da sich die Konzentration in kurzer Zeit stark ändert.
Um die Konzentrationsänderung in diesen Zeitintervallen zu beschreiben, verwenden wir ein Steigungsdreieck. Dieses liefert uns eine mittlere Reaktionsgeschwindigkeit als Konzentrationsänderung $\Delta c$ im Zeitinterval $\Delta t$ .

$v_{\text{Mittel}}$ = $\dfrac{\Delta c}{\Delta t}$

Für die drei zufällig gewählten Zeitintervalle in der oberen Graphik, erhalten wir an dieser Stelle aufgrund unterschiedlicher Konzentrationsänderungen unterschiedliche mittlere Reaktionsgeschwindigkeiten.
In der nächsten Graphik siehst du ein beispielhaftes Steigungsdreieck:

Abb. 4: Anlegung eines Steigungsdreiecks

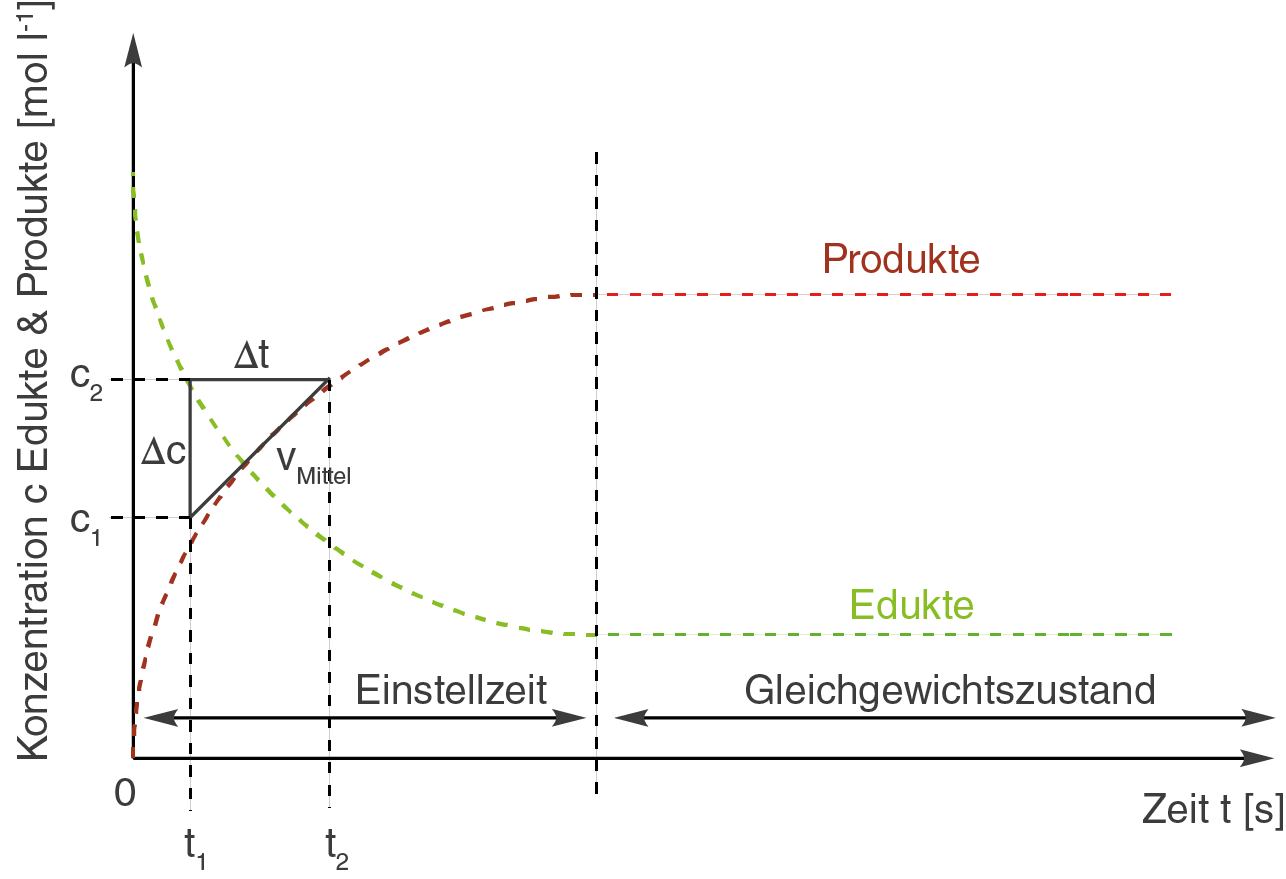
Bei der Konzentrationsänderung $\Delta c$ und der Zeitänderung $\Delta t$ handelt es sich um die Differenz zweier Größen:

$\dfrac{c_{2}-c_{1}}{t_{2}-t_{1}}$ = $\dfrac{\Delta c}{\Delta t}$ = $v_{\text{Mittel}}$

Mit diesem Vorgehen haben wir jedoch nur eine mittlere Reaktionsgeschwindigkeit für das Zeitintervall $\Delta t$ berechnen können. Das Problem ist dabei, dass sich die Reaktionsgeschwindigkeit bereits über einen sehr viel kürzeren Zeitraum ändert.
Das kannst du an der folgenden Graphik sehen:

Abb. 5: Konzentrationsverläufe

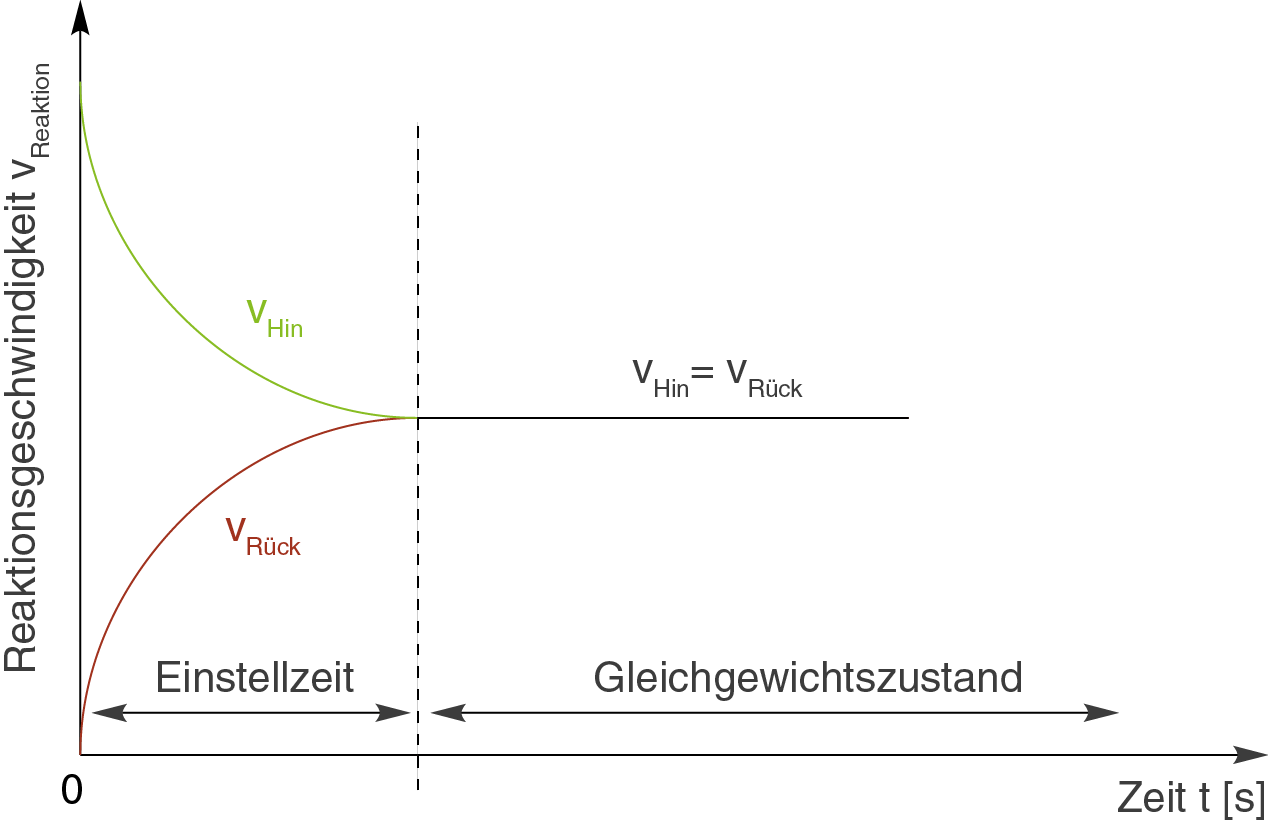
Die beiden Kurven sind die Graphen einer Funktion, die die Geschwindigkeit in Abhängigkeit von der Zeit beschreibt. Du kannst sehen, dass die Reaktionsgeschwindigkeit der Hin- und Rückreaktion im Gleichgewicht einen konstanten Wert annimmt.
Wir wollen nun beispielhaft schauen, wo der große Unterschied zwischen der mittleren Reaktionsgeschwindigkeit $v_{\text{Mittel}}$ und der momentanen Reaktionsgeschwindigkeit $v_{\text{Reaktion}}$ liegt:
das Problem liegt in der Länge des Zeitintervalls begründet, welches wir wählen. Je länger dieses ist, desto ungenauer wird die Reaktionsgeschwindigkeit, die wir ermitteln. Warum dies so ist, kannst du an den beiden folgenden Schaubildern nachvollziehen. Wir betrachten jeweils einen Ausschnitt der oben stehenden Abbildung:

Abb. 6: Unterschiedliche Bestimmung der Reaktionsgeschwindigkeiten

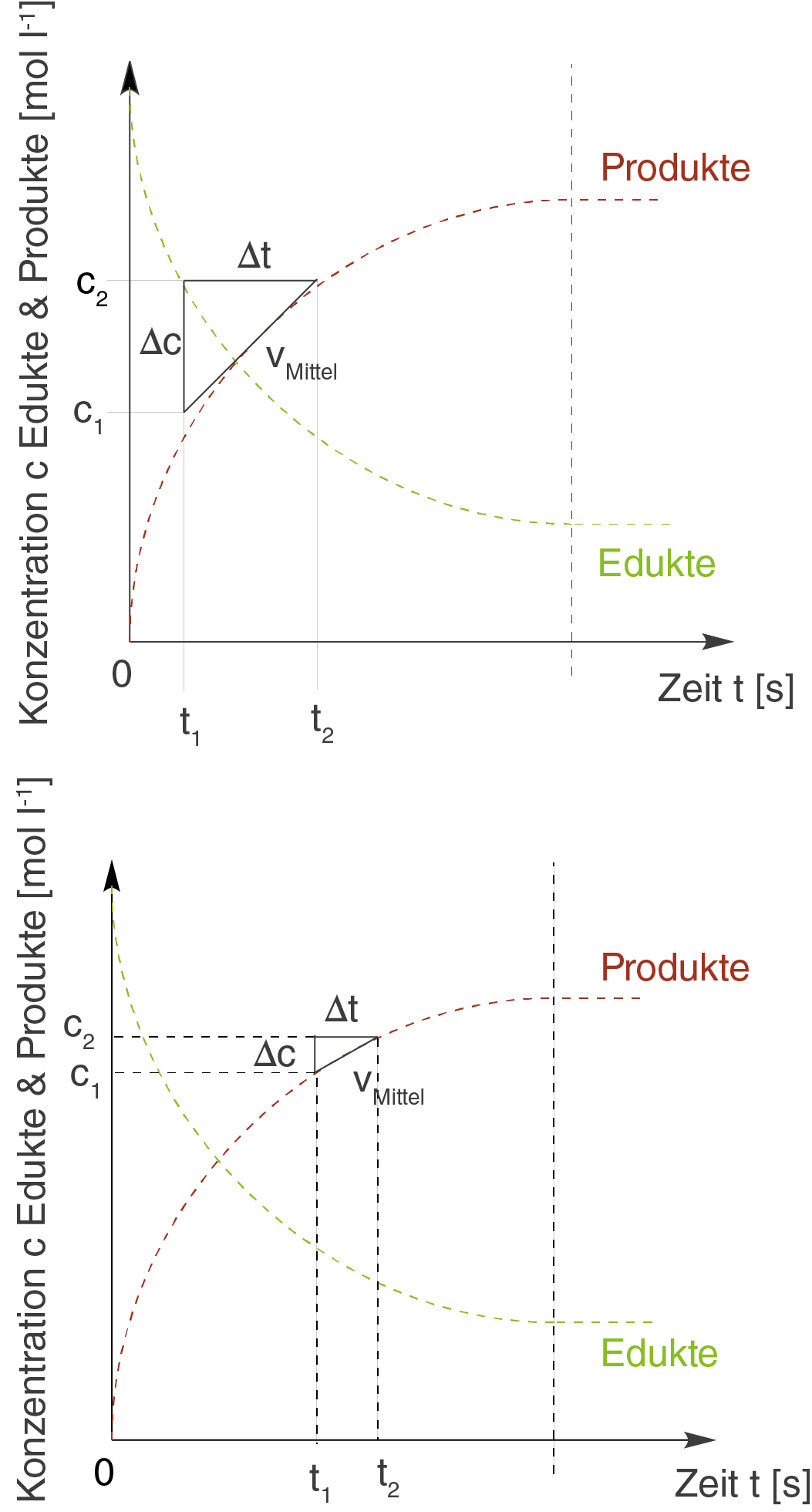
Wenn du die beiden Schaubilder vergleichst, dann kannst du sehen, dass die Hypothenuse des Steigungsdreiecks im linken sehr viel schlechter dem Kurvenverlauf entspricht, als im rechten. Je kürzer die Hypothenuse demnach ist, desto besser approximiert sie den Kurvenverlauf und desto besser können auch Änderungen im Verlauf der Kurve dargestellt werden.
Da die Länge der Hypothenuse mit der Länge der beiden Katheten zusammenhängt, können wir sie ändern wenn wir die Katheten ändern. Diese entsprechen aber gerade unseren gewählten Konzentrations- und Zeitänderungen $\Delta c$ und $\Delta t$ .
Um das bestmögliche Ergebnis für die Reaktionsgeschwindigkeit zu erhalten, die momentane Reaktionsgeschwindigkeit $v_{\text{Reaktion}}$ zum Zeitpunkt t, verkleinern wir das Zeitintervall so weit es geht. Wenn wir den oben eingeführten Formalismus verwenden, können wir schreiben:

$v_{\text{Reaktion}}$ = $\displaystyle\lim\limits_{\Delta t\to 0}\dfrac{\Delta c}{\Delta t}$ = $\dfrac{dc}{dt}$

Hier steht nicht mehr, als dass wir das Zeitinterval $\Delta t$ infinitesimal klein (kleiner geht nicht mehr) werden lassen, so dass es letztendlich aber noch von null verschieden ist. Es kommt hier nicht auf den nummerischen Wert an, den das Zeitintervall besitzt, sondern nur, dass es infinitesimal klein ist.
Damit beschreibt $\dfrac{dc}{dt}$ die Änderungsrate der Konzentration eines Reaktanden und die Hypothenuse in unseren Steigungsdreiecken, welche die Kurve approximiert, schrumpft auf einen Punkt zusammen.
Wenn wir an dieser Stelle wieder auf die Definition der Reaktionsgeschwindigkeit vom Beginn des Kapitels zurückgreifen, erhalten wir folgende Gleichung:

$v_{\text{Reaktion}}$ = $\dfrac{dc}{dt}$ = $k\cdot c_{\text{A}}\cdot c_{\text{B}}$

Es geht hier nicht darum, dass du diese Gleichung lösen kannst, dass übersteigt den Schulstoff, sondern dass du siehst, um was es sich bei der Reaktionsgeschwindigkeit handelt. Nämlich um einen zeitlich Änderung der Konzentrationen der Edukte.

Kinetisch gehemmte Systeme (metastabile Systeme)

Wie du bisher sehen konntest, hängt die Reaktionsgeschwindigkeit $v_{Reaktion}$ von den Konzentrationen $c$ der Edukte und dem Geschwindkeitskoeffizienten $k$ ab. Es gibt nun aber auch solche Reaktionen, deren Reaktionsgeschwindigkeit bei Normalbedingungen extrem klein ist. Das bedeutet, dass effektiv keine Reaktion stattfindet.
Im Vergleich zu den Gleichgewichtssystemen, die wir bisher betrachtete haben und als stabile Systeme bezeichnen können, werden diese als kinetisch gehemmte oder auch metastabile Gleichgewichtssysteme bezeichnet. Diese Reaktionsklasse kann durch energetische Aktivierung zur Reaktion gebracht werden. Wir werden dies nun an einem Beispiel genauer erläutern.
Wir betrachten folgende Gleichgewichtsreaktion:

$\text{H}_{2\,\text{(g)}}+\frac{1}{2}\,\text{O}_{2\,\text{(g)}}$ $\rightleftharpoons$ $\text{H}_{2}\text{O}_{\text{(l)}}$

Diese Reaktion ist auch als Knallgasreaktion bekannt. Warum es sich bei dieser Reaktion jedoch um eine kinetisch gehemmte Reaktion handelt, können wir nicht an der Reaktionsgleichung erkennen. Dazu müssen wir ein wenig auf die Energetik schauen und nach der Aktivierungsenergie dieser Reaktion fragen:

Abb. 7: Unterschiedliche Aktivierungsenergien

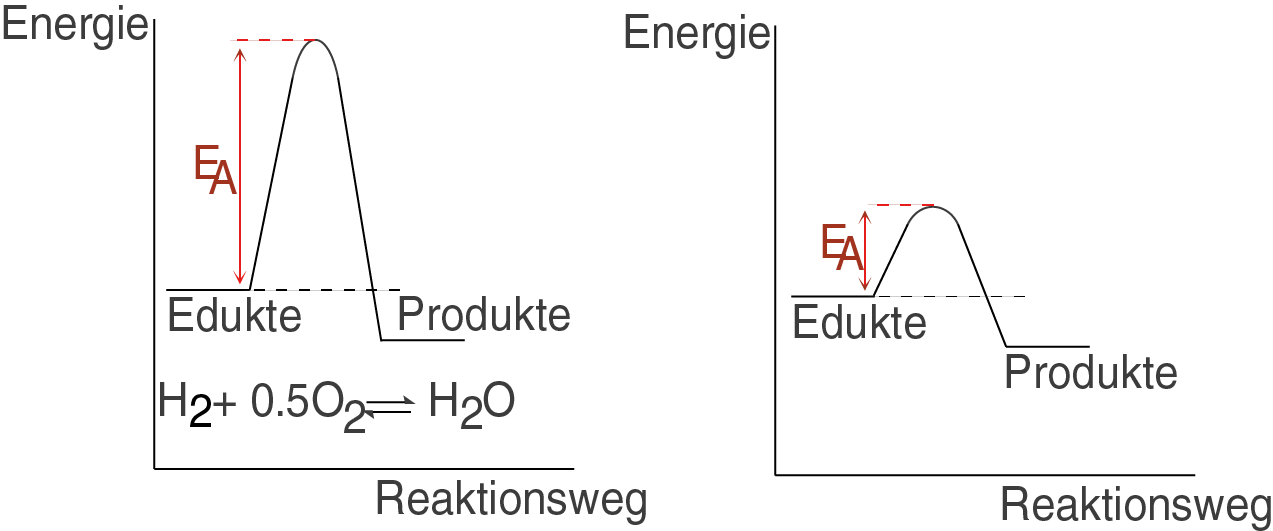
Das linken Schaubild veranschaulicht uns die energetische Situation der Knallgasreaktion: sie benötigt eine hohe Aktivierungsenergie, was bei Normalbedingungen quasi nicht möglich ist. Sie ist kinetisch gehemmt.
Das rechte Schaubild veranschaulicht hingegen die energetische Situation eines stabilen Gleichgewichtssystems mit geringer Aktivierungsenergie.
Wie kinetisch gehemmte Gleichgewichtsreaktionen dennoch zur Reaktion gebracht werden können, werden wir uns im nächsten Kapitel genauer anschauen. Dort werden wir das Konzept der Katalyse besprechen und den Begriff des Katalysators einführen.

Bildnachweise [nach oben]

[1]

[2]

[3]

[4]

[5]

[6]

[7]