In diesem Skript beschäftigen wir uns mit den Grenzen der energetischen Betrachtung. Jede Theorie hat, sowohl was ihren Inhalt betrifft, als auch was ihre Aussagekraft und Aussagemöglichkeiten betrifft, eigene Grenzen. Innerhalb dieser Grenzen ist die Theorie anwendbar und kann bedeutende Ergebnisse liefern. Irgendwann sind die vorhandenen Kapazitäten jedoch erschöpft und die Grenzen der Theorie erreicht. So verhält es sich auch mit der chemischen Energetik.

Wir wollen kurz darauf eingehen, was du dir unter den Grenzen einer Theorie vorstellen kannst. Der naturwissenschaftlich arbeitende Mensch beschreibt Prozesse, die er in der Natur findet in einem Rahmen, der es ihm möglich macht diese noch zu begreifen. Prinzipiell geht es darum, dass wir als Mensch immer dazu gezwungen sind zu abstrahieren. Das bedeutet, wir sind nicht in der Lage alle Einzelheiten eines betrachteten Problems gedanklich zu erfassen. Diese Abstraktion führt dazu, dass wir beginnen systematisch zu denken. Die Einführung von Grenzen macht es uns möglich den Betrachtungsgegenstand für den menschlichen Verstand in gewisser Weise fassbar zu machen. Dahinter steckt der Systemgedanke, mit Systemen als durch den Menschen wohl definierte abstrakte Gebilden. Wir schaffen uns die Möglichkeit Prozesse verstehen zu können. Die Beschreibung dieser Prozesse ist aber folglich ebenso abstrahiert, wie auch ihre Betrachtungsweise. Das bedeutet, dass die Theorie an sich, die den Inhalt der Beschreibung ausmacht, auch an Grenzen stoßen wird. Außerhalb dieser Grenzen ist es entweder nicht mehr sinnvoll die Theorie anzuwenden, weil beispielsweise Grundannahmen nicht mehr gelten, oder andere Prozesse beginnen zu dominieren, die im Kanon der aufgestellten Theorie nicht berücksichtigt sind und somit auch keinen Untersuchungsgegenstand darstellen können.

In diesem Skript wollen wir diese Grenzen an den Beispielen der Metastabilen Zustände und der unvollständig ablaufenden Reaktionen besprechen.

Metastabile Zustände

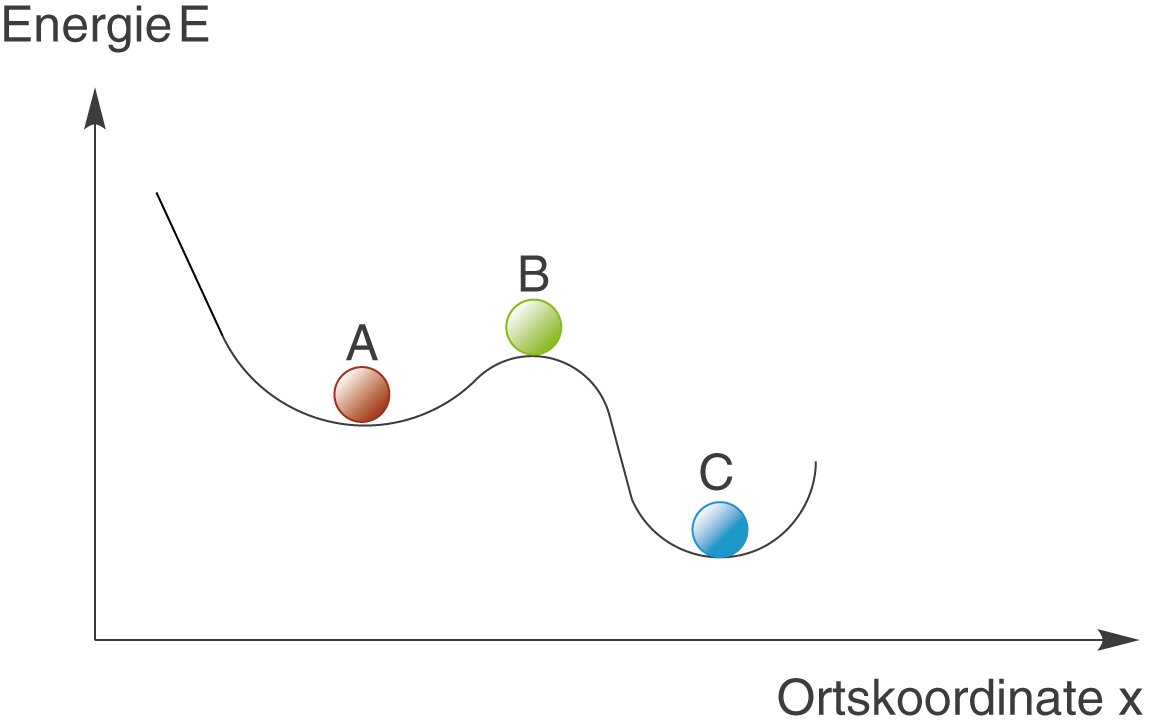
Der Begriff der Metastabilität beschreibt einen Zustand, der gegenüber kleinen Änderungen stabil ist, jedoch instabil gegenüber großen Veränderungen. Wir wollen uns diesen Begriff anhand der folgenden Graphik klar machen:

• A: metastabil Kleine Änderung ändert den Zustand der roten Kugel über grün nach blau.
• B: labil Die grüne Kugel wird diesen Zustand in jedem Fall verlassen.
• C: stabil Die blaue Kugel befindet sich im energetisch günstigsten Zustand.

Wir betrachten einen Ball, der an drei unterschiedlichen Positionen eines Berghangs zu finden sein kann. Diese Positionen werden durch die Bezeichnungen A, B und C beschrieben. Gleichzeitig betrachten wir die Lage des Balls auch unter energetischen Gesichtspunkten. Eine Vertiefung im Hang stellt dabei ein energetisches Minimum dar. Du siehst, hier gibt es zwei solcher Minima, wobei das rechte dominanter ist. Die Position A steht sinnbildlich für einen metastabilen Zustand: Eine kleine Anstrengung wird nicht dazu führen, dass der Ball aus der Vertiefung herausfällt. Wenn wir jedoch ein wenig mehr Aufwand betreiben, dann können wir den Ball aus dem Zustand A in den Zustand B versetzen und von dort rollt er den Hügel hinab. Letztendlich bekommen wir den stabilsten der drei Zustände: Zustand C.

Ein metastabiler Zustand zeichnet sich dadurch aus, dass er gegenüber geringen Änderungen stabil ist, gegenüber großen Änderungen jedoch instabil

Metastabile Reaktionen sind insbesondere solche, die kinetisch gehemmt sind (vgl. Skript Reaktionsgeschwindigkeit). Das bedeutet, dass diese Reaktionen unter energetischen Gesichtspunkten zwar ablaufen könnten, die Reaktionsgeschwindigkeit aber extrem gering ist. Das Problem ist hierbei, dass eine relativ hohe Aktivierungsenergie notwendig ist, um entsprechende Reaktionen zum Ablaufen zu bringen.

Beispiel 1: Reaktion von Sauerstoff mit Holz

Die Verbrennung von Holz (hier allg. organische Verbindung ):

Diese Reaktion benötigt eine gewisse Aktivierungsenergie, damit sie abläuft, obwohl sie exergon () ist. Das entspricht unserer Alltagserfahrung: Holz beginnt nicht einfach zu brennen, sondern wir müssen es anzünden.

Beispiel 2: Knallgasreaktion

Eine weitere prominente Reaktion, die kinetisch gehemmt ist, ist die Knallgasreaktion.

Obwohl diese Reaktion exergon ist (), ist die Mischung von Wasserstoff und Sauerstoff bei Raumtemperatur stabil. Sobald jedoch auch nur ein kleiner Funke entsteht, wird diese Reaktion explosiv unter Bildung von Wasser ablaufen.
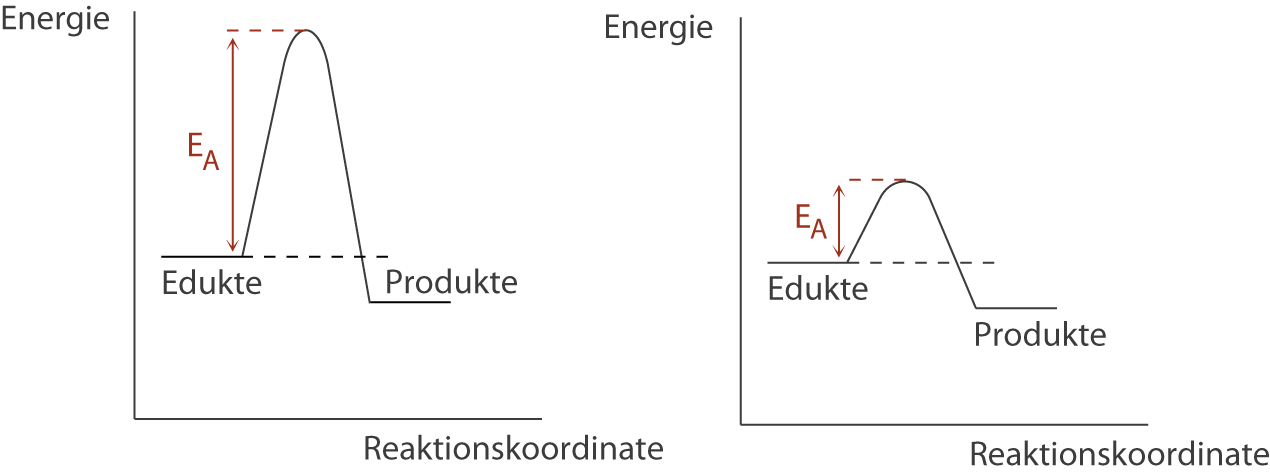
Wir wollen nun noch einen Blick auf die energetische Situation dieser Reaktionen richten:

Rechts sehen wir die energetische Situation einer geringen Aktivierungsenergie . Eine solche Reaktion ist ungehemmt und kann bereits bei relativ geringen Aktivierungsenergien ablaufen. Im linken Schaubild wird genau das Gegenteil veranschaulicht: Die Aktivierungsenergie ist sehr groß und die Reaktion muss entweder durch eine solche, extern bereitgestellte, oder durch den Einsatz eines Katalysators (vgl. Skript Der Katalysator) zur Reaktion gebracht werden . Ansonsten ist die Reaktionsgeschwindigkeit sehr gering.

Die Theorie der chemischen Energetik trifft für beide Beispielreaktionen oben (die Verbrennung von Holz und die Knallgasreaktion) eine eindeutige Aussage: Die Reaktionen sind exergon und laufen somit unter energetischen Gesichtspunkten freiwillig ab. Dies ist aber nicht der Fall, wie wir sehen konnten. Die chemische Energetik liefert uns hier keine Möglichkeit das beobachtete Verhalten adäquat zur erklären. Es steht im Widerspruch zur Theorie - die theoretischen Grenzen sind erreicht. Um dieses Problem zu verstehen, müssen wir die Theorie der chemischen Energetik verlassen und uns der Kinetik chemischer Reaktionen zuwenden, da letztere Aussagen über deren Geschwindigkeit trifft. Diese Tatsache entspricht dem Aspekt, den wir bereits in der Einleitung dieses Skripts angesprochen haben. Vom Menschen aufgestellte Theorien sind abstrakte Vorstellungen, die Grenzen aufweisen müssen, damit wir sie gedanklich in einer gewissen Weise erfassen können. Darum gibt es viele unterschiedliche Theorien zu unterschiedlichen Sachverhalten.

Unvollständige Reaktionen

Im letzten Abschnitt dieses Skripts wollen wir uns mit einer weiteren Idealisierung beschäftigen, die nicht der Realität entspricht. Reaktionen laufen normalerweise nicht so ab, wie uns unsere Reaktionsgleichungen sagen. Sehr viele Reaktionen laufen unvollständig ab. Die Reaktionsgleichung entspricht einem Idealbild. Wir wollen hier noch einmal auf ein Beispiel zurückgreifen, das wir hier bereits behandelt haben: Die Verbrennung von Holz.
Idealerweise, dass heißt, wenn alle Reaktanden stöchiometrisch vorhanden sind, läuft diese Reaktion so ab:

Die organischen Verbindungen, die das Holz aufbauen, reagieren komplett mit Sauerstoff zu Wasser und Kohlenstoffdioxid. Wenn du dich nun an eigene Erfahrungen erinnerst, dann wird dir auffallen, dass bei einem Lagerfeuer nach dem Verbrennen in keinem Fall nur diese beiden Verbindungen zurückbleiben. Daneben liegt auch immer noch eine Menge Feststoff, in Form von Asche, vor. Weiterhin wird während des Verbrennungsvorgangs neben dem bereits erwähnten auch bspw. frei.
Du siehst, schon ein vermeindlich einfacher Prozess, wie eine Verbrennung, kann durch unsere Reaktionsgleichung nicht realitätstreu dargestellt werden, sondern eben sehr idealisiert. Wenn wir alle anderen Reaktionen, die bei einer solchen Verbrennung von Holz auftreten können, auch noch beachten würden, dann würde sich die Komplexität des Problems erheblich erhöhen. In der Realität entsteht eine Vielzahl von verschiedenen Produkten.

Da unsere energetischen Betrachtungen aber von diesen idealen Bedingungen ausgehen, müssen wir uns auch dessen bewusst sein, dass wir nur idealisierte Ergebnisse erhalten werden. Je realitätstreuer das Ergebnis werden soll, desto komplexer wird die Herangehensweise und die Behandlung des Problems. Die Grenzen der energetischen Betrachtung werden also auch durch den Komplexitätsgrad der Betrachtung bestimmt: Je „einfacher“ wir ein Problem behandeln, also je idealer, desto idealer und „ungenauer“ wird auch das Ergebnis. Damit erreichen wir auch hier die Grenzen der Theorie.