Azofarbstoffe und die Absorption

Definition

In diesem Skript beschäftigen wir uns mit einer wichtigen Gruppe von Farbstoffen, den Azofarbstoffen. Diese verdanken ihren Namen der Azogruppe $\text{R}_{1}-\text{N}=\text{N}-\text{R}_{2}$ , die wir uns noch genauer anschauen wollen.

Abb. 1: Die Natur kennt so viele Farben

Um die Azofarbstoffe verstehen zu können, müssen wir uns zunächst um den Begriff der Farbigkeit kümmern. Fragen, die es zu beantworten gilt, beziehen sich auf die Eigenschaften des „farbigen“ Lichts sowie dessen Rolle als Bestandteil des elektromagnetischen Spektrums. Kennen wir diese Eigenschaften und den Zusammenhang zwischen der Farbe des Lichts und seiner Energie, dann können wir uns mit dem Kern des ersten Abschnitts beschäftigen: der Anregung von Elektronen. Diese Prozesse sind zentral für das Verständnis der Azofarbstoffe und ihrer farbgebenden Eigenschaften.

Im dritten Abschnitt wenden wir uns dann den Azofarbstoffen zu. Wir beschäftigen uns zunächst mit deren Grundaufbau sowie der Synthese, um im Anschluss die relevanten Eigenschaften anzusprechen, die die Farbigkeit hervorrufen. In diesem Zusammenhang verwenden wir dann die Grundlagen, die wir in Abschnitt 2 erarbeitet haben. Abschließend interessiert uns dann der Einfluss von Substituenten auf die Farbigkeit der Azofarbstoffe.

Im letzten Kapitel dieses Skripts beschäftigen wir uns dann mit einem Phänomen, dass dir bereits bekannt ist, bis jetzt aber nicht erklärt werden konnte: der Farbumschlag von pH-Indikatoren im Kontext der Azofarbstoffe.

Anmerkung:
Wenn wir in diesem Skript von Strahlung reden, dann meinen wir immer elektromagnetische Strahlung, auch wenn es manchmal nicht dabei steht!

Absorption von Licht

Elektromagnetische Stahlung und Energie

Sichtbares Licht im elektromagnetischen Spektrum

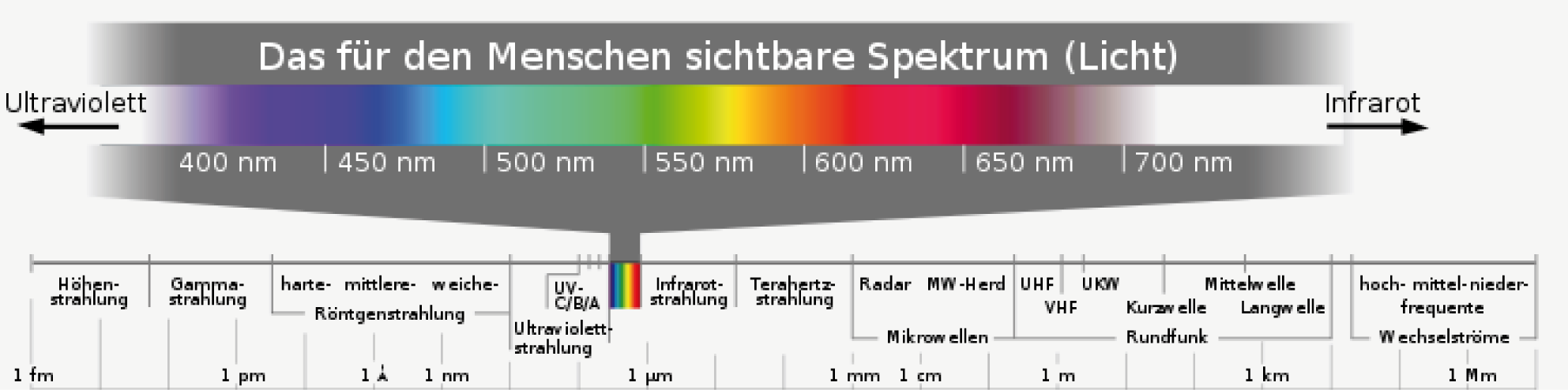
Wenn wir über Licht reden, dann meinen wir den Wellenlängenbereich des elektromagnetischen Spektrums, den wir mit unseren Augen wahrnehmen können. Das elektromagnetische Spektrum umfasst alle Wellenlängen $\lambda$ , die eine elektromagnetische Welle annehmen kann. Diese Wellenlängen werden gewöhnlich in Nanometer ( $1\,\text{nm}=10^{-9}\,\text{m}$ ) angegeben (vgl. Abb. 2).

Abb. 2: Für den Menschen sichtbares Spektrum im elektromagnetischen Spektrum

In Abbildung 2 kannst du den Ausschnitt des elektromagnetischen Spektrums sehen, den wir als Licht bezeichnen. Dieser Bereich umfasst ca. die Wellenlängen $\lambda$ von $350 \,\text{nm}$ (violett) bis $700\,\text{nm}$ (rot) und wird abgekürzt auch als VIS-Bereich bezeichnet (von engl. visible). Werden die Wellenlängen kürzer als $350\,\text{nm}$ , dann befinden wir uns im Bereich der Ultraviolettstahlung (kurz UV-Strahlung). Im Fall von Wellenlängen, die größer als $700\,\text{nm}$ sind erreichen wir den Bereich der Infrarotstrahlung (IR-Strahlung).

Uns interessiert in diesem Skript aber insbesondere der VIS-Bereich. Um zu verstehen, warum das so ist, müssen wir uns zunächst mit der Energie der Strahlung beschäftigen.

Zusammenhang zwischen Energie und Wellenlänge der Strahlung

In den 20er Jahren des 20. Jahrhunderts fand Albert Einstein heraus, dass Licht nicht nur einen Wellencharakter hat, sondern auch als ein Strom von „kleinen Energiepaketen“ betrachtet werden muss. Diese Energiepakete nennen wir Photonen. Die Energie $E$ dieser Photonen hängt von der Wellenlänge $\lambda$ der jeweiligen elektromagnetischen Strahlung ab. Für die Energie $E$ eines Photons gilt:

$E\sim\dfrac{1}{\lambda} \text{bzw} E=\dfrac{h\cdot c}{\lambda} \text{mit} h\cdot c=const.$

Zunächst sehen wir, dass die {Energie $E$ des Photons proportional zum Inversen der Wellenlänge ist. Um zu klären, was das konkret bedeutet, wollen wir uns ein kleines Beispiel anschauen. Dazu betrachten wir Strahlung aus dem VIS-Bereich mit einer Wellenlänge von $\lambda_{\text{VIS}}=500\,\text{nm}$ (grünes Licht) und Strahlung aus dem UV-Bereich mit einer Wellenlänge von $\lambda_{\text{UV}}=50\,\text{nm}$ . Die Wellenlängen können wir nun oben einsetzen:

$E_{\text{VIS}}=\dfrac{h\cdot c}{\lambda_{\text{VIS}}} \Leftrightarrow E_{\text{VIS}}=\dfrac{h\cdot c}{500\,\text{nm}}$

$E_{\text{UV}}>=\dfrac{h\cdot c}{\lambda_{\text{UV}}} \Leftrightarrow E_{\text{UV}}=\dfrac{h\cdot c}{50\,\text{nm}}$

Die Energie $E_{\text{VIS}}$ des sichtbaren Lichts (VIS) ist viel kleiner, als die Energie $E_{\text{UV}}$ des UV-Lichts. Die Konstanten $h$ und $c$ stehen auf beiden Seiten, interessieren uns hier also gar nicht weiter.

$E_{\text{VIS}}=\dfrac{h\cdot c}{500\,\text{nm}} \dfrac{h\cdot c}{50\,\text{nm}}=E_{\text{UV}}$

Das bedeutet, dass die Energie der Photonen mit zunehmender Wellenlänge abnimmt. Je langwelliger das Licht, desto energieärmer ist es!

Anmerkung:
Bei den Konstanten handelt es sich um das Plancksche Wirkungsquantum $h$ und die Lichtgeschwindigkeit $c$ .

Wir halten also folgende Informationen fest, die wir später noch benötigen werden:

Einstein fand heraus, dass Licht neben seinen Welleneigenschaften auch als Strom von Teilchen, den sogenannten Photonen, beschrieben werden muss.
Photonen sind gleichsam „kleine Energiepakete“, die eine wohldefiniert Energiemenge tragen.
Die Energie $E$ eines Photons hängt von der Wellenlänge $\lambda$ der jeweiligen Strahlung ab und ergibt sich zu $E=\dfrac{h\cdot c}{\lambda}$ .

Anmerkung:
Versuche dir bitte nicht vorzustellen wie und wieso Licht gleichzeitig Teilchen - und Welleneigenschaften aufweisen kann. Das ist nicht möglich und bringt dich hier auch nicht weiter. Merke dir das Konzept der Energiepakete; dieses hilft dir im Weiteren sehr anschaulich die Probleme zu verstehen.

Anregung von Elektronen

$\blacktriangleright$ Der Begriff der Anregung

Wir wollen uns nun um die sogenannte Anregung von Elektronen kümmern. Wenn wir davon sprechen ein Elektron anzuregen, dann versetzen wir dieses Elektron in einen Zustand höherer Energie. Im ChemieLV-Skript Atommodelle und die Elektronenstruktur von Atomen haben wir uns bereits mit diesem Begriff beschäftigt. Dort ging es uns darum, Elektronen im Rahmen des Bohrschen Atommodells von einer Bahn auf eine andere anzuheben. Dieses Vorhaben konnten wir durch die Zufuhr von Energie bewerkstelligen. Dieses Konzept der Anregung wollen wir hier ebenfalls verwenden.

Achtung:
Wir verwenden hier das gleiche Konzept wie beim Bohrschen Atommodell. Wir verwenden aber in keinem Fall das Bohrsche Atommodell an sich, um uns hier etwas zu erklären. Es geht nur darum zu verstehen, was sich hinter dem Begriff der Anregung eines Elektrons verbirgt.

$\blacktriangleright$ Diskrete Energieniveaus

Bei der Anregung geht es uns hier aber nicht um die Bahnen von Elektronen im Bohrschen Atommodell, sondern etwas abstrakter einfach um zwei unterschiedliche Energieniveaus. Im ChemieLV-Skript Atommodelle und die Elektronenstruktur von Atomen sehen wir, dass eine Elektron nicht jede beliebige Energie annehmen kann, sondern auf bestimmte festgelegte Werte beschränkt ist. In diesem Zusammenhang spricht man auch davon, dass die Energieniveaus von Elektronen diskret sind und nicht kontinuierlich. Du kannst dir das ganze ungefähr wie eine Leiter vorstellen (vgl. Abb. 3).

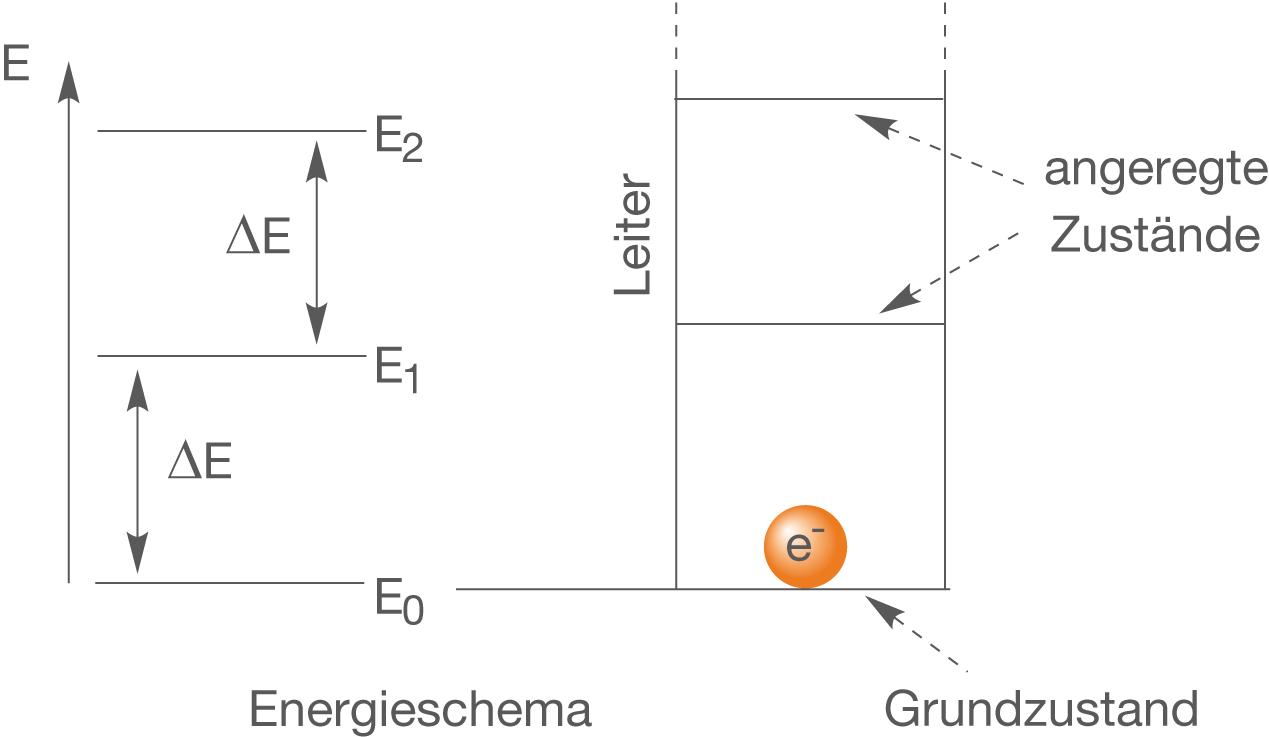
Abb. 3: Energieschema und die Analogie zur Leiter

Rechts siehst du die Analogie zur Leiter. Der energieärmste Zustand entspricht dem, den das Elektron einnimmt, wenn es am Fuß der Leiter sitzt. Wir sprechen in diesem Zusammenhang auch vom Grundzustand des Elektrons.

Heben wir das Elektron durch die Zufuhr einer Energiemenge $\Delta E$ auf das nächste Energieniveau, dann entspricht dies im übertragenen Sinn dem Erklimmen der ersten Sprosse auf der Leiter. Diesen neuen Zustand bzgl. der Energie des Elektrons bezeichnet man als angeregten Zustand.

Die Sprossen einer Leiter weisen immer einen wohldefinierten Abstand voneinander auf. Ganz analog dazu verhalten sich die Energieniveaus, die ein Elektron einnehmen kann. Das bedeutet dann, dass ein Elektron eben nicht alle beliebigen Energieniveaus einnehmen kann, sondern eben nur sehr bestimmte festgelegte. Es handelt sich also nicht um eine kontinuierlichen sondern um einen diskreten Verlauf der Energieniveaus.

$\blacktriangleright$ Photonen und angeregte Zustände

Wir haben bisher noch nicht eindeutig geklärt, wie wir Elektronen aus ihrem Grundzustand in einen angeregten Zustand überführen. Hier kommt nun das Licht und die Photonen ins Spiel. Wir wissen folgendes:

Licht muss in bestimmten Situationen auch als ein Strom von Photonen verstanden werden, die wir als Energiepakete auffassen können.
Um ein Elektron in einen angeregten Zustand zu heben, benötigen wir eine bestimmte Energiemenge $\Delta E$ .

An dieser Stelle kommen wir nun auf den Begriff des Energiepakets zu sprechen. Diese können nämlich nicht jede beliebige Energie tragen, sondern immer nur ein Vielfaches des planckschen Wirkungsquantums $h$ . Unter „Zusammenhang zwischen Energie und Wellenlänge der Strahlung“ haben wir folgenden Zusammenhang gesehen:

$E=\dfrac{h\cdot c}{\lambda}$ $\quad$ $\text{womit}$ $\quad$ $E\sim h$ $\quad$ $\text{mit}$ $\quad$ $h=6,626\cdot10^{-34}\,\text{Js}$

$E\sim h$ bedeutet, dass $E$ proportional zu $h$ ist und das ist genau der Punkt, der uns hier interessiert: Die Energie eines Photons kann nicht jeden beliebigen Wert annehmen, sondern nur Vielfache des planckschen Wirkungsquantums $h$ und letzteres ist wie bereits erwähnt konstant. Das bedeutet, dass wir es im Fall von Photonen mit diskreten Energiepaketen zu tun, also solchen die wohldefiniert Energiemengen mit sich herum tragen.

Trägt ein solches Photon eine Energiemenge $E$ , die der Energiedifferenz $\Delta E$ zwischen zwei Energieniveaus entspricht, dann kann dieses Photon ein Elektron von einem Energieniveau auf das andere anregen. Dabei geht das Photon mit seiner Energiemenge quasi auf das Elektron über, es wird absorbiert. Erinnere dich hier an die Analogie der Sprossen einer Leiter, um den Prozess der Anregung zu verbildlichen.

Azofarbstoffe

Die Azofarbstoffe sind eine spezielle Gruppe von synthetischen Verbindungen, die den folgenden charakteristischen Aufbau besitzen (vgl. Abb. 4).

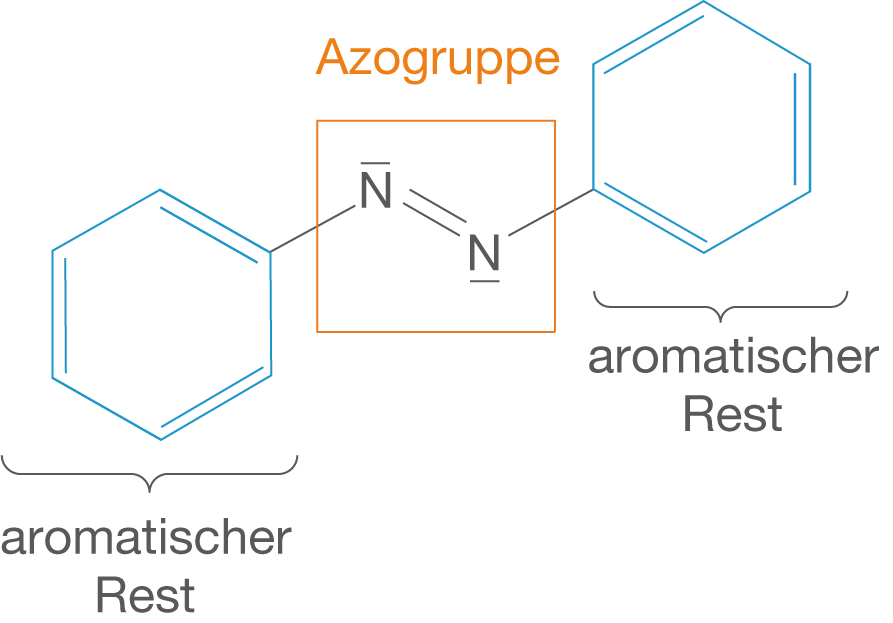
Abb. 4: Molekülstruktur der Azofarbstoffe mit Azo-Gruppe

An den aromatischen Resten können weitere unterschiedliche Substituenten sitzen, deren Einfluss auf die Farbigkeit wir später noch sehen werden. Zunächst beschäftigen wir uns mit der Synthese der Azofarbstoffe.

Synthese: Diazotierung und Azokupplung

Diazotierung

Den erste Schritt, den wir bei der Synthese eines Azofarbstoffes betrachten müssen, ist die Diazotierung. Unser Ziel ist es hier das Diazonium-Kation zu gewinnen, welches wir später als Edukt für die Bildung des Azofarbstoffes benötigen.

$\blacktriangleright$ Darstellung des Nitrosyl-Kations

Im ersten Schritt lassen wir ein Nitrit-Anion ( $\text{NO}_{2}^{-}$ ) mit $\text{H}^{+}$ unter Abspaltung von Wasser zum Nitrosyl-Kation ( $\text{NO}^{+}$ ) reagieren (vgl. Abb. 5).

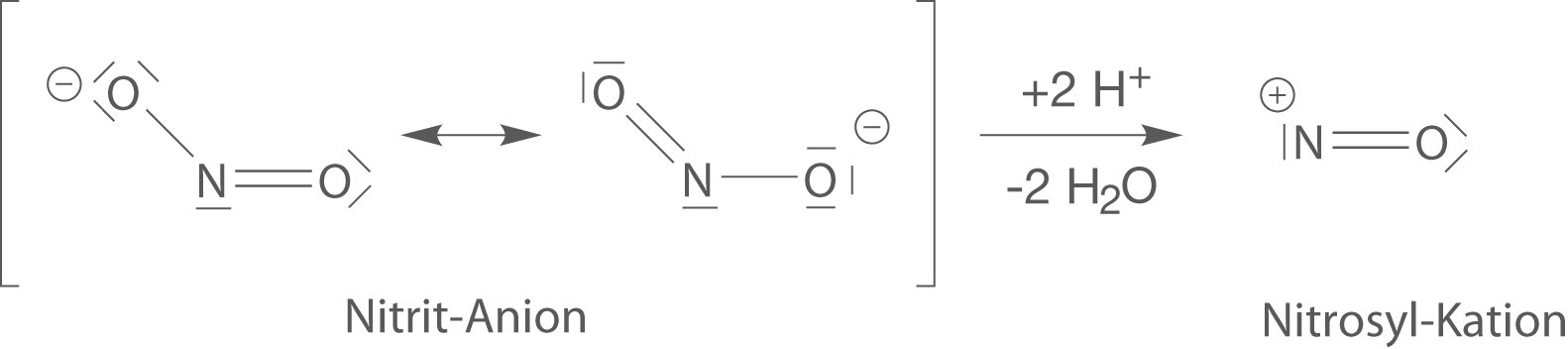
Abb. 5: Darstellung des Nitrosyl-Kations

Das Nitrosyl-Kation trägt eine positive Ladung, womit es ganz besonders gerne mit Verbindungen reagiert, die freie Elektronenpaare aufweist. Solche Verbindungen nennen wir Elektrophil.

$\blacktriangleright$ Darstellung des Diazonium-Kations

Dieses elektrophile Nitrosyl-Kation lassen wir in einem zweiten Schritt mit Anilin zum Diazonium-Kation reagieren.

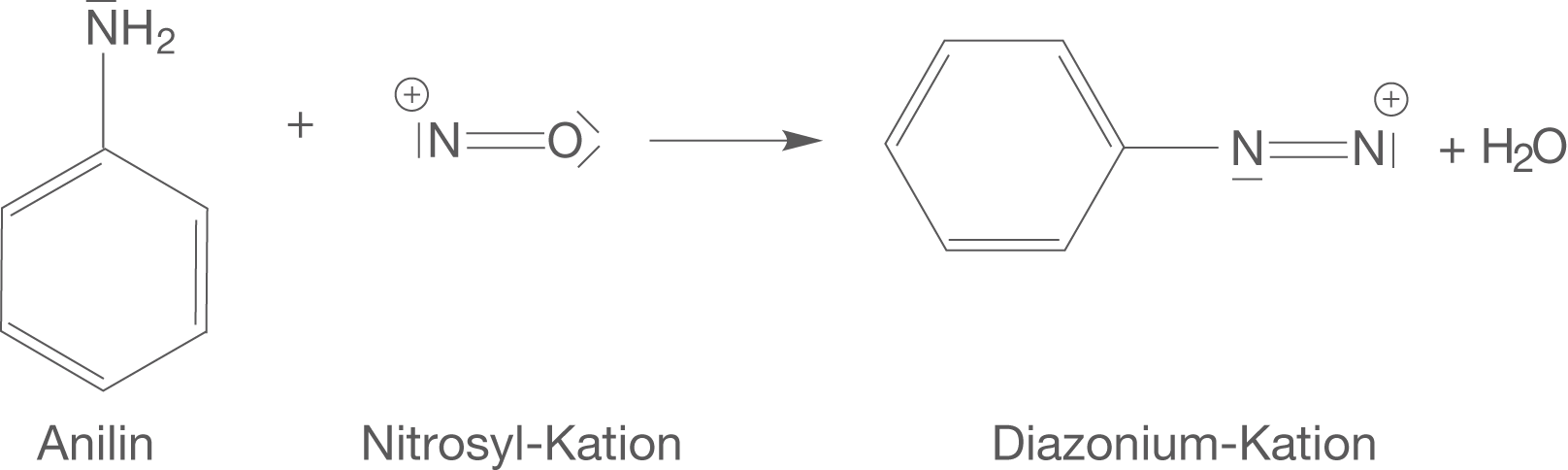
Abb. 6: Darstellung des Diazonium-Kations mit den Edukten Anilin und dem Nitrosyl-Kation

Das Diazonium-Kation verwenden wir nun für die Azokupplung, um den Azofarbstoff zu synthetisieren. Bedenke: Das Diazonium-Kation ist wieder ein Elektrophil, da es eine positive Ladung trägt.

Azokupplung

Die Azokupplung beschreibt die Reaktion des wiederum elektrophilen Diazonium-Kations mit einer elektronenreichen aromatischen Komponente. In diesem Fall handelt es sich also um eine elektrophile Substitution am Aromaten (vgl. ChemieLV-Skript Aromaten). Wir wählen als zweites Edukt wieder Anilin. Der Phenylrest ist sehr elektronenreich und kann mit dem elektrophilen Diazonium-Kation reagieren.

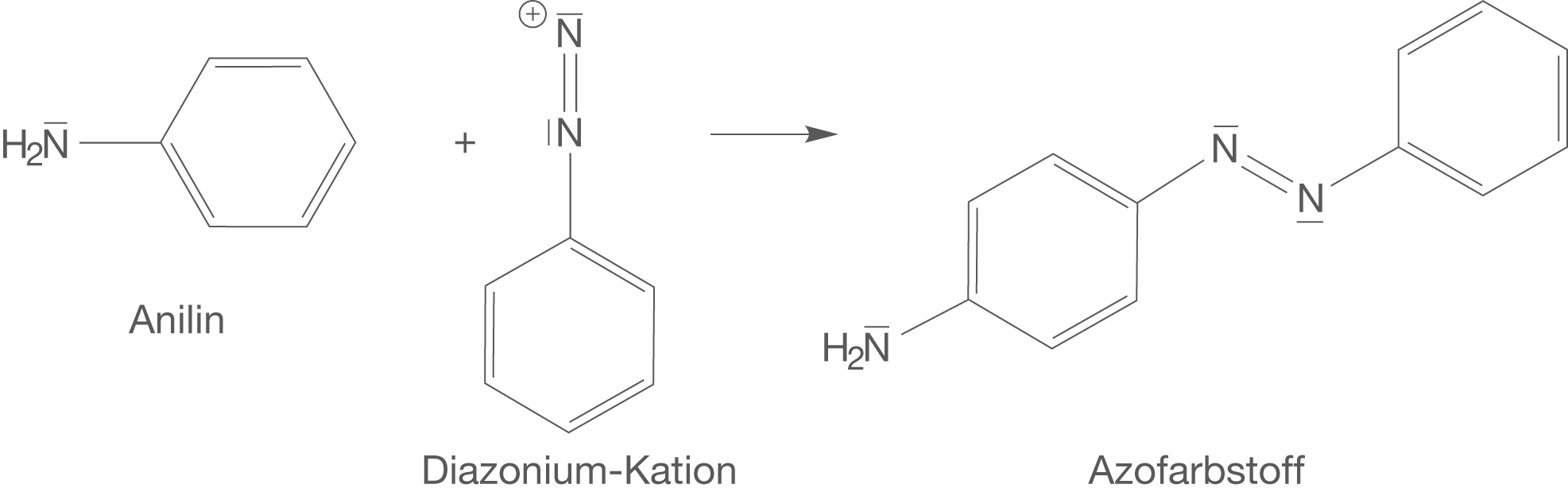
Abb. 7: Darstellung eines Azofarbstoffes mittels Azokupplung

Wir erhalten einen Azofarbstoff mit der charakteristischen Azogruppe $(\text{R}_{1}-\text{N}=\text{N}-\text{R}_{2})$ . Nun wollen wir uns den optischen Eigenschaften dieser Moleküle zuwenden und ihre Wechselwirkung mit Licht ansprechen.

Farbigkeit: Eigenschaften des $\pi$ -Elektronen-Systems

Im Zentrum dieses Abschnitts steht das $\pi$ -Elektronen-System und seine Eigenschaften bzgl. der Anregung durch Licht. Wichtig ist, dass wir in diesem Zusammenhang auch von delokalisierten $\pi$ -Elektronen reden, die wir einerseits von den Aromaten kennen, die andererseits aber auch in Molekülen mit konjugierten Doppelbindungen vorliegen.

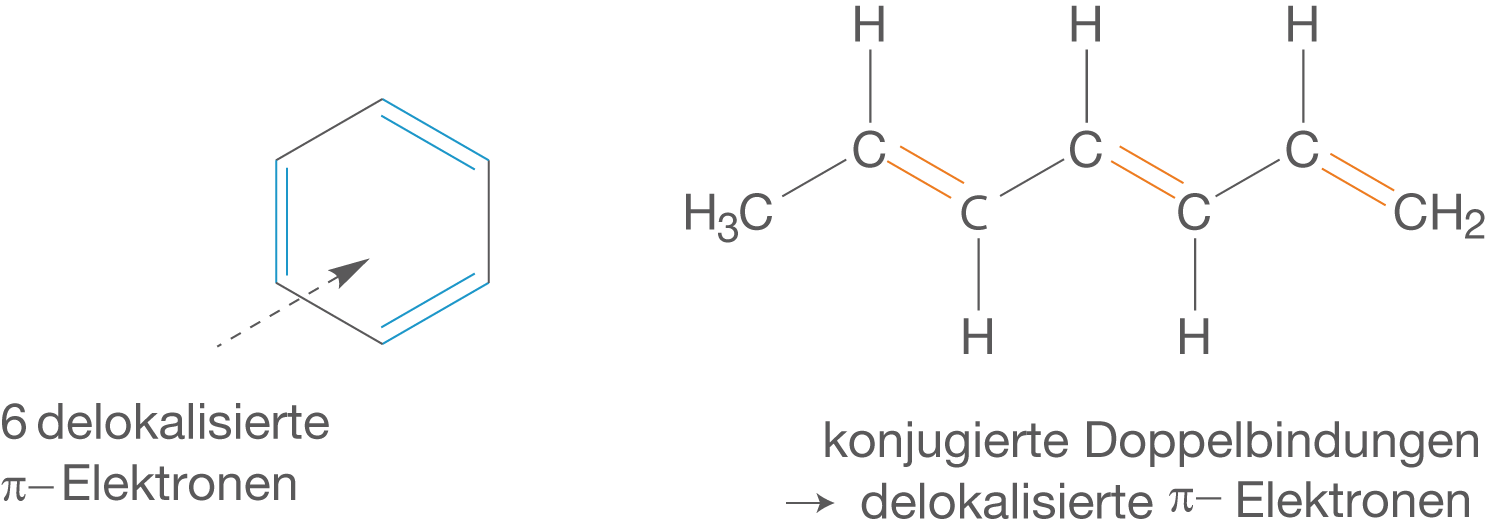
Abb. 8: Delokalisierte u-Elektronen in Aromaten und konjugierten Systemen

Diese $\pi$ -Elektronen können wir nach den Prinzipien aus „Anregung“ von Elektronen mithilfe von Licht anregen. Bevor wir uns um die Details kümmern wollen und die Größe des $\pi$ -Elektronensystems als relevanten Faktor kennen lernen, wollen wir zunächst klären, was der Begriff der Farbigkeit bedeutet.

Wir betrachten hier nur sichtbares Licht (VIS). Dieses setzt sich aus einem Spektrum von Wellenlängen $\lambda$ zusammen, die von ca. $350\,\text{nm}$ bis $700\,\text{nm}$ reichen. Der Begriff des Spektrums beschreibt die Gesamtheit dieser Wellenlängen. Wenn wir aus dem Fenster schauen, dann sehen wir eine farbige Welt. Den Umstand, der jedem Objekt seine Farbe zuschreibt, können wir folgendermaßen erklären: Alle Objekte absorbieren Licht einer bestimmten Wellenlänge des sichtbaren Spektrums. Damit fehlt diese Wellenlänge und somit auch effektiv diese Farbe im Spektrum des sichtbaren Lichts. Die Farbe eines Objekts, die wir sehen können kommt also daher, dass wir genau die Strahlung zu sehen bekommen, die sich nur noch aus den übrig gebliebenen Wellenlängen zusammensetzt. Ein konkretes Beispiel wäre die grüne Farbe von Pflanzen. Diese absorbieren Licht im roten und blauen Wellenlängenbereich des Spektrums, womit das grüne Licht übrig bleibt.

$\blacktriangleright$ $\pi$ -Elektronen und Anregung durch Licht

Nun sind wir soweit, dass wir einerseits die Theorie der Anregung von Elektronen und andererseits die Moleküle der Azofarbstoffe zusammenbringen können, um die Farbigkeit zu erklären.

Wir wissen, dass die Energie des Lichts in Form von wohldefinierten Energiepaketen, den Photonen, vorliegt. Die Energie dieser Photonen ist wie in dem Kapitel „Zusammenhang zwischen Energie und Wellenlänge der Strahung“ gesehen abhängig von der Wellenlänge des Lichts, wobei diese wiederum die die Farbe des Lichts festlegt. An dieser Stelle sei schon erwähnt, dass wir die $\pi$ -Elektronen der Azofarbstoffe mit Strahlung im sichtbaren Bereich des elektromagnetischen Spektrums anregen können. Den dritten Punkt, den wir uns hier wieder in Gedanken rufen müssen, ist die diskrete Abfolge der Energieniveaus, die Elektronen besetzen könne. Hier war es wichtig, dass nur gewisse Energiebeträge absorbiert werden können, die effektiv zu einer Anregung führen.

Wir wollen die Folgen nun anhand von Abbildung 9 klären.

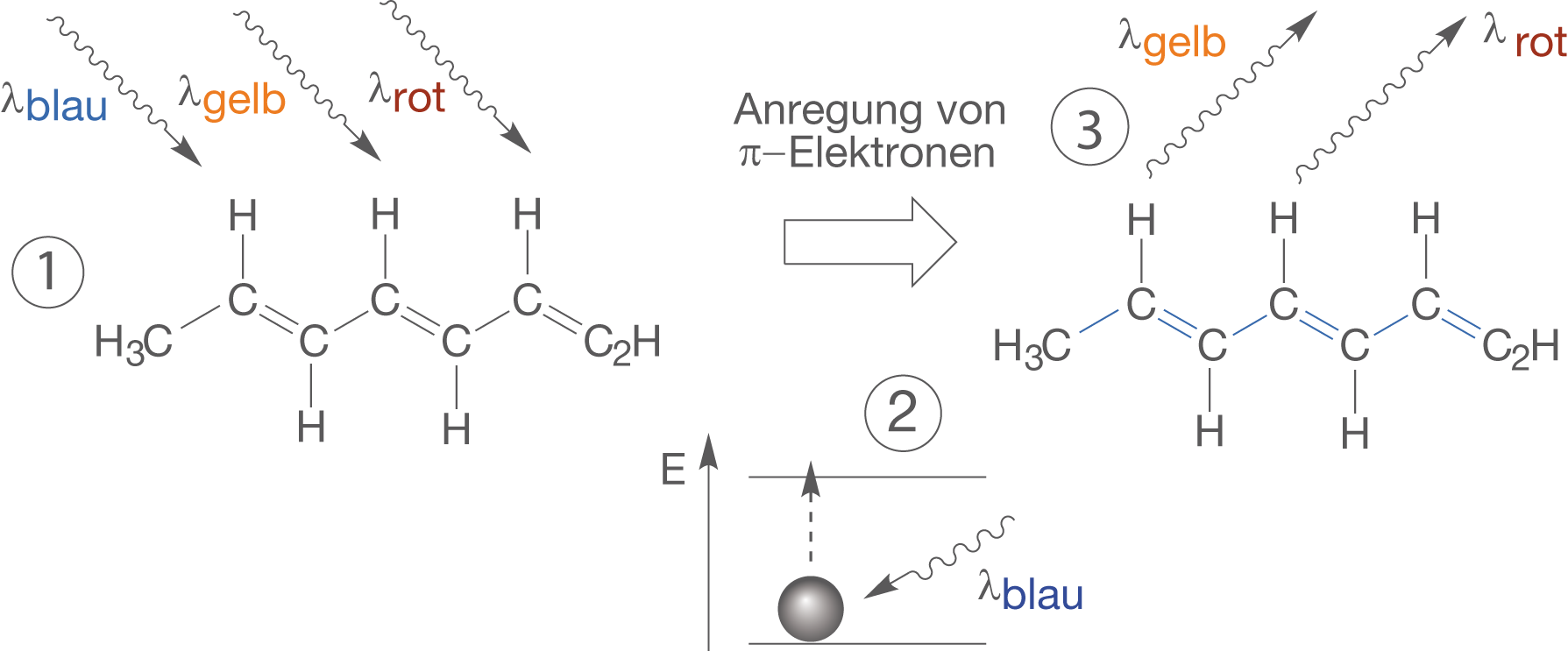
Abb. 9: Farbigkeit, hervorgerufen durch die Absorption spezifischer Wellenlängen

Im Folgenden sind die einzelnen Schritte erklärt:

Wir regen die delokalisierten $\pi$ -Elektronen eines Systems konjugierter Doppelbindungen mit Licht an, dass sich grob aus blauem ( $\lambda_{\text{blau}}$ ), gelbem ( $\lambda_{\text{gelb}}$ ) und rotem Licht ( $\lambda_{\text{rot}}$ ) zusammensetzt.
Für die Anregung der delokalisierten $\pi$ --Elektronen kommt nur das energiereichste blaue Licht in Frage, weshalb dieses absorbiert wird. Diese Wellenlänge fehlt nun im Spektrum (Gesamtheit aller Wellenlängen) unseres Lichts.
Dadurch, dass das rote und gelbe Licht übrig bleibt und reflektiert wird, hat unsere Verbindung in diesem Fall ungefähr eine orange Farbe. Diese lässt sich als Mischung der beiden anderen verstehen.

$\blacktriangleright$ Das Chromophor: Die Azo-Gruppe

Eine Atomgruppierung, die für die Farbigkeit eines Moleküls verantwortlich ist, nennt man Chromophor. Im Fall der Azofarbstoffe ist die Azo-Gruppe in Zusammenspiel mit den aromatischen Resten das Chromophor. Dort haben wir ein System delokalisierter $\pi$ -Elektronen vorliegen, die sich durch Licht im sichtbaren Bereich des elektromagnetischen Spektrums anregen lassen.

$\blacktriangleright$ Einfluss der Größe des $\pi$ -Elektronen-Systems auf die Anregungsenergie

Wenn wir uns $\pi$ -Elektronen-Systeme anschauen, dann beobachten wir folgenden Effekt: Die Anregungsenergie der $\pi$ -Elektronen nimmt mit zunehmender Größe des Systems ab. Das bedeutet konkret, dass der Energiebetrag, den wir für die Anregung aufwenden müssen kleiner wird: Der energetische Abstand zwischen dem Grundzustand und dem angeregten Zustand schrumpft mit zunehmender Größe des $\pi$ -Elektronen-Systems.

Die Folge daraus bezieht sich auf die notwendigen Energien, die zur Anregung der $\pi$ -Elektronen notwendig sind. Wird der Abstand der beiden Energieniveaus mit zunehmender Molekülgröße kleiner, dann benötigen wir nur noch eine geringere Energiemenge, um ein Elektron aus einem Zustand in den anderen anzuregen. Demzufolge ist hier nun auch energieärmeres Licht für die Anregung möglich. Die Energie des Lichts nimmt mit zunehmender Wellenlänge ab (vgl. 2.2). Je größer das Farbstoffmolekül, desto weiter ist die Wellenlänge des zur Anregung notwendigen Lichts in Richtung rotes Licht verschoben.

Substiuenteneinfluss: Auxochrome und antiauxochrome Reste

Auxochrome und antiauxochrome Reste

Wenn du hier noch einmal einen Blick auf das Produkt der Azokupplung aus Abbildung 7 wirfst, dann kannst du sehen, dass wir dort am linken aromatischen Ring einen Rest hängen haben: die Aminogruppe $\text{R}-{NH}_{2}$ . Diesen können wir natürlich auch gegen einen anderen Substituenten austauschen, wie bspw. eine Hydroxygruppe R-OH oder wir können auch weitere Substituenten am aromatischen Rest anhängen. Hier kommen wir nun auf die Einflüsse dieser Reste auf die Anregungsenergien der $\pi$ -Elektronen zu sprechen. Wir unterscheiden dabei auxochrome und antiauxochrome Reste.

Auxochrome Reste sorgen dafür, dass das $\pi$ -Elektronen-System vergrößert wird und somit die Anregungsenergie sinkt. Dieser Effekt ist dadurch möglich, dass diese Substituenten Elektronenpaare bereitstellen (Elektronendonatoren). Diese Eigenschaft äußert sich darin, dass diese Moleküle einen mesomeren Effekt (kurz +M-Effekt) mit sich bringen. Dieser vergrößert das System der delokalisierten Elektronen indem er direkt die mesomere Struktur des Moleküls beeinflusst. Wir können diese Gruppen beim formulieren der mesomeren Grenzformeln miteinbeziehen. Solche Substituenten sind beispielsweise die bereits erwähnte Aminogruppe R- $\text{NH}_{2}$ und die Hydroxygruppe R-OH.

Antiauxochrome Reste sind dahingegen Substituenten, die einen -M-Effekt aufweisen; sie entziehen dem System Elektronen (Elektronenakzeptoren). Wichtig ist, dass die antiauxochromen Reste nur im Zusammenspiel mit den auxochromen Resten ihre Wirkung entfalten und dann auch einen farbverstärkenden Effekt aufweisen. Sollten sie alleine vorkommen, dann wird ein solcher Effekt nicht beobachtet. Ein Beispiel eines antiauxochromen Rests ist die Nitrogruppe R- $\text{NO}_{2}$ .

Optimaler Weise ist der Azofarbstoff so aufgebaut, dass an einem Ende eine auxochrome Gruppe und am anderen Ende die antiauxochrome Gruppe zu finden ist. Dazwischen befindet sich das System der delokalisierten $\pi$ -Elektronen.

Farbverschiebung: Bathochromer und hypsochromer Effekt

Während die Adjektive auxochrom und antiauxochrom die Eigenschaften der Substituenten beschreiben, werden die daraus resultierenden Effekte als bathochromer und hypsochromer Effekt bezeichnet.

Der bathochrome Effekt beschreibt die Verschiebung der zur Anregung eines $\pi$ -Elektrons notwendigen Wellenlänge von Licht in Richtung größerer Wellenlängen. Er wird deshalb auch als Rotverschiebung bezeichnet. Gehen wir diese Aussage an den folgenden Punkten durch:

Auxochrome und Antiauxochrome Reste führen zu einem farbverstärkenden Effekt.
Die Anregungsenergie der $\pi$ --Elektronen sinkt aufgrund der Vergrößerung des $\pi$ -Elektronen-System, was auf den +M-Effekt des auxochromen Rests zurückgeht.
Das Resultat ist ein Absinken der Anregungsenergie der $\pi$ -Elektronen, was gleichbedeutend damit ist, dass das zur Anregung notwendige Licht langwelliger sein kann. Je langwelliger das Licht, desto weiter kommen wir in den roten Bereich des sichtbaren Spektrums.

Bisher hatten wir nur den Fall, dass das System der delokalisierten $\pi$ -Elektronen vergrößert wurde, was mit einer Absenkung der Anregungsenergien einherging. Der hypsochrome Effekt beschreibt nun das Resultat einer Verkleinerung des Systems delokalisierter $\pi$ -Elektronen: die Anregungsenergie nimmt zu. Wir beobachten in diesem Fall eine Verschiebung der Wellenlängen hin zum blauen Ende des sichtbaren Spektrums.

Azofarbstoffe und ihre Rolle als pH-Indikatoren

Säure-Base-Chemie von Methylorange

$\blacktriangleright$ Methylorange

Im letzten Kapitel dieses Skripts wollen wir uns mit der Anwendung der Azofarbstoffe in Form von pH-Indikatoren beschäftigen. In diesem Zusammenhang geht es uns nun um die pH--Abhängigkeit der Farbe einer solchen Verbindung. Als Beispielverbindung wählen wir Methylorange (vgl. Abb. 10).

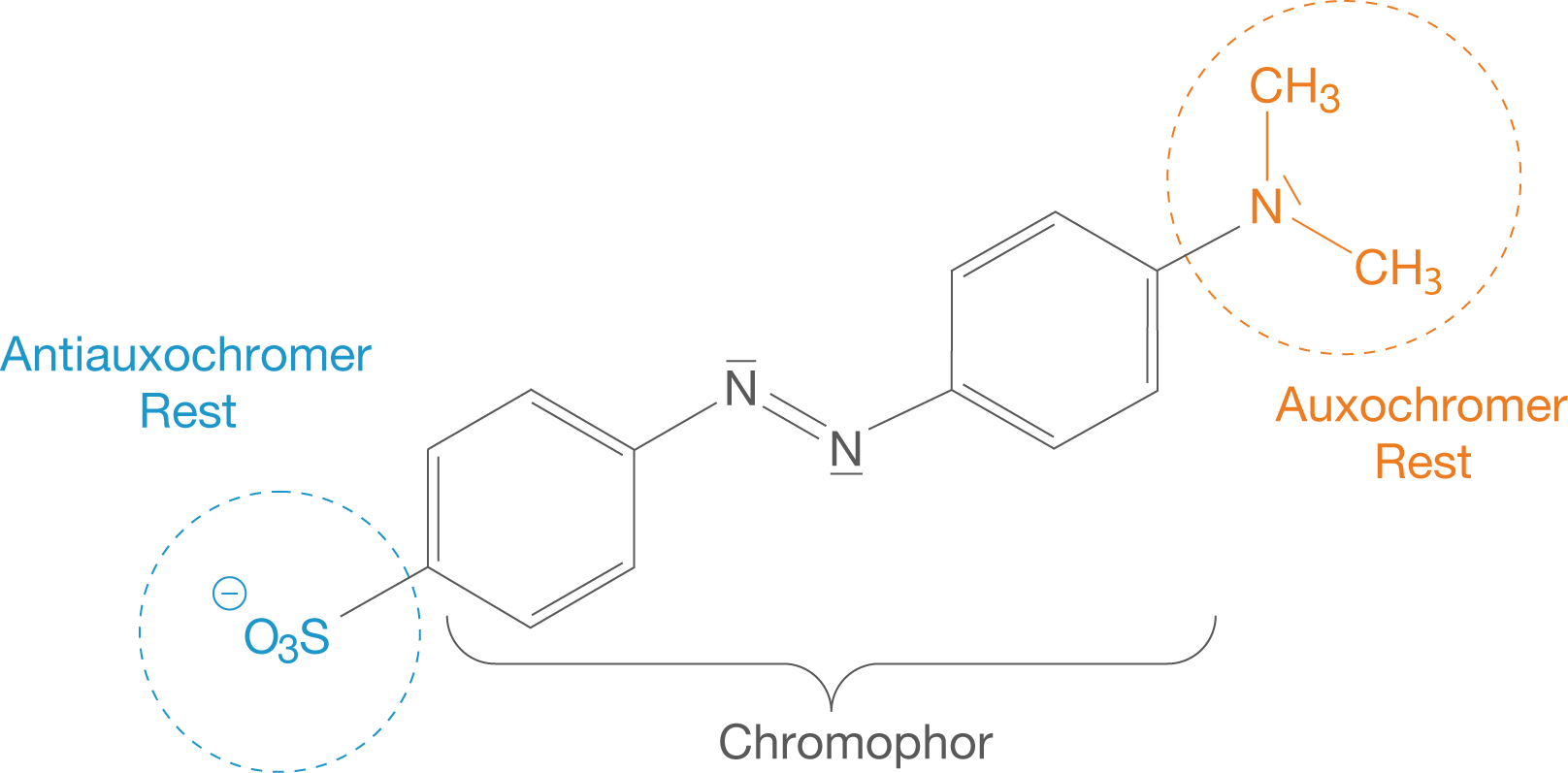
Abb. 10: Methylorange mit auxochromem und antiauxochromem Rest

Du kannst sehen, dass Methylorange eine negative Ladung trägt, was es als Salz identifiziert. Das in Abbildung 10 fehlende Gegenion ist das Natriumkation ( $\text{Na}^{+}$ ).

$\blacktriangleright$ Säure-Base-Chemie von Methylorange

Bringen wir Methylorange mit einer Säure HA zur Reaktion, dann wird das N-Atom der Azo-Gruppe, welches sich näher an der $\text{SO}_{3}^{-}$ -Gruppe befindet, protoniert (vgl. Abb. 11).

Abb. 11: Protonierung von Methylorange

Wenn wir uns die Eigenschaften dieses Indikators anschauen, dann finden wir einen Umschlagsbereich zwischen pH 3,1 und pH 4,4. Das bedeutet konkret, dass Methylorange bei sauren pH-Werten protoniert und bei pH--Werten mit $\text{pH}>4,4$ deprotoniert vorliegt.

Mesomeriestabilisierung und Farbigkeit

Was wir uns beim Einsatz von pH--Indikatoren wie Methylorange zu nutze machen, ist die optische Unterscheidbarkeit der protonierten und der deprotonierten Form. Auf der Grundlage der Anregung delokalisierter $\pi$ -Elektronen können wir den Farbumschlag nun erklären.

$\blacktriangleright$ Der Farbumschlag als Änderung der Anregungsenergie

Zunächst wollen wir uns damit beschäftigen, was der Farbumschlag vor dem Hintergrund der Anregung von Elektronen für eine Bedeutung hat. Wir wissen bereits, dass wir das Licht zu sehen bekommen, welches sich aus allen nicht absorbierten Wellenlängen im sichtbaren Bereich des elektromagnetischen Spektrums zusammensetzt. Ändert sich die Farbe des Indikators, dann muss sich folglich auch die Wellenlänge des absorbierten Lichts geändert haben.

$\blacktriangleright$ Mesomeriestabilisierung als Auslöser

Der Auslöser für den Farbumschlag ist die unterschiedliche Mesomeriestabilisierung der protonierten sowie der deprotonierten Form von Methylorange.

Betrachten wir die mesomeren Grenzformeln der deprotonierten Form, dann erhalten wir folgendes Bild (vgl. Abb. 12):

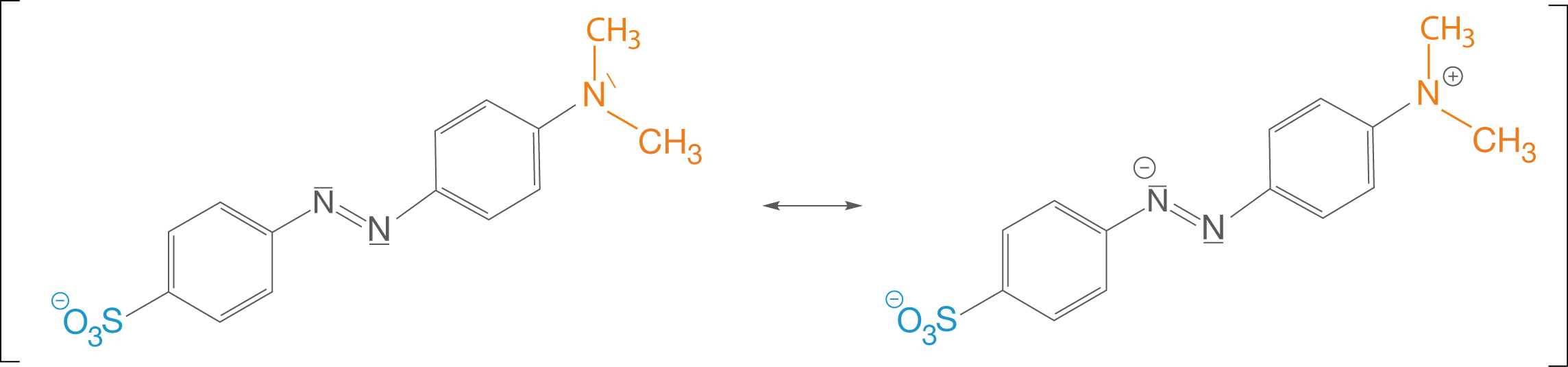
Abb. 12: Mesomere Grenzformeln der deprotonierten Form

Wir halten fest, dass sich im Fall der rechten Grenzformel eine Ladungstrennung ergibt. Nun werfen wir einen Blick auf die mesomeren Grenzformeln der protonierten Form (vgl. Abb. 13).

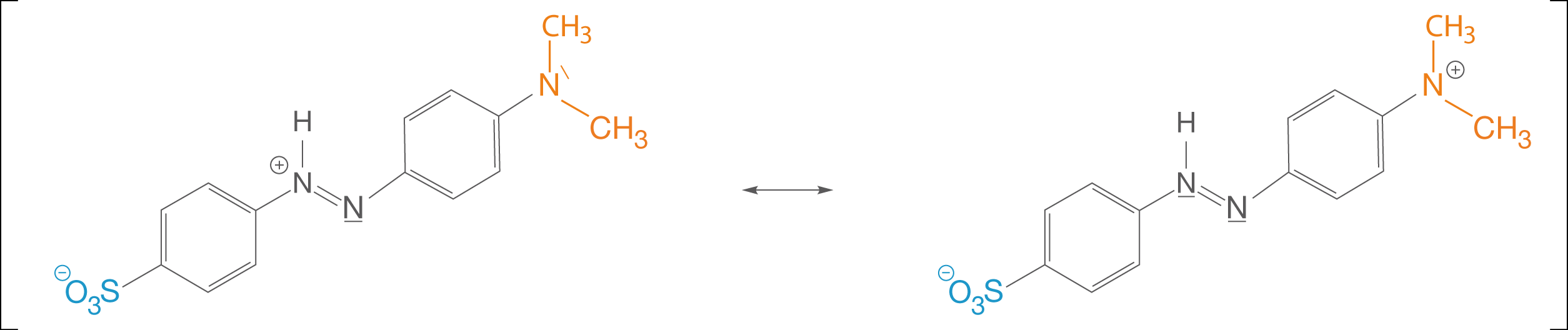
Abb. 13: Mesomere Grenzformeln der protonierten Form

Wenn wir uns die mesomeren Grenzformeln in Abbildung 13 anschauen, dann fällt uns auf, dass sich dort keine Ladungstrennung ergibt. Wir können nur beobachten, dass sich die positive Ladung vom N-Atom der Azo-Gruppe zum N-Atom der Dimethylamino-Gruppe gewandert ist.

Vergleichen wir diese beiden Fälle der Mesomeriestabilisierung, dann lässt sich folgendes Feststellen:

Die Ladungstrennung im deprotonierten Fall ist nicht besonders günstig, weshalb die Mesomeriestabilisierung des $\pi$ -Elektronen-Systems im deprotonierten Fall vergleichsweise gering ausfällt.
Im Fall der protonierten Form beobachten wir nur eine Ladungsverschiebung, die durch die Mesomeriestabilisierung hervorgerufen wird. Dieser Fall ist energetisch gesehen günstig und die Stabilisierung somit effektiv wirksam.
Die für die Anregung notwendige Energie des Lichts fällt im Fall der protonierten Form geringer aus, da das $\pi$ -Elektronen-System mesomeriestabilisiert ist. Die rote Farbe spricht dafür, dass hier Wellenlängen im grünen Bereich des sichtbaren Spektrums absorbiert werden.
Die Anregung der Elektronen in der deprotonierten Form benötigt energiereichere Strahlung. Da wir hier eine gelbe Färbung beobachten, können wir folgern, dass die absorbierte Strahlung aus dem kurzwelligeren blauen Bereich des Spektrums stammt.
Die Argumentation der Punkte 3 und 4 basiert auf dem Konzept der Komplementärfarben.

Zusammenfassung

Das sichtbare Licht umfasst ungefähr die Wellenlängen von $350\,\text{nm}$ bis $700\,\text{nm}$ im elektromagnetischen Spektrum.
Der Zusammenhang zwischen der Energie $E$ des Lichts und seiner Wellenlänge $\lambda$ ergibt sich zu $E\sim\dfrac{1}{\lambda}$ .
Einstein fand heraus, dass Licht auch als Teilchenstrom aufgefasst werden muss. Diese Teilchen nennen sich Photonen und tragen eine wohldefinierte Energiemenge.
Mit zunehmender Wellenlänge nimmt die Energie eines Photons und damit die des Lichts ab (vgl. Punkt 2).
Elektronen können verschiedene Energiezustände annehmen. Der niedrigste ist der Grundzustand. Alle energetisch gesehen höher gelegenen werden als angeregte Zustände bezeichnet.
Um ein Elektron vom Grundzustand in einen angeregten Zustand zu überführe ist genau die Energiemenge notwendig, die die beiden Energieniveaus auseinander liegen.
Azofarbstoffe sind an der Azo--Gruppe und den daran befindlichen aromatischen Resten zu erkennen. Die Synthese verläuft in zwei Schritten: erstens die Diazotierung und zweitens die Azokupplung.
Die unter Punkt 7 genannte Atomgruppierung bestimmt die Farbigkeit der Azofarbstoffe und wird Chromophor genannt. Grundlage sind die delokalisierten $\pi$ -Elektronen der Azo-Gruppe und der aromatischen Reste, die sich durch Wechselwirkung mit Licht anregen lassen.
Die Anregungsenergie der delokalisierten $\pi$ -Elektronen bestimmt die Farbe des Azofarbstoffs.
Auxochrome Reste (+M-Effekt) und antiauxochrome Reste (-M-Effekt) an den aromatischen Ringen des Chromophors beeinflussen die Farbigkeit zusätzlich.
Eine Rotverschiebung nennt man bathochromen Effekt und eine Blauverschiebung hypsochromer Effekt.
Azofarbstoffe wie Methylorange finden Anwendung als pH-Indikatoren.
Die Anregungsenergien der delokalisierten $\pi$ -Elektronen der protonierten und der deprotonierten Form von Methylorange unterscheiden sich energetisch aufgrund von Effekten der Mesomeriestabilisierung. Dadurch kommt der Farbumschlag zu Stande.

Bildnachweise [nach oben]

[1]

Public Domain

[2]