Energie

In diesem Skript wollen wir uns mit dem Energiebegriff und den für uns relevanten Energieformen beschäftigen.

Die Einheit der Energie: das Joule

Da die Energie eine sehr zentrale Größe in vielen Bereichen der Naturwissenschaften ist, ist auch ihre Einheit äußerst wichtig. Aus diesem Grund schauen wir uns diese zuerst an und schlüsseln auf welche SI-Einheiten dahinter stecken.

Anmerkung: Einheiten sind in der Schule oft scheinbar nur ein notwendiges Übel, das beim Rechnen nicht vergessen werden darf. Ohne Einheiten sind wir jedoch nur im Besitz nummerischer Werte, also von Zahlen, die uns aber keinen Hinweis auf die Größe geben, deren Dimension sie beschreiben. Wenn du beispielsweise sagst, dass das Glas Kekse 1 wiegt, dann kann das Gewicht 1 g, 1 kg oder 1 Tonne sein. Es ist also unheimlich wichtig die Einheiten einer Gröe in jedem Fall immer parat zu haben, wenn mit ihr gerechnet wird.

Die Energie besitzt die Einheit:

Joule: $1\,\text{J}=\text{kg}\cdot\dfrac{m}{s^{2}}\cdot m=\text{kg}\cdot\dfrac{m^{2}}{s^{2}}$

In Worten: Ein Joule ist ein Kilogramm mal Meter pro Quadrat durch Sekunde im Quadrat.

Arbeit, $W$

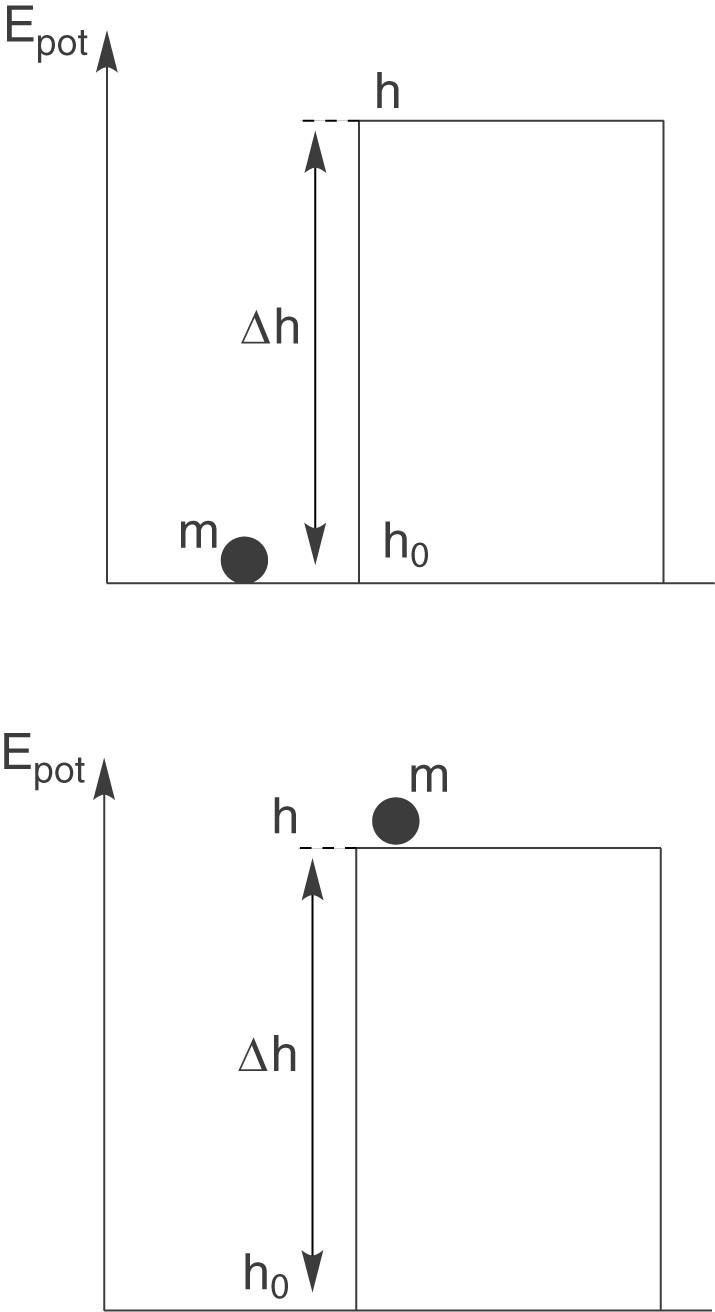
Als Arbeit bezeichnen wir eine Energiemenge, die bei einem Vorgang umgesetzt wird. Diese Tatsache können wir uns an folgendem Beispiel veranschaulichen:

Diagramm zur potentiellen Energie mit Höhenangaben und Masse. Illustrationen von h, m und Epot.

Abb. 1: Verrichtung von Arbeit

In der linken Graphik ist der Ball auf dem Boden dargestellt, während er im rechten auf den Schrank gehoben wurde. Zwischen der Position auf dem Boden und der auf dem Schrank besteht ein Unterschied in der potentiellen Energie, der Lageenergie, des Balls. Wir sagen, dass die potentielle Energie des Balls am Boden gleich null ist. Um den Energieunterschied zu berechnen, verwenden wir folgende Formel:

$\Delta E_{\text{pot}}$ = $E_{\text{pot, Schrank}}-E_{\text{pot, Boden}}$ = $m\cdot g\cdot h-m\cdot g\cdot h_{0}$ = $m\cdot g\cdot (h-h_{0})$ = $m\cdot g\cdot \Delta h$

Hierbei ist $E_{\text{pot}}$ die potentielle Energie, $m$ die Masse des Balls, $g$ die Gravitationsbeschleunigung der Erde und $h$ die Höhe des Schranks.

Du kannst sehen, dass der Energieunterschied im Höhenunterschied zwischen Boden und Schrank begründet liegt. Möchtest du diesen Ball auf den Schrank legen, dann musst du eine Anstrengung aufwenden, um den Ball soweit hoch zu heben, dass er auf dem Schrank zum liegen kommt. Diese nötige Energiemenge wird dem Ball im Form von Arbeit zugeführt. Du verrichtest Arbeit am Ball und erhöhst damit seine potentielle Energie. Da du hierbei den Zustand des Balls änderst, handelt es sich bei der Arbeit um eine Prozessgröße.

Wärmeenergie $Q$

Alle Materialien besitzen eine gewisse Temperatur, die sich vom absoluten Nullpunkt unterscheidet. Diese Energie ist folglich Teil eines jeden Körpers und eine Zustandsgröße. Bei einem idealen Gas können wir die kinetische Energie der Teilchen mit der Wärmeenergie gleichsetzen. Je schneller diese durch die Gegend fliegen, also je höher ihre kinetische Energie ist, desto höher ist auch die Temperatur.

Innere Energie $U$

Neben den bereits erwähnten Energieformen der Wärmeenergie und der Arbeit, wobei es sich bei letzterer eher um eine Energieänderung handelt, steht hier an dritter Stelle die Innere Energie. Dies ist die Energie, die in einer Verbindung gebunden ist. Dabei können verschiedene Teilkomponenten auftreten, die in der Summe diese Innere Energie $U$ ausmachen.
Die folgenden Energiebeiträge können zur Inneren Energie eines Systems beitragen:

mechanische Energie: $E_{\text{kin}}+E_{\text{pot}}$
Bindungsenergie
Schwingungsenergie
Rotationsenergie

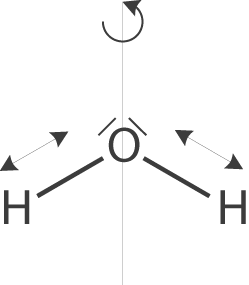
Beispielhafte Rotations- und Schwingungsbewegungen eines Wassermoleküls

Molekülstruktur mit Sauerstoff und Wasserstoffatomen, die eine Verbindung darstellen.

Abb. 2: Schwingungen und Rotation im Wassermolekül

Die Bindungsenergie beschreibt den Energiebetrag, welcher in den Bindungen gespeichert wird. Neben geradlinigen Bewegungen können Moleküle auch Schwingungs- oder Rotationsbewegungen durchführen. Sie fliegen also nicht nur durch den Raum, sondern drehen sich auch noch teilweise um ihre eigene Achse oder schwingen in allen möglichen Varianten. Auch diese Bewegungsformen weißen spezifische Energiebeträge auf.

Hauptsätze der Thermodynamik

Der 0. Hauptsatz der Thermodynamik beruht auf der Erfahrung des Menschen und ist nicht beweisbar. Er lautet:

0. Hauptsatz:

Wärme fließt spontan immer nur vom wärmeren zum kälteren Körper.

Zum besseren Verständnis sollen die folgenden Graphiken dienen. Wir haben dabei zwei Metallblöcke, wobei wir den einen Erhitzen, bevor wir ihn in Kontakt mit dem anderen bringen.

Diagramm mit Zeitpunkten T1, T0 und Tend sowie Pfeilen, die zeitliche Beziehungen darstellen.

Abb. 3: Wärmeausgleich

Bei diesem Experiment treten die beiden dargestellten Situationen auf:

Links: $T_{1}>T_{0}$ : kein thermisches Gleichgewicht $\rightarrow$ der rechte Block erwärmt sich.
Rechts: $T_{\text{end}}=const.$ : nach einer gewissen Zeit haben beide Blöcke die gleiche Temperatur; sie befinden sich im thermischen Gleichgewicht.

Der 1. Hauptsatz der Thermodynamik

Der erste Hauptsatz der Thermodynamik ist auch als Energieerhaltungssatz, kurz EES, bekannt. Er stellt einen der wichtigsten Grundpfeiler der modernen Naturwissenschaften dar.

1. Hauptsatz:

In einem abgeschlossenen System ist die Gesamtenergie konstant. Es kann keine Energie erzeugt oder vernichtet werden. Die verschiedenen Energieformen innerhalb des Systems können sich nur ineinander umgewandelt werden.

Wir können diesen Hauptsatz mit den bereits eingeführten Größen der inneren Energie $U$ , der Wärmeenergie $Q$ und der Arbeit $W$ auch in Form einer Gleichung schreiben:

$\Delta U=\Delta Q+\Delta W$

Die Änderung der Innere Energie des Systems setzt sich aus folgenden Größen zusammen:

$\Delta Q$ : die zugeführte oder abgeführte Wärmeenergie
$\Delta W$ : die am System verrichtete Arbeit bzw. die vom System verrichtete Arbeit

In einer anderen Formulierung heißt das, dass es keine Maschine gibt die Energie erzeugt, ohne dass ein Brennstoff Verwendung findet. Es gibt kein Auto, dass ohne eine Energiequelle, egal ob Benzin oder Strom, fährt. In diesem Zusammenhang wird auch davon gesprochen, dass die Energie innerhalb des Systems erhalten bleibt. Daraus leitet sich der Begriff des Energieerhaltungssatzes ab.

Da wir chemische Reaktionen idealisiert betrachten, also annehmen, dass sie in isolierten Systemen ablaufen, ist dieser Aspekt sehr wichtig für uns. Die Gesamtenergie in den Systemen, die wir betrachten ist folglich immer erhalten. Es wird also nie Energie in irgendeiner Weise verloren gehen, sondern nur zwischen verschiedenen Formen umgewandelt werden.

Bildnachweise [nach oben]

[1]

[2]

[3]