Anwendungen: Titration

Die Titration - Begriffserklärung

Die Titration ist eine experimentelle Methode der analytischen Chemie, die in den Bereich der quantitativen Analyse fällt. Das Wort Quantität kommt vom lat. quantitas und bedeutet Menge oder Größe. Die quantitative analytische Chemie fragt demnach nach der Menge eines Stoffes in einer bestimmten Probe. Neben dem „Was“ spielt also insbesondere das „Wieviel“ eine Rolle.

Im Falle der Titration werden unbekannte Stoffmengen in Lösungen ermittelt. Das Vorgehen bei einer Titration wollen wir ebenso wie deren Auswertung in diesem Kapitel erarbeiten. Dabei werden wir uns auf die Säure-Base-Titrationen beschränken, die du bereits aus der Schule kennst. Prinzipiell ist es dennoch wichtig, dass du im Hinterkopf behältst, das der Begriff der Titration auch in anderen Zusammenhängen auftreten kann. Hier ein kurzer Überblick über weitere mögliche Titrationstypen:

Redox-Titration
Komplexometrie
Thermometrische Titration

Neben dem Begriff der Titration wird analog auch von Volumetrie gesprochen. Im nächsten Schritt wollen wir uns um den experimentellen Aufbau und Ablauf einer Titration im allgemeinen kümmern.

Experimenteller Aufbau

#
Abb. 1: Darstellung einer Titrationsapparatur

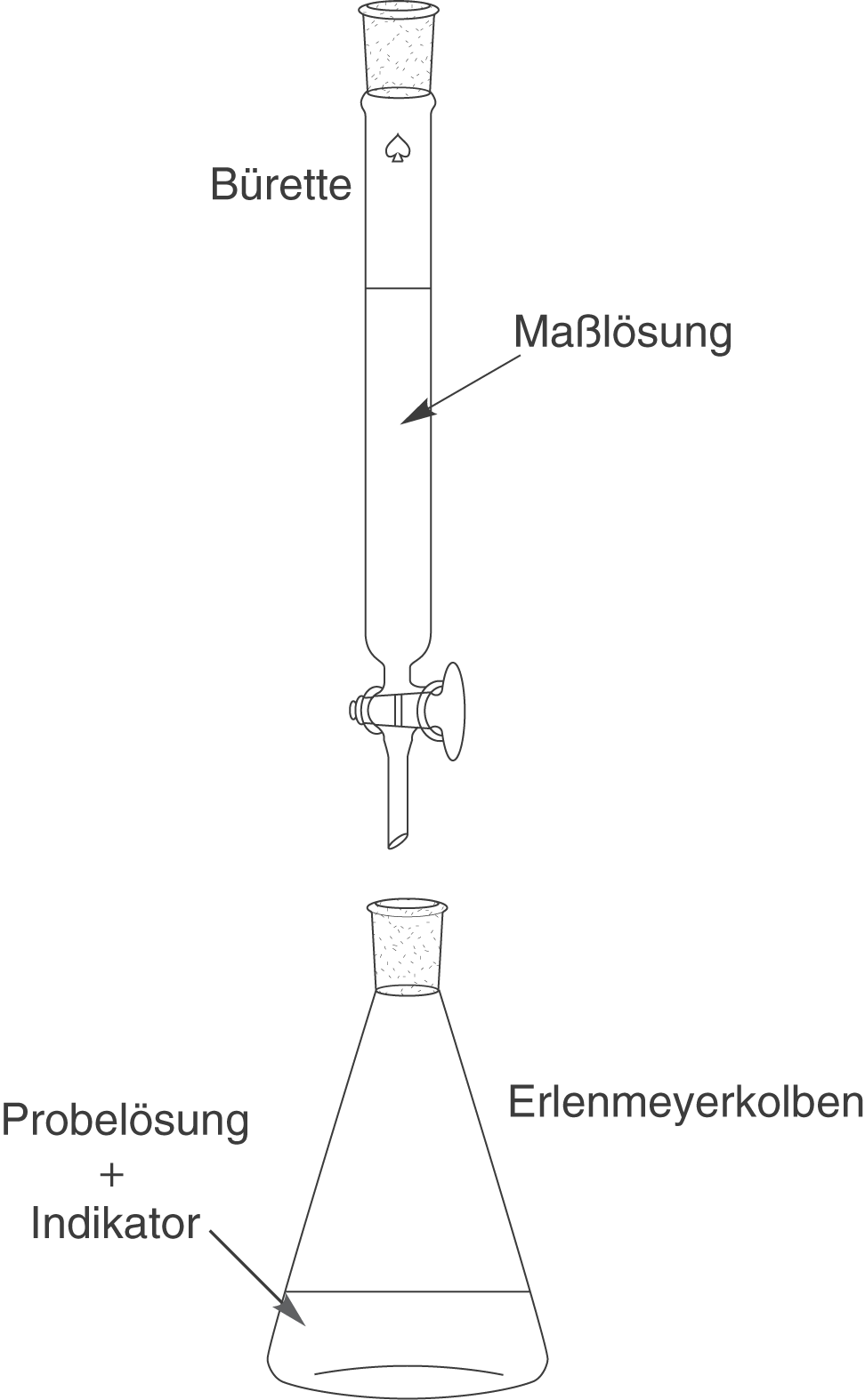
Der experimentelle Aufbau einer Titration besteht aus den folgenden zwei Komponenten:

Bürette mit Maßlösung
Erlenmeyerkolben mit Probelösung und Indikator

Natürlich kann sich die Probelösung auch in einem anderen Gefäß befinden, der Erlenmeyerkolben hat sich jedoch bewährt, da während der Titration ein leichtes Schwenken möglich ist, ohne, dass etwas von der Probelösung heraustropft und so das Messergebnis verfälscht. Auf der rechten Seite kannst du den oben beschriebenen experimentellen Aufbau einer Titration sehen. Wir wollen nun das Konzept an sich betrachten.
In der Bürette liegt eine Lösung bekannter Konzentration mit einem ebenfalls bekannten Volumen vor. Im Erlenmeyerkolben legen wir ein bekanntes Volumen an Probelösung vor und tropfen ein paar Tropfen eines geeigneten Indikators hinzu. Wir werden im Verlauf der Titration nun langsam die Maßlösung zur Probelösung hinzutropfen. Damit wird sich der pH-Wert der Probelösung ändern und der Indikator erreicht seinen Umschlagpunkt. An diesem Punkt ist dann auch der Äquivalenzpunkt der Titration erreicht. Hier liegen Säure und Base in der gleichen Konzentration vor.
Das Volumen an Maßlösung, welches verbraucht wurde wird nun für die Berechnung der unbekannten Konzentration der Probelösung benötigt.

Theorie und Stöchiometrie

Wir wollen uns in diesem Kapitel nun einmal genauer anschauen, welche Prozesse formal bei einer Säure-Base-Titration ablaufen und wie wir mit Hilfe der Stöchiometrie letzten Endes die unbekannte Konzentration unserer Probelösung berechnen können. Dazu nehmen wir ein Standardbeispiel: wir titrieren eine wässrige Lösung von HCl (Salzsäure) mit einer ein molaren ( $c(\text{NaOH}_{(\text{aq})}=1\,\frac{\text{mol}}{\ell})$ Natronlauge (NaOH $_{(\text{aq})}$ ). Die Salzsäure ist in diesem Fall unsere Probelösung und die Natronlauge unsere Maßlösung. Als Indikator verwenden wir ein paar Tropfen Phenolrot mit einem Umschlagsbereich von pH 6,4 - 8,2. Da Indikatoren bei Säure-Base-Titrationen selbst als schwache Säuren bzw. Basen wirken, muss darauf geachtet werden, dass nicht zuviel Indikator hinzugegeben wird. Ansonsten würde dieser mit titriert werden, was ebenfalls das Ergebnis verfälscht.
Bei der Titration läuft dann formal folgende Neutralisationsreaktion ab:

$\text{HCl}_{(\text{aq})}+\text{NaOH}_{(\text{aq})}$ $\rightleftharpoons$ $\text{NaCl}_{(\text{aq})}+\text{H}_{2}\text{O}_{(\ell)}$

In diesem Fall haben wir folglich eine saure Probelösung, die durch die Zugabe der Maßlösung nach und nach weniger sauer wird: der pH-Wert steigt. Wir splitten diese Reaktionsgleichung nun noch ein wenig weiter auf, damit wir den relevanten Prozess der Protolyse direkt sehen können. Salzsäure ist eine starke Säure, dass heißt sie dissoziiert in Wasser nahezu vollständig in Chlorid-Anionen und Oxoniumionen. Natronlauge ist hingegen eine starke Base. Damit liegen in der Maßlösung insbesondere freie Hydroxid-Ionen vor. Die Protolyse erfolgt dann wie du bereits gesehen hast:

$\text{Cl}_{(\text{aq})}^{-}+\text{H}_{3}\text{O}^{+}+\text{Na}_{(\text{aq})}^{+}+\text{OH}^{-}$ $\rightleftharpoons$ $2\;\text{H}_{2}\text{O}_{(\ell)}+\text{Na}_{(\text{aq})}^{+}+\text{Cl}_{(\text{aq})}^{-}$

Wir können außerdem sehen, dass laut der Reaktionsgleichung auf jedes Mol Salzsäure auch ein Mol Natronlauge kommt. Das heißt, dass zur Neutralisation eines Teils Salzsäure genau ein Teil Natronlauge benötigt wird. Wenn wir nun soviel Natronlauge zur Probelösung hinzugegeben haben, dass die beiden im gleichen Verhältnis vorliegen, dann können wir über das verbrauchte Volumen an Maßlösung berechnen, welche Konzentration die Salzsäure hatte. Zur Berechnung der unbekannten Konzentration der Salzsäure benötigen wir im Grund nur den folgenden Zusammenhang: $c=\dfrac{n}{V}$ . In Worten: die Stoffmengenkonzentration ist gleich dem Quotienten aus Stoffmenge und Volumen.
Nun stellen wir das Stoffmengenverhältnis für die betrachtete Reaktion auf:

$\dfrac{n(\text{HCl}_{(\text{aq})})}{n(\text{NaOH}_{(\text{aq})})}$ = $\dfrac{1}{1}$

Wenn wir die Formel für die Stoffmengenkonzentration nach der Stoffmenge umstellen und einsetzen erhalten wir:

$\dfrac{c(\text{HCl}_{(\text{aq})})\cdot V(\text{HCl}_{(\text{aq})})}{c(\text{NaOH}_{(\text{aq})})\cdot V(\text{NaOH}_{(\text{aq})})}$ = $\dfrac{1}{1}$

Folgende Größen in dieser Gleichung sind uns bereits bekannt:

$V(\text{HCl}_{(\text{aq})})$ : Volumen der vorgelegten Probelösung.
$V(\text{NaOH}_{(\text{aq})})$ : verbrauchtes Volumen der Maßlösung bis zum Umschlag des Indikators.
$c(\text{NaOH}_{(\text{aq})})$ : Konzentration der Maßlösung.

Damit ist die einzige Unbekannte $c(\text{HCl}_{(\text{aq})})$ . Nach dem Umformen erhalten wir:

$c(\text{HCl}_{(\text{aq})})$ = $\dfrac{V(\text{NaOH}_{(\text{aq})})\cdot c(\text{NaOH}_{(\text{aq})})}{V(\text{HCl}_{(\text{aq})})}$

Nach diesem Schema kannst du immer vorgehen, wenn du bei einer Titration die unbekannte Konzentration der Probelösung berechnen musst. Bevor wir uns im nächsten Kapitel insbesondere auch mit Titrationskurven auseinandersetzen, wollen wir uns nun noch zwei wichtige Begriff anschauen, bei denen es wichtig ist sie unterscheiden zu können.

(a) Neutralpunkt

Der Neutralpunkt entspricht einem pH-Wert von pH 7. An diesem Punkt ist die Lösung neutral. Wenn wir dazu die Definiton des pH-Werts heranziehen bedeutet das auch, dass die Konzentration der Oxoniumionen an diesem Punkt mit $c(\text{H}_{3}\text{O}^{+})=10^{-7}\,\frac{\text{mol}}{\ell}$ ist.

(b) Äquivalenzpunkt

Am Äquivalenzpunkt gilt:

$c(\text{H}_{3}\text{O}^{+})$ = $c(\text{OH}^{-})$

Hier ist die Konzentration der Oxoniumionen genauso groß, wie die Konzentration der Hydroxidionen. Der große Unterschied zum Neutralpunkt ist der, dass dieser Zustand auch schon bei sehr geringen oder erst bei sehr hohen Oxoniumionen-Konzentrationen erreicht wird. Und diese wirken sich dann direkt auf den pH-Wert aus. Nur in Ausnahmefällen fallen Äquivalenzpunkt und Neutralpunkt auf den gleichen pH-Wert!

Säure-Base-Titration

Wir wollen uns nun verschiedene Säure-Base Titrationen anschauen und den Titrationsverlauf mithilfe von Titrationskurven erklären lernen. Ganz allgemein ist im Falle einer Titrationskurve das zugegebene Volumen der Maßlösung auf der x-Achse und der pH-Wert der Probelösung auf der y-Achse aufgetragen.

Starke Säuren und starke Basen

In diesem Kapitel beschäftigen wir uns mit der Titration von starken Säuren mit starken Basen und umgekehrt. Das Prinzip ist beides mal das gleiche, nur die Titrationskurven unterscheiden sich voneinander. Damit dieser Unterschied deutlich wird, wollen wir beiden Varianten getrennt betrachten.

Titration einer starken Säure mit einer starken Base

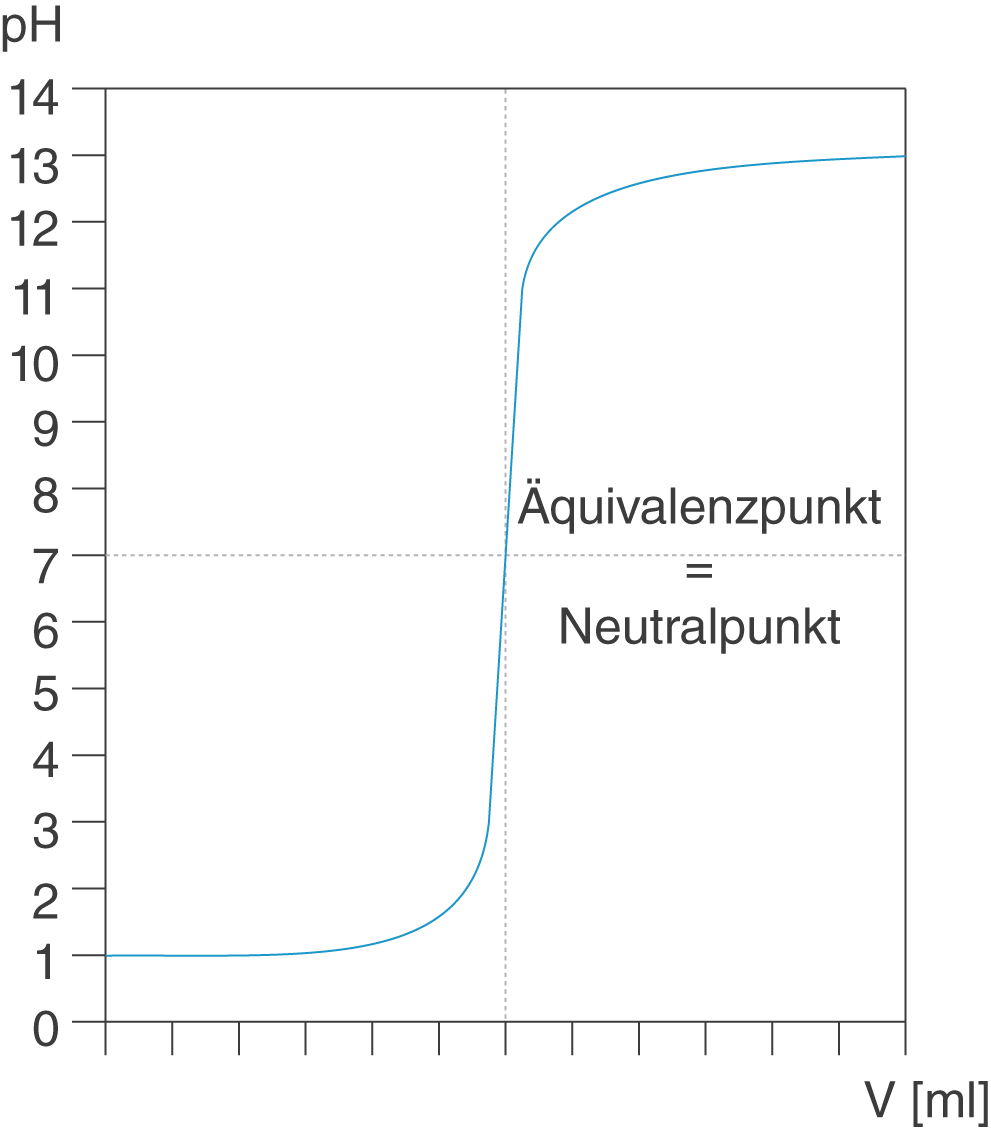
Dieser Verlauf ist charakteristisch für die Titration einer starken Säure mit einer starken Base. Zu Beginn hat die Probelösung einen pH-Wert im sauren Bereich. Durch die Zugabe der alkalischen Maßlösung nimmt der pH-Wert zu. In diesem Fall fallen Äquivalenzpunkt und Neutralpunkt genau auf pH 7.

Du kannst sehen, dass im Bereich des Umschlagspunkts bereits minimale Mengen an Maßlösung ausreichen, damit der pH-Wert um mehrere Einheiten nach oben springt. Dieses Verhalten stellt oft die Schwierigkeit bei der Titration dar: In diesem Bereich muss extrem vorsichtig gearbeitet werden. Titrierst du zum Beispiel Salzsäure mit Natronlauge unter Verwendung des Indikators Phenolphtalein, so ist deine Lösung lange Zeit farblos. Näherst du dich dem Äquivalenzpunkt, so gibst du nur noch sehr langsam Natronlauge zu. Machst du dies nicht, so wird deine Lösung schlagartig pink und du hast zu weit titriert. Dann heißt es, das ganze Experiment zu wiederholen.

Abb. 2: Titrationskurve bei Titration einer starken Säure mit einer starken Base

Titration einer starken Base mit einer starken Säure

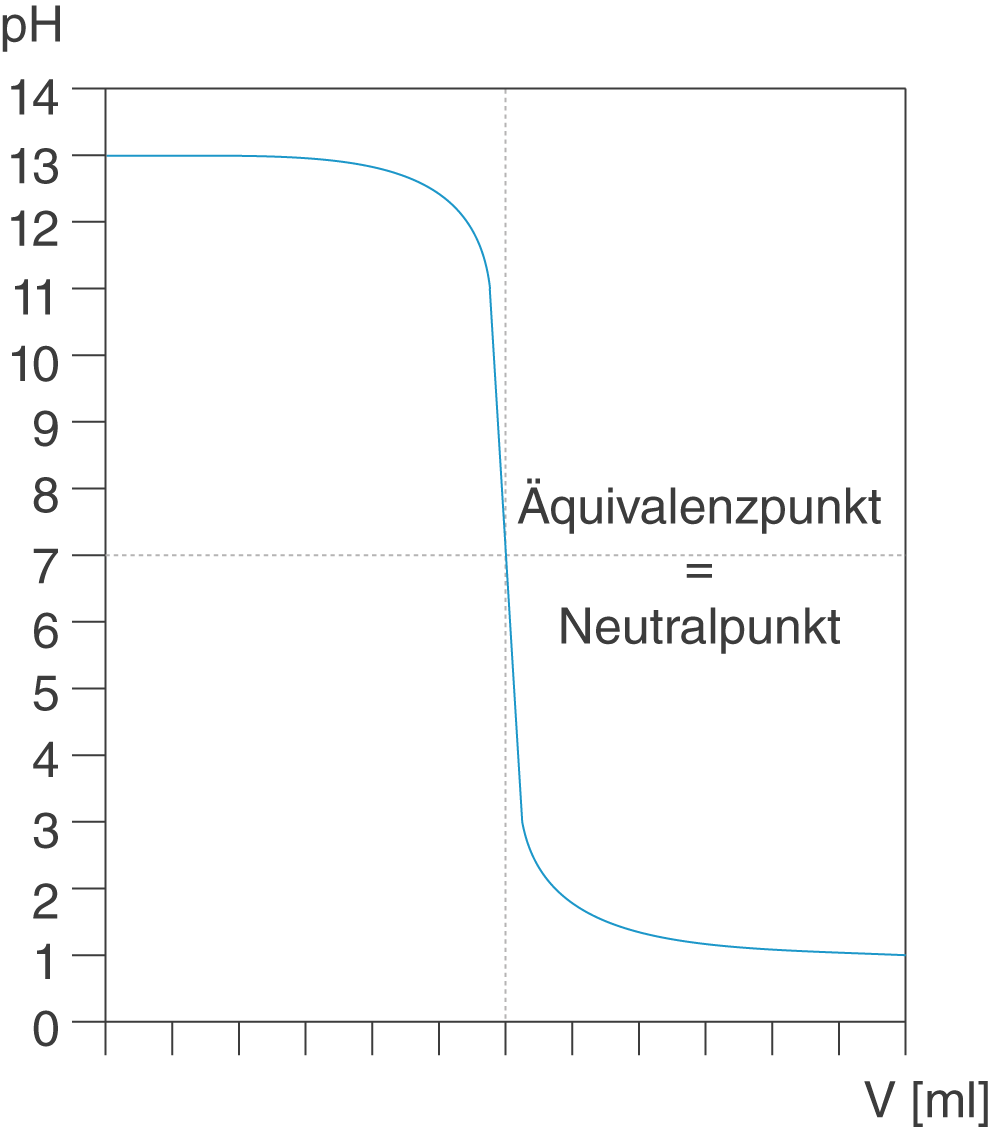
Diese Titrationskurve sieht ganz ähnlich aus, wie die bereits besprochenen. Der große Unterschied ist, dass wir hier eine starke Base als Probelösung vorliegen haben. Damit ist der pH-Wert zu Beginn der Titration auch sehr alkalisch. Durch die Zugabe von Säure in Form der Maßlösung nimmt der pH-Wert ab. Auch hier entspricht der Äquivalenzpunkt dem Neutralpunkt.

Abb. 3: Titrationskurve bei der Titration einer starken Base mit einer starken Säure

Ungleiche Säure- und Basenstärken

Bei der Titration von schwachen Säuren mit starken Basen und von schwachen Basen mit starken Säuren treten ein paar Besonderheiten auf. Aus diesem Grund schauen wir uns diese getrennt an.

Titration einer schwachen Säure mit einer starken Base

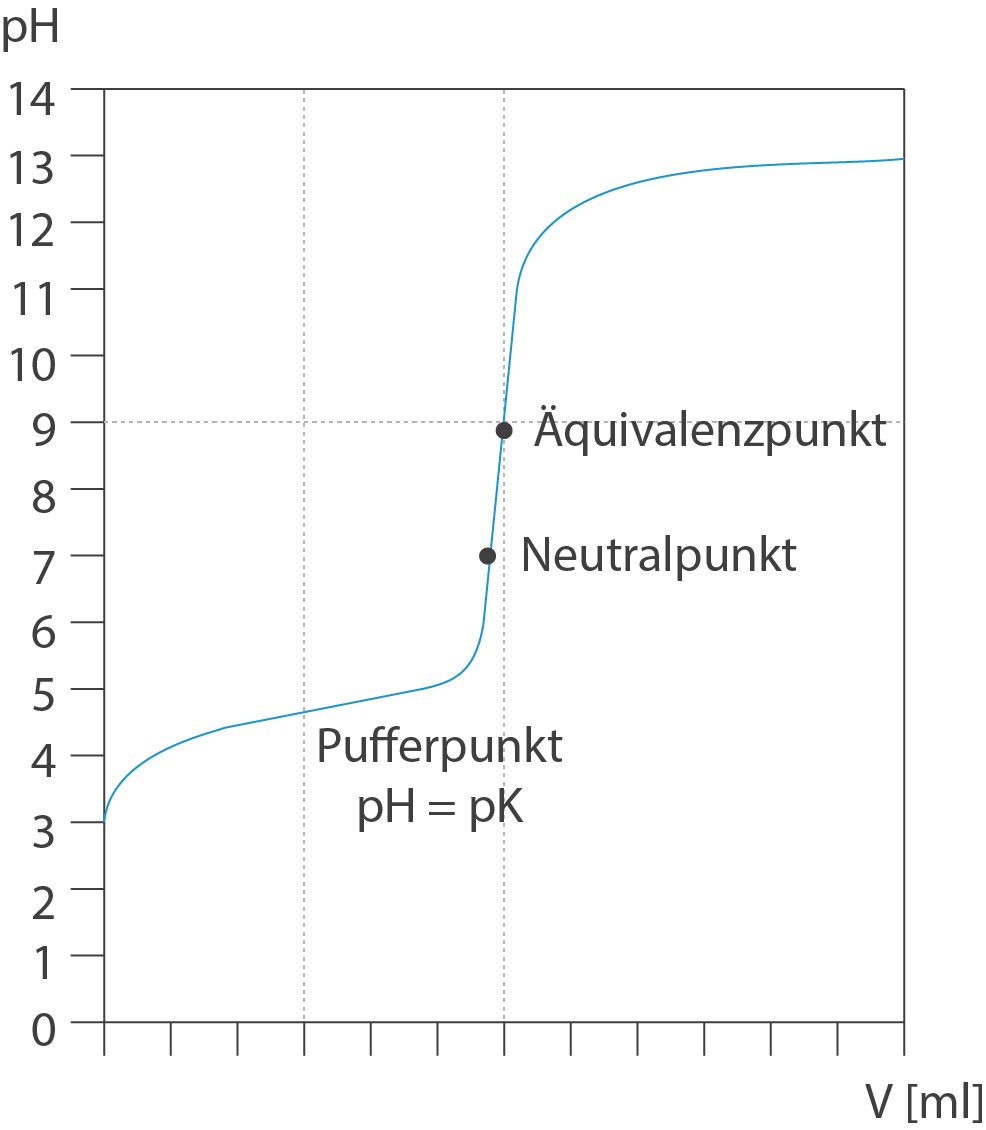
Bei der Titration einer schwachen Säure entsteht das korrespondierende Säureanion. Bei geeigneten Mischungsanteilen von Säure und korrespondierendem Säureanion liegt eine Pufferlösung vor. Der Pufferpunkt liegt am ersten Wendepunkt der Titrationskurve mit pH = $\text{pK}_{\text{S}}$ . Am Äquivalenzpunkt ist die gesamte Säure neutralisiert. Der pH-Wert am Äquivalenzpunkt wird von der korrespondierenden Base der schwachen Säure, dem Säureanion, bestimmt. Hier kannst du auf dein Wissen bzgl. der Beeinflussung des pH-Werts durch Salze zurückgreifen: Salze schwacher Säuren reagieren basisch, weil das Säureanion eine stärkere Base ist. Der Äquivalenzpunkt fällt folglich nicht mit dem Neutralpunkt zusammen, denn neutral ist die Lösung bereits bei pH 7, doch hier ist noch nicht die ganze Säure neutralisiert.

Abb. 4: Titrationskurve bei der Titration einer schwachen Säure mit einer starken Base

Titration einer schwachen Base mit einer starken Säure

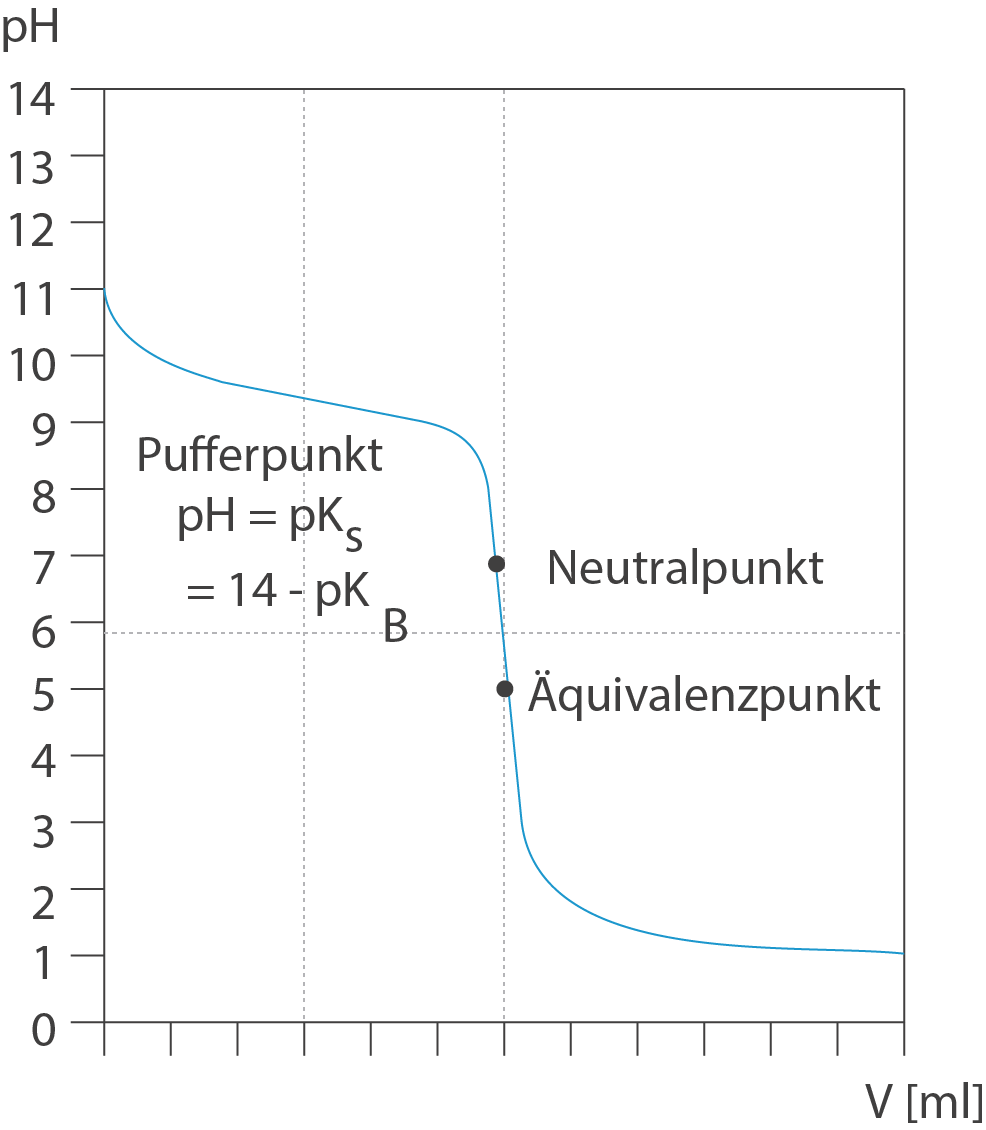
Bei der Titration einer schwachen Base läuft die Titration vergleichbar ab, wie im Fall der schwachen Säure. Hierbei wird die Base nach und nach protoniert, bis sich eine Mischung aus schwacher Säure und korrespondierender Base einstellt. Der Pufferpunkt wird bei $\text{pH}=\text{pK}_{\text{S}}=14-\text{pK}_{\text{B}}$ erreicht und liegt im basischen Bereich. Ist die gesamte Base neutralisiert, dann liegt nur noch die korrespondierende Säure vor, welche den pH-Wert am Äquivalenzpunkt in den sauren pH-Bereich verschiebt. Wieder sind der &AUml;quivalenzpunkt und der Neutralpunkt nicht am selben pH-Wert zu finden.

In jedem Fall ist es notwendig, dass die charakteristischen pH-Werte wie Pufferpunkt, Äquivalenzpunkt und Neutralpunkt gut bestimmt werden können. Dabei kannst du auch so vorgehen, dass du mithilfe eines Lineals den Graphen auswertest. Das hört sich zwar zunächst sehr unwissenschaftlich und ungenau an, ist jedoch für den ersten Eindruck sehr hilfreich und weist in diesem Zusammenhang auch eine genögend hohe Genauigkeit auf. Somit kannst du beispielsweise die verschiedenen Volumina an Maßlösung bestimmen, die nötig sind, um die pH-Werte der oben angesprochenen Punkte zu erreichen. Dazu suchst du die Schnittstelle einer Senkrechten mit der x-Achse, die durch diesen besagten Punkt verläuft.

Abb. 5: Titrationskurve bei der Titration einer schwachen Base mit einer starken Säure

Bildnachweise [nach oben]

[1]

Public Domain.

[2]

[3]

[4]

[5]