Monosaccharide
Definition
Monosaccharide (Einfachzucker) stellen die Bausteine für eine der wichtigen Naturstoffklassen dar: die Kohlenhydrate. Wir werden in diesem Skript auf dir bereits bekannte Verbindungen wie Traubenzucker (Glucose) und Fruchtzucker (Fructose) zu sprechen kommen und deren Chemie betrachten.


Wir werden dieses Skript mit der Fischer-Projektion beginnen, die es uns erlaubt, Monosaccharide auf eine geeignete Art und Weise darzustellen. Im Anschluss wenden wir uns den Monosacchariden am Beispiel von Glucose und Fructose zu. Wir betrachten deren Molekülaufbau und dessen Auswirkung auf die optische Aktivität der Moleküle. Im nächsten Schritt schauen wir uns cyclische Monosaccharide und die Haworth-Projektion an. Hier beginnen wir damit, die Fischer-Projektion in die Haworth-Projektion zu überführen (Ringschluss), lernen dann den Begriff des Anomers kennen und betrachten abschließend die Chemie des Ringschlusses. Daraufhin wenden wir uns zwei Phänomenen zu, die wir bei Glucose und Fructose in wässrigen Lösungen beobachten können: der Mutarotation von Glucose sowie der Keto-Enol-Tautomerie. Wir schließen das Skript Monosaccharide mit dem Nachweis von reduzierenden Zuckern ab.
Die Fischer-Projektion
Grundlagen der Fischer-Projektion
geeigneten Darstellungsweise für organische Moleküle ist die Fischer-Projektion. Diese geht auf den Nobelpreisträger für Chemie, Emil Fischer, aus dem Jahr 1902 zurück. Organische Moleküle sind dreidimensionale Strukturen, die wir unter Verwendung der Keil-Strich-Schreibweise (vgl. ChemieLV-Skript Stereoisomerie und optische Aktivität) entsprechend darstellen können. Die Fischer-Projektion ermöglicht uns, die dreidimensionale Struktur von Moleküle in eine zweidimensionale Darstellung zu überführen (vgl. Abb. 2).
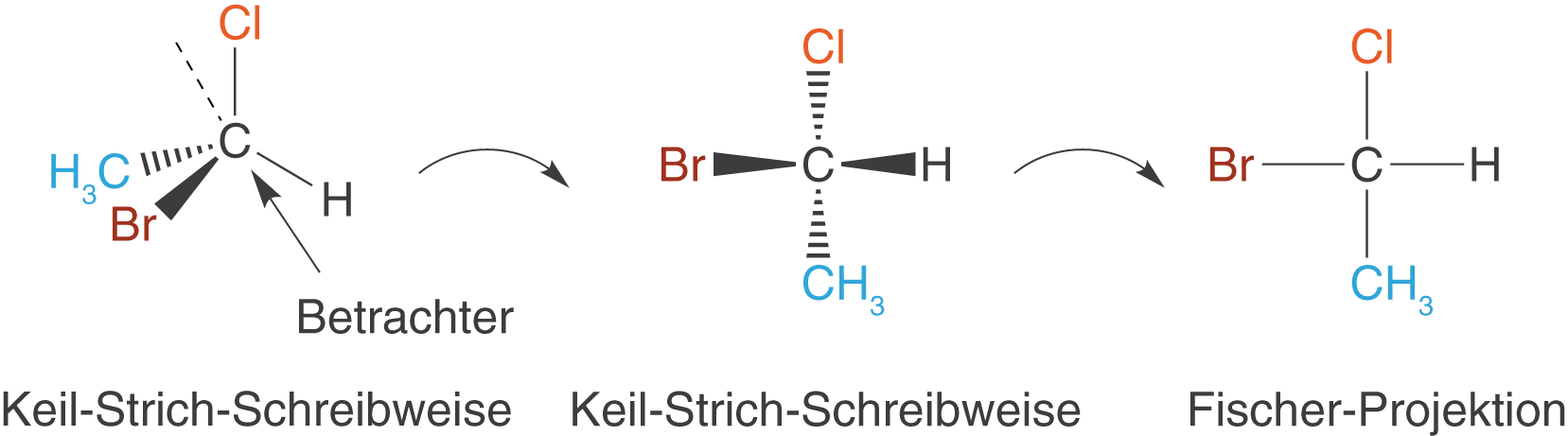
Wir gehen hier folgendermaßen vor:
- Wir schauen als Betrachter von schräg unten auf das C-Atom, sodass das rot eingefärbte Br-Atom links und das schwarz eingefärbte H-Atom rechts vom Betrachter steht.
- Aus Schritt 1 ergibt sich die Ansicht in diesem Schritt: Das H- und das Br-Atom auf der waagrechten Achse zeigen aus der Zeichenebene heraus auf uns zu, während das Cl-Atom und der Methylrest (
) auf der senkrechten Achse hinter die Zeichenebene zeigen.
- Wenn wir dieses Molekül nun gedanklich „platt“ drücken, dann liegen alle Bindungen in einer Ebene und wir erhalten die Fischer-Projektion.
Es gibt nicht nur eine richtige Darstellung der Keil-Strich-Schreibweise, was die Substituenten angeht. Folglich gibt es unter Voraussetzung der Stellung unter Schritt 2 auch mehrere korrekte Darstellungen der Fischer-Projektion für ein Molekül.
Wir ändern die Blickrichtung des Betrachters und beachten die Vorgaben bei der Projektion:
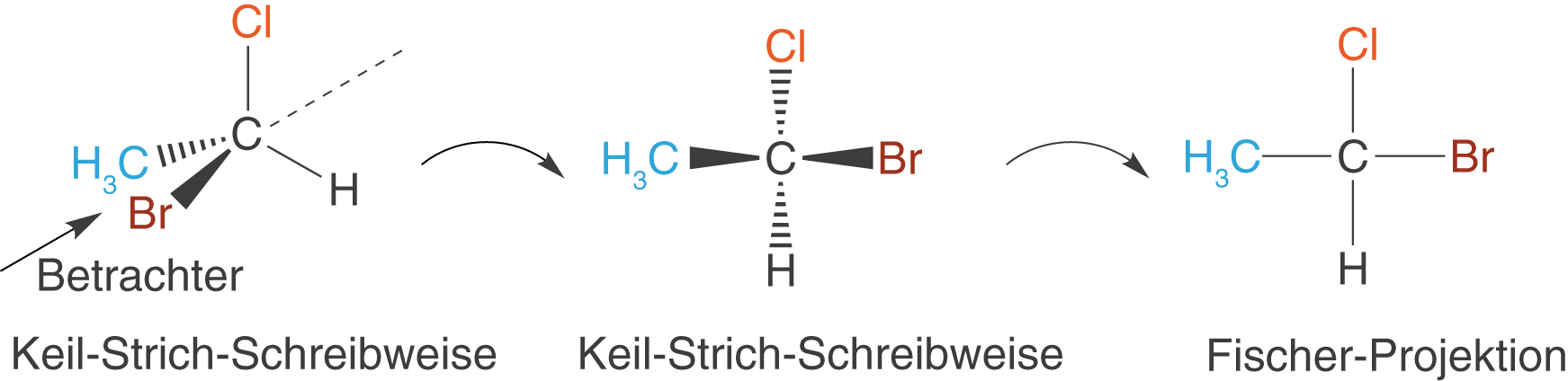
Du kannst dir auch merken, dass bei der Fischer-Projektion alle Substituenten (Reste) in derselben Ebene wie das jeweilige asymmetrische Kohlenstoffatom liegen (vgl. ChemieLV-Skript Stereoisomerie und optische Aktivität). Wir verwenden die Fischer-Projektion insbesondere im Zusammenhang mit chiralen Verbindungen, um die Stellung der Substituenten am asymmetrischen C-Atom zu bestimmen.
Wir wollen uns nun damit beschäftigen, wie verschiedene Symmetrieoperationen (vor allem Drehungen) die Fischer-Projektion verändern. Dieser Aspekt ist wichtig, wenn wir die offenkettige Form von Zuckern von der Fischer-Projektion in die cyclische Form der Haworth-Projektion überführen wollen (s.u.).
Symmetrieoperationen in der Fischer-Projektion
Bei der Veränderung der Fischer-Projektion eines Moleküls müssen wir aufpassen, dass wir nicht die eigentliche Struktur des Moleküls verändern. Das hängt damit zusammen, dass die Fischer-Projektion dreidimensionale Objekte in zwei Dimensionen abbildet.
Gehe bei einer Veränderung der Substituentenstellung immer so vor, dass du die Fischer-Projektion zunächst wieder in die Keil-Strich-Schreibweise überführst, die Symmetrieoperation (bspw. Drehen) durchführst und die neue Darstellung wieder in der Fischer-Projektion schreibst.
Drehung um 
Wir können Moleküle in der Fischer-Projektion um drehen, ohne dass sich die Orientierung der Substituenten verändert (vgl. Abb. 4). Die Drehachse kommt hierbei auf dich zu und verläuft durch das C-Atom.

Drehung um eine Bindungsachse
Wir nehmen das Molekül aus dem letzten Beispiel und führen eine Drehung um die Bindungsachse durch, die durch das Cl- und das C-Atom verläuft.
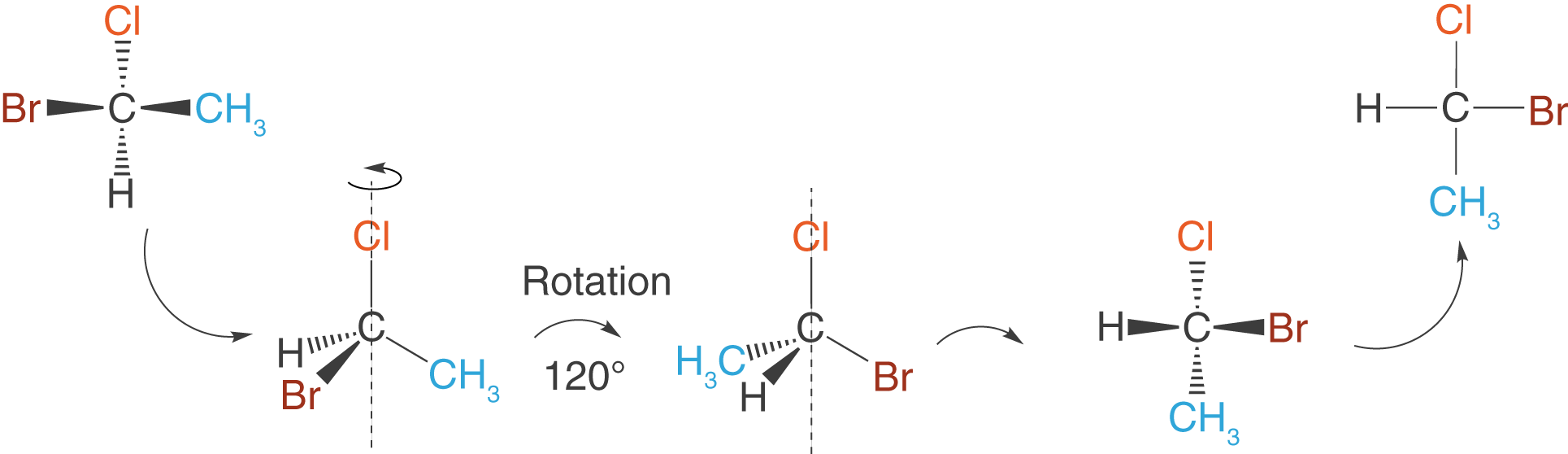
Du kannst sehen, dass sich die Position des Cl-Atoms nicht verändert hat, während die anderen Substituenten dem Schema in Abbildung 6 folgen:
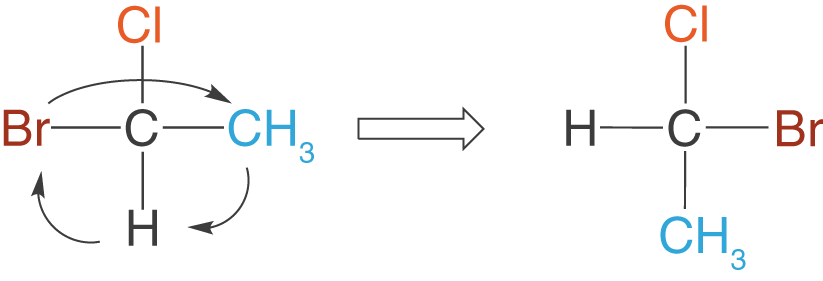
Die Drehung um die -Bindungsachse kannst du auch dann erreichen, wenn du in der Fischer-Projektion die Stellung des Cl-Atoms festhältst und die restlichen Substituenten im Uhrzeigersinn um das Kohlenstoffatom rotieren lässt.
Monosaccharide: Begriffsbildung und Eigenschaften
Glucose und Fructose
Darstellung in der Fischer-Projektion
Monosaccharide sind die kleinsten Baueinheiten der Kohlenhydrate: deren Monomere. Zu den bekanntesten Monosacchariden (Einfachzuckern) zählen die Glucose (Traubenzucker) und die Fructose (Fruchtzucker). Bei der Darstellung von Glucose und Fructose in der Fischer-Projektion gehen wir so vor, dass das höchstoxidierte C-Atom oben steht und sich die anderen C-Atome auf einer Senkrechten darunter befinden (vgl. Abb. 7).
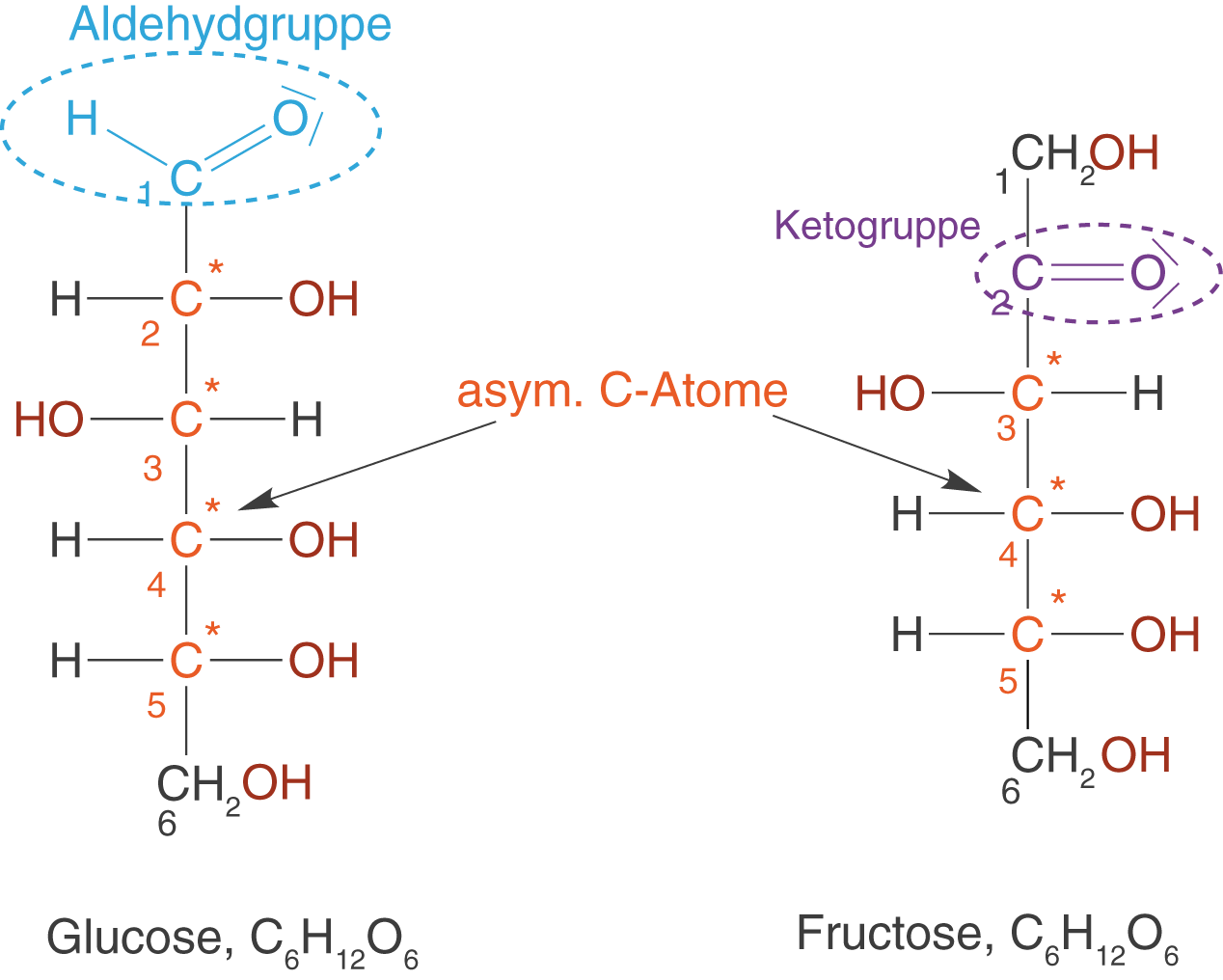
Hieran können wir folgende Eigenschaften erkennen:
- Glucose weist eine endständige Aldehydgruppe auf, weshalb sie zu den Aldosen zählt.
- Fructose weist eine Ketogruppe auf, weshalb sie zu den Ketosen zählt.
- Glucose und Fructose besitzen neben den schon angesprochenen funktionellen Gruppen mehrere OH-Gruppen. Durch das Auftreten vieler funktioneller Gruppen spricht man bei diesen Molekülen auch von Polyfunktionalität.
- Beide Monosaccharide sind aus einem Grundgerüst von sechs C-Atomen aufgebaut. Im Allgemeinen werden die Zucker nach der Länge dieses Grundgerüsts (der Anzahl der C-Atome) eingeteilt: Triosen (3 C-Atome), Tetrosen (4 C-Atome), Pentosen (5 C-Atome) und Hexosen (6 C-Atome). Glucose und Fructose zählen zu den Hexosen.
- Die allgemeine Summenformel für Zucker lautet
. Für die Hexosen erhalten wir mit
die entsprechende Summenformel
.
D- und L-Konfiguration
Du kannst erkennen, dass beispielsweise Glucose vier asymmetrische C-Atome aufweist. Des Weiteren ist es nicht möglich, eine Symmetrieebene innerhalb des Moleküls zu finden, geschweige denn ein Symmetriezentrum zu setzen. Glucose ist folglich ein chirales Molekül und optisch aktiv (vgl. ChemieLV-Skript Stereoisomerie und optische Aktivität). Die Enantiomere der Zucker, an dieser Stelle insbesondere der Glucose, werden nach folgendem Schema benannt:
- Das maßgebliche asymmetrische C-Atom ist das, welches am weitesten von der Aldehyd- bzw. Ketogruppe entfernt ist.
- Die Stellung der OH-Gruppe bestimmt den Charakter: nach rechts
D-Enantiomer; nach links
L-Enantiomer
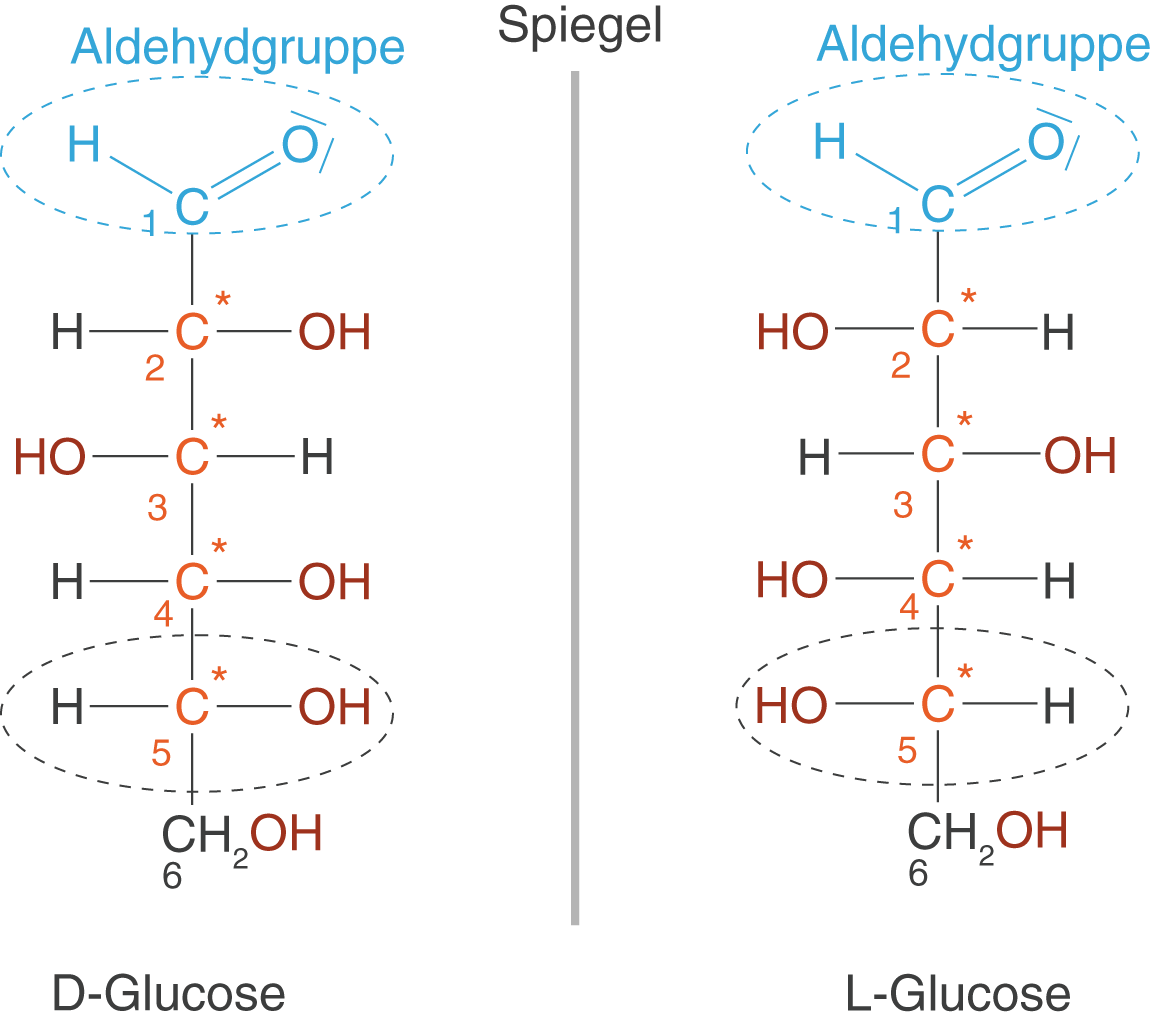
Die Bezeichnungen D und L sind für die Charakterisierung der Enantiomere wichtig; es besteht kein Zusammenhang zur optischen Aktivität der Enantiomere! Das bedeutet in keinem Fall, dass das D-Enantiomer immer rechtsdrehend wäre.
Cyclische Formen von Monosacchariden: Die Haworth-Projektion
Die Fischer-Projektion erlaubt uns eine zweidimensionale Darstellung dreidimensionaler Moleküle. Diese Darstellung entspricht nicht der Realität, wie wir sehen konnten, sondern leitet sich aus der Keil-Strich-Schreibweise ab. Eine andere Projektion für Monosaccharide, die die Molekülstruktur realistischer wiedergibt, geht auf den britischen Chemiker und Nobelpreisträger (1937) Sir Walter N. Haworth zurück: die Haworth-Projektion (vgl. Abb. 9).
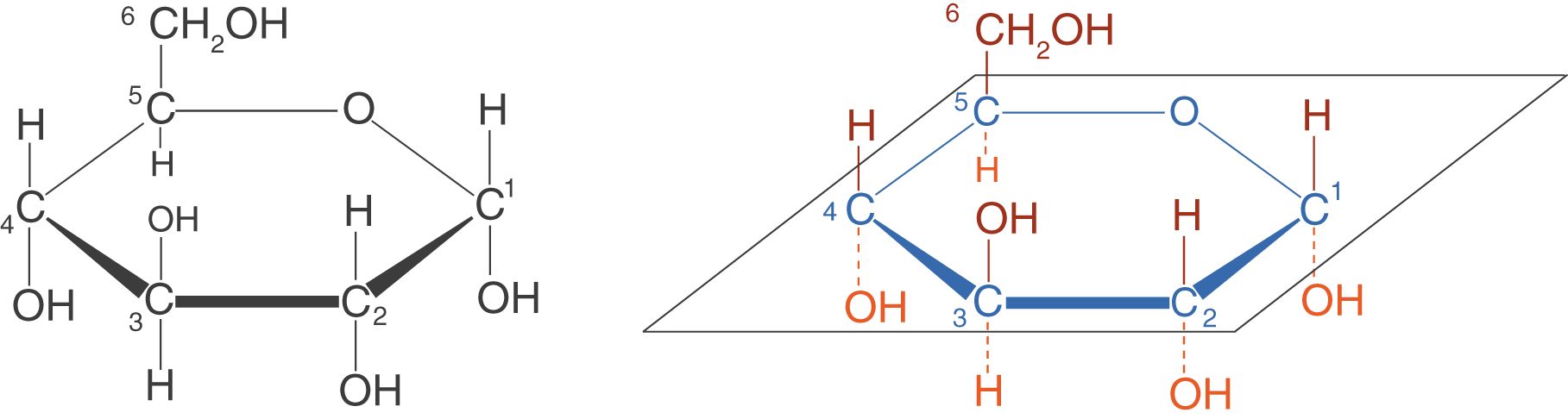
- Fett gezeichnete Bindungen kommen wie bei der Keil-Strich-Schreibweise auf den Betrachter zu.
- Alle blau eingezeichneten Bindungen und Atome liegen in derselben Ebene.
- Alle durchgezogenen roten Bindungen sowie die zugehörigen Substituenten befinden sich über der eingezeichneten Ebene.
- Alle gestrichelten orangefarbenen Bindungen sowie die zugehörigen Substituenten befinden sich unter der eingezeichneten Ebene.
- Wie kommen wir von der Fischer- zur Haworth-Projektion?
- Was sind
- und
-Anomere?
- Um welchen Bindungstyp handelt es sich, wenn es zum Ringschluss kommt?
Von der Fischer- zur Haworth-Projektion
Der Ringschluss
Wir können die Fischer-Projektion durch ein geeignetes Verfahren in die Haworth-Projektion überführen. Wir wollen hier nur die technischen Details dieses Vorgehens klären. Die chemische Begründung, also wie dieser Ringschluss überhaupt zu Stande kommen kann, klären wir unter 3.2.3.
Ein Aspekt ist in diesem Kapitel besonders wichtig: Wir müssen uns immer über die dreidimensionale Struktur des betrachteten Moleküls im klaren sein! Dies kann sich durch die verschiedenen Projektionen als schwierig herausstellen.
(a) D-Glucose in der Fischer-Projektion
Alle Substituenten, die in der Fischer Projektion zu den Seiten weg zeigen, zeigen in der Keil-Strich-Schreibweise auf den Betrachter zu. Die Stellung der OH-Gruppen im D-Glucosemolekül kannst du dir mit folgendem Merkspruch merken: „Ta-Tü-Ta-Ta“, wobei alle rechts stehenden Substituenten ein Ta und die links stehenden ein Tü zugeordnet bekommen.
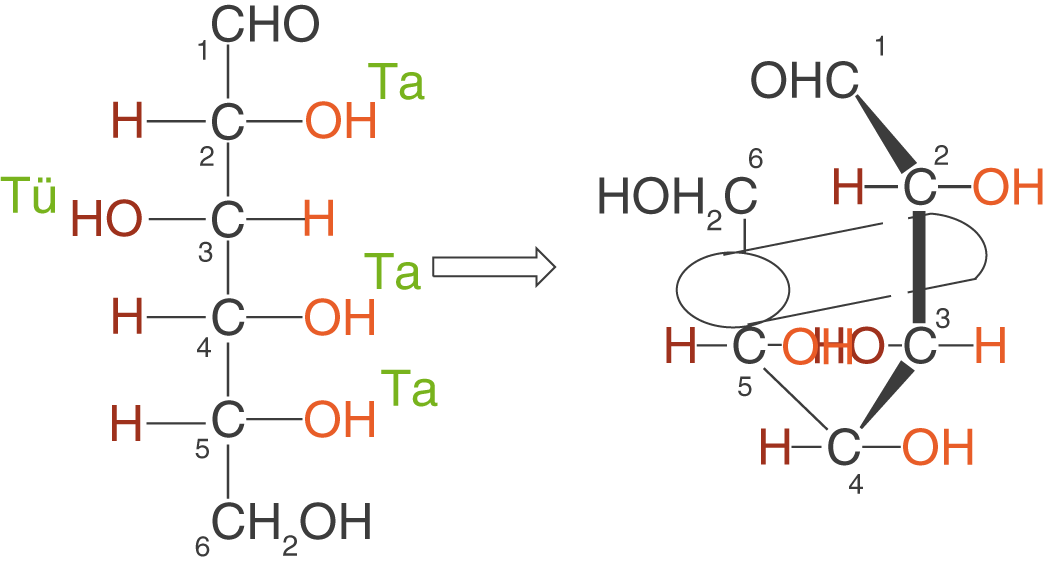
Wir „rollen“ das Molekül in der Fischer-Projektion quasi auf einer Rolle auf (vgl. Abb. 10).
(b) Waagrechte Darstellung der „aufgerollten“ Form
Nun kippen wir das so „aufgerollte“ Molekül um in die Waagrechte:
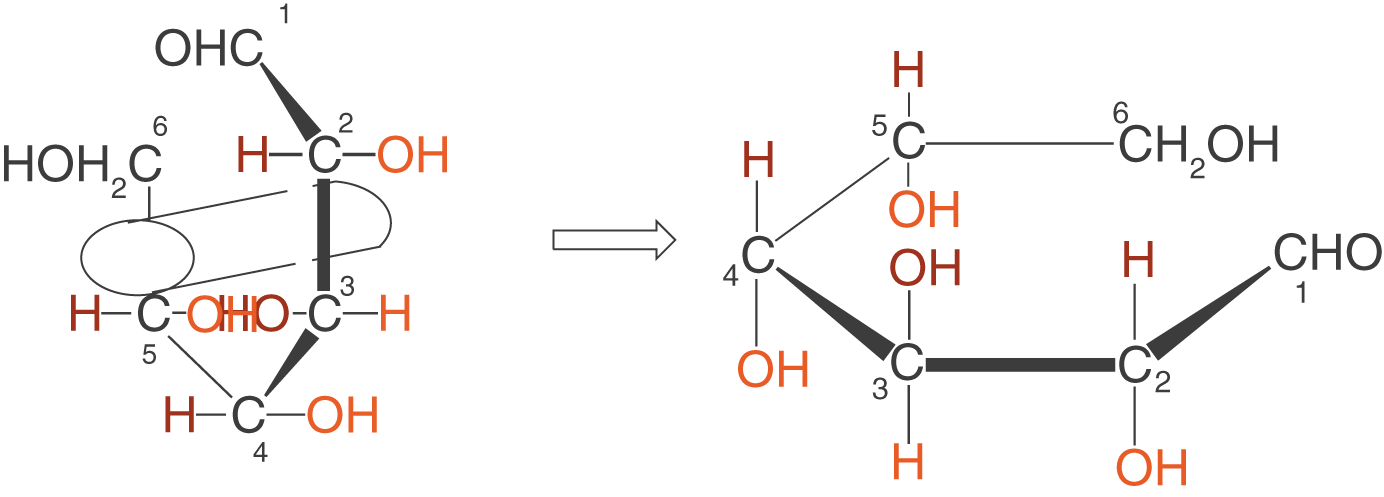
(c) Drehen des C-5-Atoms um
Wir drehen das C-5-Atom nun um die Bindungsachse, die durch dieses und das C-4-Atom verläuft. Somit liegt es in der gleichen Ebene, wie das C-1-Atom, was uns im letzten Schritt den Ringschluss erlaubt.
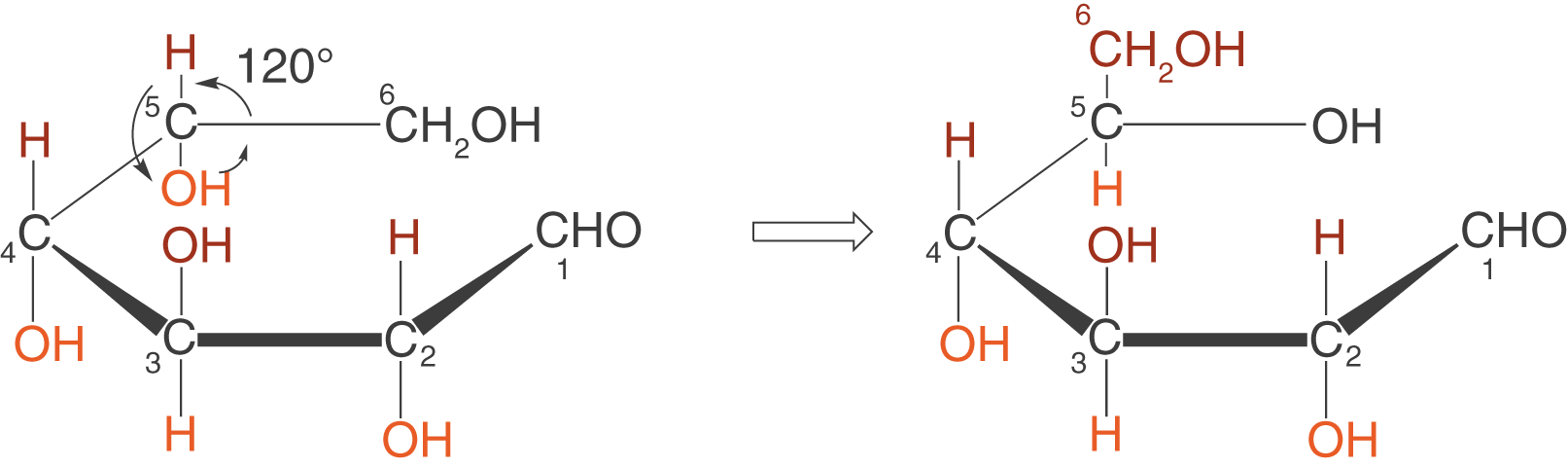
Bedenke hier unser Vorgehen unter 2.2.
(d) Ringschluss
Der Ringschluss findet am C-1-Atom statt. Das Wasserstoffatom der OH-Gruppe wird hierbei abgespalten.
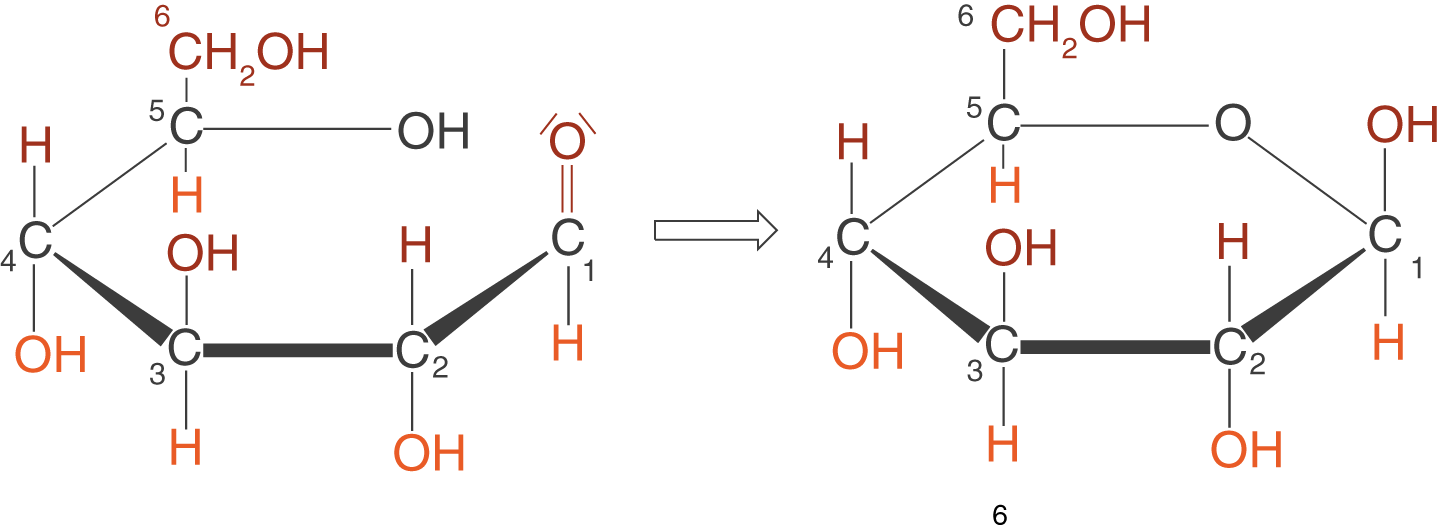
Pyranosen und Furanosen
Die in Abbildung 13 vorliegende sechseckige Struktur der D-Glucose wird auch D-Glucopyranose genannt, weil sie sich von dem zyklischen Ether Pyran ableitet. Wiederum befinden sich alle orange gefärbten Substituenten unter und alle rot gefärbten Substituenten über dem Ring. Der Ringschluss der L-Glucose funktioniert genauso.
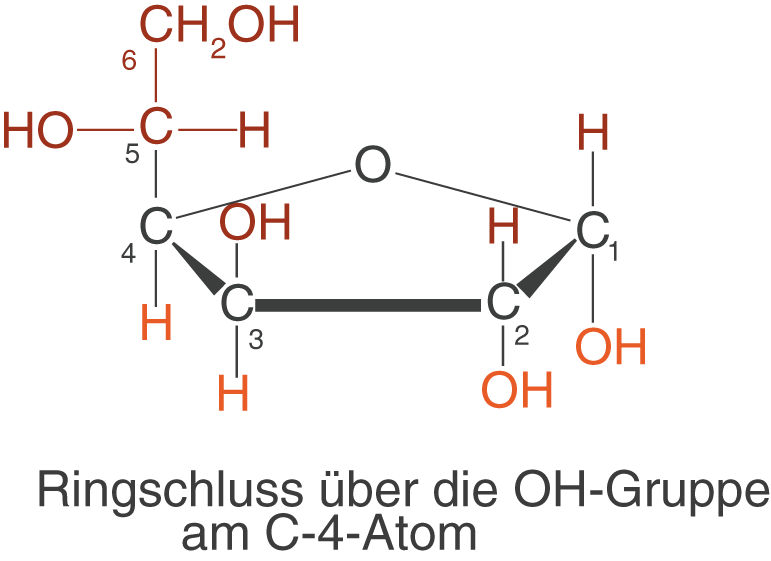
Neben den Pyranosen existieren auch fünfeckige Ringe: Die Furanosen, deren Namen sich vom zyklischen Ether Furan ableitet.
Im Fall der D-Glucofuranose findet der Ringschluss ebenfalls am C-1-Atom statt, jedoch mit dem Unterschied, dass die beteiligte OH-Gruppe vom C-4- statt vom C-5-Atom kommt. Diese Struktur ist energetisch gesehen instabiler als die der Pyranose - der Ring steht stärker unter Spannung.
Neben der D-Glucose können wir nun auch die D-Fructose in der Haworth-Projektion zeichnen (vgl. Abb. 14).
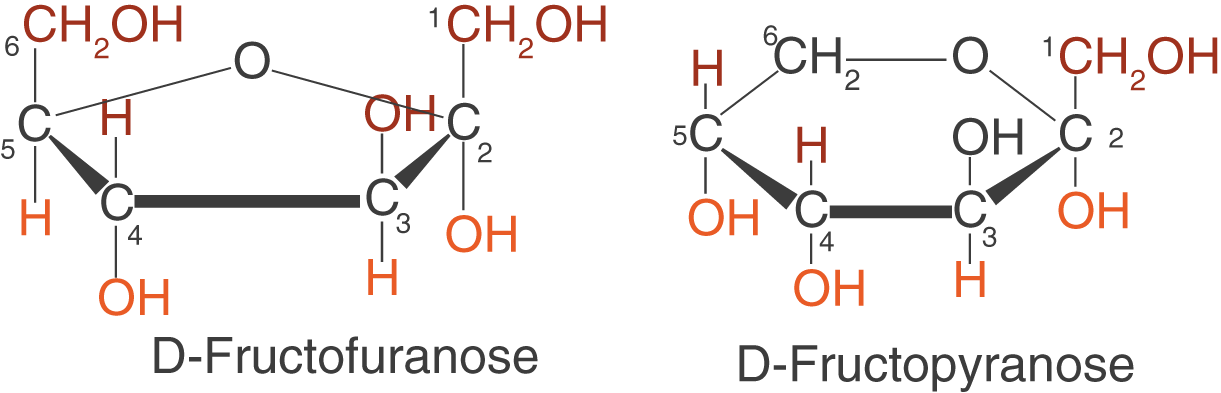
Der Ringschluss findet bei der D-Fructose am C-2-Atom statt, also an demjenigen, das Teil der Ketogruppe ist.
 - und
- und  -Anomere
-Anomere
Wir wollen uns an dieser Stelle das Kohlenstoffatom genauer anschauen, an welchem der Ringschluss stattfindet. Im Fall der D-Glucose handelt es sich um das C-1-Atom und im Fall der Fructose um das C-2-Atom (vgl. Abb. 13). Beispielhaft betrachten wir wieder die D-Glucose.
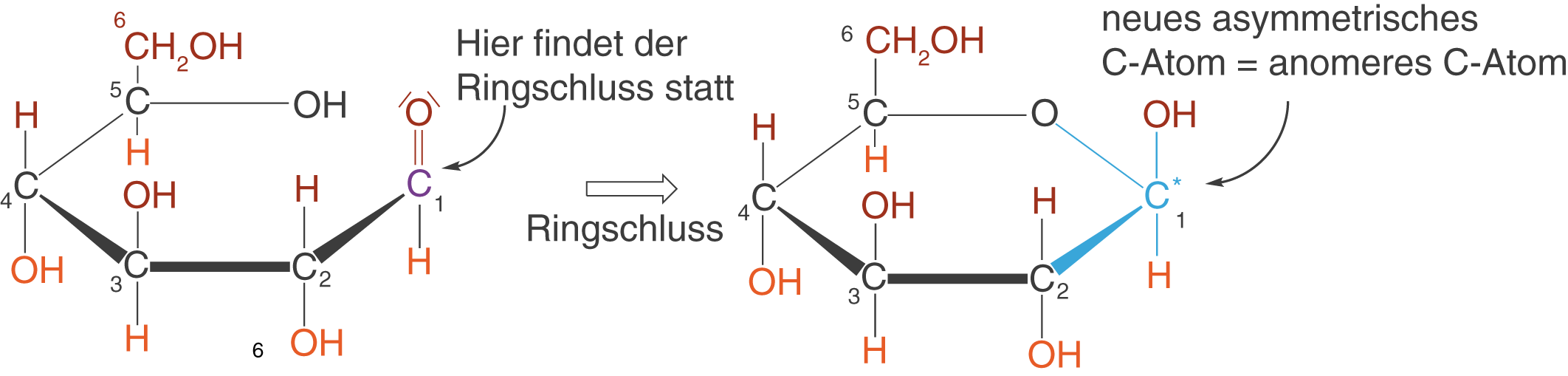
Beim Ringschluss bildet sich ein neues asymmetrisches C-Atom, nämlich das, an welchem er stattfindet (vgl. Abb. 15). Hierdurch werden zwei unterschiedliche Produkte beim Ringschluss möglich, die sich in der Stellung der Substituenten am C-1-Atom unterscheiden: die -D-Glucose und die
-D-Glucose. Das neue asymmetrische C-Atom wird anomeres C-Atom genannt.
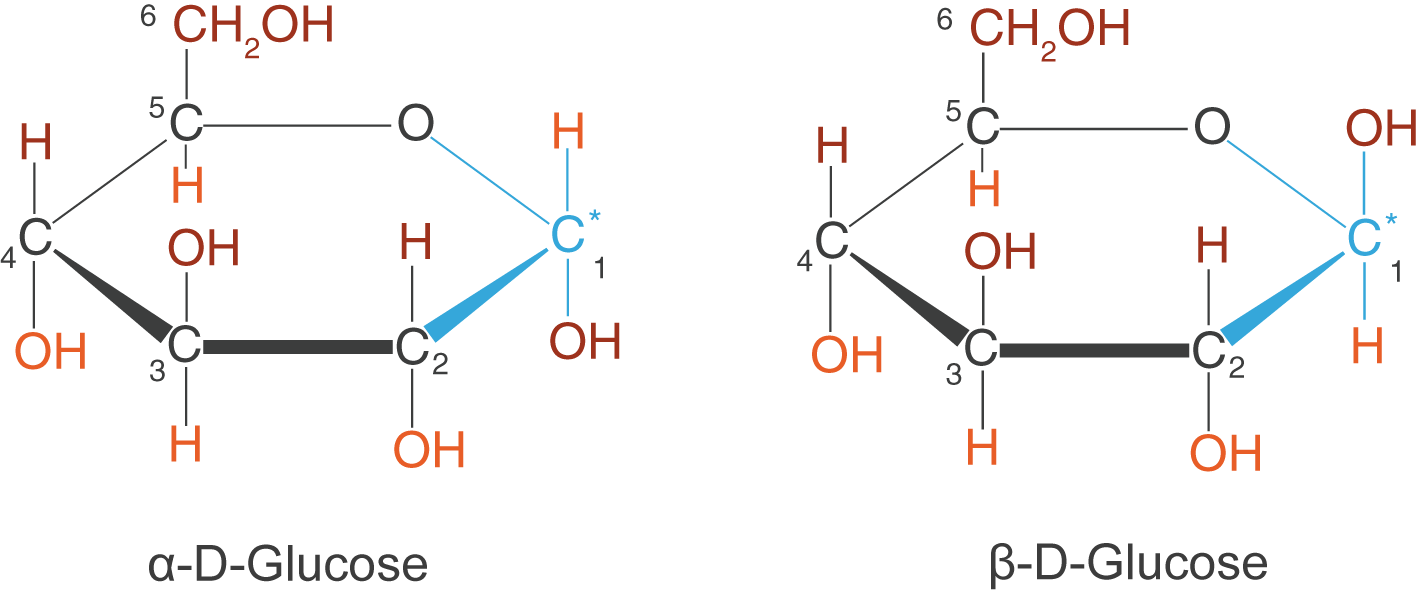
- Im Fall des
-Anomers befindet sich die OH-Gruppe am C-1-Atom unten.
- Im Fall des
-Anomers befindet sich die OH-Gruppe am C-1-Atom oben.
Halbacetale
In einem letzten Schritt wollen wir uns die Gruppe der Halbacetale anschauen, zu denen cyclische Monosaccharide zählen. Halbacetale können im Allgemeinen durch die Reaktion von Alkoholen mit Aldehyden oder Ketonen entstehen (vgl. Abb. 17).
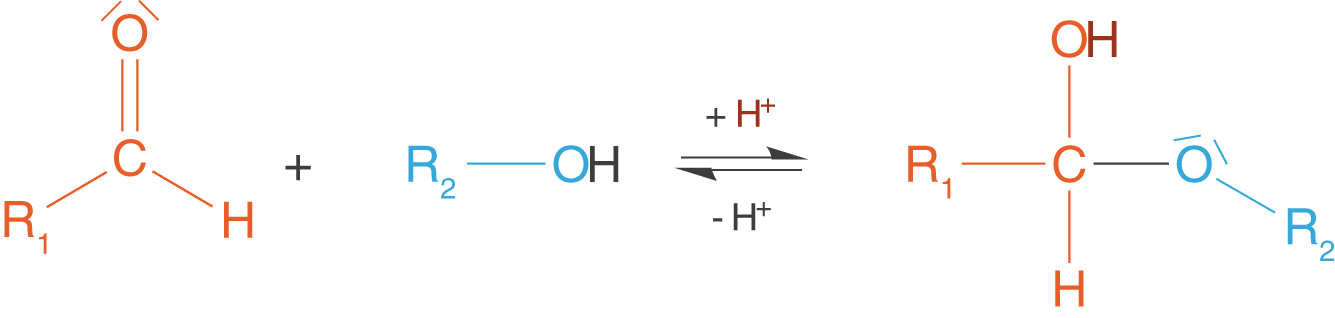
Wir wollen nun die -D-Glucose heranziehen und die Bildung des Halbacetals im Fall von Monosacchariden betrachten.
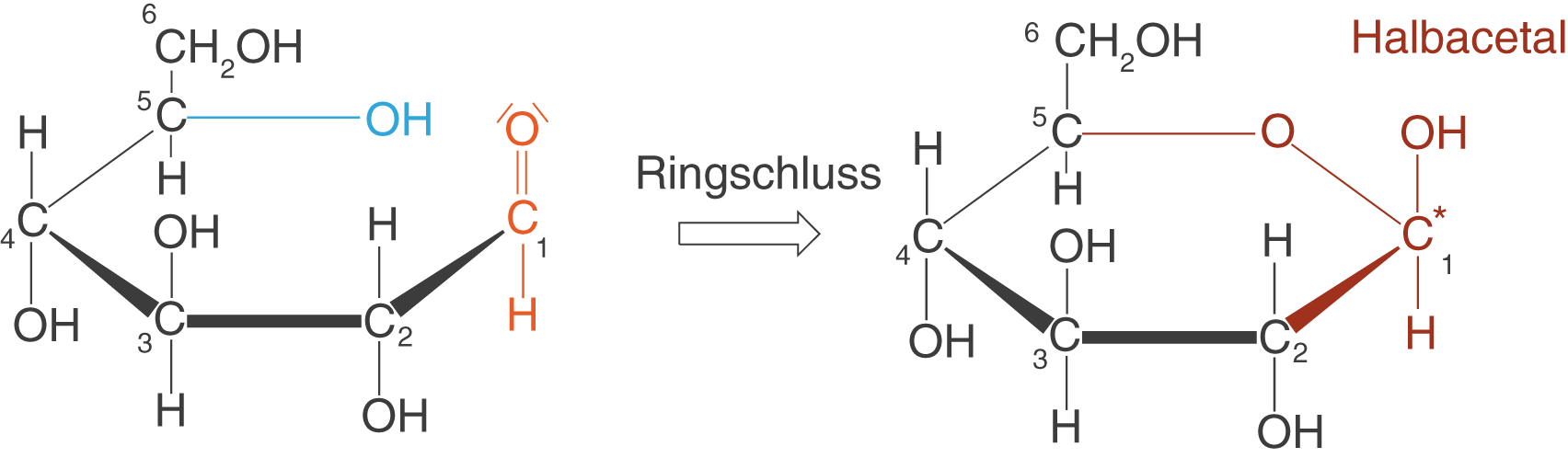
Wenn du dir die offenkettige Form der -D-Glucose anschaust (vgl. Abb. 18), dann erkennst du die für den Ringschluss relevante Hydroxygruppe (hier blau) und die relevante Aldehydgruppe (hier orange). Wir haben hier also beide funktionelle Gruppen vorliegen, die uns laut der Reaktionsgleichung in Abbildung 17 erlauben, ein Halbacetal auszubilden. Der interessante Aspekt besteht darin, dass beide funktionelle Gruppen Teil desselben Moleküls sind. Somit führt die Halbacetalbildung zum Ringschluss. Da diese Reaktion innerhalb des Moleküls abläuft, spricht man hier auch von der Bildung eines intramolekularen Halbacetals.
Zucker in wässrigen Lösungen
Glucose zeigt in wässrigen Lösungen zwei interessante Eigenschaften, die wir uns hier genauer anschauen wollen. Dabei handelt es sich um
- die Mutarotation, die im Zusammenhang mit der optischen Aktivität von Glucose steht.
- das Phänomen der Keto-Enol-Tautomerie, die es notwendig macht, einen spezifischen Test für Glucose zu haben.
Mutarotation am Beispiel der Glucose
Aus 3.1.2 wissen wir, dass Glucose optisch aktiv ist und die beiden Enantiomere -D-Glucose sowie
-L-Glucose ausbildet. Lösen wir
-D-Glucose in Wasser, dann können wir mithilfe des Polarimeters eine spezifische Drehung von
(bei
und Na-D-Lampe) messen. Erstaunlicherweise nimmt diese spezifische Drehung über einen gewissen Zeitraum auf
ab. Die Erklärung für dieses Phänomen liegt in der Eigenschaft der Mutarotation der Glucose begründet. In wässriger Lösung stellt sich schnell ein Gleichgewicht zwischen
-D-Glucose, der offenkettigen Form und dem Anomer
-D-Glucose ein (vgl. Abb. 19).
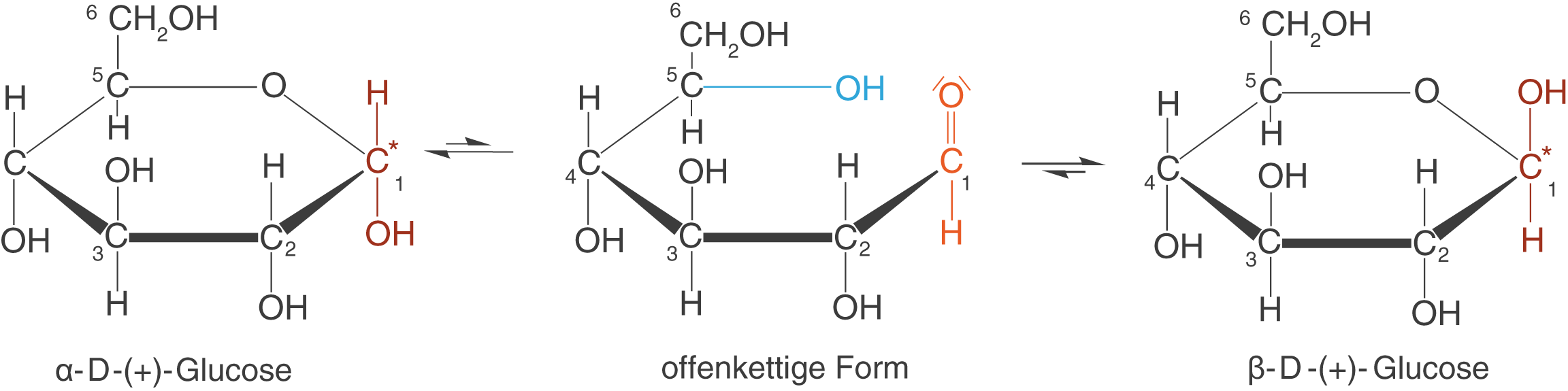
Hierbei liegt das Gleichgewicht jeweils auf den Seiten der Anomere, was bedeutet, dass die offenkettige Form nur in sehr geringen Anteil in der Lösung vorliegt. Dadurch, dass die spezifische Drehung der -D-(+)-Glucose mit
deutlich kleiner ist als die spezifische Drehung der
-D-(+)-Glucose, kommt es im Falle des Gleichgewichts auch zu einem anteilsmäßigen Mittelwert der beiden spezifischen Drehungen, der dem beobachteten entspricht. Vergleiche hierzu die Optische Aktivität von Gemischen im ChemieLV-Skript Stereoisomerie und optische Aktivität.
Keto-Enol-Tautomerie von D-Fructose und D-Glucose
Die Keto-Enol-Tautomerie
Lösen wir Fructose in Wasser, dann können wir nach einiger Zeit interessanterweise einen reduzierenden Zucker (vgl. Kapitel 4) nachweisen, obwohl Fructose keine Aldehydgruppe, sondern eine Ketogruppe aufweist. Dieses Phänomen können wir mithilfe der Keto-Enol-Tautomerie erklären. Unter Tautomerie versteht man die gleichzeitige Verschiebung eines H-Atoms (Protons) und einer Doppelbindung (vgl. Abb. 22). Die Abbildungen 20 und 21 dienen dem Verständnis des Mechanismus der Keto-Enol-Tautomerie. Merken solltest du dir vor allem Abbildung 22.
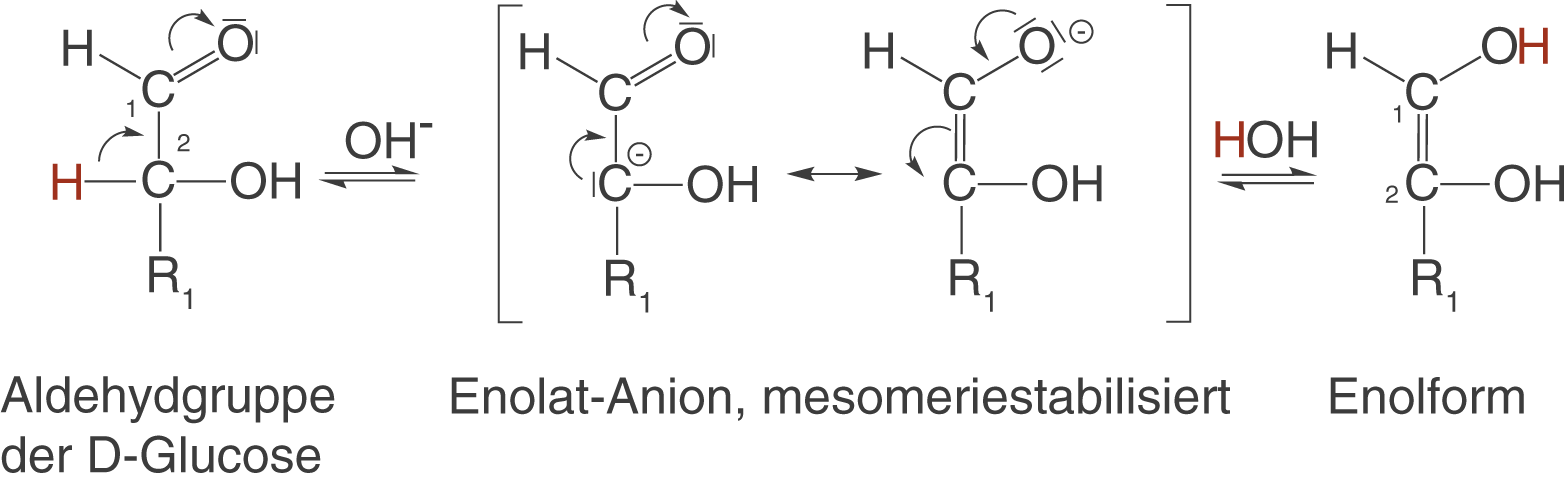
- Die Base
deprotoniert das C-2-Atom der D-Glucose.
- Es entsteht das mesomeriestabilisierte Enolat-Anion.
- Das in Schritt 1 erhaltene H-Atom bindet an ein freies Elektronenpaar des O-Atoms am C-1-Atom - die Enolform entsteht.
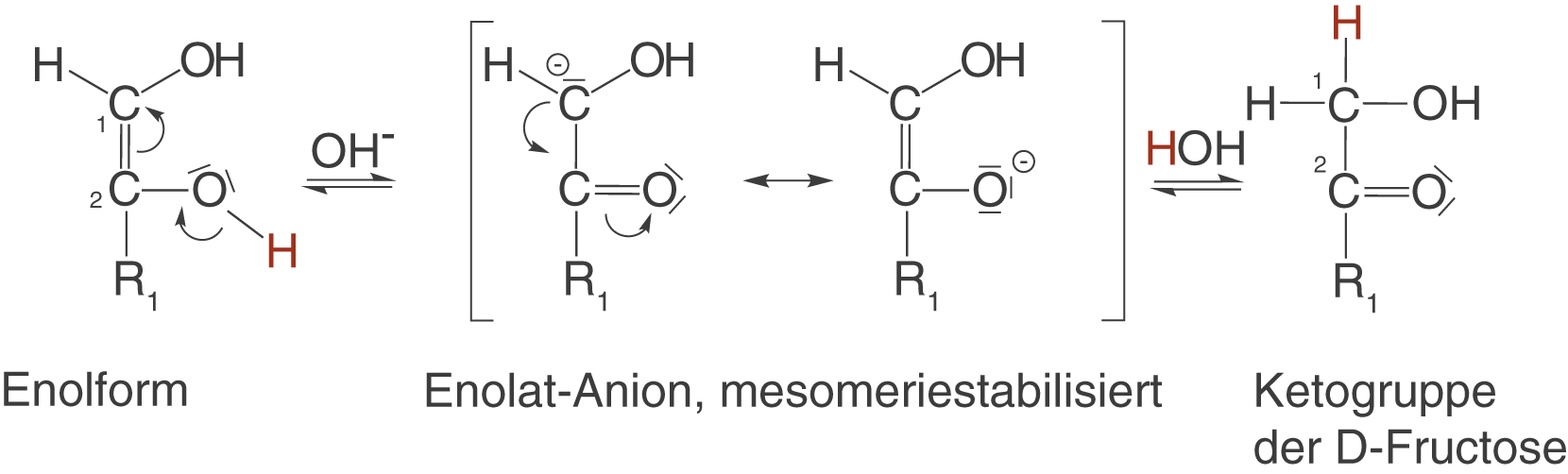
- Die Base
deprotoniert die Hydroxygruppe am C-2-Atom der Enolform.
- Es entsteht das mesomeriestabilisierte Enolat-Anion.
- Das in Schritt 1 erhaltene H-Atom bindet an ein freies Elektronenpaar des C-1-Atoms - die D-Fructose entsteht.
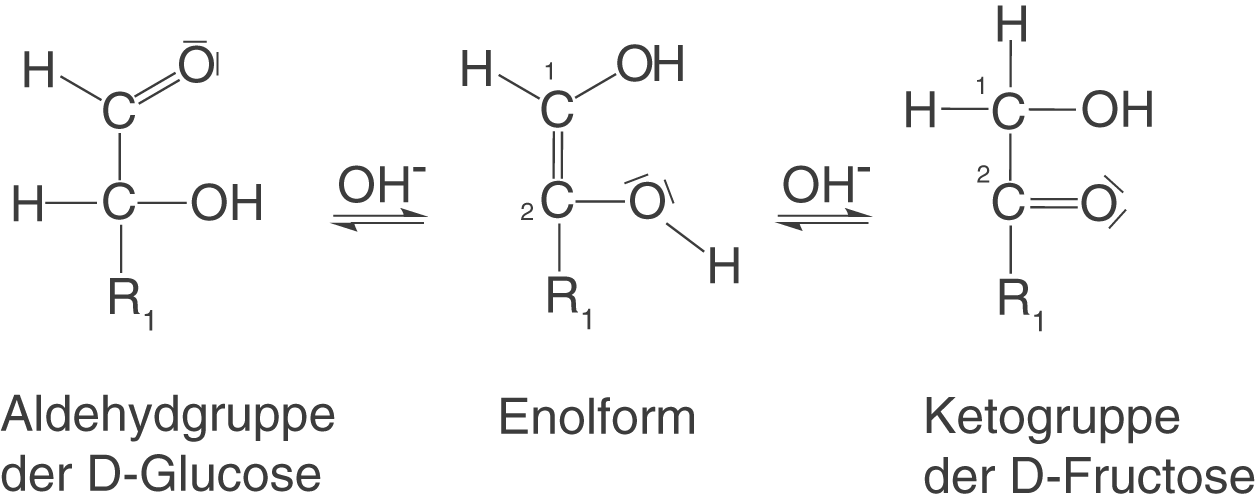
D-Glucose und D-Fructose stehen über die Enolform im Gleichgewicht (vgl. Abb. 22). Wichtig: Die Enolbildung findet auch im sauren Milieu statt.
Glucose-spezifischer Nachweis: der GOD-Test
In manchen Fällen ist es notwendig, Glucose spezifisch nachweisen zu können, etwa bei Diabetes-Patienten (Diabetes Mellitus). In Kapitel 4 sprechen wir die Möglichkeit des Nachweises reduzierender Zucker an. In diesem Fall ist die Aldehydgruppe der Glucose für den Nachweis relevant, da diese reduzierende Eigenschaften aufweist (s.u.). Hier kommt die Keto-Enol-Tautomerie ins Spiel: Die relevanten Nachweise der reduzierenden Zucker laufen im alkalischen Milieu () ab, was bedeutet, dass sich Fructose in Glucose umwandelt. Dementsprechend erhalten wir positive Testergebnisse, die nicht der ursprünglichen Zusammensetzung der Probe entsprechen.
Um dieses Problem zu umgehen, gibt es einen Glucose-spezifischen Nachweis: den Glucose-Oxidase-Test - kurz GOD-Test. Hierbei wird Glucose durch ein spezielles Enzym oxidiert, wobei die Reaktion unter geeigneten Bedingungen abläuft. Es kommt nicht zu verfälschenden Effekten.
Reduzierende Zucker und deren Nachweis
Saccharide, die eine freie Aldehydgruppe aufweisen, werden als reduzierende Zucker bezeichnet. Diese können sowohl Mono- und Oligo- als auch Polysaccharide sein, solange eine entsprechende Aldehydgruppe existiert. Die reduzierende Eigenschaft gründet sich darauf, dass die Aldehydgruppe bei Anwesenheit eines entsprechenden Oxidationsmittels zur Carboxygruppe oxidiert werden kann. Diese Eigenschaft erlaubt es, einige wichtige Nachweisreaktionen durchzuführen, die wir in diesem Skript beispielhaft für den Fall der Monosaccharide betrachten.
Die Fehling-Probe
Ein charakteristischer Nachweis für reduzierende Zucker ist die Fehling-Probe, welche im alkalischen Milieu () abläuft. Während dieser Reaktion wird die Eigenschaft der Aldehydgruppe genutzt, als Reduktionsmittel zu wirken, was bedeutet, dass sie Elektronen bereitstellt und oxidiert wird. Folgende Reagenzien kommen zum Einsatz:
- Fehling‘sche Lösung I: Kupfer(II)-sulfat-Lösung (hellblau)
- Fehling‘sche Lösung II: alkalische Kaliumnatriumtartrat-Lösung (farblos)
(a) Tartrat als Stabilisator
Die Redox-Reaktion findet im alkalischen Milieu mit -Kationen als Oxidationsmittel (Elektronenakzeptor) statt. Damit es nicht zu einem Ausfallen von Kupfer(II)-hydroxid (
) kommt, wird das Tartrat verwendet. Dieses bindet je ein
-Kation in Form einer Komplexverbindung und verhindert somit die Bildung des schwer löslichen Kupfer(II)-Salzes.
(b) Oxidation der Aldehydgruppe
Die Aldehydgruppe des Zuckers wird unter Elektronenabgabe zur Carbonsäure oxidiert:
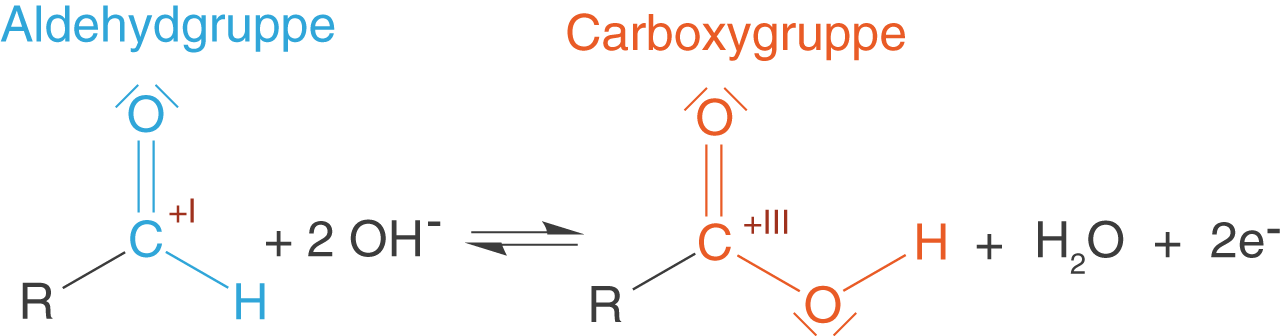
Und mit Summenformeln geschrieben:
(c) Reduktion von Cu2+
Kupfer(II)-Kationen werden im Alkalischen zu Kupfer(I)-Kationen reduziert und bilden einen ziegelroten Niederschlag ().
(d) Redox-Reaktion
Fassen wir die beiden Teilreaktionen zusammen, dann erhalten wir die Redox-Reaktion.
Zusammengefasst bedeutet das, dass Zucker mit einer freien Aldehydgruppe zur entsprechenden Carbonsäure oxidiert werden. Glucose wird beispielsweise zur Gluconsäure oxidiert.
Die Silberspiegel-/Tollensprobe
Ein weiterer klassischer Nachweis für reduzierende Zucker ist die Silberspiegel- oder Tollensprobe. Diese erhält ihren Namen dadurch, dass bei der Oxidation der Aldehydgruppe elementares Silber gebildet wird, welches den entsprechenden Silberspiegel bildet.
Folgende Reagenzien kommen zum Einsatz:
- Probesubstanz mit reduzierendem Zucker
- Ammoniakalische Silbernitrat-Lösung
(a) Reduktion von zu Ag
Das Silber liegt in Form eines Diamminsilber(I)-Komplexes vor und wird zu elementarem Silber reduziert.
(b) Oxidation der Aldehydgruppe
Die Oxidation der Aldehydgruppe läuft im alkalischen Milieu((c) Redox-Reaktion
Beim Zusammenfassen der Teilreaktionen müssen wir darauf achten, die Reaktionsgleichung der Reduktion mit dem Faktor zwei zu multiplizieren, um die richtige Menge an Elektronen zu erhalten. Damit ergibt sich:
Zusammenfassung
- Die Fischer-Projektion erlaubt die zweidimensionale Darstellung dreidimensionaler Molekülstrukturen.
- Veränderungen in der Anordnung der Substituenten in der Fischer-Projektion müssen mit Bedacht durchgeführt werden, da es sich um eine zweidimensionale Projektion handelt, in welcher dreidimensionale Informationen verloren gehen.
- Monosaccharide (Einfachzucker) sind die Monomere (die Bausteine) der Kohlenhydrate.
- Zwei der wichtigsten Monosaccharide sind die Fructose (Ketose) und die Glucose (Aldose).
- Mit einem Grundgerüst von 6 C-Atomen zählen die Glucose und Fructose zu den Hexosen mit der Summenformel
.
- Die Stellung der OH-Gruppen der Glucose merkst du dir mit dem Merkspruch: Ta-Tü-Ta-Ta, wobei die rechtsständigen OH-Gruppen mit Ta und die linksständige mit Tü bezeichnet wird.
- Die Stellung der OH-Gruppe des am weitesten von der Aldehyd- oder Ketogruppe entfernten asymmetrischen C-Atoms bestimmt die Benennung der Enantiomere: rechtsständig entspricht dem D-Enantiomer und linksständig dem L-Enantiomer.
- Die cyclische Form von Monosacchariden wird durch die Haworth-Projektion beschrieben.
- Der Ringschluss findet am neuen asymmetrischen C-Atom, dem anomeren C-Atom statt.
- Steht die OH-Gruppe am anomeren C-Atom in der Haworth-Projektion unten, dann handelt es sich um das
-Anomer; steht sie oben, dann handelt es sich um das
-Anomer.
- Cyclische Monosaccharide zählen zu den Halbacetalen.
- In wässrigen Lösungen stehen das
-Anomer und das
-Anomer der Glucose über die offenkettige Form im Gleichgewicht miteinander: Mutarotation.
- Im alkalischen Milieu stehen Glucose und Fructose durch die Keto-Enol-Tautomerie im chemischen Gleichgewicht. Ein Glucose-spezifischer Nachweis ist der Glucose-Oxidase-Test, kurz GOD-Test.
- Monosaccharide mit freien Aldehydgruppen zählen zu den reduzierenden Zuckern, da sie durch entsprechende Oxidationsmittel zu den entsprechenden Zuckersäuren oxidiert werden können.
- Bei der Fehling-Probe werden reduzierende Zucker durch die Reduktion von
nachgewiesen.
- Bei der Silberspiegel- oder Tollensprobe werden reduzierende Zucker durch die Reduktion von
nachgewiesen. Es entsteht elementares Silber, welches den charakteristischen Silberspiegel ausbildet.