SchulLV Logo

Reaktionsgleichungen und Stöchiometrie

Reaktionsgleichungen

Wenn wir uns in der Chemie über Reaktionen und die beteiligten Reaktanden unterhalten wollen, dann greifen wir zu den Reaktionsgleichungen. Diese erlauben uns chemische Reaktionen graphisch darzustellen und folgen einem einheitlichen Schema. Wir schauen uns in diesem Skript zunächst das Aufstellen von Reaktionsgleichungen an und lernen diese „auszugleichen“. Anschließend werfen wir einen Blick auf die wichtigsten Reaktionstypen, die dir in der Schule begegnen werden und besprechen diese vor dem gleichen Hintergrund. Der zweite Teil des Skripts widmet sich dann der Berechnung grundlegender Größen der Stöchiometrie, die wir mithilfe der Informationen aus den jeweiligen Reaktionsgleichungen gewinnen können.

Wichtig: Um den Sinn und Aufbau von Reaktionsgleichungen zu verstehen wird dir nichts anderes übrig bleiben selbst Hand anzulegen und die ein oder andere Reaktionsgleichung aufzustellen und auszugleichen. In diesem Skript helfen wir dir bei den Grundlagen, die du benötigst, um in das Thema einzusteigen. An dieser Stelle wollen wir dir schon einmal das ChemieLV-Lernvideo Reaktionsgleichungen und Stöchiometrie empfehlen, in welchem dir Juliane das Vorgehen ausführlich an ausgewählten Beispielen aufzeigt.

Grundlagen

Wie bei jeder Sprache müssen wir uns zu Beginn auf einige Regeln einigen, damit wirklich jeder die „gleiche Sprache spricht“ und die Verständigung überhaupt erst möglich wird.

Wichtig: Um eine reibungsfreie Verständigung zu gewährleisten, müssen wir uns auf eine gewisse Grundlage einigen und sicherstellen, dass sich jeder daran hält. Du redest ja auch nicht mit deinem Freund aus England in deinem lokalen Dialekt, sondern verständigst dich mit ihm in Englisch. Die gleiche Situation haben wir hier: verwendest du andere Symbole, dann wissen die anderen nicht von was du sprichst oder was du meinst. Versuche dir deshalb die vorgegebenen Symbole zu merken und verwende sie. Dann ist eine einwandfreie Verständigung möglich!

Ganz allgemein setzt sich eine Reaktionsgleichung aus drei Bestandteilen zusammen:

  1. Auf der linken Seite stehen die Edukte.
  2. Auf der rechten Seite stehen die Produkte.
  3. Zwischen Edukten und Produkten steht der Reaktionspfeil.

Die Edukte und die Produkte schreiben wir in Form von Summenformeln. Für die einzelnen Elemente verwenden wir die entsprechenden Elementsymbole aus dem Periodensystem der Elemente (vgl. Abb. 1). Ein Aspekt in Abbildung 1 ist besonders wichtig: Der Unterschied zwischen dem stöchiometrischen Koeffizienten und der Anzahl der Atome des \(\text{H}_{2}\)-Moleküls im Index. Die Zahl im Index (tiefgestellt) des Elementsymbols ist relevant für die Verbindung die reagiert. Das bedeutet, dass wir von zwei unterschiedlichen Sachen sprechen, wenn wir statt \(\text{H}_{2}\) nur H schreiben würden. Diese Zahl wird nie verändert, wenn wir eine Reaktionsgleichung ausgleichen!

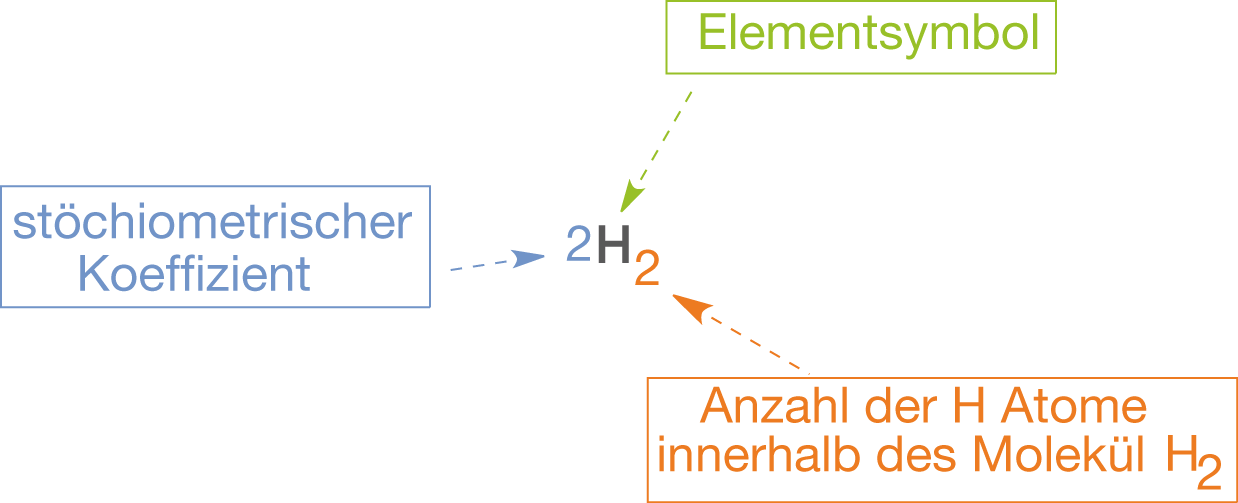Abb. 1: Darstellung eines Reaktanden in einer Reaktionsgleichung

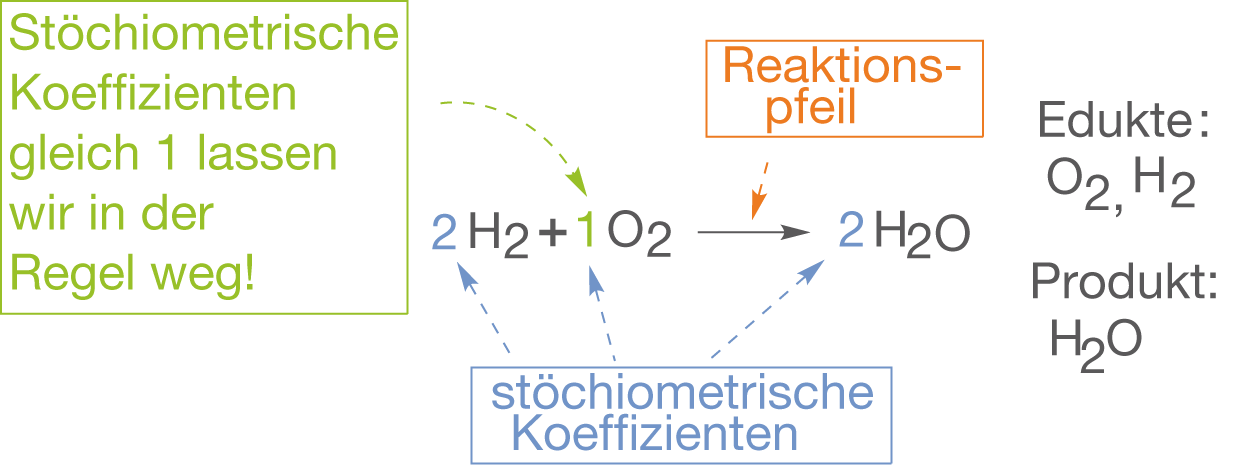
Reagieren mehrere Edukte des selben Typs, dann schreiben wir die entsprechende Anzahl in Form eines Faktors vor die Summenformel des jeweiligen Edukts. Das gleiche gilt für den Fall, dass mehrere Produkte vom gleichen Typ durch die Reaktion gebildet werden. Die angesprochenen Faktoren nennen wir stöchiometrische Koeffizienten. In Abbildung 2 siehst du beispielhaft eine Reaktionsgleichung mit allen bisher genannten Bestandteilen:


Abb. 2: Eine Reaktionsgleichung

Bezüglich der Reaktionspfeile hat man sich auf zwei Exemplare geeinigt:

  • \(\longrightarrow\): Nicht-Gleichgewichtsreaktionen
  • \(\rightleftharpoons\): Gleichgewichtsreaktionen

Es werden genau diese beiden Pfeile für Reaktionsgleichungen verwendet, um ein „reagiert zu“ zu symbolisieren. Alle anderen Pfeile sind falsch.

Reaktionsgleichungen I: Aufstellen und Ausgleichen

Wir wollen nun damit beginnen bei gegebenen Edukten und Produkten eine Reaktionsgleichung zu formulieren. Dazu nehmen wir die Nicht-Gleichgewichtsreaktion von elementarem Natrium mit elementarem Chlor, welche als Produkt Natriumchlorid hervorbringt.

1. Aufstellen der Reaktionsgleichung

Natrium hat das Elementsymbol Na und Chlor hat das Elementsymbol Cl. Nun wissen wir aber, dass alle Halogene elementar als zweiatomige Moleküle vorliegen. Also sprechen wir von \(\boldsymbol{\text{Cl}_{2}}\) und nicht von \(\text{Cl}\). Damit können wir die Reaktionsgleichung aufstellen:

\(\text{Na}+\text{Cl}_{2} \longrightarrow \text{NaCl}\)

In Worten: „Natrium reagiert mit Chlor zu Natriumchlorid“.

2. Ausgleichen der Reaktionsgleichung

Schauen wir uns die Reaktionsgleichung genauer an, dann fällt auf, dass auf der Seite der Edukte (links) zwei Chloratome in Form eines \(\text{Cl}_{2}\)-Moleküls vorliegen, wohingegen wir aktuell auf der Produktseite (rechts) nur ein \(\text{Cl}\) in \(\text{NaCl}\) vorliegen haben. Wir gleichen aus, indem wir die Produktseite mit einem stöchiometrischen Koeffizienten multiplizieren, sodass wir letztendlich zwei Chloratome vorfinden:

\(\text{Na}+\text{Cl}_{2} \longrightarrow 2\;\text{NaCl}\)

Nun haben wir auch auf der Produktseite formal zwei \(\text{Cl}\)-Atome vorliegen. Es fällt uns aber auf, dass sich durch das bisherige Vorgehen ein Fehler bei den \(\text{Na}\)-Atomen eingeschlichen hat: Auf der Eduktseite ist es immer noch ein \(\text{Na}\)-Atom, während auf der Produktseite durch den stöchiometrischen Faktor von 2 formal nun 2 \(\text{Na}\)-Atome vorliegen. Das bedeutet, dass wir nun auch noch das \(\text{Na}\) auf der Eduktseite ausgleichen, indem wir den entsprechenden stöchiometrischen Koeffizienten von 2 hier ebenfalls hinzufügen.

\(2\;\text{Na}+\text{Cl}_{2} \longrightarrow 2\;\text{NaCl}\)

Dieses Beispiel kannst du im ChemieLV-Lernvideo Reaktionsgleichungen live nachvollziehen.

Achtung: Wir erhalten in dieser Reaktion ein Mol \(\text{NaCl}\); wir erhalten kein \(\text{NaCl}\)-Molekül. Soetwas exisitert nicht, da es sich bei \(\text{NaCl}\) um ein Salz handelt und sich ein solches in Form eines Kristalls aufbaut. Dieser Kristall kann nicht nur aus zwei Ionen bestehen!

3. Zusatzinformationen hinzufügen

Unter Umständen kann es interessant sein weitere Informationen zur Reaktionsgleichung hinzuzufügen. Darunter können beispielsweise folgende fallen:

  • Aggregatszustände der Reaktanden: gasförmig (g), flüssig (l), fest (s)
  • Stoffe gelöst in Wasser (aq)
  • Reaktionsbedingungen werden auf oder unter den Reaktionspfeil geschrieben, bspw. \(\Delta E\) (Aktivierungsenergie) oder Katalysatoren.

Für unsere Reaktion können wir bspw. noch die Aggregatszustände der Reaktanden hinzufügen, indem wir die genannten Kürzel zum jeweiligen Elementsymbol zusätzlich in den Index schreiben.

\(2\;\text{Na}_{(\text{s})}+\text{Cl}_{2\,(\text{g})} \longrightarrow 2\;\text{NaCl}_{(\text{s})}\)

Hierbei ist es jedoch natürlich notwendig diese Aggregatszustände zu kennen.

Reaktionsgleichungen II: Säure-Base-Reaktionen

Ladungen in einer Reaktionsgleichung

Unter 1.2 haben wir eine relativ einfache Reaktionsgleichung ausgeglichen, bei welcher wir uns nur mit der Anzahl der beteiligten Atome beschäftigen mussten. Nun gehen wir zu den Säure-Base-Reaktionen über, die eine zentrale Rolle in der Chemie einnehmen. Hierbei handelt es sich nun um Gleichgewichtsreaktionen. Wir wollen hierfür ein prominentes Beispiel verwenden, dass auch an verschiedenen Stellen im ChemieLV-Basiswissen bereits zur Sprache kam: Die Säure-Base-Reaktion von Kohlensäure mit Wasser.

1. Aufstellen der Reaktionsgleichung

Kohlensäure (\(\text{H}_{2}\text{CO}_{3}\)) reagiert mit Wasser (\(\text{H}_{2}\text{O}\)) zu Hydrogencarbonat (\(\text{HCO}_{3}^{-}\)) und einem Oxonium-Ion (\(\text{H}_{3}\text{O}^{+}\)).

\(\text{H}_{2}\text{CO}_{3}+\text{H}_{2}\text{O} \rightleftharpoons \text{HCO}_{3}^{-}+\text{H}_{3}\text{O}^{+}\)

2. Ausgleichen der Reaktionsgleichung

Bevor wir dazu übergehen umständlich die Anzahl einzelner Elemente zu zählen, überlegen wir uns zunächst einmal, was bei einer Säure-Base-Reaktion überhaupt geschieht. In unserem Fall wurde ein \(\text{H}^{+}\) von der Kohlensäure zum Wasser übertragen. Mehr ist in der Tat nicht passiert. Das bedeutet, dass die Reaktion bereits ausgeglichen ist. Um das zu überprüfen, zählen wir auf der Eduktseite und Produktseite jeweils vier H-Atome. Da diese effektiv die einzigen beteiligten Reaktanden waren, stimmt unsere Reaktion.

\(\text{H}_{2}\text{CO}_{3}+\text{H}_{2}\text{O} \rightleftharpoons \text{HCO}_{3}^{-}+\text{H}_{3}\text{O}^{+}\)

Dennoch lohnt es sich hier einen genauere Blick auf die Seite der Edukte zu werfen: Dort liegen geladenen Ionen vor. Ladungen innerhalb einer Reaktionsgleichung müssen immer ausgeglichen sein, d.h. die Ladung der Eduktseite muss der Ladung auf der Produktseite entsprechen. Klären wir das am Beispiel unserer Protolysereaktion:

  • Die Edukte sind alle ungeladen, was hier eine Gesamtladung von 0 ergibt.
  • Ein Produkt ist einfach positiv geladen, während das andere einfach negativ geladen ist. In der Summe ist also auch die Produktseite neutral.
  • Damit entspricht die Ladung der Eduktseite der Ladung der Produktseite.

Zusammenfassen von Reaktionsgleichungen

Im Fall der Protolyse von Kohlensäure entsteht ein weiteres Molekül, das in Wasser als Säure wirkt: das Hydrogencarbonat-Anion (\(\text{HCO}_{3}^{-}\)).

1. Aufstellen der Reaktionsgleichung

Formulieren wir zunächst die Reaktionsgleichung für die Reaktion von Hydrogencarbonat mit Wasser.

\(\text{HCO}_{3}^{-}+\text{H}_{2}\text{O} \rightleftharpoons \text{CO}_{3}^{2-}+\text{H}_{3}\text{O}^{+}\)

2. Ausgleichen der Reaktionsgleichung

Wiederum haben wir nur ein Proton (\(\text{H}^{+}\)) übertragen, sodass die Reaktionsgleichung bereits ausgeglichen ist.

3. Zusammenfassen von Reaktionsgleichungen

Nun könnten wir uns überlegen, dass die Reaktion von Kohlensäure in Wasser im Allgemeinen vielleicht auch noch weiter abläuft und zwar so wir wir es gerade im zweiten Beispiel gesehen haben. Wollen wir nun die Reaktionsgleichung der kompletten Dissoziation von Kohlensäure in Wasser formulieren, dann können wir dieses Vorhaben auf Grundlage der beiden bekannten Reaktionsgleichungen umsetzen. Dazu schreiben wir beide Reaktionsgleichungen untereinander:


\(\begin{array}{rcl} \text{H}_{2}\text{CO}_{3}+\text{H}_{2}\text{O}&\rightleftharpoons&\text{HCO}_{3}^{-}+\text{H}_{3}\text{O}^{+} \\ \text{HCO}_{3}^{-}+\text{H}_{2}\text{O}&\rightleftharpoons&\text{CO}_{3}^{2-}+\text{H}_{3}\text{O}^{+} \end{array}\)

Nun können wir diese beiden Reaktionsgleichungen addieren, so wie wir es aus der Mathematik kennen. Dazu addieren wir die Edukte und die Produkte aufeinander und erhalten:

\(\text{H}_{2}\text{CO}_{3}+2\;\text{H}_{2}\text{O}+\text{HCO}_{3}^{-}\) \(\rightleftharpoons\) \(\text{CO}_{3}^{2-}+2\;\text{H}_{3}\text{O}^{+}+\hspace{.2cm}\text{HCO}_{3}^{-}\)

Auf der Seite der Produkte haben wir nun zwei Oxonium-Ionen vorliegen, was wir durch einen stöchiometrischen Koeffizienten von 2 verdeutlichen können. Das gleiche gilt für das Wasser auf der Eduktseite. Du kannst nun sehen, dass sowohl auf der Eduktseite als auch auf der Produktseite das Hydrogencarbonat-Anion auftritt. Wir können die Reaktionsgleichung noch weiter vereinfachen, indem wir dieses Molekül gleichsam auf beiden Seiten subtrahieren. Damit ergibt sich für die vollständige Dissoziation von Kohlensäure in Wasser folgende Reaktionsgleichung:

\(\text{H}_{2}\text{CO}_{3}+2\,\text{H}_{2}\text{O}\) \(\rightleftharpoons\) \(\text{CO}_{3}^{2-}+2\;\text{H}_{3}\text{O}^{+}\)

Zum Schluss überprüfen wir wieder die Ladungen auf beiden Seiten:

  • Auf der Eduktseite befinden sich keine elektrisch geladenen Moleküle, womit wir hier wieder eine neutrale Situation vorfinden.
  • Auf der Produktseite finden wir das zweifach negativ geladene Carbonat-Anion (\(\text{CO}_{3}^{2-}\)) sowie zwei einfach positiv geladene Oxonium-Ionen (\(\text{H}_{3}\text{O}^{+}\)). Damit gleichen sich die Ladungen hier ebenfalls aus, sodass wir insgesamt auch hier eine ladungsneutrale Situation vorliegen haben.

Reaktionsgleichungen III: Redox-Reaktionen

Neben den Säure-Base-Reaktionen, bei denen Protonen ausgetauscht werden, gibt es noch eine zweite sehr wichtige Klasse an Reaktionen: die Redox-Reaktionen. Im Falle von Redox-Reaktionen werden Elektronen ausgetauscht. Dieses Thema ist sehr umfangreich und die Redox-Reaktionen stellen die anspruchsvollsten Reaktionsgleichungen dar, die du im Rahmen der Schulchemie aufstellen und ausgleichen musst. Aus diesem Grund haben wir diesem Thema eine eigenes Skript im Themengebiet Elektrochemie mit dem Titel Redox-Reaktionen und Oxidationszahlen gewidmet. Dort findest du alle relevanten Grundlagen, eine allgemeine Darstellung der Redox-Reaktionsgleichungen sowie Redox-Reaktionen, die bei \(\text{pH}\neq7\) ablaufen und die zugehörigen Reaktionsgleichungen.

Grundlagen der Stöchiometrie

Wenn wir uns noch einmal beispielhaft die Reaktion von Natrium mit Chlor zu Natriumchlorid anschauen, dann können wir sehen, dass uns diese primär zwei Arten von Informationen liefert:

  1. Qualitative Informationen: Wir kennen die Reaktanden, wissen welche miteinander reagieren und kennen die Produkte. Ganz einfach ausgedrückt: Wir können sagen, was miteinander reagiert.
  2. Quantitative Informationen: Die stöchiometrischen Koeffizienten einer Reaktionsgleichung geben uns Auskunft über die Anzahl der miteinander reagierenden Verbindungen. Wir können sagen, wieviel der Reaktanden miteinander reagieren und wieviel Produkt gebildet wird.

Im Rahmen der Stöchiometrie interessieren wir uns für die quantitativen Informationen, die uns eine Reaktionsgleichung liefern kann, um damit dann interessante Größen zu berechnen. Die wichtigsten dieser Größen lernen wir im Laufe dieses Kapitels kennen. Die Stöchiometrie geht hierbei auf einige sehr alte (frühes 19. Jahrhundert) Gesetze zurück, die wir uns heute immer noch zu Nutze machen:

  1. Die Massenerhaltung: Die Gesamtmasse der Reaktanden einer chemischen Reaktion ist konstant. Das bedeutet, dass die Masse der Edukte der Masse der gebildeten Produkte entspricht. Es wird keine Masse vernichtet oder erzeugt!
  2. Das Gesetz der konstanten Proportionen: Die Masse der Elemente innerhalb einer bestimmten chemischen Verbindung stehen in einem konstanten Verhältnis zueinander.
  3. Das Gesetz der multiplen Proportionen: Die Massenanteile von Elementen in verschiedenen chemischen Verbindungen stehen in einem ganzzahligen Verhältnis zueinander.
Anmerkung: Die Massenerhaltung ist bei chemischen Reaktionen nur annähernd gewährleistet. Es gibt Effekte, die dafür sorgen, dass eine minimale Abnahme der Masse während einer Reaktion zu verzeichnen ist. Diesen sogenannten Massendefekt können wir jedoch ignorieren, da er sehr gering ausfällt.

Das Stoffmengenverhältnis

Willst du eine Größe mithilfe der Stöchiometrie berechnen, dann steht am Anfang immer die Frage nach dem Stoffmengenverhältnis der relevanten Reaktanden. Wenn du dir folgendes Schema merkst, dann hast du in jedem Fall eine gute Ausgangssituation um unbekannte Größen zu berechnen, ohne dass du unsicher werden müsstest oder den Überblick verlieren würdest.

  1. Stelle zuerst die Reaktionsgleichung auf und gleiche diese aus.
  2. Stelle anschließend immer zuerst das Stoffmengenverhältnis auf, bevor du dich daran machst irgendeine andere Größe zu berechnen!

Die Stoffmenge \(n\)

Bevor wir dazu übergehen das Stoffmengenverhältnis für eine gegeben Reaktionsgleichung aufzustellen, wollen wir zunächst den Begriff der Stoffmenge klären. Die Stoffmenge besitzt das Formelzeichen \(\boldsymbol{n}\) und die Einheit Mol mit dem Einheitenkürzel mol. Im Folgenden sind drei Fakten über die Stoffmenge und das Mol dargestellt, die wir anschließend besprechen wollen:

  1. Die Stoffmenge \(\boldsymbol{n}\) beschreibt eine Anzahl von Atomen oder Molekülen. Vereinfacht ausgedrückt beschreibt die Stoffmenge eine Anzahl von Objekten.
  2. Eine Stoffmenge von \(\boldsymbol{n=1\,\textbf{mol}}\) umfasst ca. \(\boldsymbol{6\cdot10^{23}}\) Teilchen.
  3. Die unter Punkt 2 genannte Zahl geht auf die Anzahl der Kohlenstoffatome zurück, die man in \(12\,\text{g}\) des reinen Kohlenstoffisotops \(^{12}\text{C}\) findet.

Vor allem die unter Punkt 2 genannte Zahl \(\boldsymbol{6\cdot10^{23}}\), die die Anzahl der Teilchen in einem Mol angibt solltest du dir merken. Sie ist so wichtig, dass sie eine eigene Bezeichnung besitzt: die Avogadro-Konstante \(\boldsymbol{N}_{\textbf{A}}\), die nach dem italienischen Chemiker Amedeo Avogadro benannt ist. Die Avogadro-Konstante ist als Teilchenanzahl \(N\) pro Stoffmenge \(n\) definiert und besitzt die Einheit \(\frac{1}{\text{mol}}\) bzw. anders geschrieben \(\text{mol}^{-1}\).

\(N_{\text{A}}=\dfrac{N}{n}=6\cdot10^{23}\,\dfrac{1}{mol}\)

Hier steht genau, dass was wir schon wissen: Ein Mol eines Stoffes umfasst \(\boldsymbol{6\cdot10^{23}}\) Teilchen.

Das Stoffmengenverhältnis

\(\blacktriangleright\) Aufstellen des Stoffmengenverhältnis

Wir betrachten wieder beispielhaft die Bildung von Natriumchlorid (\(\text{NaCl}\)) aus den Elementen.

\(2\,\text{Na}+\text{Cl}_{2} \longrightarrow 2\,\text{NaCl}\)

Zunächst ist es sehr wichtig zu wissen, dass dir die stöchiometrischen Koeffizienten Informationen über die Stoffmengen der Reaktanden in der Reaktion liefern. Das bedeutet in diesem Fall folgendes:

  • \(2\,\text{mol}\) Natrium (\(\text{Na}\)) und
  • \(1\,\text{mol}\) Chlor (\(\text{Cl}_{2}\))
  • reagieren zu \(2\,\text{mol}\) Natriumchlorid (\(\text{NaCl}\)).
Anmerkung: Dies ist der Idealfall, der uns an dieser Stelle ausreicht. Wichtig ist jedoch zu wissen, dass chemische Reaktionen oft „unstöchiometrisch“ ablaufen, was bedeutet, dass mindestens ein Reaktand im Überschuss vorliegt. Somit kann dieser nicht komplett umgesetzt werden.

Wir wollen uns nun daran machen, dass Stoffmengenverhältnis für die obige Reaktion aufzustellen. Dazu gehen wir folgendermaßen vor:

  1. Das relevante Edukt bestimmen.
  2. Das relevante Produkt bestimmen.
  3. Das Stoffmengenverhältnis der beiden Aufstellen.

Beispiel 1: Stoffmengenverhältnis \(\text{Na}\)/ \(\text{NaCl}\)

Uns interessiert hier beispielhaft wie das Stoffmengenverhältnis von Natrium und Natriumchlorid aussieht. Wir formulieren nun zunächst das besagte Stoffmengenverhältnis und klären anschließend das allgemeine Vorgehen:

\(\dfrac{n(\text{Na})}{n(\text{NaCl})}=\dfrac{2}{2}\)

Auf der linken Seite sehen wir das Verhältnis der Stoffmengen von \(\text{Na}\) und \(\text{NaCl}\) und auf der rechten Seite das Verhältnis der zugehörigen stöchiometrischen Koeffizienten. Auf der rechten Seite können wir noch kürzen und erhalten dann:

\(\dfrac{n(\text{Na})}{n(\text{NaCl})}=\dfrac{1}{1}=1\)

Hieraus erhalten wir folgende Information: Pro Mol Natriumchlorid benötigen wir ein Mol elementares Natrium.

Beispiel 2: \(\text{Cl}_{2}\)/ \(\text{NaCl}\)

Das in Beispiel 1 aufgestellte Stoffmengenverhältnis war in unserem Fall willkürlich gewählt. Aus diesem Grund wollen wir uns nun an das Stoffmengenverhältnis von Chlor und Natriumchlorid wagen.

\(\dfrac{n(\text{Cl}_{2})}{n(\text{NaCl})}=\dfrac{1}{2}\)

Aus der Reaktionsgleichung wissen wir, dass elementares Chlor mit einem stöchiometrischen Koeffizienten von 1 eingeht. Gleichzeitig ist aber auch jedes Chlormolekül aus zwei Chloratome aufgebaut, sodass aus einem Mol elementarem Chlor (\(\text{Cl}_{2}\)) zwei Mol \(\text{NaCl}\) gebildet werden können. Unter 2.2 werden wir dann sehen, wie wir aufbauend auf der hier erarbeiteten Ausgangssituation relevante Grundgrößen der Stöchiometrie berechnen können.

\(\blacktriangleright\) Beachtung von limitierende Reaktanden

Wie du sehen konntest interessierte uns im Fall des Stoffmengenverhältnis nur die Stoffmenge eines Edukts sowie die Stoffmenge eines Produkts. An dieser Stelle wollen wir uns an die Anmerkung zu Beginn von 2.1.2 erinnern. Viele Reaktionen laufen unstöchiometrisch ab. Das bedeutet, dass eines der Edukte im Überschuss vorliegt. Wir habe also effektiv die Situation, dass von einem Edukte viel zu viel vorhanden ist, als dass alles umgesetzt werden könnte. Diese Situation könnte beispielsweise so aussehen:

  1. Wir haben \(3\,\text{mol}\) elementares Natrium (\(\text{Na}\)) vorliegen.
  2. Wir haben \(1\,\text{mol}\) elementares Chlor (\(\text{Cl}_{2}\)) vorliegen.

Ziehen wir nun das Stoffmengenverhältnis von Natrium und Natriumchlorid aus Beispiel 1 heran, dann fällt uns auf, dass pro Mol Natriumchlorid ein Mol Natrium umgesetzt werden muss. Wir haben hier aber \(3\,\text{mol}\) Natrium vorliegen. Damit könnten wir bis zu \(3\,\text{mol}\) Natriumchlorid synthetisieren. Nun kommt jedoch der Knackpunkt an der ganzen Sache: Wir betrachten hier nur eines der beiden Edukte und haben das andere bisher vernachlässigt! Werfen wir nun einen Blick auf das elementare Chlor unter Berücksichtigung von Beispiel 2. Dort sehen wir, dass pro Mol elementaren Chlors 2 Mol Natriumchlorid gebildet wird. In unserem Fall haben wir genau \(1\,\text{mol}\) elementares Chlor vorliegen, womit wir letztendlich also genau \(2\,\text{mol}\) Natriumchlorid erhalten können. Das erscheint komisch: Gerade hatten wir doch noch gesehen, dass wir unter Berücksichtigung von Natrium \(3\,\text{mol}\) Natriumchlorid synthetisieren könnten. Hier schlägt nun der Einfluss des limitierenden Reaktanden in Form des elementaren Chlors zu. Ganz einfach ausgedrückt ist einfach nicht genug Chlor vorhanden, um wirklich \(3\,\text{mol}\) Natriumchlorid zu bilden. Da hier beide Edukte relevant sind, kann nur soviel Produkt gebildet werden, wie es im Rahmen des Reaktanden mit der geringsten Stoffmenge möglich ist! Damit können wir im Fall dieses Beispiels maximal \(2\,\text{mol}\) Natriumchlorid synthetisieren, da die Stoffmenge des elementaren Chlors die Ausbeute limitiert.

Anmerkung: Wenn du stöchiometrische Größen berechnen sollst, dann überprüfe immer zunächst, ob eines der Edukte limitierend ist.

Grundgrößen der Stöchiometrie

Wir wollen nun nach und nach einige der stöchiometrischen Grundgrößen kennen lernen und ihre Verbindung zur Stoffmenge \(n\) aufzeigen. Hier werden wir dann auch sehen, dass uns das Stoffmengenverhältnis hilft die Größen richtig zu berechnen.

Die Masse \(m\) und die Molare Masse \(M\)

Die Masse \(\boldsymbol{m}\) von verschiedenen Stoffen bezeichnen wir mit dem Formelzeichen \(m\) wobei die Einheit der Masse in SI-Einheiten das Gramm \([m]=\text{g}\) ist. Die Masse ist eine zentrale Größe, da wir uns oft dafür interessieren wieviel Gramm eines Stoffes durch eine Reaktion erhalten werden kann. Um die Masse \(m\) jedoch rechnerisch zu bestimmen, benötigen wir noch eine andere Größe: die Molare Masse \(\boldsymbol{M}\). Diese können wir auf Grundlage der Masse \(m\) und der Stoffmenge \(n\) definieren:

\(M=\dfrac{m}{n}\text{ mit }[M]=\dfrac{\text{g}}{\text{mol}}\)

Wir wussten bisher, dass in einem Mol eines Stoffes \(6\cdot10^{23}\) Teilchen enthalten sind. Gleichzeitig erscheint es aber logisch, dass diese Teilchen ganz unterschiedliche Massen aufweisen können. Es macht eben einen Unterschied, ob wir von Wasserstoffmolekülen oder Glucosemolekülen reden. Das Mol legt ja nur die Anzahl und nicht den Typ der Teilchen fest. Die Molare Masse \(\boldsymbol{M}\) liefert uns nun die Information bzgl. der Masse eines Mols eines bestimmten Stoffes. Die Molare Masse eines Elements entspricht seiner Massenzahl im PSE. Stellen wir die oben eingeführte Formel nach \(n\) um, dann erhalten wir:

\(n=\dfrac{m}{M}\)

Somit haben wir einen Ausdruck für die Stoffmenge \(n\). Stellen wir diesen für die im Stoffmengenverhältnis berücksichtigten Reaktanden auf, dann können wir das \(n\) ersetzen und unbekannte Größen berechnen. Im Folgenden siehst du ein Beispiel für das Stoffmengenverhältnis von \(\text{Na}\) und \(\text{NaCl}\).

\(\dfrac{n(\text{Na})}{n(\text{NaCl})}=\dfrac{\frac{m(\text{Na})}{M(\text{Na})}}{\frac{m(\text{NaCl})}{M(\text{NaCl})}}=1\)

Das Volumen \(V\) und das molare Volumen \(V_{\text{m}}\)

Neben der Masse \(m\) ist das Volumen \(\boldsymbol{V}\) eine weitere zentrale Größe. Wir können uns beispielhaft für das Volumen interessieren, das ein Gas oder eine Flüssigkeit bei einer bestimmten Temperatur einnimmt oder wir fragen nach dem Volumen eines Feststoffes, den dieser bei gegebener Masse einnimmt. Wir können an dieser Stelle nun auch einen Zusammenhang zwischen dem Volumen \(V\) und der Stoffmenge \(n\) in Form des molaren Volumens \(\boldsymbol{V_{\textbf{M}}}\) herstellen.

\(V_{\text{M}}=\dfrac{V}{n}\text{ mit }[V_{\text{M}}]=\dfrac{\ell}{\text{mol}}\)

Das molare Volumen gibt uns Auskunft über das Volumen, welches die \(6\cdot10^{23}\) Teilchen eines Mols einnehmen. Das können wir uns auch relativ gut vorstellen: Die kleinen Wasserstoffmoleküle werden wohl ein geringeres Volumen einnehmen, als die großen Glucosemoleküle.

Anmerkung: In der Schule wirst du das molare Volumen vorrangig im Zusammenhang mit Gasen antreffen. Deshalb haben wir hier auch die Einheit Liter pro Mol gewählt. In anderen Fällen ist es günstiger das molare Volumen in Kubikmeter (\(\text{m}^{3}\)) pro Mol anzugeben.

\(\blacktriangleright\) Molare Volumina von idealen Gasen

Das molare Volumen von idealen Gasen ist bei konstanter Temperatur konstant. Folgendes gilt es sich zu merken:

  1. Alle Gase, die du im Rahmen der Schul-Chemie behandelst werden als ideal betrachtet.
  2. Jedes Gas hat bei einer gegebenen Temperatur das gleiche molare Volumen.

Hierbei solltest du dir insbesondere zwei Zahlen merken:

  • Für \(T=273,15\,\text{K}\) ist \(V_{\text{M}}=22,4\,\dfrac{\ell}{\text{mol}}\).
  • Für \(T=298,15\,\text{K}\) ist \(V_{\text{M}}=24,5\,\dfrac{\ell}{\text{mol}}\).

Auf Grundlage dieser Werte kannst du bei gegebener Temperatur \(T\) und Volumen \(V\) eines bestimmten Gases sofort die Stoffmenge \(n\) berechnen, indem du die Formel oben nach \(n\) auflöst:

\(n=\dfrac{V}{V_{\text{M}}}\)
Anmerkung: Es scheint ein wenig seltsam, aber im Fall des idealen Gases hängt das molare Volumen nicht von der Größe der Gasmoleküle ab, sondern nur von der Temperatur \(T\).

Die Dichte \(\rho\) (Massendichte)

Wir wollen nun auf die Frage zu Beginn von 2.2.2 zurückkommen: Welches Volumen \(V\) nimmt ein Festkörper bei gegebener Masse \(m\) ein? Wir benötigen demnach eine Größe, die die Masse \(m\) und das Volumen \(V\) verknüpft. Hier kommt die Dichte \(\boldsymbol{\rho}\) ins Spiel.

\(\rho=\dfrac{m}{V}\text{ mit }[\rho]=\dfrac{\text{g}}{\text{m}^{3}}\)

Unter 2.2.1 haben wir gesehen, wie wir über die Stoffmenge \(n\) zur Masse \(m\) gelangen. Formen wir die Formel für die Dichte \(\rho\) nach \(m\) um, dann erhalten wir einen neuen Ausdruck, den wir unter Umständen statt der Masse einsetzen können.

\(m=\rho\cdot V\)

Die Stoffmengenkonzentration \(c\)

Die letzte Größe, die wir uns hier anschauen wollen ist die Stoffmengenkonzentration \(\boldsymbol{c}\). Diese Größe verknüpft die Stoffmenge \(n\) und das Volumen \(V\):

\(c=\dfrac{n}{V}\text{ mit }[c]=\dfrac{\text{mol}}{\ell}\)

Bei der Stoffmengenkonzentration haben wir es folglich mit dem Verhältnis einer Teilchenanzahl zu einem bestimmten Volumen zu tuen. Wenn wir uns auf ein festes Volumen von bspw. \(V=1\,\ell\) einigen, dann können wir die Stoffmenge \(n\) in diesem Volumen variieren und somit die Stoffmengenkonzentration ändern. Auch hier erhältst du durch Umstellen der Formel nach \(n\) einen Ausdruck, den du in das Stoffmengenverhältnis einsetzen kannst.

\(n=c\cdot V\)
Anmerkung: Hier sind viele verschiedene Formeln aufgetaucht, bei denen es schwer sein kann sich alle auf Anhieb zu merken. Deshalb beachte folgenden Tipp: Wenn du die Einheiten der einzelnen Größen kennst, dann kannst du dir alle Formeln ohne Problem herleiten. Merke dir also vorrangig die Größen und die zugehörigen Einheiten!
Bildnachweise [nach oben]
[1]
© SchulLV
[2]
© SchulLV