Vektorprodukt
Definition
Das Vektorprodukt
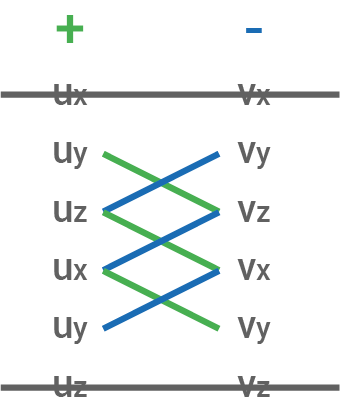
Merkhilfe zur Berechnung des Vektorprodukts:

Rechengesetze für das Vektorprodukt
Für alle Vektoren- Sind
und
Vielfache voneinander, so gilt
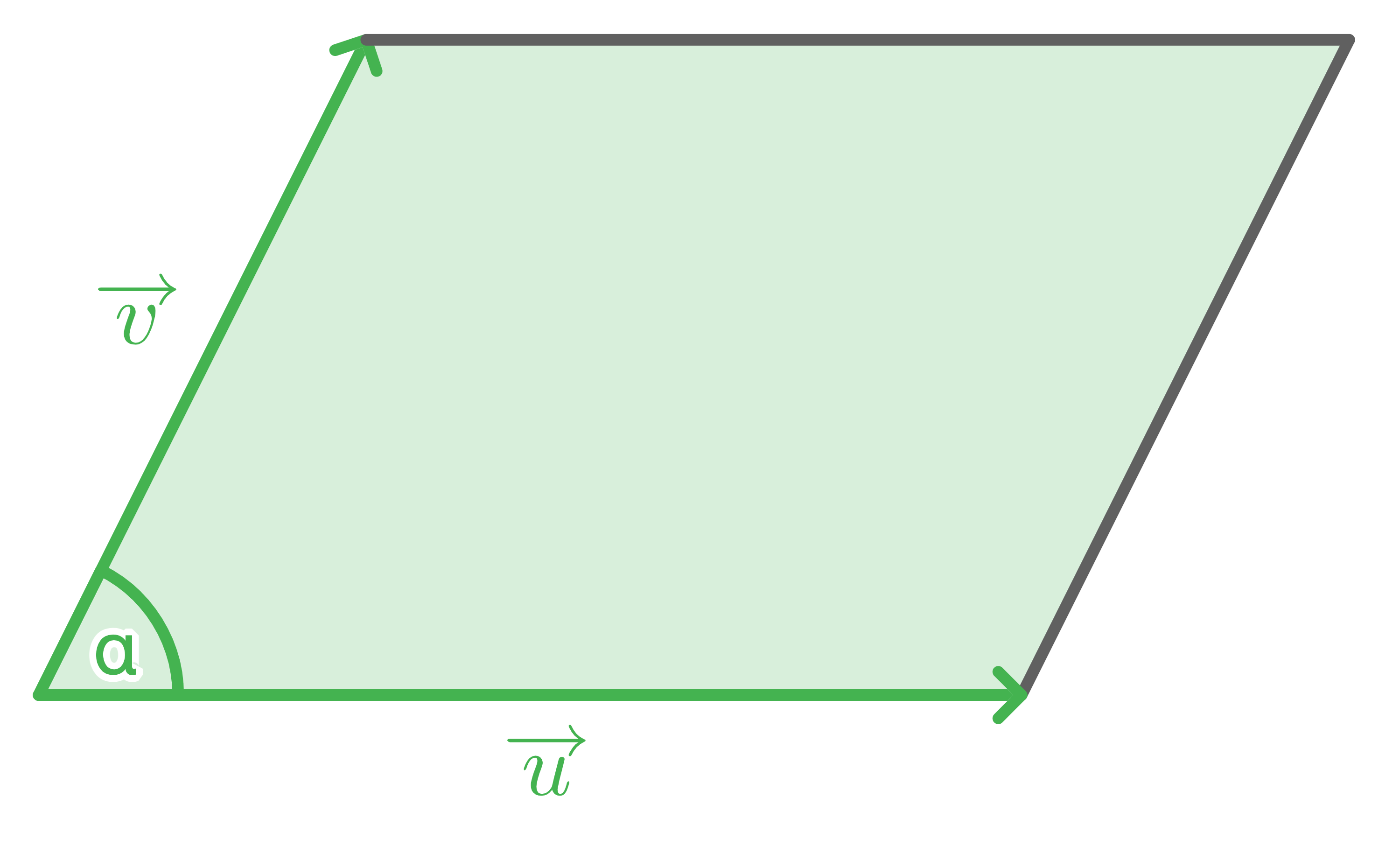
Flächeninhalt eines Parallelogramms
Das durch die beiden Vektoren  und
und  aufgespannte Parallelogramm hat den Flächeninhalt
aufgespannte Parallelogramm hat den Flächeninhalt 
1
Berechne das Vektorprodukt der Vektoren  und
und 



a)
b)
c)
2
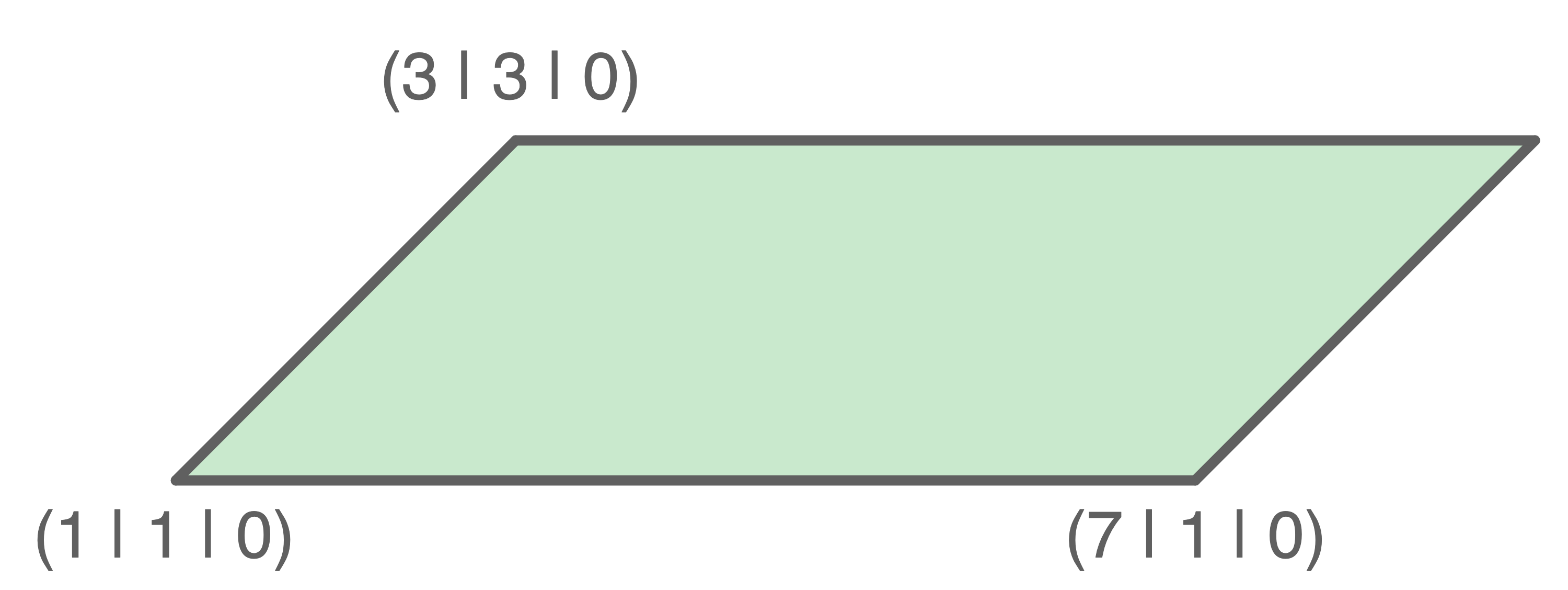
Bestimme den Flächeninhalt des Parallelogramms mit dem Vektorprodukt.

Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
b)
c)
2
Vektoren bestimmen

 Vektorprodukt berechnen
Vektorprodukt berechnen
![\(\begin{array}[t]{rll}
&\overrightarrow{u}\times \overrightarrow{v} \\[5pt]
&= \pmatrix{6\\0\\0}\times\pmatrix{2\\2\\0} \\[5pt]
&= \pmatrix{0\cdot 0-0\cdot 2\\0\cdot 2-6\cdot 0\\6\cdot 2-0\cdot 2} \\[5pt]
&= \pmatrix{0\\0\\12}
\end{array}\)](https://mathjax.schullv.de/7041328d02731244fb5962ba0965008dc4a7d1a1af88fa929028eb38ccc7df33?color=5a5a5a) Betrag berechnen
Betrag berechnen
 Das Parallelogramm hat einen Flächeninhalt von
Das Parallelogramm hat einen Flächeninhalt von 