Rechnen mit Vektoren

Addition von Vektoren

Der Vektor $\overrightarrow{s}=\overrightarrow{u}+\overrightarrow{v}$ $=\pmatrix{u_x\\u_y\\u_z}+\pmatrix{v_x\\v_y\\v_z}$ $=\pmatrix{u_x+v_x\\u_y+v_y\\u_z+v_z}$ heißt Summe oder auch Summenvektor von $\overrightarrow{u}=\pmatrix{u_x\\u_y\\u_z}$ und $\overrightarrow{v}=\pmatrix{v_x\\v_y\\v_z}.$

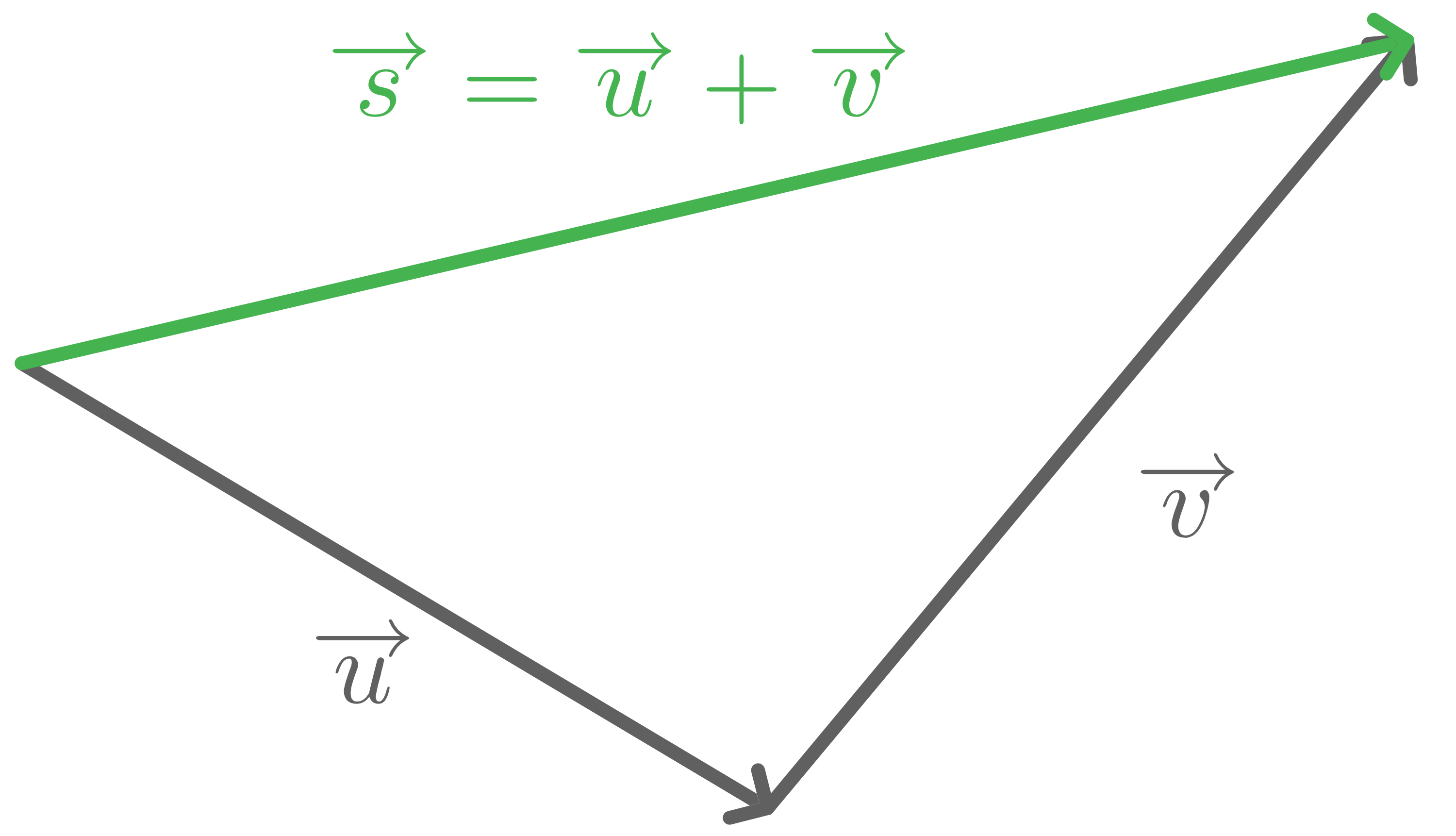
Anschaulich ergibt sich der Summenvektor $\overrightarrow{s}=\overrightarrow{u}+\overrightarrow{v},$ indem ein Pfeil für $\overrightarrow{v}$ an die Spitze eines Pfeils für $\overrightarrow{u}$ angehängt wird. Der Pfeil für $\overrightarrow{s}$ reicht dann vom Startpunkt des Pfeils von $\overrightarrow{u}$ bis zum Endpunkt des Pfeils von $\overrightarrow{v}.$

addieren von vektoren, summe zweier vektoren

Subtraktion von Vektoren

Der Vektor $\overrightarrow{d}=\overrightarrow{u}-\overrightarrow{v}$ $=\pmatrix{u_x\\u_y\\u_z}-\pmatrix{v_x\\v_y\\v_z}$ $=\pmatrix{u_x-v_x\\u_y-v_y\\u_z-v_z}$ heißt Differenz oder auch Differenzvektor von $\overrightarrow{u}=\pmatrix{u_x\\u_y\\u_z}$ und $\overrightarrow{v}=\pmatrix{v_x\\v_y\\v_z}.$

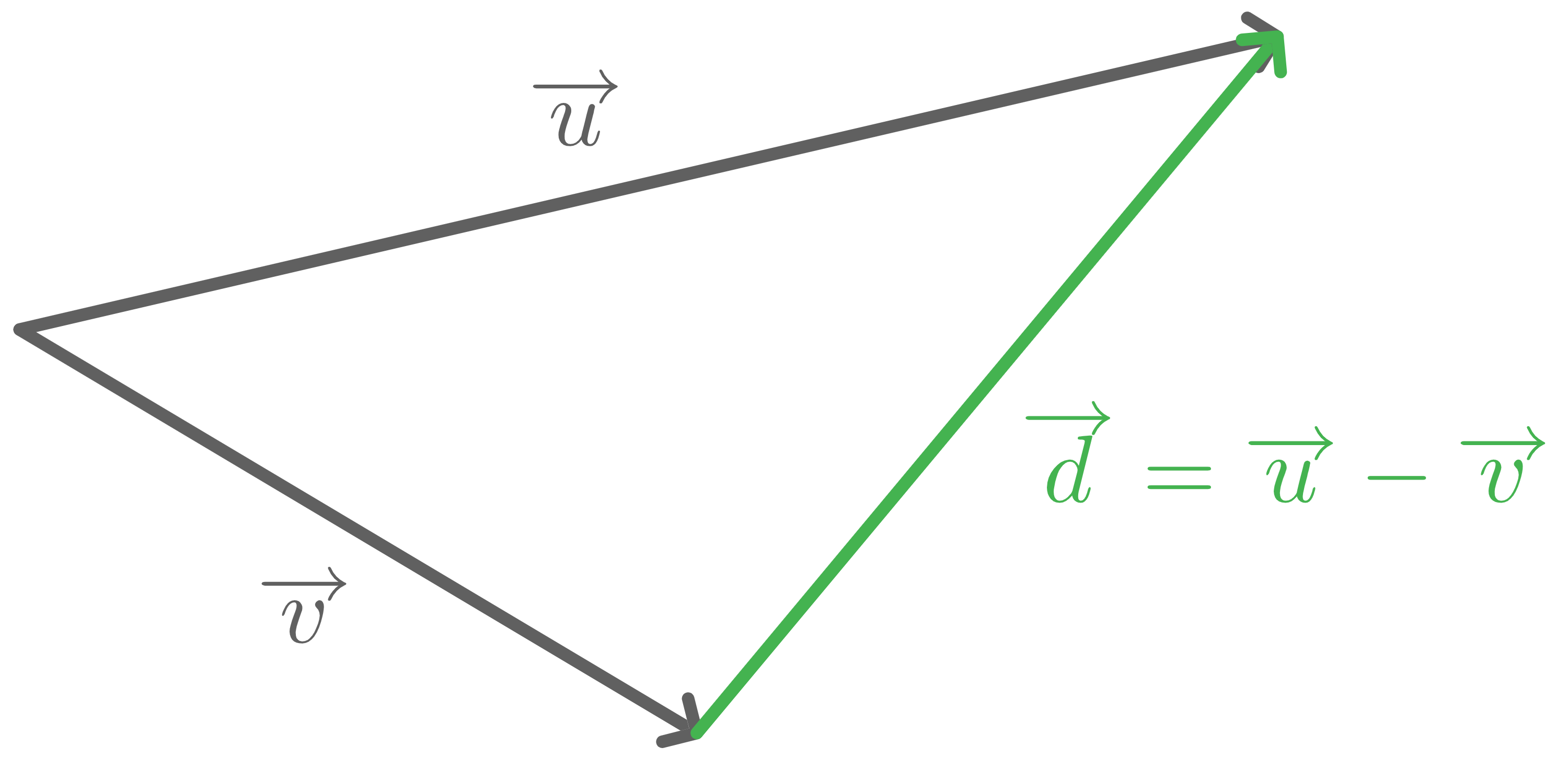
Anschaulich ergibt sich der Differenzvektor $\overrightarrow{d}=\overrightarrow{u}-\overrightarrow{v},$ indem Pfeile für $\overrightarrow{u}$ und $\overrightarrow{v}$ im gleichen Punkt abgetragen werden. Der Pfeil für $\overrightarrow{d}$ reicht dann vom Endpunkt des Pfeils von $\overrightarrow{u}$ bis zum Endpunkt des Pfeils von $\overrightarrow{v}.$

vektoren subtrahieren, differenz zweier vektoren

Der Pfeil des Differenzvektors $\overrightarrow{d}=\overrightarrow{u}-\overrightarrow{v}$ ergibt sich alternativ auch, indem an einen Pfeil für $\overrightarrow{u}$ ein Pfeil des Gegenvektors $-\overrightarrow{v}$ angehängt wird.

Abstand zweier Punkte

Der Abstand zweier Punkte $A(a_x\mid a_y\mid a_z)$ und $B(b_x\mid b_y\mid b_z)$ ist der Betrag des Vektors $\overrightarrow{AB}.$ Es gilt:

$\overline{AB}=|\overrightarrow{AB}|$ $=\sqrt{(b_x-a_x)^2+(b_y-a_y)^2+(b_z-a_z)^2}$