Stetige und diskrete Zufallsgrößen
Bisher wurden diskrete Zufallsgrößen behandelt, die nur endlich viele oder abzählbar unendlich viele Werte annehmen können. Zufallsgrößen, die dagegen in einem Intervall beliebig viele Werte annehmen können, heißen stetige Zufallsgrößen.
unterteilt.
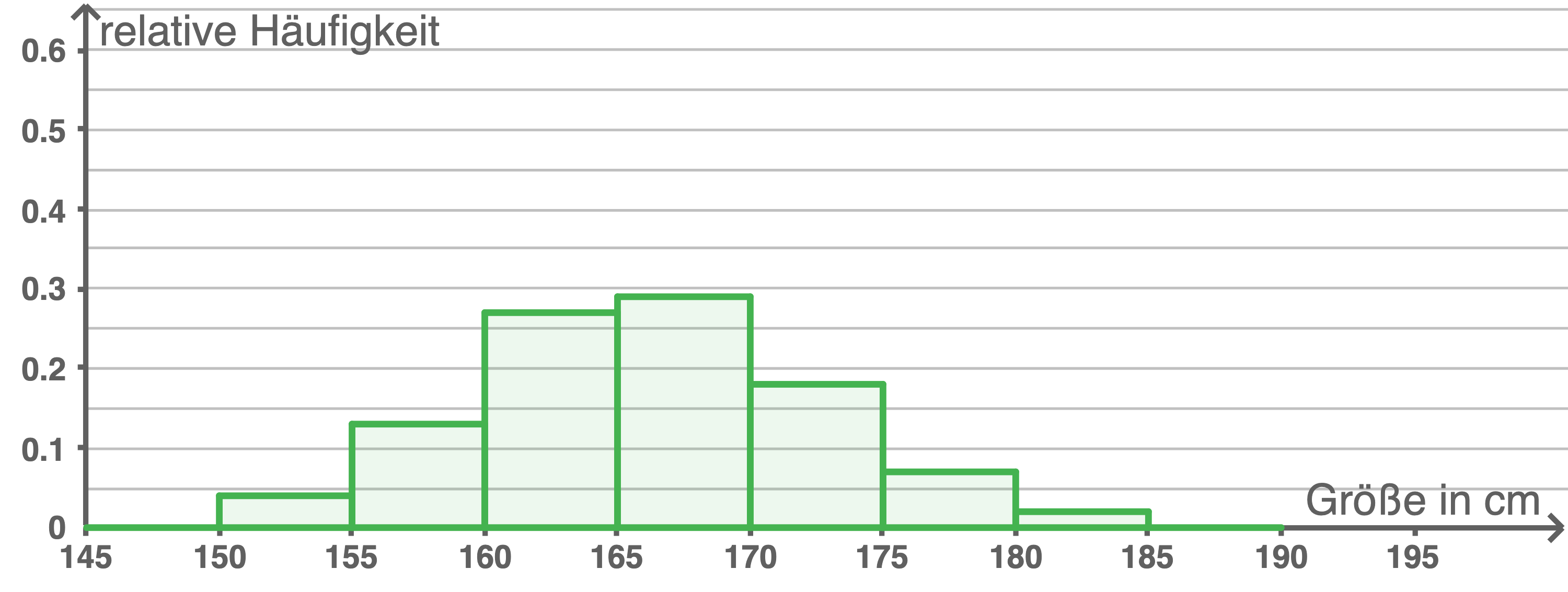Das Histogramm kann immer weiter verfeinert werden, indem die Intervalle verkleinert werden, beispielsweise auf eine Intervallgröße von 
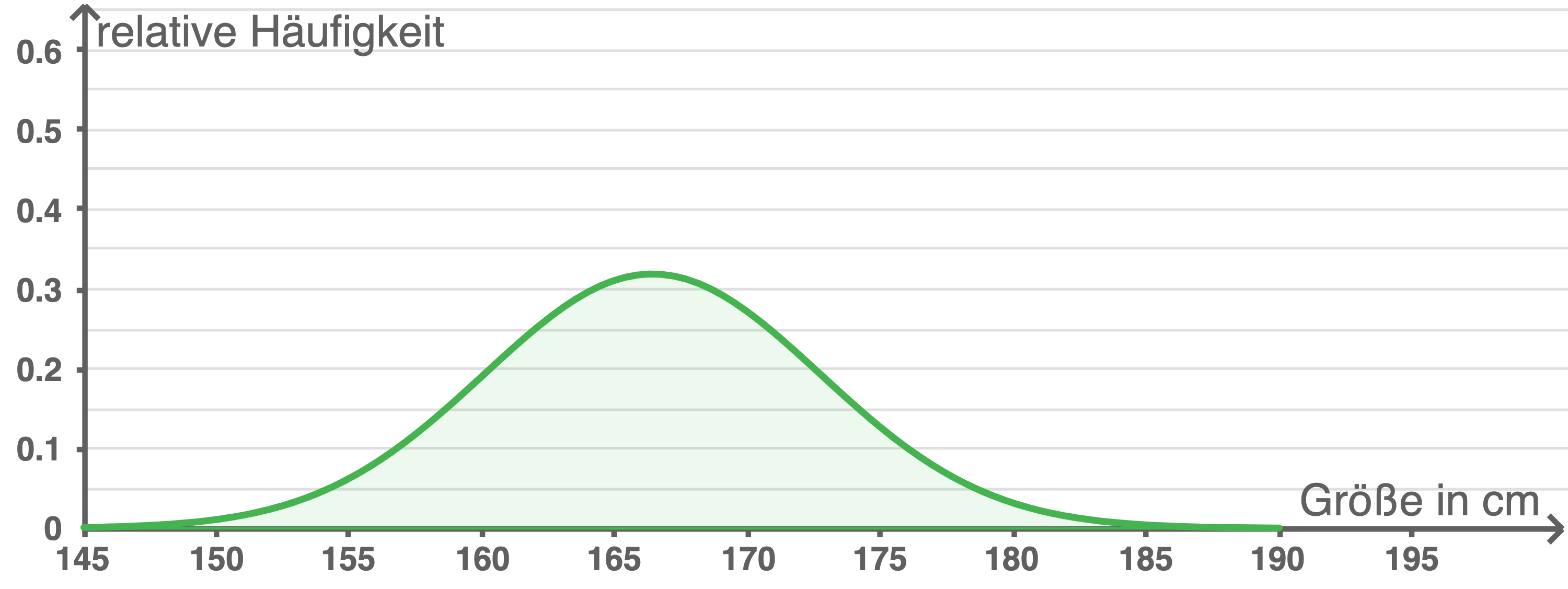
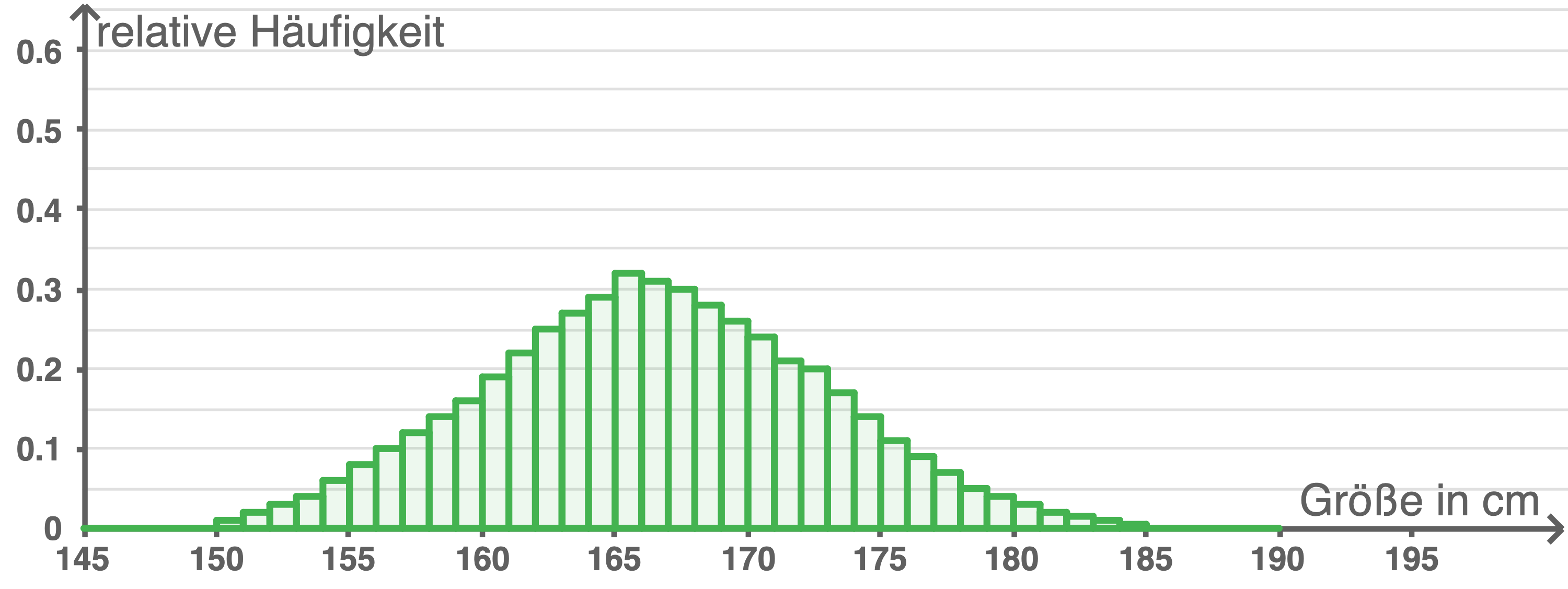Da theoreitsch jeder beliebige Wert angenommen werden kann, kann das Histogramm beliebig verfeinert werden, bis sich eine idealisierte Darstellung des Sachverhalts ergibt. Diese ist durch den Graphen einer stetigen Funktion gegeben, der sogenannten Dichtefunktion.
Beispiel
Die Körpergröße erwachsener Frauen in Deutschland ist im folgenden Histogramm dargestellt. Die Körpergröße ist dabei in Intervalle von
Normalverteilte Zufallsgrößen
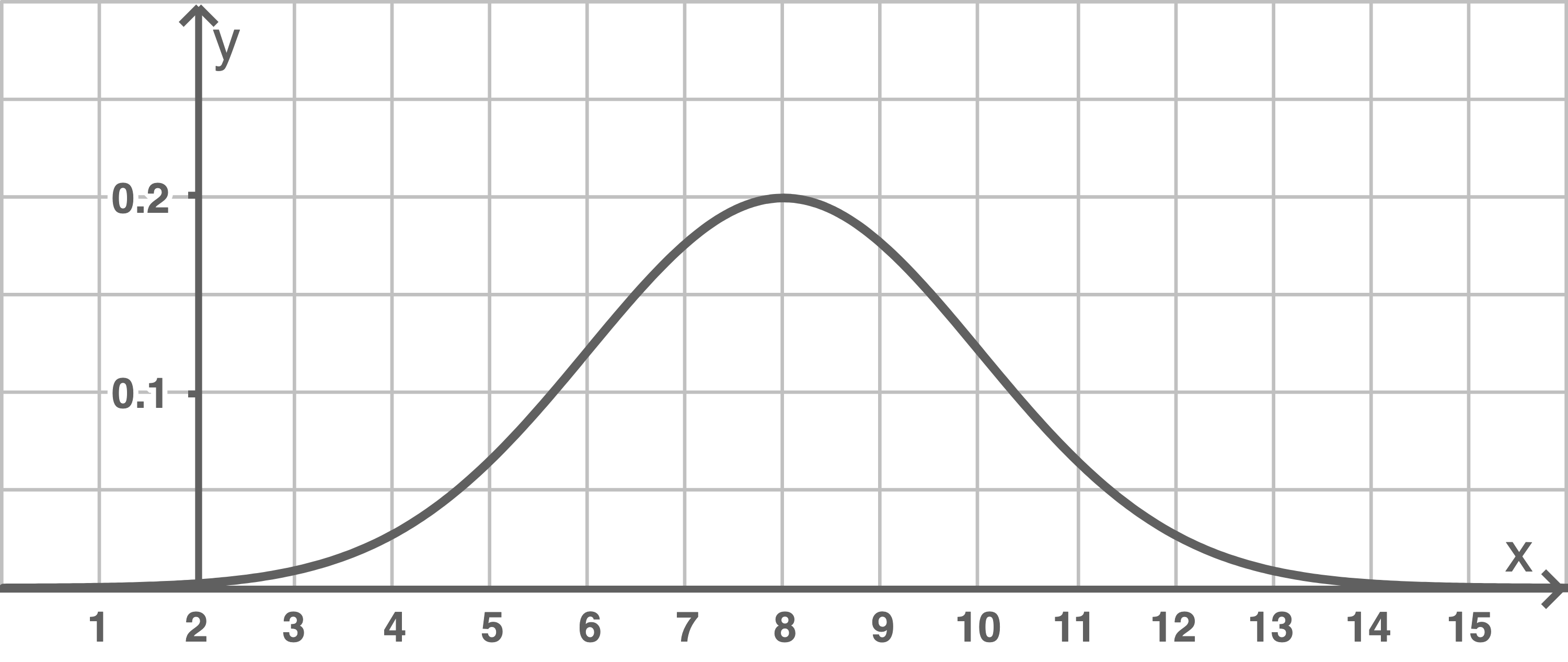
Eine Wahrscheinlichkeitsverteilung, die eine stetige Zufallsgröße beschreibt, ist die Normalverteilung. Diese hat die folgenden Eigenschaften:- Die Funktionsgleichung der Standard-Normalverteilung ist die Gaußsche Dichtefunktion mit
In diesem Fall ist der Erwartungswert
und die Standardabweichung
- Die sogenannte Glockenkurve für andere
und
ergibt sich durch Verschiebung des Graphen der Gaußschen Dichtefunktion um
-Achse, Streckung mit dem Faktor
in Richtung der
-Achse.
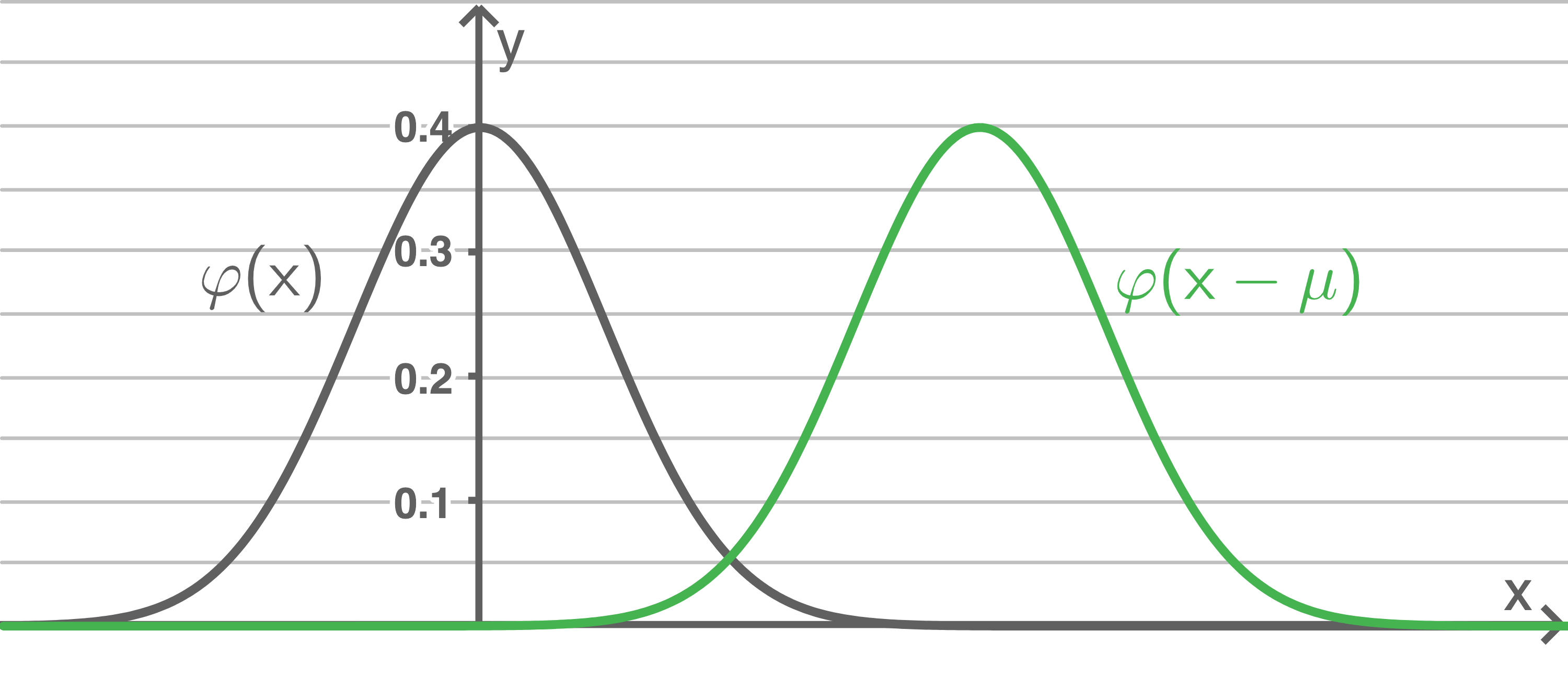
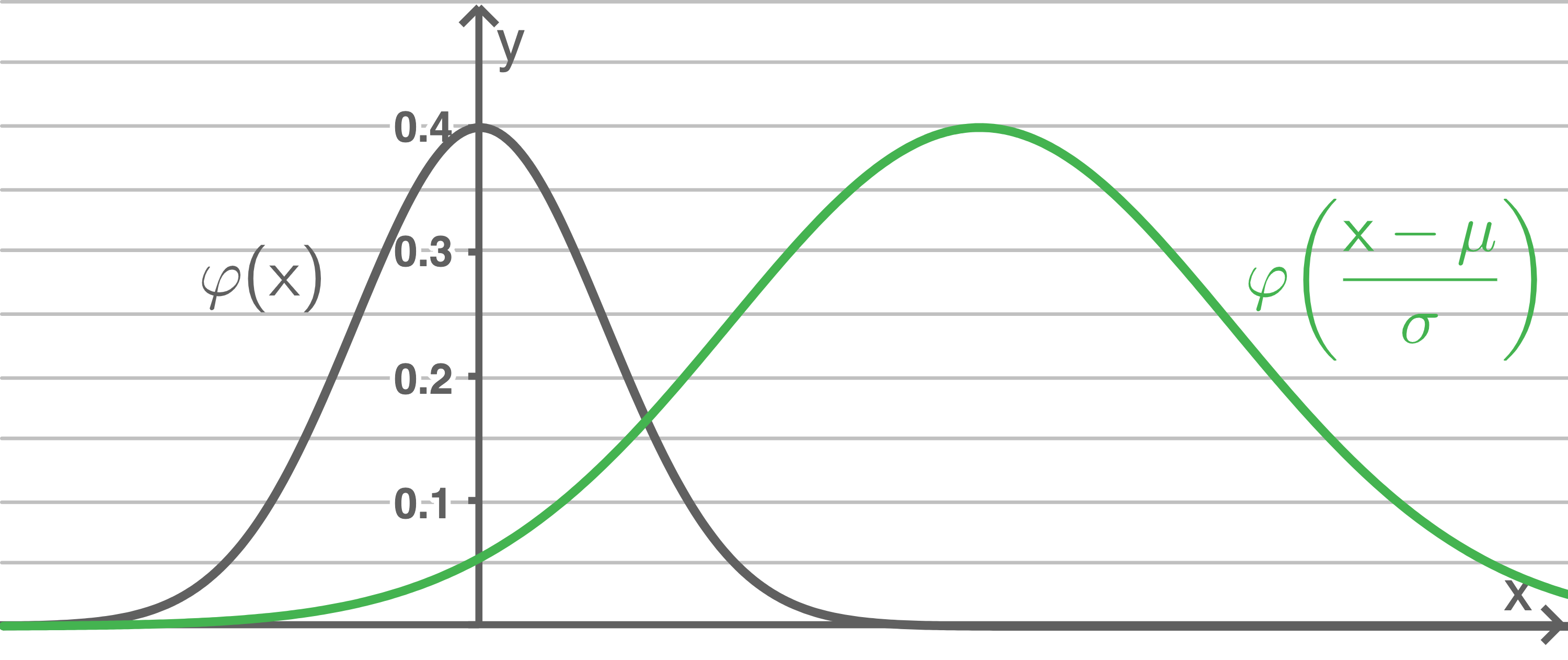
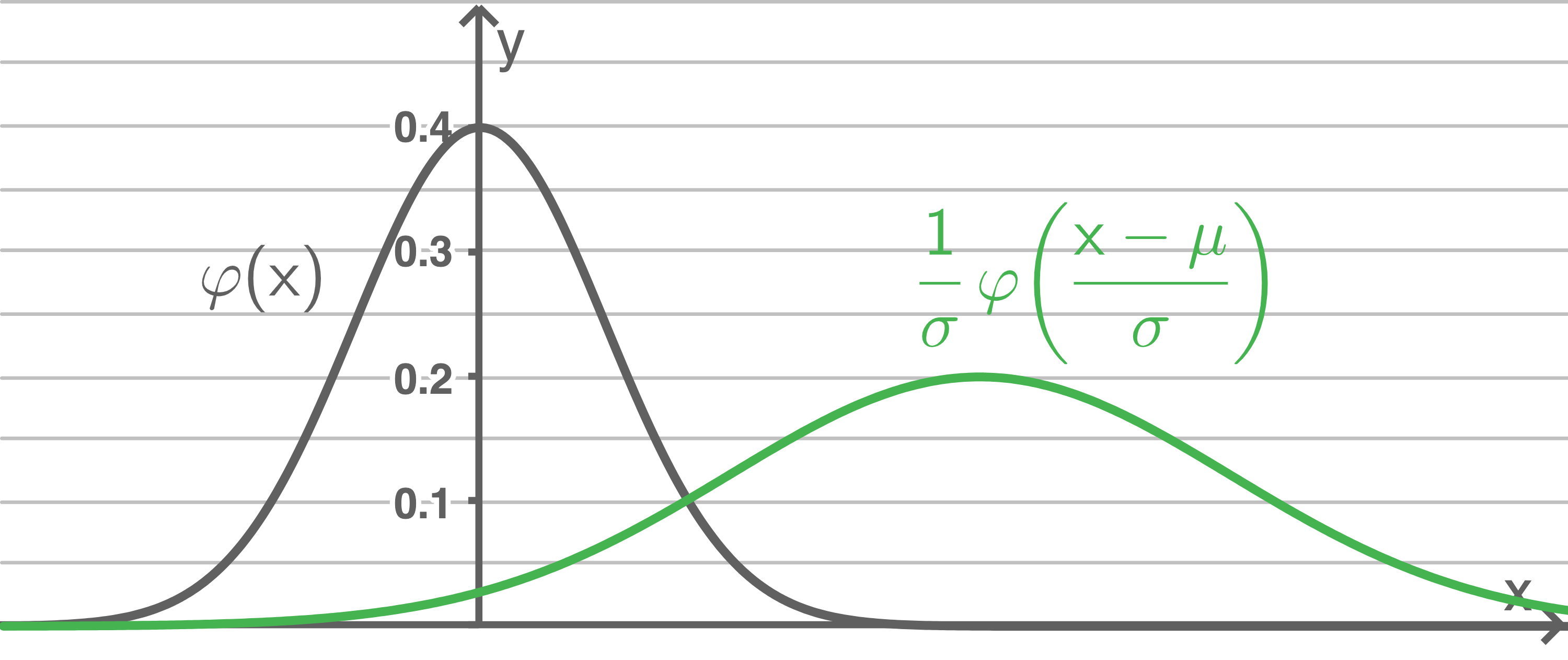
- Glockenkurven sind symmetrisch zum Erwartungwert
- Für normalverteilte Zufallsgrößen gilt:
- Bei großem Stichprobenumfang gilt für den arithmetischen Mittelwert:
- Bei großem Stichprobenumfang gilt für die empirische Standardabweichung:
1
Das Körpergewicht in der Bevölkerung kann näherungsweise als normalverteilt betrachtet werden. Für Männer in Europa zwischen 20 und 25 Jahren liegt der Mittelwert bei 
bei einer Standardabweichung von 
Triff eine Aussage über das Gewicht, die
a)
auf ungefähr zwei Drittel aller 20- bis 25-jährigen europäischen Männer zutrifft.
b)
auf ungefähr ein Sechstel aller 20- bis 25-jährigen europäischen Männer zutrifft.
2
Aus eine Schale Trauben wird die Masse der einzelnen Trauben ermittelt. Sie ist normalverteilt mit Erwartungswert 
und Standardabweichung 
Zeichne den Graphen der zugehörigen Dichtefunktion.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Es gilt:
![\(\begin{array}[t]{rll}
P(\mu-\sigma\leq X \leq \mu+\sigma)&\approx& 68\,\% \\[5pt]
P(80,5-8,5\leq X \leq 80,5+8,5) &\approx& 68\,\% \\[5pt]
P(72\leq X \leq 89) &\approx& 68\,\% \\[5pt]
\end{array}\)](https://mathjax.schullv.de/3b32539134af208497407927f73e4ec7956b1e15fe28f9ab8fe9667baf1663ba?color=5a5a5a)
Ungefähr zwei Drittel aller männlichen Europäer zwischen 20 und 25 Jahren wiegen zwischen 72 und 89 Kilogramm.
b)
Aus der Berechnung in Teilaufgabe a) und der Symmetrie der Glockenkurve um den Erwartungswert folgt, dass ungefähr ein Sechstel aller männlichen Europäer zwischen 20 und 25 Jahren mehr als 89 Kilogramm wiegen.
2
