Vektoren vervielfachen

Skalare Multiplikation

Die skalare Multiplikation eines Vektors beschreibt die Multiplikation eines Vektors mit einer reellen Zahl (Skalar). Ein Vektor $\overrightarrow{v}=\pmatrix{v_x\\v_y\\v_z}$ wird dabei koordinatenweise vervielfacht.

Der Vektor $r\cdot \overrightarrow{v}=r\cdot \pmatrix{v_x\\v_y\\v_z}=\pmatrix{r\cdot v_x\\r\cdot v_y\\r\cdot v_z}$ mit $r\in \mathbb R$ heißt das $\boldsymbol{r}$ -fache des Vektors $\overrightarrow{v}.$

Geometrische Bedeutung

Sind zwei Vektoren $\overrightarrow{u}\neq \overrightarrow{o}$ und $\overrightarrow{v}\neq \overrightarrow{o}$ Vielfache voneinander, so heißen sie parallel zueinander.

Mittelpunkt einer Strecke berechnen

Der Mittelpunkt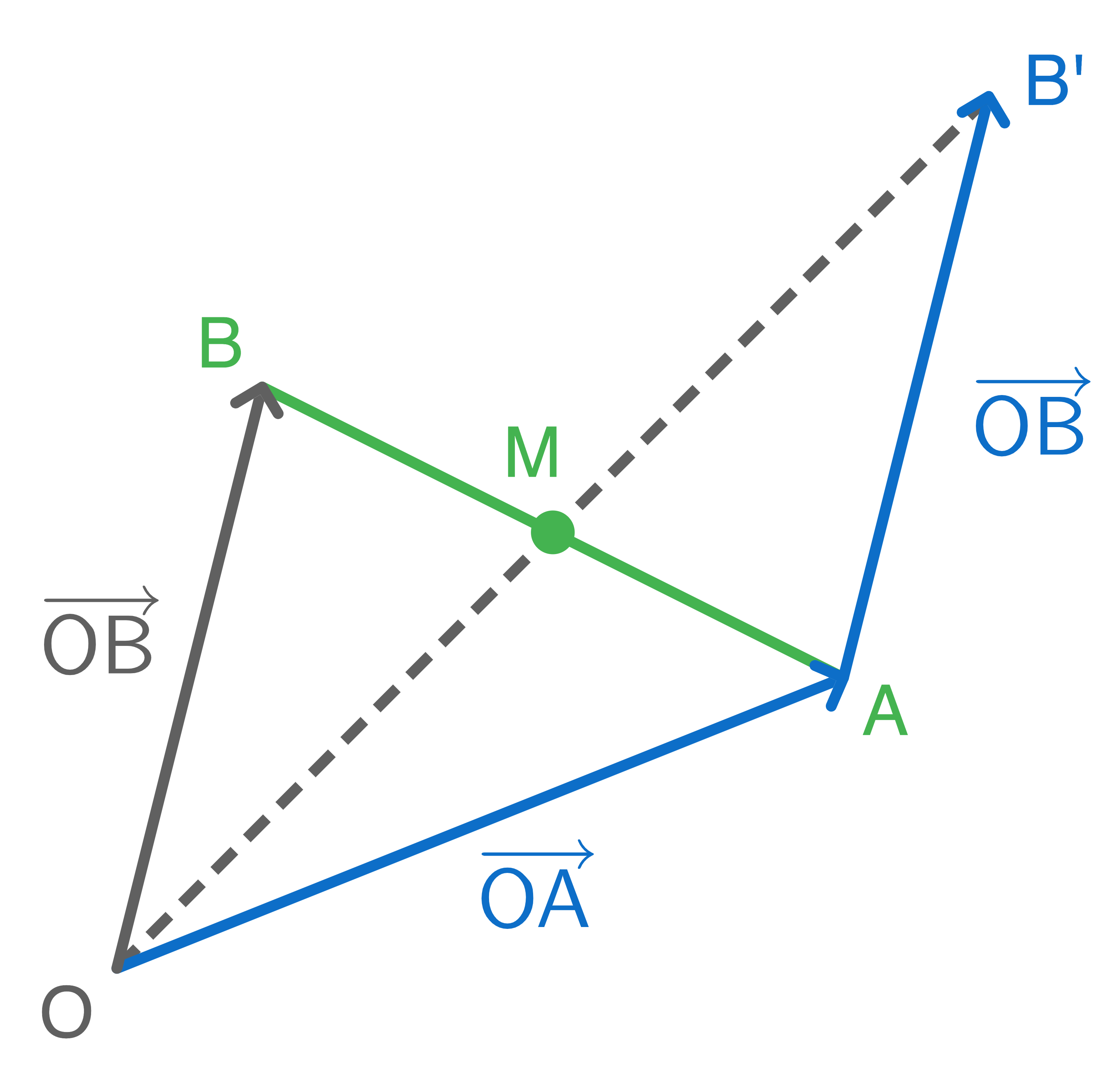 $M$ einer Strecke $\overline{AB}$ lässt sich wie folgt berechnen:

$\overrightarrow{OM}=\dfrac{1}{2}\cdot \left(\overrightarrow{OA}+\overrightarrow{OB}\right)$

mittelpunkt einer strecke berechnen, vektoren, skalare multiplikation, vektoren vervielfachen