Lerninhalte in Mathe

Digitales Schulbuch

Inhaltsverzeichnis

Sinus- und Kosinusfunktion

Die Funktion $f(x)=\sin(x)$ wird Sinusfunktion genannt.

Graph der Sinusfunktion:

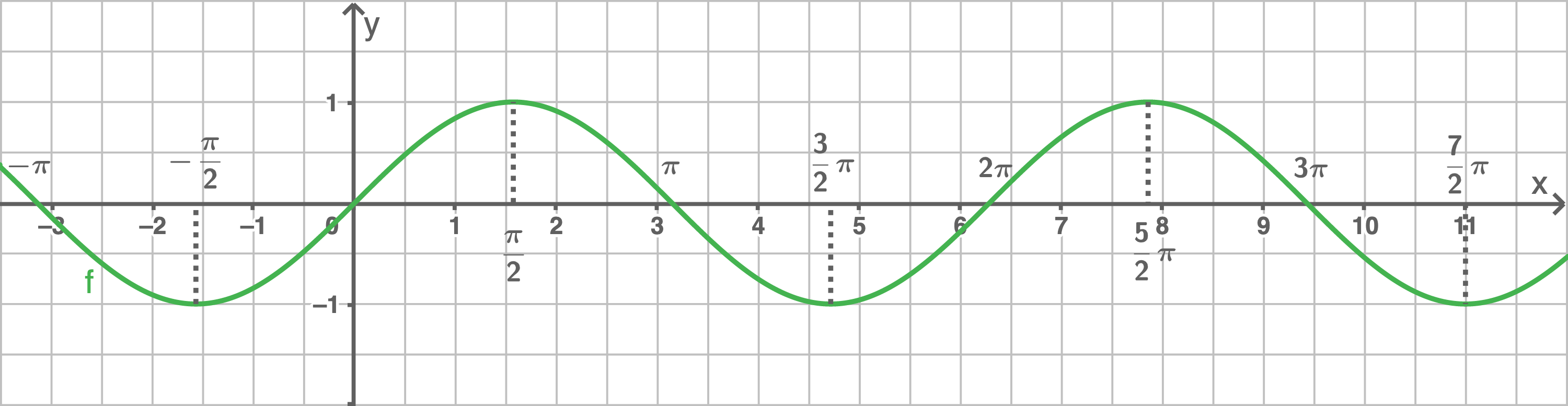Gymnasium Klasse 10 Sinus und Kosinus

Die Funktion $f(x)=\cos(x)$ wird Kosinusfunktion genannt.

Graph der Kosinusfunktion:

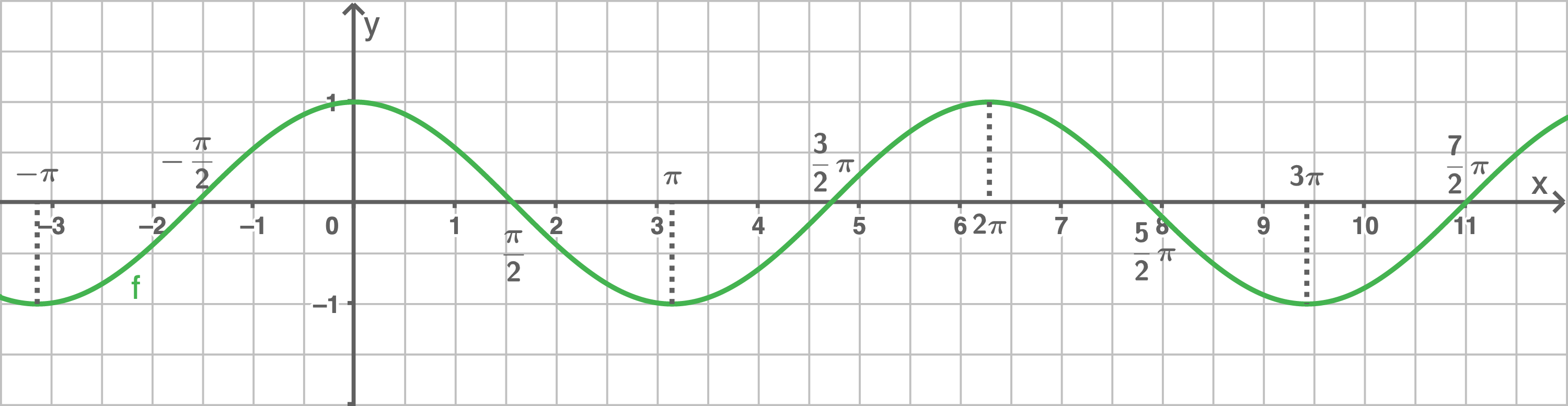
Gymnasium Klasse 10 Sinus und Kosinus

Eigenschaften

Sinus- und Kosinusfunktionen sind periodische Funktionen.

	$\color{#ffffff}{y=\sin(x)}$	$\color{#ffffff}{y=\cos(x)}$
Wertebereich	Wertebereich anzeigen $\{... \}$ Wertebereich für $y=\sin(x):$ $\{ y \in \mathbb{R} \mid -1 \leq y \leq 1 \}$	Wertebereich anzeigen $\{ ...\}$ Wertebereich für $y=\cos(x):$ $\{ y \in \mathbb{R} \mid -1 \leq y \leq 1 \}$
kleinste Periode	$2\pi$ $\sin(x+2\pi)$ $= \sin(x)$	$2\pi$ $\cos(x+2\pi)$ $= \cos(x)$
Symmetrie	punkt- symmetrisch zum Ursprung $\sin(-x)$ $=-\sin(x)$	achsen- symmetrisch zur $y$ -Achse $\cos(-x)= \cos(x)$
Nullstellen	$k\cdot \pi$ mit $k\in \mathbb{Z}$ $($ Nullstellen liegen bei ganzzahligen Vielfachen von $\pi)$	$k\cdot \pi$ $+ \frac{\pi}{2}$ mit $k\in \mathbb{Z}$ (Nullstellen liegen $\frac{\pi}{2}$ nach den ganzzahligen Vielfachen von $\pi)$

Extrempunkte von $\boldsymbol{y=\sin(x)}$ und $\boldsymbol{y=\cos(x)}$

Mittig zwischen zwei Nullstellen
Abwechslung von Hoch- und Tiefpunkten
Hochpunkte haben $y$ -Koordinate $1$
Tiefpunkte haben $y$ -Koordinate $-1$

Monotonie von $\boldsymbol{y=\sin(x)}$ und $\boldsymbol{y=\cos(x)}$

Graph ist fallend von Hochpunkt zum nächsten Tiefpunkt
Graph ist steigend von Tiefpunkt zum nächsten Hochpunkt