Symmetrie zur y-Achse und zum Ursprung
Der Graph einer Funktion 
ist
- achsensymmetrisch zur
-Achse, wenn gilt:
- punktsymmetrisch zum Ursprung, wenn gilt:
- achsensymmetrisch zur
- punktsymmetrisch zum Ursprung, wenn alle Exponenten (Hochzahlen) der Potenzen ungerade sind.
1
Ordne den Graphen die Funktionen zu und gib an, um welche Symmetrie der Graphen es sich handelt.
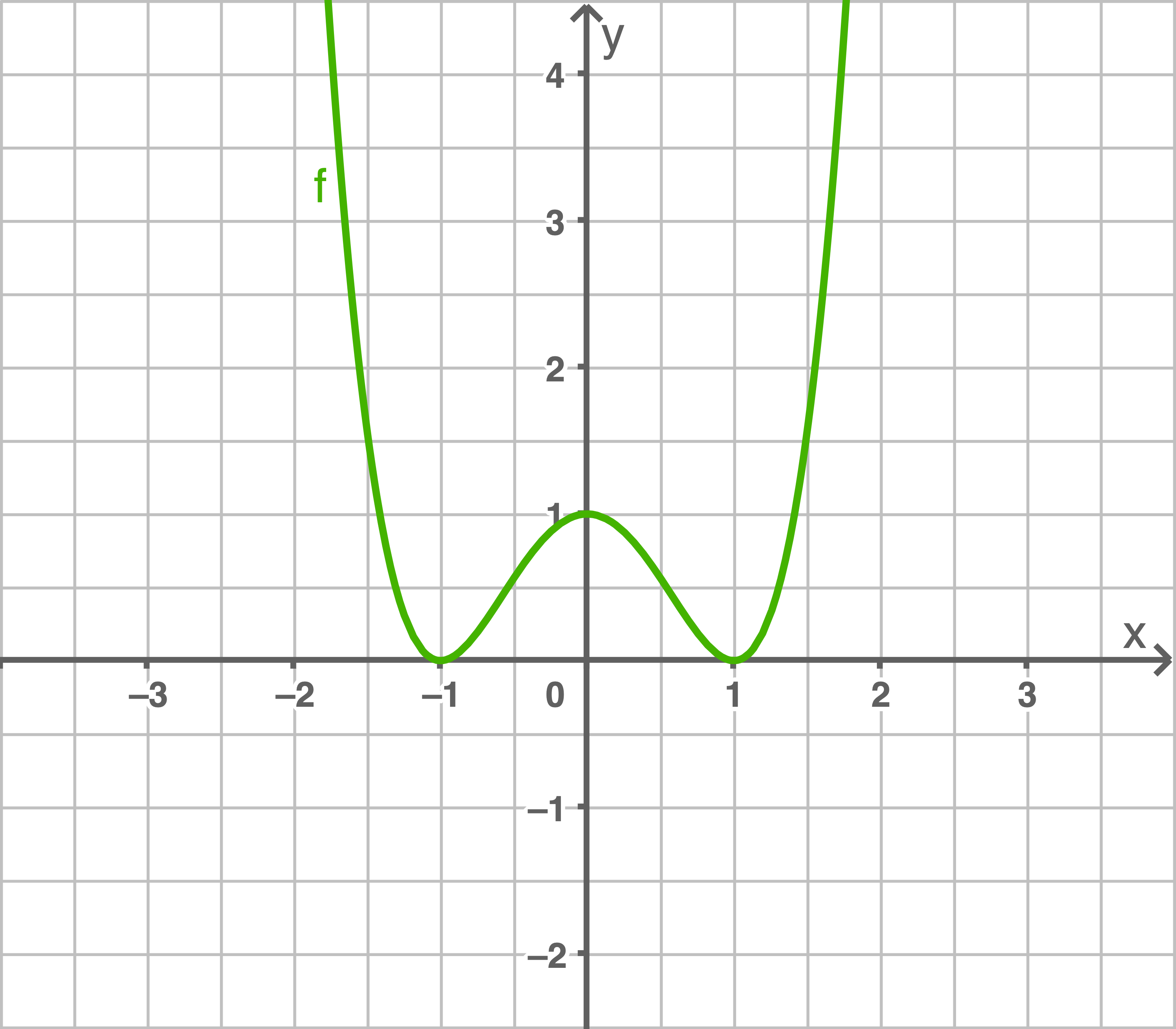
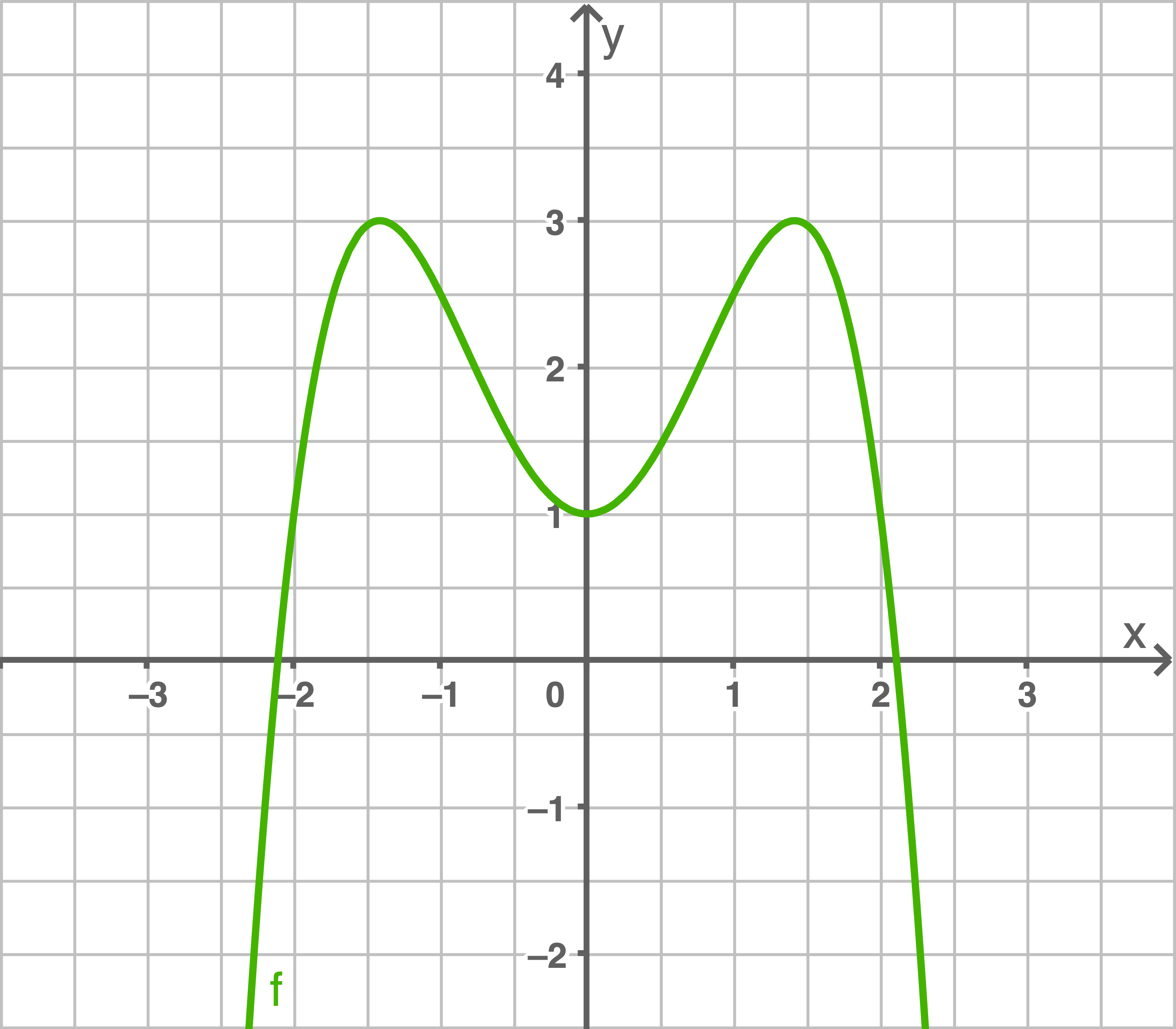
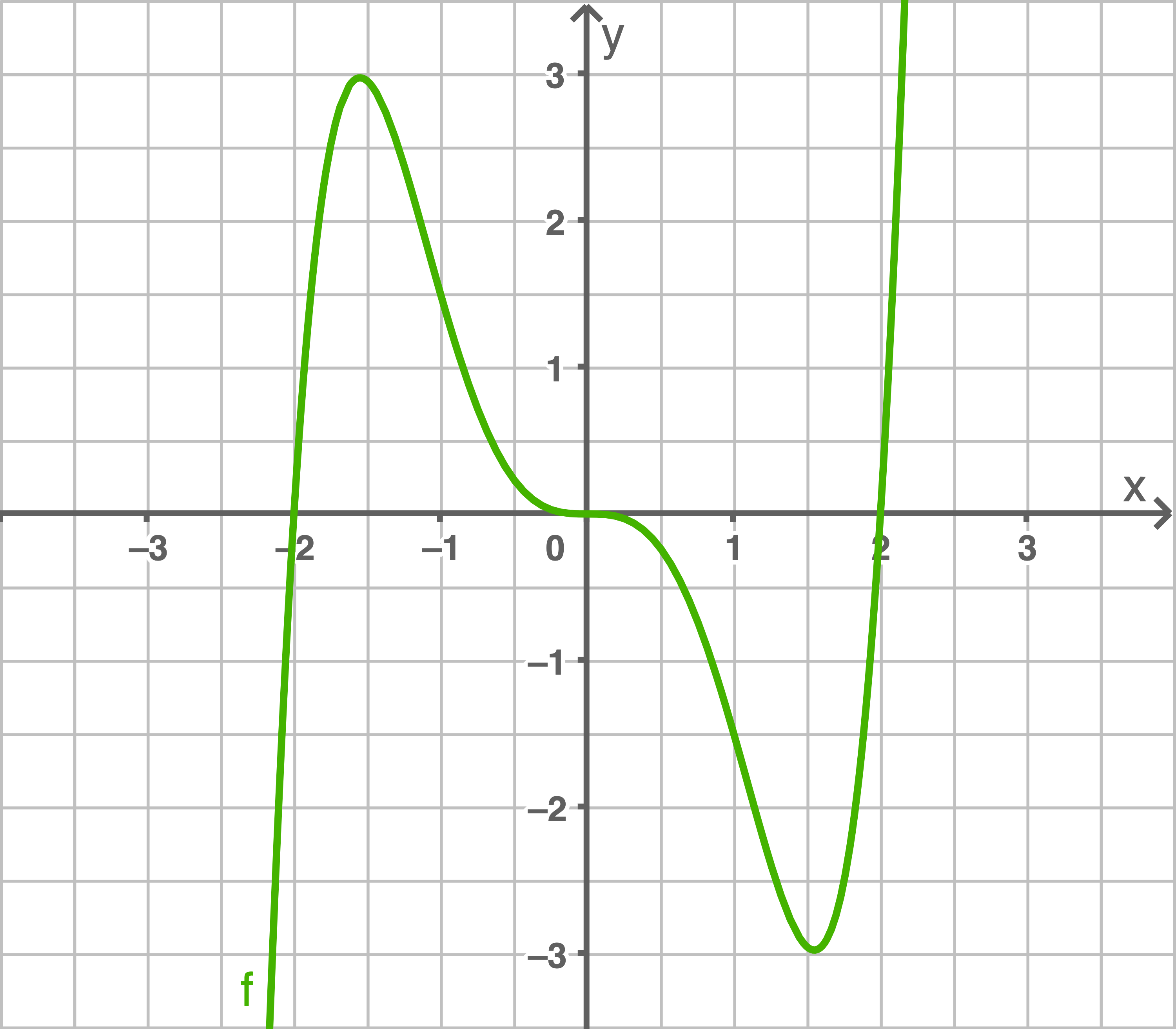
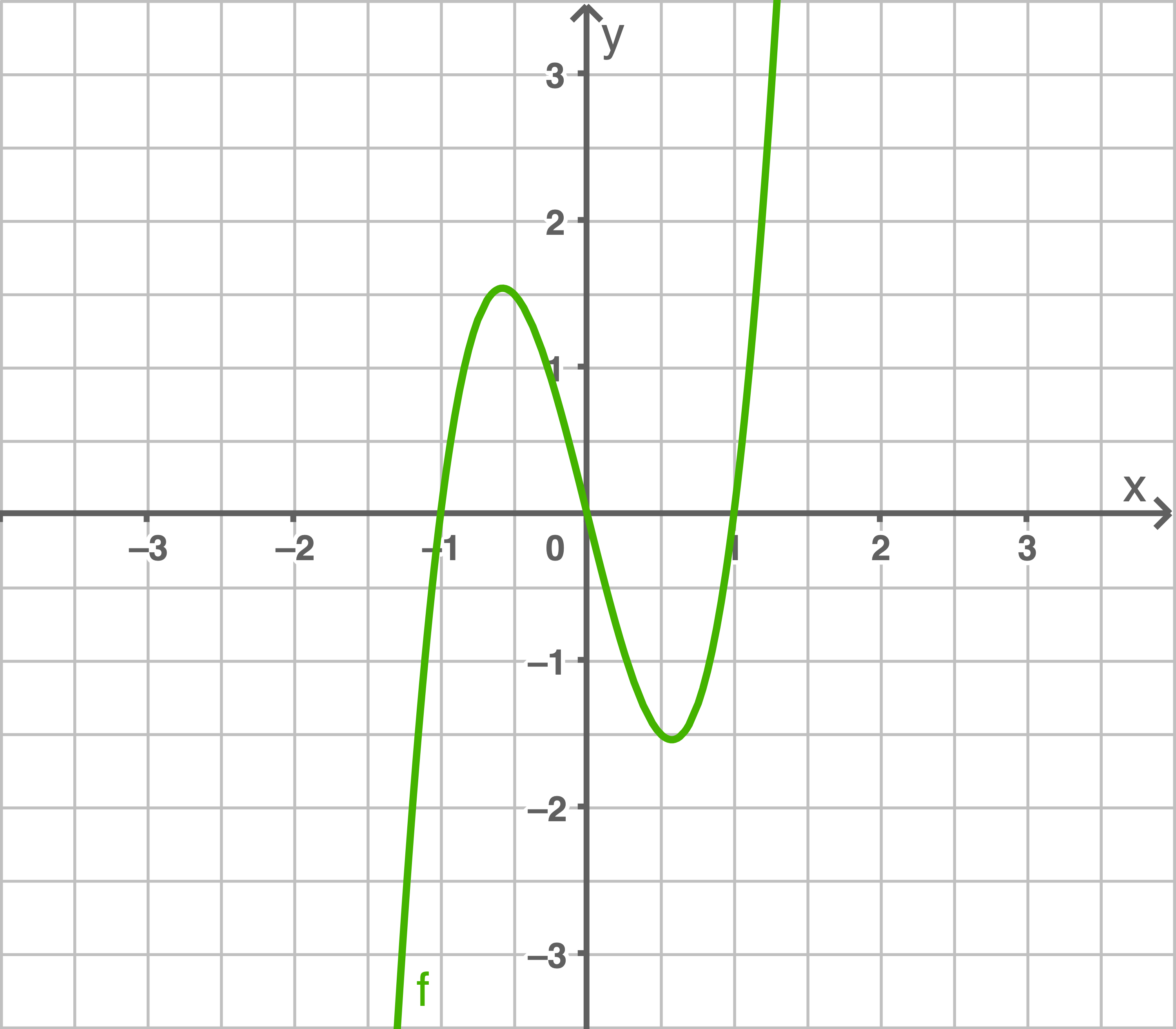
a)
b)
c)
d)
A.
B.
C.
D.
2
Was für eine Aussage zur Symmetrie des Graphen von kann getroffen werden?
a)
b)
c)
d)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Funktion C.
Achsensymmetrie zur 
-Achse
b)
Funktion A.
Achsensymmetrie zur -Achse
c)
Funktion D.
Punktsymmetrie zum Ursprung
d)
Funktion B.
Punktsymmetrie zum Ursprung
2
a)
Der Graph der Funktion ist weder achsensymmetrisch zur -Achse noch punktsymmetrisch zum Ursprung, da neben dem ungeraden Exponenten 3 auch der gerade Exponent 2 vorkommt.
b)
Der Graph der Funktion ist weder achsensymmetrisch zur -Achse noch punktsymmetrisch zum Ursprung, da sowohl ungerade als auch gerade Exponenten vorkommen (dabei ist 
c)
Der Graph der Funktion ist achsensymmetrisch zur -Achse, da nur geradzahlige Exponenten vorkommen (dabei ist 
d)
Der Graph der Funktion ist punktsymmetrisch zum Ursprung, da nur ungerade Exponenten vorkommen.