Wendestellen
Geht ein Graph einer Funktion von einer Linkskurve in eine Rechtskurve über oder umgekehrt, so liegt eine Wendestelle von 
vor.
gilt und die dritte Ableitung an dieser Stelle ungleich Null ist (
), dann liegt an der Stelle 
eine Wendestelle vor.
Nachweis mit Vorzeichenwechsel
Wenn für die zweite Ableitung gilt und die zweite Ableitung an dieser Stelle einen Vorzeichenwechsel hat, dann liegt an der Stelle eine Wendestelle vor.
mit 
Bestimme den Wendepunkt des Graphen von und begründe mit Hilfe der dritten Ableitung.
![\(\begin{array}[t]{rll}
6x-6&=&0 &\quad \scriptsize \mid\;+6 \\[5pt]
6x&=&6 &\quad \scriptsize \mid\;:6 \\[5pt]
x&=&1
\end{array}\)](https://mathjax.schullv.de/f6e93754cb39860d284336d16a9cb2550e88e7b93993a045c0f4b629e5e0dda9?color=5a5a5a)
in 
einsetzen:
in 
einsetzen:
mit Bestimme den Wendepunkt des Graphen von und begründe mit Hilfe des Vorzeichenwechsels.
für 
(Rechtskurve) und 
für 
(Linkskurve), also liegt ein Vorzeichenwechsel von 
an der Stelle 
vor.
in einsetzen:
Nachweis von Wendestellen
Nachweis mit dritter Ableitung Wenn für die zweite AbleitungBeispiel mit dritter Ableitung
Gegeben ist die FunktionBeispiel mit Vorzeichenwechsel
Gegeben ist die Funktion
1
Gib die Intervalle an, in denen der Graph von eine Rechtskurve bzw. eine Linkskurve ist.
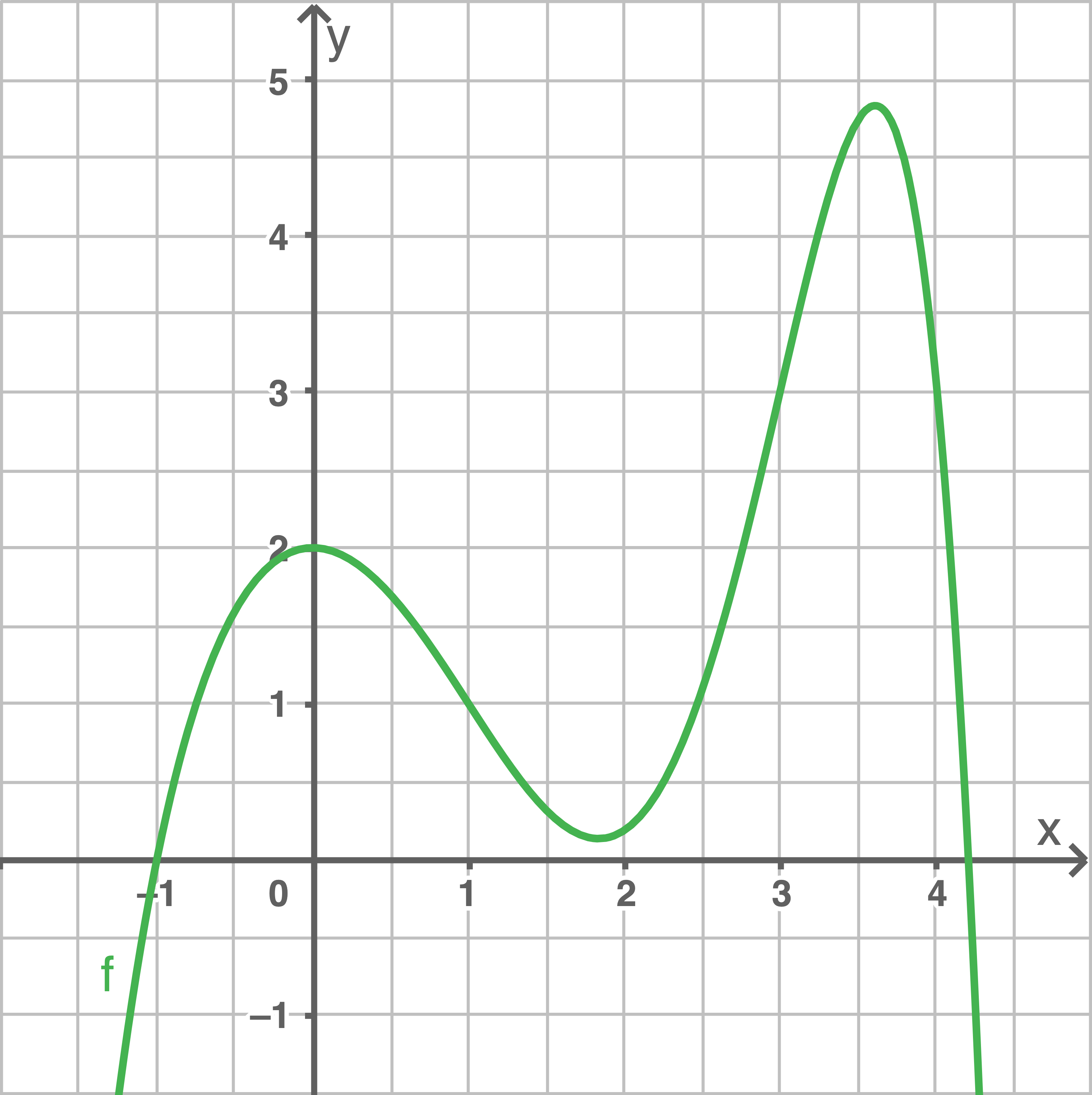
2
Berechne die Koordinaten der Wendepunkte des Graphen von mit Hilfe der dritten Ableitung.
a)
b)
c)
d)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
Rechtskurve: 
und 
Linkskurve: 
2
a)
b)
c)
d)